4 закона логики, которые помогут определить ложные суждения

В жизни мы часто слышим фразы «это не поддается логике» или «это нелогично». В целом мы понимаем, что речь идет про неверное суждение, ошибочные выводы. Но в чем конкретно нарушена логика — сказать трудно. Существуют 4 закона логики, с помощью которых можно легко отделить ложь от правды. Логика — это древняя наука, появившаяся в 4 веке до н.э., ее основателями были Аристотель, Сократ, Платон и многие другие известные философы, которые усердно изучали законы и формы правильного логического мышления. Давайте разберем на простых примерах значения основных четырех законов логики и как их применить в жизни.

Закон тождества

Любая мысль должна соответствовать самой себе, то есть иметь конкретное значение и быть точной и понятной. Самый известный пример: «ученики прослушали урок». Термин «прослушали» в этом предложение может иметь два определения: то ли ученики ничего не слушали на уроке, то ли, наоборот, внимательно изучали новую тему.

Главное, на что необходимо обращать внимание, так это на неоднозначные слова, которые могут иметь несколько значений. Сложнее всего распознать нарушение тождества в сложных утверждениях:

• Что вы выберите: счастье или конфету? — Счастье.
• Как вы считаете, что лучше счастья? —Ничто!
• Но конфета лучше, чем ничто.
• Поэтому конфета получается лучше счастья.

В примере понятие «ничто» в первом варианте означало «отказ от выбора варианта», во втором, как отсутствие чего-либо.

Пройдите онлайн-курсы бесплатно и откройте для себя новые возможности Начать изучение

Закон противоречия

Две отрицающих друг друга мысли не могут быть одинаково верными. Например, когда говорят «черный пес» и «белый пес», имея в виду одного и того же пса в одном промежутке времени, то правильным может быть только одно утверждение. В жизни важно выявлять противоречия, отделять игру слов от лжи.

Закон исключенного третьего

Два противоречащих утверждения не должны быть одинаково ложными. Тут важно отличать противоречащие от противоположных утверждений. Первые суждения не имеют третьего варианта, например, большая квартира и небольшая квартира. Противоположные суждения допускают, что возможен и другой вариант, например, «маленькая квартира» и «большая квартира», другой вариант — «средняя квартира». На простых примерах принцип понятен, а вот в жизни противоречащие суждения обычно разделены длинным предисловием, который сбивает с мысли.

Закон достаточного основания

Истинная мысль должна быть основана на аргументах, чтобы быть истинной. Важно, что само утверждение должно следовать из этих фактов. Например, «я готовился к экзамену, поэтому я не заслужил двойку». Один факт не подтверждает утверждение, студент мог просто прочесть лекции и не заучивать нужный материал. Данный закон помогает не делать преждевременных выводов и не верить, например, разной желтой прессе.

Проверьте себя прямо сейчас, как хорошо вы разбираетесь в логике, пройдите бесплатный онлайн-тест на логику.

Разбираем 4 закона логики Аристотеля с примерами для менеджеров! | Ядро психологии и переговоров!

Логика Аристотеля, кратко. Законы формальной логики, примеры. Закон тождества. Закон противоречия. Закон исключения третьего. Закон достаточного основания.

Здравствуйте, уважаемые читатели!

Меня зовут Влад Ядро! Мне 45 лет. Профессиональный переговорщик, тренер и консультант по переговорам. Клинический психолог. Построил карьеру в продажах с «0» до генерального директора крупного торгового оптового бизнеса. С 2014 г собственный консалтинговый бизнес в области переговоров. Звоните! Пишите! Я Вам помогу решить сложности в коммуникациях с другими людьми!

Сегодня следует продолжение цепочки статей, раскрывающих законы формальной логики.

№ 1. Статья «Понятие это в логике? Логика Аристотеля кратко и понятно!»

№ 2. Статья «Суждения это в логике? Сложные суждения примеры. Классификация.»

№ 3. Статья «Умозаключение в логике это? Дедуктивные умозаключения это?»

№ 4. Статья «Индуктивные умозаключения это? Умозаключения по аналогии, примеры.»

Источником для данной статьи послужила книга Гусев Д. А. «Краткий курс логики: Искусство правильного мышления».

Блок 1. Логика Аристотеля. Закон тождества.

Любое понятие, суждение, умозаключение должно быть тождественно, равно себе и не может означать другое, порождать другой смысл.

Формула: а → а (если «а», то «а») – тождественно-истинная.

Пример нарушения закона:

• Покажи нам, где ты нашел ключ!
• Там есть отличные груши!
• Света уже устала от этого брака.
• Убери резинку!
• Только некомпетентность менеджера может привести к такому плачевному результату.

Все это неясные, неопределенные высказывания. Ключ можно использовать в нескольких значениях: ключ от двери, ключ – источник родниковой воды, ключ – информационный шифр.  Груши можно понимать, как фрукты, или как спортивный боксерский снаряд, или как людей для битья.   Брак, как форма отношений или некачественное изделие. Резинка может быть жевательная, канцелярская, гимнастическая, сантехническая, или указывать на изделие. Некомпетентность менеджера в чем проявляется? Как понимать плачевный результат?

Что такое софизм?

Намеренное нарушение логических законов с целью запутать слушателей и зафиксировать вывод в качестве истины, используя условно правильную аргументацию.

Пример софизма № 1:

• Какие клиенты наиболее ценные для нас: лояльные или с просроченной дебиторской задолженностью?
• Безусловно, лояльные и Вы с этим согласитесь!
• А какие клиенты могут быть лучше лояльных?
• Это партнеры, с которыми мы пока еще не работаем, потому что они принесут дополнительную прибыль и размер ее будет больше!
• Но давайте смотреть правде в глаза, ведь клиенты с ПДЗ полезнее для нас, чем потенциальные партнеры, потому что мы уже заработали и продолжаем зарабатываем прибыль, работая с ними!
• Следовательно, на самом деле, наши клиенты с ПДЗ лучше многих лояльных клиентов!

Пример софизма № 2:

• Федор, ты согласен с тем, что если у тебя забрали каких-то клиентов, то у тебя их сейчас нет?
• Да, согласен.
• Федор, соответственно те клиенты, которых у тебя не забрали,  сейчас работают с тобой, здесь у тебя не будет возражений?
• Нет, не будет.
• Федор, у тебя ведь не забирали двух клиентов «А» и «В»?
• Нет, не забирали.
• Значит ты работаешь с этими клиентами тайно от нас, ведь ты же сам признал, что клиенты, которых у тебя не забрали, отгружаются тобой. А раз так, то твой план продаж будет на 10% выше!

Примеры нарушений закона (анекдоты):

• Хочу вот купить собаку, жена не дает. Думаешь собака даст?
• Летописец это не тот, кто пишет историю, летописец — это плохое лето.
• Вы знаете убийцу Пушкина А.С.? Конечно, но ведь он вроде не убийца, а великий поэт.

СМОТРИТЕ ВИДЕО «Переговоры с покупателем. Переговоры по задолженности. Возврат долга с юридического лица?!»

Блок 2. Логика Аристотеля. Закон противоречия.

Два суждения не могут быть одновременно истинными, если в отношении одного предмета при прочих равных условиях присутствует утверждение с одной стороны и отрицание, с другой стороны.

Пример:

• Федор – это менеджер отдела продаж компании «Х» на 01.05.2019.
• Федор – это не менеджер отдела продаж компании «Х» на 01.05.2019.

Формула: ¬ (а ˄ ¬ а) неверно, что «а» и не «а» (суждение).

Противоречия отражают нарушения этого закона. Различают:

• Контактное противоречие. Последующее суждение отрицает предыдущее суждение без интервала в тексте или речи. Пример: высказывание в 32 главе книги противоречит суждению в 32 главе книги. Подобные противоречия редко можно наблюдать.
• Дистантное противоречие. Последующее суждение отрицает предыдущее суждение с интервалом в тексте или речи. Пример: высказывание в 32 главе книги противоречит суждению в 15 главе книги. Подобные противоречия часто можно наблюдать.
• Явное противоречие.  Последующее суждение непосредственно противоречит предыдущему суждению.
• Неявное противоречие. Последующее суждение опосредованно противоречит предыдущему суждению.

4 вида комбинированных противоречий.

1. Контактные явные. Пример:

• Федор позвонил и сообщил, что задержится в дороге из-за пробок, но не согласовал это с руководством.
• А вот и наши «звезды», которые уже совсем и не «звезды»!

2. Контактные неявные. Пример:

• Первые отгрузки у нас состоялись уже в середине мая (открытие ООО произошло 21 мая).
• Федор выполнил план продаж в 1 квартале на 98%, поэтому бонусы не заработал (в марте не было товара на складе компании и Федор не мог выполнить план на 100%).

3. Дистантное явное. Пример:

• У нас был выбор, какой смартфон купить, учитывая большой ассортимент магазина.
• По сути у нас не было выбора, только эта модель смартфона подходила по всем параметрам.

4. Дистантное неявное. Пример:

• Отдел продаж был сформирован сразу вместе с отделами логистики и закупок, когда открылась компания (сказал спикер на конференции в начале своей презентация).
• На начальном этапе нашей деятельности мы все были продавцами (в конце беседы, когда спикер отвечал на вопросы аудитории).

Блок 3. Логика Аристотеля. Закон исключения третьего.

Два противоречащих суждения не могут быть одновременно истинными или ложными  об одном и том же предмете при прочих равных условиях, если истинно первое, то второе ложное, верно и наоборот.

Формула: а ˅ ¬ а («а» или не «а»).

Что такое противоположные суждения?

Это суждения, между которыми возможен третий, промежуточный вариант. Пример:

• Анна отлично играет в теннис.
• Анна плохо играет в теннис.
• Анна удовлетворительно играет в теннис (промежуточный вариант).

Противоположные суждения могут быть одновременно ложными, но не могут быть одновременно истинными.

Что такое противоречащие суждения?

Это суждения, между которым не может быть промежуточных вариантов. Пример:

• Анна умеет играть в теннис.
• Анна не умеет играть в теннис.

Здесь невозможен промежуточный вариант. Противоречащие суждения не могут быть одновременно истинными или одновременно ложными.

Заказать тренинг «Переговоры — Партнерство»

Блок 4. Логика Аристотеля. Закон достаточного основания.

Любое высказывание имеют силу только в случае обоснования свидетельствами, достаточными для его доказательства, тезис должен следовать из оснований с необходимостью.

Примеры:

• Федор заключает сделки с клиентами (суждение), потому что он работает в отделе продаж компании (основание).

Примеры нарушений:

• Анна заключает сделки с клиентами (суждение), потому что в компании есть отдел продаж (основание).

Из основания « в компании есть отдел продаж» вовсе не следует, что «Анна заключает сделки с клиентами».

• На этом участке дороги скоростной режим ограничен (тезис), потому что идут строительные работы (основание).

Строительные работы могут идти или не идти, это не связано с ограничением скорости. Скорость автомобилей может быть ограничена только при наличии соответствующих законов, дорожных знаков или данных из инструкции по эксплуатации транспортного средства.

• Гражданина «А» признают  виновным в том, что он нанес повреждения автомобилю гражданина «В».  В основание обвинения легли свидетельские показания некого гражданина «Х».

Свидетельские показания гражданина «Х» не являются достаточными основаниями для вынесения обвинительного приговора, соответственно приговор обязательно надо обжаловать ответчику.

• Сергей в 2019 г работает по своей специальности.
• В 2018 г Сергей закончил медицинский университет по специальности «врач-психиатр».
• Соответственно, Сергей в 2019 г работает врачом-психиатром. 

Кем работает Сергей в 2019 г не вытекает с необходимостью из двух посылок. Сергей мог получить еще одну специальность раньше, например, инженера сетевого оборудования и работать в 2019 г инженером.

• Мы раньше уже запускали рекламу в интернете, потратили на это 1 млн руб, но выручка у нас не выросла, а чистая прибыль даже сократилась.
• Поэтому мы скептически относимся к рекламе в интернете и больше не будем на это тратить свои деньги.

Тот факт, что когда-то компания потратила безрезультатно деньги в определенной ситуации не означает с необходимостью истинное положение дел для всех ситуаций с рекламой в интернете или других гипотетических вариантов. «Случайные истины» не релевантны для общих или иных отдельных ситуаций. Подобные умозаключения менеджеров говорят о непонимании истинных причин полученных негативных результатов и проявленной интеллектуальной лени или тупости в поиске подлинных причин.

• Наша компания увеличивает выручку из года в год в среднем на 10%, что говорит о правильной стратегии и грамотных тактических шагах высшего руководства!

Рост выручки не вытекает с необходимость из стратегии и тактики высшего руководства, а связан с уровнем инфляции. Можно годами ничего вообще не менять в компании и при этом увеличивать выручку, элементарно за счет увеличения стоимости закупаемой и соответственно продаваемой продукции, при этом коэффициент рентабельности также остается без изменений.

• Правительство не решает проблемы населения на протяжении всех 5 лет, потому что в его составе нет тех, кто искренне заинтересован в народе; кроме своего кармана, их вообще ничто не интересует!

Этот популистский лозунг явно демонстрирует нарушение закона достаточного основания. Во-первых, в составе правительства могут быть люди, искренне заинтересованные в народе, поэтому нельзя делать вывод «плохое правительство – значит плохие все члены правительства». Во-вторых, сведение всех мотивов лишь к одному («забота о кармане») вовсе не исключает решения проблем населения. В-третьих, не решение проблем населения не подразумевает присутствие только одной причины и причины только такого содержания.

• Сборная этой страны выиграет чемпионат мира по футболу, ведь у нее «звездный состав», поэтому сделаю на нее ставку.

Как Вы понимаете «звезды» тоже люди и делать ставку с опорой только на этот компонент — глупость. Здесь также нарушен закон достаточного основания.

На сегодня это все! Думайте правильно! Изучайте теорию!

УМНЫЕ КНИГИ по современной поведенческой психологии, теории принятия решений, когнитивным иллюзиям, мотивации, лидерству, саморазвитию, ошибкам в мышлении Вы можете БЕСПЛАТНО скачать с моего сайта здесь: https://yakimovvlad.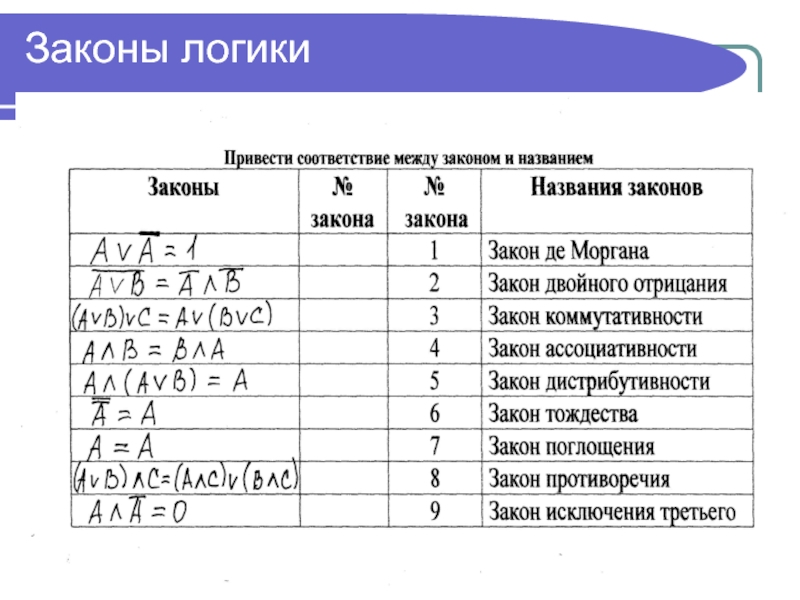 ru/knigi-psixologiya

Друзья, ставьте лайки, от этого становится позитивно не только мне, но и Вам, потому что это Ваш поступок, это Вы добавили улыбок в наш мир! И пишите свои комментарии, высказывайтесь и Ваше мнение услышат тысячи людей!

Пожалуйста делитесь в социальных сетях этой статьей, помогите мне распространять знания БЕСПЛАТНО, ведь кому-то это может помочь в жизни справиться со сложной ситуацией! Спасибо, Вам!

Спасибо за Ваше внимание! С Вами был Ядро Владислав, тренер по переговорам! До встречи и пока!

Закон тождества и другие важнейшие законы логики

Автор: Дмитрий Алексеевич Гyceв, кандидат философских наук, доцент кафедры философии Московского педагогического государственного университета.

 

Первый и наиболее важный закон логики — это закон тождества, который был сформулирован Аристотелем в трактате «Метафизика» следующим образом: «…иметь не одно значение — значит не иметь ни одного значения; если же у слов нет значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности — и с самим собой; ибо невозможно ничего мыслить, если не мыслить что-нибудь одно». Можно было бы добавить к этим словам Аристотеля известное утверждение о том, что мыслить (говорить) обо всем — значит не мыслить (не говорить) ни о чем.

Закон тождества утверждает, что любая мысль (любое рассуждение) обязательно должна быть равна (тождественна) самой себе, т. е. она должна быть ясной, точной, простой, определенной. Говоря иначе, этот закон запрещает путать и подменять понятия в рассуждении (т.е. употреблять одно и то же слово в разных значениях или вкладывать одно и то же значение в разные слова), создавать двусмысленность, уклоняться от темы и т.п.

Например, непонятен смысл фразы: «Из-за рассеянности на турнирах шахматист неоднократно терял очки». Очевидно, что по причине нарушения закона тождества появляются неясные высказывания (суждения). Символическая запись этого закона выглядит так: а → а (читается: «Если а, то а»), где а — это любое понятие, высказывание или целое рассуждение.

Когда закон тождества нарушается непроизвольно, по незнанию, тогда возникают просто логические ошибки; но когда этот закон нарушается преднамеренно, с целью запутать собеседника и доказать ему какую-нибудь ложную мысль, тогда появляются не просто ошибки, а софизмы.

Таким образом, софизм — это внешне правильное доказательство ложной мысли с помощью преднамеренного нарушения логических законов.

Приведем пример софизма: «Что лучше: вечное блаженство или бутерброд? Конечно же, вечное блаженство. А что может быть лучше вечного блаженства? Конечно же, ничто! Но бутерброд ведь лучше, чем ничто, следовательно, он лучше вечного блаженства». Попробуйте самостоятельно найти подвох в этом рассуждении, определить, где и как в нем нарушается закон тождества и разоблачить этот софизм.

Вот еще один софизм: «Спросим нашего собеседника: «Согласен ли ты с тем, что если ты что-то потерял, то у тебя этого нет?» Он отвечает: «Согласен». Зададим ему второй вопрос: «А согласен ли ты с тем, что если ты что-то не терял, то у тебя это есть?» — «Согласен», — отвечает он. Теперь зададим ему последний и главный вопрос: «Ты не терял сегодня рога?» Что ему остается ответить? «Не терял», — говорит он. «Следовательно, — торжествующе произносим мы, — они у тебя есть, ведь ты же сам вначале признал, что если ты что-то не терял, то оно у тебя есть».

Попробуйте разоблачить и этот софизм, определить, где и как в данном внешне правильном рассуждении нарушается закон тождества.

Однако на нарушениях закона тождества строятся не только неясные суждения и софизмы. С помощью нарушения этого закона можно создать какой-нибудь комический эффект. Например, Николай Bacильeвич Гоголь в поэме «Мертвые души», описывая помещика Ноздрева, говорит, что тот был «историческим человеком», потому что где бы он ни появлялся, с ним обязательно случалась какая-нибудь «история». На нарушении закона тождества построены многие комические афоризмы. Например: «Не стой где попало, а то еще попадет». Также с помощью нарушения этого закона создаются многие анекдоты. Например:

– Я сломал руку в двух местах.
– Больше не попадай в эти места.

Как видим, во всех приведенных примерах используется один и тот же прием: в одинаковых словах смешиваются различные значения, ситуации, темы, одна из которых не равна другой, т. е. нарушается закон тождества.

Нарушение этого закона также лежит в основе многих известных нам с детства задач и головоломок. Например, мы спрашиваем собеседника: «За чем (зачем) находится вода в стеклянном стакане?» — преднамеренно создавая двусмысленность в этом вопросе (зачем — для чего и за чем — за каким предметом, где). Собеседник отвечает на один вопрос, например он говорит: «Чтобы пить, поливать цветы», а мы подразумеваем другой вопрос и, соответственно, другой ответ: «За стеклом».

В основе всех фокусов также лежит нарушение закона тождества. Эффект любого фокуса заключается в том, что фокусник делает что-то одно, а зрители думают совершенно другое, т. е. то, что делает фокусник, не равно (не тождественно) тому, что думают зрители, отчего и кажется, что фокусник совершает что-то необычное и загадочное. При раскрытии фокуса нас, как правило, посещает недоумение и досада: это было так просто, как же мы вовремя этого не заметили.

Закон противоречия говорит о том, что если одно суждение что-то утверждает, а другое то же самое отрицает об одном и том же объекте, в одно и то же время и в одном и том же отношении, то они не могут быть одновременно истинными.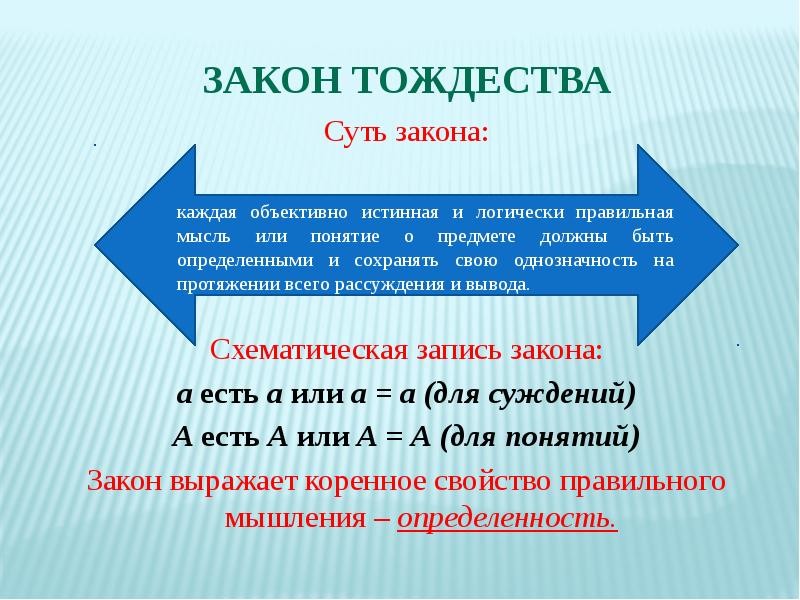 Например, два суждения: «Сократ высокий», «Сократ низкий» (одно из них нечто утверждает, а другое то же самое отрицает, ведь высокий — это не низкий, и наоборот), — не могут быть одновременно истинными, если речь идет об одном и том же Сократе, в одно и то же время его жизни и в одном и том же отношении, т. е. если Сократ по росту сравнивается не с разными людьми одновременно, а с одним человеком.

Понятно, что когда речь идет о двух разных Сократах или об одном Сократе, но в разное время его жизни, например в 10 лет и в 20 лет, или один и тот же Сократ и в одно и то же время его жизни рассматривается в разных отношениях, например он сравнивается одновременно с высоким Платоном и низким Аристотелем, тогда два противоположных суждения вполне могут быть одновременно истинными, и закон противоречия при этом не нарушается. Символически он выражается следующей тождественно-истинной формулой: ¬ (а Λ ¬ а), (читается: «Неверно, что а и не а»), где а — это какое-либо высказывание.

Говоря иначе, логический закон противоречия запрещает что-либо утверждать и то же самое отрицать одновременно. Но неужели кто-то станет нечто утверждать и то же самое тут же отрицать? Неужели кто-то будет всерьез доказывать, например, что один и тот же человек в одно и то же время и в одном и том же отношении является и высоким, и низким или что он одновременно и толстый, и тонкий; и блондин, и брюнет и т. п.? Конечно же нет. Если принцип непротиворечивости мышления столь прост и очевиден, то стоит ли называть его логическим законом и вообще уделять ему внимание?

Дело в том, что противоречия бывают контактными, когда одно и то же утверждается и сразу же отрицается (последующая фраза отрицает предыдущую в речи, или последующее предложение отрицает предыдущее в тексте) и дистантными, когда между противоречащими друг другу суждениями находится значительный интервал в речи или в тексте.

Например, в начале своего выступления лектор может выдвинуть одну идею, а в конце высказать мысль, противоречащую ей; так же и в книге в одном параграфе может утверждаться то, что отрицается в другом. Понятно, что контактные противоречия, будучи слишком заметными, почти не встречаются в мышлении и речи. Иначе обстоит дело с дистантными противоречиями: будучи неочевидными и не очень заметными, они часто проходят мимо зрительного или мысленного взора, непроизвольно пропускаются, и поэтому их часто можно встретить в интеллектуально-речевой практике.

Так, Bитaлий Ивaнoвич Свинцов приводит пример из одного учебного пособия, в котором с интервалом в несколько страниц сначала утверждалось: «В первый период творчества Маяковский ничем не отличался от футуристов», а затем: «Уже с самого начала своего творчества Маяковский обладал качествами, которые существенно отличали его от представителей футуризма».

Противоречия также бывают явными и неявными. В первом случае одна мысль непосредственно противоречит другой, а во втором случае противоречие вытекает из контекста: оно не сформулировано, но подразумевается. Например, в учебнике «Концепции современного естествознания» (этот предмет сейчас изучается во всех вузах) из главы, посвященной теории относительности Aльбeрта Эйнштейна, следует, что, по современным научным представлениям, пространство, время и материя не существуют друг без друга: без одного нет другого. А в главе, рассказывающей о происхождении Вселенной, говорится о том, что она появилась примерно 20 млрд. лет назад в результате Большого взрыва, во время которого родилась материя, заполнившая собой все пространство.

Из этого высказывания следует, что пространство существовало до появления материи, хотя в предыдущей главе речь шла о том, что пространство не может существовать без материи. Явные противоречия, так же как и контактные, встречаются редко. Неявные противоречия, как и дистантные, наоборот, в силу своей незаметности намного более распространены в мышлении и речи.

Примером контактного и явного противоречия может служить такое высказывание: «Водитель Н. при выезде со стоянки грубо нарушил правила, т. к. он не взял устного разрешения в письменной форме». Еще пример контактного и явного противоречия: «Молодая девушка преклонных лет с коротким ежиком темных вьющихся белокурых волос изящной походкой гимнастки, прихрамывая, вышла на сцену». Подобного рода противоречия настолько очевидны, что могут использоваться только для создания каких-нибудь комических эффектов.Поэтому наша задача — уметь их распознавать и устранять. Пример контактного и неявного противоречия: «Эта выполненная на бумаге рукопись создана в Древней Руси в XI в. (в XI в. на Руси еще не было бумаги)».

Наконец, наверное каждому из нас знакома ситуация, когда мы говорим своему собеседнику, или он говорит нам: «Ты сам себе противоречишь». Как правило, в этом случае речь идет о дистантных или неявных противоречиях, которые, как мы увидели, довольно часто встречаются в различных сферах мышления и жизни. Поэтому простой и даже примитивный, на первый взгляд, принцип непротиворечивости мышления имеет статус важного логического закона.

Важно отметить, что противоречия также бывают мнимыми. Некая мыслительная или речевая конструкция может быть построена так, что, на первый взгляд, выглядит противоречивой, хотя на самом деле никакого противоречия в себе не содержит. Например, известное высказывание Антона Пaвлoвича Чехова: «В детстве у меня не было детства», — кажется противоречивым, т. к. оно вроде бы подразумевает одновременную истинность двух суждений, одно из которых отрицает другое: «У меня было детство», «У меня не было детства».

Таким образом, можно предположить, что противоречие в данном высказывании не просто присутствует, но и является наиболее грубым — контактным и явным. На самом же деле никакого противоречия в чеховской фразе нет. Вспомним, закон противоречия нарушается только тогда, когда речь идет об одном и том же предмете, в одно и то же время и в одном и том же отношении. В рассматриваемом высказывании речь идет о двух разных предметах: термин «детство» употребляется в различных значениях: детство как определенный возраст; детство как состояние души, пора счастья и безмятежности.

Таким образом, мнимое противоречие можно использовать как художественный прием. Достаточно вспомнить названия известных литературных произведений: «Живой труп» (Л. Н. Толстой), «Мещанин во дворянстве» (Ж. Мольер), «Барышня-крестьянка» (А. С. Пушкин), «Горячий снег» (Ю. В. Бондарев) и др. Иногда на мнимом противоречии строится заголовок газетной или журнальной статьи: «Знакомые незнакомцы», «Древняя новизна», «Необходимая случайность» и т. п.

Итак, закон противоречия запрещает одновременную истинность двух суждений, одно из которых нечто утверждает, а другое то же самое отрицает об одном и том же предмете, в одно и то же время и в одном и том же отношении. Однако этот закон не запрещает одновременную ложность двух таких суждений. Вспомним, суждения: «Он высокий», «Он низкий», — не могут быть одновременно истинными, если речь идет об одном и том же человеке, в одно и то же время его жизни и в одном и том же отношении (относительно какого-то одного образца для сравнения).

Точно так же одновременно ложными (но не одновременно истинными!) могут быть суждения: «Эта вода горячая», «Эта вода холодная»; «Данная речка глубокая», «Данная речка мелкая»; «Эта комната светлая», «Эта комната темная». Одновременную ложность двух суждений мы часто используем в повседневной жизни, когда, характеризуя кого-то или что-то, строим стереотипные обороты типа: «Они не молодые, но и не старые», «Это не полезно, но и не вредно», «Он не богат, однако и не беден», «Данная вещь стоит не дорого, но и не дешево», «Этот поступок не является плохим, но в то же время его нельзя назвать хорошим».

Подумайте

• В известной песне «Подмосковные вечера» есть такие слова: «…речка движется и не движется… песня слышится и не слышится…» Реальное или мнимое противоречие представляет собой эта фраза?
• Все помнят знаменитые слова из сказки Пушкина: «Кто на свете всех милее, всех румяней и белее?» Возможно, вы и раньше задумывались над тем, как можно быть румяней и белее одновременно. Реальное или мнимое противоречие присутствует в данном высказывании?

Суждения бывают противоположными и противоречащими. Например, суждения: «Сократ высокий», «Сократ низкий», — являются противоположными, а суждения: «Сократ высокий», «Сократ невысокий», — противоречащими. В чем разница между противоположными и противоречащими суждениями? Нетрудно заметить, что противоположные суждения всегда предполагают некий третий, средний, промежуточный вариант. Для суждений: «Сократ высокий», «Сократ низкий», — третьим вариантом будет суждение: «Сократ среднего роста». Противоречащие суждения, в отличие от противоположных, не допускают или автоматически исключают такой промежуточный вариант. Как бы мы ни пытались, мы не сможем найти никакого третьего варианта для суждений: «Сократ высокий», «Сократ невысокий» (ведь и низкий, и среднего роста — это все невысокий).

Именно в силу наличия третьего варианта противоположные суждения могут быть одновременно ложными. Если суждение: «Сократ среднего роста», — является истинным, то противоположные суждения: «Сократ высокий», «Сократ низкий», — одновременно ложны. Точно так же именно в силу отсутствия третьего варианта противоречащие суждения не могут быть одновременно ложными. Таково различие между противоположными и противоречащими суждениями.

Сходство между ними заключается в том, что и противоположные суждения, и противоречащие не могут быть одновременно истинными, как того требует закон противоречия. Таким образом, этот закон распространяется и на противоположные суждения, и на противоречащие. Однако, как мы помним, закон противоречия запрещает одновременную истинность двух суждений, но не запрещает их одновременную ложность; а противоречащие суждения не могут быть одновременно ложными, т. е. закон противоречия является для них недостаточным и нуждается в каком-то дополнении.

Поэтому для противоречащих суждений существует закон исключенного третьего, который говорит о том, что два противоречащих суждения об одном и том же предмете, в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными (истинность одного из них обязательно означает ложность другого, и наоборот).

Закон достаточного основания утверждает, что любая мысль (тезис) для того, чтобы иметь силу, обязательно должна быть доказана (обоснована) какими-либо аргументами (основаниями), причем эти аргументы должны быть достаточными для доказательства исходной мысли, т. е. она должна вытекать из них с необходимостью (тезис должен с необходимостью следовать из оснований).

Приведем несколько примеров. В рассуждении: «Это вещество является электропроводным (тезис), потому что оно — металл (основание)», — закон достаточного основания не нарушен, так как в данном случае из основания следует тезис (из того, что вещество металл, вытекает, что оно электропроводно). А в рассуждении: «Сегодня взлетная полоса покрыта льдом (тезис), ведь самолеты сегодня не могут взлететь (основание)», — рассматриваемый закон нарушен, тезис не вытекает из основания (из того, что самолеты не могут взлететь, не вытекает, что взлетная полоса покрыта льдом, ведь самолеты могут не взлететь и по другой причине).

Так же нарушается закон достаточного основания в ситуации, когда студент говорит преподавателю на экзамене: «Не ставьте мне двойку, спросите еще (тезис), я же прочитал весь учебник, может быть, и отвечу что-нибудь (основание)». В этом случае тезис не вытекает из основания (студент мог прочитать весь учебник, но из этого не следует, что он сможет что-то ответить, так как он мог забыть все прочитанное или ничего в нем не понять и т. п.)

В рассуждении: «Преступление совершил Н. (тезис), ведь он сам признался в этом и подписал все показания (основание)», — закон достаточного основания, конечно же, нарушен, потому что из того, что человек признался в совершении преступления, не вытекает, что он действительно его совершил. Признаться, как известно, можно в чем угодно под давлением различных обстоятельств (в чем только не признавались люди в застенках средневековой инквизиции и кабинетах репрессивных органов власти, в чем только не признаются на страницах бульварной прессы, в телевизионных ток-шоу и т. п.)

Таким образом, на законе достаточного основания базируется важный юридический принцип презумпции невиновности, который предписывает считать человека невиновным, даже если он дает показания против себя, до тех пор, пока его вина не будет достоверно доказана какими-либо фактами.

Закон достаточного основания, требуя от любого рассуждения доказательной силы, предостерегает нас от поспешных выводов, голословных утверждений, дешевых сенсаций, слухов, сплетен и небылиц. Запрещая принимать что-либо только на веру, этот закон выступает надежной преградой для любого интеллектуального мошенничества. Не случайно он является одним из главных принципов науки.

 

Подумайте

Выделите исходную мысль (тезис) и аргументы (основание) в приведенных ниже рассуждениях и определите, нарушен ли в них закон достаточного основания:

• Эти две прямые параллельны, поскольку у них нет общих точек.
• Эти две прямые параллельны, т. к. они лежат в одной плоскости и не имеют общих точек.
• Данное вещество является металлом, потому что оно электропроводно.
• Мой товарищ зарабатывает 10 000 долл. в месяц, в чем нельзя усомниться, ведь он сам это утверждает.
• В одном американском штате потерпела крушение летающая тарелка, ведь об этом писали в газетах, это передавали по радио и даже показывали по телевидению.
• Сегодня корабли не могут заходить в бухту, потому что она заминирована.
• Этот человек не болен, ведь у него не повышена температура.
• Данное слово надо писать с большой буквы, т.к. оно стоит в начале предложения.

 

Научитесь логично мыслить, думать и поступать:

Практическая логика и аргументация: практический интерактивный мультимедийный дистанционный курс

Законы логики

Три основных закона логики сформулированы Аристотелем:

А четвертый закон — достаточного основания — выдвинут немецким математиком и философом XVII—XVIII вв. Лейбницем.

1. Закон тождества.
Сущность закона: каждая мысль или понятие о предмете должны быть четкими и сохранять свою однозначность на протяжении всего рассуждения и вывода.

Нарушением этого закона является подмена понятий (часто используется в адвокатской практике).

В этом законе непосредственно проявляется природа самых фундаментальных свойств логической мысли — определенности и последовательности.

Иначе этот закон можно выразить так: мысли о предметах, свойствах или отношениях должны оставаться неизменными по содержанию в процессе всего рассуждения о них.

Причиной возникновения ошибок чаще всего является многозначность слов и, как следствие, нарушение закона тождества при рассуждении. Как, скажем, понимать такое предложение: «Партия фортепиано доставила большой коммерческий успех»? Идет ли здесь речь о блестящем исполнении и большом сборе благодаря нему или имеются в виду проданные за хорошую цену музыкальные инструменты?

Неоднозначность выражений может возникать и из-за двусмысленных грамматических конструкций. Путаница, вызванная такого рода обстоятельствами, знакома каждому благодаря знаменитому «казнить нельзя помиловать». «Беспечность порождает самонадеянность». В нем нельзя понять, что имеется в виду под порождаемым, а что под порождающим. Совершенно аналогичны в этом отношении выражения вроде: «Взвод сменяет караул» или «Меньшинство подчиняет большинство». Остроумно использовал двусмысленность выражения А.П. Чехов, вложив в уста одного из персонажей сообщение: «Перед вами череп обезьяны очень редкой разновидности. Таких черепов у нас всего два, один — в Национальном музее, другой — у меня».

Нельзя отождествлять различные мысли, нельзя тождественные мысли принимать за нетождественные. Результат применения — закон тождества обеспечивает определенность логического мышления.

2. Закон противоречия
Сущность закона: два несовместимых друг с другом суждения не могут быть одновременно истинными; по крайней мере одно из них обязательно ложно.

Закон противоречия раскрывает те же самые свойства определенности и последовательности, но только выражает их в отрицательной форме. Или, говоря немного конкретнее, согласно этой норме мышления в рассуждениях не должно быть одновременных утверждений и отрицаний относительно чего бы то ни было. Поэтому закон этот следовало бы назвать законом запрета противоречия. «Невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении» (Аристотель. Соч. Т. 1. С. 125). Признавать какое-либо положение и тут же от него отказываться всегда означает путаницу, отсутствие ясных и точных представлений. И когда нам надо показать несостоятельность, недопустимость тех или иных рассуждений или взглядов, то прежде всего мы стремимся указать на наличие в них нелепых, несовместимых положений — противоречий.

Может ли снаряд, пробивающий абсолютно все, пробить броню, которая абсолютно ничем не пробиваема?

Для ответа на этот парадокс достаточно еще раз взглянуть на формулировку второго закона, чтобы получить правильное решение.

При заданных условиях задача логически противоречива: всепробивающий снаряд и неразрушимая броня не могут существовать одновременно.

Еще один пример: так, тургеневский Рудин очень метко изобличает своего оппонента Пигасова в непоследовательности, когда тот делает воинствующе-нигилистические заявления насчет того, что никаких убеждений нет и быть не может, причем отстаивает) го свое пессимистическое мировоззрение горячо и убежденно.

— Так вы говорите: никаких убеждений нет? — спрашивает его Рудин.
— Нет и быть не может.
— Это ваше убеждение?
— Да.
— Как же вы говорите, что их нет? Вот вам одно на первый случай.

Утверждая что-либо о каком-либо объекте, мы не можем, не противореча себе, отрицать то же самое о том же самом объекте, взятом в то же самое время и в том же самом отношении. Второй закон обеспечивает непротиворечивость и последовательность мышления, способность фиксировать и исправлять всякого рода противоречия в своих и чужих рассуждениях,

3. Закон исключенного третьего.
Истинно либо суждение, либо его отрицание («третьего не дано»). Сущность закона: из двух противоречащих суждений если одно истинно, то другое ложно, а третьего не дано. Закон исключенного третьего применим к высказываниям противоречащим и не применим к высказывания противоположным.

Когда два понятия противоположны друг другу, то это означает максимальную противоположность между ними, а не просто противоречие. Выражается это в двух обстоятельствах: какой-нибудь признак, присущий одному из понятий, во-первых, отсутствует у другого и, во-вторых, вместо этого признака у него имеется несовместимый с ним (черный — белый, сильный — слабый, утро — вечер). Когда же у другого понятия отмечается только отсутствие какого-либо признака и ничего не говорится о том, какой ему вместо него присущ, то тогда возникает отношение противоречия: «белый» и «не белый», «утро» и «не утро», «добрый» и «недобрый», «экспорт» и «не экспорт».

Применяя закон исключенного третьего, надо помнить, что он ничего не говорит о том, какое из двух противоречащих суждений является истинным. Закон указывает лишь на то, что истинно одно, и только одно из них, а другое обязательно ложно. Это значит, когда нам удалось установить значение истинности одного из двух противоречащих суждений, то тем самым определилось и значение истинности другого. Отдельно устанавливать его уже не надо, потому что оно однозначно задается значением истинности сопряженного с ним понятия. Но какое именно из них должно быть оценено так, а какое иначе — для этого требуется отдельное исследование.

Нельзя уклоняться от признания истинным одного из двух противоречащих друг другу высказывай и искать нечто третье между ними. Посредством использования данного закона достигается однозначность логического мышления.

Закон достаточного основания
Сущность закона: всякая мысль может быть признана истиной только тогда, когда она имеет достаточное основание, всякая мысль должна быть обоснована. Всякая мысль истинна или ложна не сама по себе, а в силу достаточного основания. Это значит: любое положение, прежде чем стать научной истиной, должно быть подтверждено аргументами, достаточными для признания его твердо и неопровержимо доказанным.

Достаточным основанием какой-либо мысли может быть любая другая, уже проверенная и признанная истинной мысль, из которой вытекает истинность рассматриваемой мысли. Закон обеспечивает обоснованность мышления. Во всех случаях, когда мы утверждаем что-либо, мы обязаны доказать свою правоту, то есть, привести достаточные основания, подтверждающие истинность наших мыслей.

Законы логики — Гуманитарный портал

Законы логики (или логические законы) — это общее название множества законов, образующих основу логической дедукции (см. Дедукция). Понятие о логическом законе восходит к античному понятию о логосе (см. Логос) как о предпосылке объективной («природной») правильности рассуждений. Поскольку логика (см. Логика) изучает характер связи мыслей в процессе рассуждения, существуют определённые формальные и содержательные правила, следование которым обязательно. Различные по своей структуре и степени сложности рассуждения подчиняются разным правилам. Среди них можно выделить основные и производные: основные правила имеют более общий характер, производные — выводятся из основных. Наряду с этим существует такой тип правил логики, которые можно назвать всеобщими. Обычно такие правила называют законами мышления. Под законом вообще имеют в виду внутреннюю, необходимую и существенную связь явлений. Законы мышления представляют собой операциональные директивы мышления. Их происхождение обусловлено рациональной активностью субъекта. Выраженная в правилах, нормах, рекомендациях, целесообразная активность находит своё воплощение в принципах, имеющих всеобщий характер. В отличие от законов естествознания, которые описывают связь явлений природы, многократно повторяемую в идентичных условиях, законы мышления предписывают определённые способы интеллектуальной деятельности. Цель законов логики — сформулировать основания правил и рекомендаций, следуя которым можно достичь истины. Поэтому законы мышления не являются законами в том смысле, в котором указанный термин используется для описаний явлений природы. Таким образом, законы логики представляют собой законы правильного мышления человека о мире, а не законы самого мира. Правила мышления впервые получают логическое содержание у Аристотеля, положившего начало систематическому описанию и каталогизации таких схем логических связей элементарных высказываний в сложные, истинность которых вытекает из одной только их формы, а точнее — из одного только понимания смысла логических связей, безотносительно к истинностному значению элементарных высказываний. Большинство логических законов, открытых Аристотелем, представляют собой законы силлогизма. Позже были открыты и другие законы, и даже было установлено, что совокупность законов логики бесконечна. В некотором смысле рассмотреть эту совокупность удаётся с помощью различных формальных теорий логического рассуждения — так называемых логических исчислений, в которых интуитивное понятие «логический закон» реализуется в точном понятии «общезначимой формулы» данного исчисления, что, в свою очередь, делает понятие «логический закон» относительным. Однако типом логического исчисления полагаются одновременно и границы этой относительности. При этом тип исчисления, как правило, не является делом произвольного выбора, а диктуется (или подсказывается) «логикой вещей», о которых хотят рассуждать, а также нашей субъективной уверенностью в том или ином характере этой логики. Исчисления, основанные на одной и той же гипотезе о характере «логики вещей», являются эквивалентными в том смысле, что в них каталогизируются одни и те же логические законы. Например, исчисления, основанные на гипотезе двузначности, несмотря на всё их внешнее разнообразие, описывают одну и ту же область классических законов логики — мир тождественных истин (или тавтологий), издавна получивших философскую характеристику «вечных истин» или «истин во всех возможных мирах» (см. Возможные миры). Логикой вещей, отражением которой исторически явились логические законы так называемой интуиционистской логики, является логика умственных математических построений — «логика знания», а не «логика бытия». Логические законы отличаются от логических правил вывода. Первые представляют класс общезначимых выражений и формулируются в объектном языке исчисления. Вторые служат для описания фактов логического следования (см. Логическое следование) одних выражений из других, не обязательно общезначимых, и формулируются в метаязыке исчисления. В отличие от законов логики, правила вывода имеют вид предписаний и носят, по существу, нормативный характер. При построении исчислений без правил вывода обойтись нельзя, а без законов логики, в принципе, можно (именно так и поступают в исчислениях естественного вывода). Тем не менее, изучение логических законов образует естественный исходный пункт логического анализа приемлемых (логически правильных) способов рассуждений (умозаключений), поскольку понятие «приемлемое» или «логически правильное» рассуждение уточняется через понятие «логический закон». В традиционной формальной логике термин «закон логики» имел узкий смысл и применялся только к четырём так называемым основополагающим законам правильного мышления — к закону тождества, закону непротиворечия, к закону исключённого третьего и к закону достаточного основания: Закон тождества. В процессе умозаключения всякое высказывание и суждение должны оставаться тождественными самим себе (см. Закон тождества). Закон непротиворечия. Два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении (см. Закон непротиворечия). Закон исключённого третьего. Из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано (см. Закон исключённого третьего). Закон достаточного основания. Никакое суждение не может утверждаться без достаточного основания (см. Закон достаточного основания). Указанная «канонизация» термина «закон логики» в настоящее время является данью традиции и не отвечает действительному положению вещей. Тем не менее, эти законы можно принять в методологическом смысле как определённые принципы (или постулаты) теоретического мышления, так как они являются наиболее общими и используются при оперировании понятиями и суждениями, в умозаключениях, доказательствах и опровержениях, и поэтому присутствуют практически во всех логических системах. В этом смысле закон тождества (lex identitatis) истолковывается как принцип постоянства или принцип сохранности предметного и смыслового значений суждений (высказываний) в некотором заведомо известном или подразумеваемом контексте (в выводе, доказательстве, теории). В языке логических исчислений указанная сохранность обычно выражается формулой A ⊃ A. Принятие закона тождества для суждения A не означает, вообще говоря, принятия самого A. Но если A принято, то закон тождества принимается с необходимостью для исчислений с общезначимой формулой A ⊃ (A ⊃ A). Для исчислений, включающих отрицание, это сведение абстракции постоянства суждения к принятию самого суждения имеет форму закона: (A ⊃ ¬ (A ⊃ A) ⊃ ¬ A), то есть если при допущении суждения для него отрицается закон тождества, то тем самым отрицается и само это суждение. Закон непротиворечия (lex contradictionis) указывает на недопустимость одновременного утверждения (в рассуждении, в тексте или теории) двух суждений, из которых одно является логическим отрицанием другого, то есть суждений вида A и ¬ A или их конъюнкции, или эквиваленции, или — в более широком смысле — утверждений о тождестве заведомо различных объектов, поскольку обычно правила логики таковы, что позволяют из противоречия выводить произвольные суждения, что обесценивает содержательный смысл умозаключений или теорий. Наличие противоречия в рассуждении (теории) создаёт парадоксальную ситуацию и нередко указывает на несовместимость посылок, положенных в основу рассуждения (теории). Этим обстоятельством часто пользуются в косвенных доказательствах. Закон исключённого третьего (lex exclusii tertii) на логическом языке записывается формулой A ⌵ ¬ A и утверждает, что нет ничего среднего (промежуточной оценки) между членами противоречивой пары (отсюда другое латинское название этого закона — tertium non datur). В методологическом плане этот закон выражает конструктивно неоправданную идею о разрешимости (потенциально осуществимом указании на истинность или ложность) произвольного суждения. В отличие от формулы, соответствующей закону противоречия, формула, соответствующая закону исключённого третьего, не выводима в интуиционистских и конструктивных исчислениях, хотя и неопровержима в них. Дихотомия установленных истины и лжи неоспорима, но дихотомия утверждения и отрицания оспаривалась неоднократно. Наиболее последовательную критику закона исключённого третьего дал Л. Э. Я. Брауэр. В свете его критики этот закон следует рассматривать только как принцип (или постулат) классической логики. Закон достаточного основания (lex rationis determinatis seu sufficientis) выражает методологическое требование обоснованности всякого знания, всякого суждения, которое мы хотели бы принять за отображение истинного (действительного) положения вещей. В этом смысле он применим не только к выводному знанию (в частности, к аксиомам и постулатам научных теорий), но и ко всей области фактических истин, не имеющих отношения к формальной логике. Не случайно Г. В. Лейбниц, который ввёл этот принцип в научный обиход, относил его в первую очередь не к логике, а ко всем событиям, которые случаются в мире. В приложениях логических законов к конкретным ситуациям с особой наглядностью обнаруживается их общая черта: все они представляют собой тавтологии и не несут содержательной, «предметной» информации. Это — общие схемы, отличительная особенность которых в том, что, подставляя в них любые конкретные высказывания (как истинные, так и ложные), мы обязательно получим истинное выражение. Указанные законы мышления имеют в логике такое же значение, какое в математике имеют аксиомы (см. Аксиома) или постулаты и обладают таким же формальным характером, как и формулы алгебры: в последних не говорится о том, по отношению к каким числовым значениям они выполняются, а законы мышления не содержат в себе содержательных характеристик, то есть не квалифицируют то, что именно должно или не должно отождествляться, что именно и чему должно или не должно противоречить, и так далее. Именно в этом и заключается их обобщающий характер как операциональных директив правильного мышления и рассуждения.

ТОП 10! Универсальные ЗАКОНЫ ЛОГИКИ + ТАБЛИЦА!

Основные законы логики в полном составе – все 10 штук. Законы логики от Аристотеля, Лейбница, Клавия, Пирса, де Моргана. Пусть ваша логика станет безупречной!

Логика – наука, ориентированная на познавательную деятельность человечества. В поле ее зрения находятся и самые разнообразные формы мышления, и возникающие в мыслительном процессе отношения между ними. Считается, что есть женская логика, есть мужская, но в действительности логическое мышление не разграничивается по половому принципу, так как мыслительным процессом управляют одни и те же законы.

Содержание:

1. Закон тождества 
2. Закон исключенного третьего
3. Закон непротиворечия 
4. Закон достаточного основания  
    УПРАЖЕНЕНИЯ. Отыщи, где нарушена логика
5-10. Математические законы логики: Клавия, Пирса, де Моргана…
    ТАБЛИЦЫ с формулами основных логичесских законов

Для чего нужна логика? Чтобы грамотно, последовательно и эффективно доносить свою позицию до собеседника. Без соответствующих умений делать это очень непросто. В своей речи вы должны последовательно и непротиворечиво излагать свою позицию, не забывая о логических связках между высказываниями. Последнее особенно важно, так как «Попытка нарушить закон природы способна убить вас, но точно так же попытка нарушить закон логики убивает в вас разум», — заявлял в свое время Александр Леонидович Никифоров, известный деятель науки, философ и теоретик.

Далее мы познакомим вас не только с тремя законами логики, открытыми еще древнегреческим мыслителем Аристотелем (закон тождества, закон (запрета) противоречия, закон исключенного третьего), но и с законом достаточного оснвания Лейбница, а также соответствующими математическими открытия в области логики, сделанными другими учеными – в общей сложности до 10!

Первые четыре из законов логики, которые мы рассмотрим, определяются, как формальные и называются основными. Углубляясь немного в историю, отметим, что под логическим законом еще Аристотель понимал предпосылку к объективным, заложенным природой, правильным размышлениям.

Сегодня под термином Логический закон понимается существенная, сокрытая внутри высказывания необходимая связь между логическими формами, обнаруживающая себя по ходу построения рассуждения. Для наглядности, основные законы логики принято записывать в виде соответствующих формул. Они часто встречаются в учебниках, всевозможных пособиях и научных трудах, но сами ученые называют их определенную условность, так как они лишь схематично обозначают сущность законов логики.

---

В тексте «Метафизики» Аристотель подчеркивал, что размышление в принципе нельзя осуществить (оно будет несостоятельным) «если каждый раз не мыслить что-нибудь одно». Сегодня эта фраза излагается несколько иначе. В учебных материалах по логике распространено такое определение: «Любое высказывание (суждение, мысль, а также понятие) неукоснительно должно сохранять один и тот же смысл в течение всего рассуждения».

Современные нам исследователи подчеркивают, что различные мысли запрещается принимать за тождественные, а тождественные за различные. Дело в том, что в обычной речи (особенно при пересказе) зачастую кажется, будто без труда можно выразить одну мысль другими словами. Это очень опасное заблуждение, так как в результате оно может привести к замене одной мысли другой (то есть изначальный смысл будет полностью утерян).

Рассмотрим случаи нарушения закона тождества на примерах:

А) Ученики прослушали объяснение учителя

Б) На турнире рассеянный шахматист много раз терял очки

Видите, как ярко, очевидно нарушается закон тождества во фразе под номером А. Обратить внимание нужно на словосочетание «ученики прослушали». С одной стороны школьники могли внимательно ВЫСЛУШАТЬ преподавателя, а с другой — пропустить все сказанное им мимо ушей. Получается, что из-за малейшего нюанса меняется смысл всей фразы.

Аналогично от нас ускользает смысл предложения «На турнире рассеянный шахматист много раз терял очки». Без дополнительной информации мы не можем понять – те ли очки он терял, которые присуждают успешным спортсменам, или те, которые у него на носу?! Вот так и выходит, что тождественными друг другу представляются в рамках одной фразу сразу две ситуации – одна трагическая, а другая комическая.

Необходимость применения при построении логических фраз закона тождества Аристотель обосновал, обратившись к софизмам (это такие высказывания, которые, если не вдумываться, кажутся верными, однако в сути своей ложные). Вот несколько софизмов, в которых нарушается закон тождества:

А) 8 и 5 это нечетное и четное числа. При этом в совокупности 8 и 5 равняются 13. То есть 13 это одновременно нечетное и четное число.

Б) То, что наполовину наполнено – наполовину пусто. Раз половины равны, то равны и целые части. То есть полное это тоже, что и пустое.

Если рассмотреть все представленные выше примеры, то можно проследить, что несмотря на кажущуюся верность рассуждений во всех случаях нарушен закон тождества. Если разобрать пример А, то видно, что один и тот же союз в двух первых предложениях (союз «и») имеет разное значение. Вначале он носит объединяющий характер (в значении «и то и другое»), в затем недвусмысленно указывает на факт сложения двух чисел. Так и выходит – раз в процессе размышлений к одному предмету (или к слову, как в нашем случае) применялись разные смыслы. В результате имеем нарушение закона логики – то есть в целом высказывание неверно.

Всякий софизм в своей сути (даже весьма тонкий) построен по накатанной дорожке – в них всегда не очень заметно соотносятся совершенно нетождественные друг с другом предметы или ситуации, события и высказывания. При этом соблюдается внешняя правдоподобность таких «неправдивых» фраз.

Опасайтесь софистов в обычной жизни, то и дело нарушающих законы тождества и порою стремящихся обвести вас вокруг пальца. Особенно популярен софизм в телевизионной и прочей рекламе товаров и услуг. Как вам такой софизм?:

Ответь, что круче: жизнь в раю после смерти или сникерс? Разумеется жизнь в раю после смерти! А что вообще может быть круче жизни в раю после смерти? Да нет ничего круче! Но сникерс лучше, чем ничего, а раз так, то он круче, чем жизнь в раю после смерти!

Между прочим, на нарушениях закона тождества плодятся не только одни софистические высказывания. С их помощью можно неплохо пошутить в литературном произведении! Возьмем, к примеру «Мертвые души» Николая Васильевича Гоголя. С нарушением логического закона тождества автор описывает Ноздрева, как «исторического человека». Почему? Да потому, что где бы он ни появлялся – с ним непременно происходила некая «история».

В афоризмах также нередко нарушается закон тождества: «Не стой где попало, а то еще попадет». Не забывают о таком приеме и авторы анекдотов:

– Я проломил себе череп в трех местах.
– Лучшие не ходи в такие места.

– В вашем отеле имеются номера, где тихо?
— В наших номерах везде тихо, что не скажешь о шумных постояльцах

– Вовчик, а ты нырнуть прямо сейчас в воду смог бы?
– Смог бы.
– И как долго сможешь не всплывать?
– Да пока меня из воды не выволокут.

– Эх, какие мечты в детстве были. Твои хоть какие-то сбылись?
– Ну да. С детства не любил парикмахера и мечтал никогда к нему не ходить.
— Ага, с лысой башкой это не к чему.

– Вова! Почему опаздываем на первый урок?
– Мне хотелось отправиться порыбачить с папой, однако меня не взяли.
– Отлично! Папа же тебе сказал, отчего ты должен предпочесть занятия рыбной ловле?
– Конечно. Он решил, что раз червей накопали только на одного рыбака, то второму с удочкой делать нечего.

Бабуля объясняет маленькому Вове почему алкоголь до 18 вреден:
– Да брось ты, дед всю жизнь пробухал – ни одного дня трезвым не видели! Вчера ему 80 лет исполнилось!
Бабуля находчиво отвечает:
– А не бухал бы – так ему и вовсе 90 было бы!

Экзамен. Суровый препод спрашивает:
– Фамилия, уважаемый?
– Сидоров.
– Что улыбаемся Сидоров?
– Радостно мне!
– Это ж почему?
– Так я уже на ваш первый вопрос ответил!

Лишь только деду нашему стукнуло 60 – он стал пробегать по 5 км в день. Сегодня ему за 80, и мы даже представить не можем где он бегает.

– Доченька! Твой жених хром на обе ноги, косит левым глазом, правый не видит… Родных у него нет – умерли давно. Безработный к тому же. Не выходи за него!
– А не нужен мне принц на белом коне – красивый или богатый. Я в любовь верю!
– Эх, не про то я. Парнишка этот и так в жизни горя хлебнул, а тут еще ты на его шее повиснешь…

Нарушение закона тождества – лучший конструктор для головоломок и задач на развитие интеллекта. Вот одна из них: спросите своего друга: «Зачем (на самом деле — «за чем»!) находится вода в стакане из стекла?» Этим вопросом мы специально моделируем ситуацию с двумя смыслами. С одной стороны «зачем» – подразумевает «для чего», с другой под «за чем» мы хотим узнать за каким именно веществом или предметом спрятана (находится) вода. Добровольный участник вашего коварного эксперимента обычно на озвученный выше вопрос отвечает не задумываясь, что-то вроде: «Зачем? Ну, чтоб пить. Чтобы цветочки орошать». Мы же говорим ему гордое «нет! Не угадал!» и всеми правдами и неправдами пытаемся выдавить правильное решение головоломки. Он должен ответить: «За стеклом!».

Подводя итог главы, отметим, что для соблюдения закона тождества, изначальные мысли по ходу рассуждения не нужно менять. Для практического его применения всего-то и нужно, что вступая в дискуссию или составляя речь – стараться четко представлять предмет рассуждения. Это даст возможность уйти от ненужных двусмысленностей и потери первоначального смысла.
Конечно, закон тождества совсем не указывает на то, что есть в нашем бренном мире вещи извечные, неподверженные никаким изменениям. Он не настолько глобален. Его смысл в том, что человеческая мысль, помещенная в рамки языковой фразы, останется тождественной себе даже с учетом некоторых речевых преобразований.

 

---

Это, пожалуй, наиболее известный из всех законов логики Аристотеля, который особенно прославила и растиражировала по свету латинская фраза «tertium non datur» (или третьего не дано). В чем суть закона исключенного третьего? Все просто. Если о предмете утверждается какая-та истина (первое суждение), и если кем-то эта истина опровергается (второе суждение), то только одно из них должно быть верным – третьему путь заказан!

«…нет ничего посреди меж двух противоречивых суждений об одном, — в Третьей Книге «Метафизики» отмечал Аристотель, — всякий отдельный предикат следует либо отрицать, либо утверждать». Греческий философ очерчивал границы применения закона третьего лишнего. По его словам, использовать его можно было только в разговорах о прошедшем и настоящем времени. Табу на применение правила накладывалось только на будущее время, так как сложно уверенно утверждать состоится то или иное событие или нет.

Очевидно, что закон непротиворечия и закон исключенного третьего тесно связаны. Действительно, те суждения, которые подходят под действие закона исключенного третьего, подходят и под закон непротиворечия, но не все суждения последнего, попадают под действие первого.

Ниже мы приведем несколько формул, в которые можно вписать закон исключенного третьего:

А) «X не есть Y» и «Y есть X»
Суть формулы: Одно и тоже суждение отрицает нечто о предмете в определенном отношении и определенном времени, при этом второе суждение тоже самое утверждает. В качестве примера: «Медведи – грызуны» и «Медведи – не грызуны».

Б) «Некоторые X не есть Y» и «Все X есть Y»
Суть формулы: Некое суждение утверждает нечто по отношению ко всему классу предметов, при этом второе суждение это отрицает, однако по отношению только к некоторой части этих предметов. В качестве примера: «Все солдаты Западного фронта получили медаль за отвагу» и «Отдельные солдаты Западного фронта получили медаль за отвагу».

В) «Некоторые X есть Y» и «Ни одно X не есть Y»
Суть формулы: Определенное суждение полностью отрицает наличие характеристики у класса вещей, при этом второе суждение такую характеристику утверждает, однако — в отношении лишь части этих предметов. В качестве примера: «Ни один житель нашего дома не пользуется Интернетом» и «Некоторые жители нашего дома пользуются Интернетом».

Этот закон Аристотеля в свое время был подвержен критике со стороны других философов. Особенно стали цепляться к нему во времена Новой истории. Все злопыхания можно свести к словесной формуле следующего типа: «Можно ли с полной уверенностью считать всех лебедей мира черными, отталкиваясь лишь от такой посылки, что до сих пор нам попадались на глаза лишь птицы этого цвета?». То есть, ученые считают, что зачастую закон Исключенного третьего применим только в двузначной, основанной на абстракции, логике Аристотеля. А так как в реальной жизни ряды элементов теряются в бесконечности – исключить все возможные альтернативы очень сложно. Поэтому приходится задействовать иные логические принципы.

Закон исключенного третьего плотно взаимодействует с еще одним законом логики Аристотеля — законом непротиворечия. И о нем – ниже.

 

---

Очередной формальный закон логики утверждает, что оба друг с другом несовместимых суждения не способны в одно и тоже время оказаться верными – среди них имеется хотя бы одно ложное. Закон непротиворечия таким образом словно следует из закона тождества. «Это нереально, чтобы нечто в одно время было присуще, а также не было присуще чему-то…, — утверждал в своих трудах Аристотель. Чтобы лучше понять мысль известного грека, обратимся к примерам. Ниже приведем две взаимоисключающие фразы:

А) Всякий, кто зашел на интернет-ресурс iq230.com – закончил университет с красным дипломом.

Б) Никто из посетивших интернет-ресурс iq230.com не закончил университет с красным дипломом.

Логика поможет нам разобраться в том, какое из представленных суждений истинное, и есть ли истинность в них вообще. Изучив фразы А и Б, мы способны предположить, что обе они в одно и тоже время не способны оказаться истинными, так как на лицо явное противоречие. Из этого следует сразу несколько важных вещей. Во-первых, если удастся доказать, что одно из них истинно, следовательно второе будет ложным. Во-вторых, если мы докажем ложность одной из фраз, то вторая с одинаковой долей вероятности может оказаться и истинной, и ложной. Соответствующего опроса наш ресурс среди посетителей не проводил, но если вдуматься, то оба представленных выше утверждения должны показаться вам ложными.

Закон непротиворечия (противоречия) ставит запрет на одновременное утверждение и отрицание чего-то одного. С одной стороны это правило кажется на 100% очевидным и даже возникают сомнения в необходимости формулировки такого очевидного закона логики. Но не все так просто. Необходимо изучить условия, при которых данный принцип нарушается.

Так, к примеру, нарушение закона непротиворечия произойдет в случае, если две последующие фразы будут произнесены с учетом современных реалий российской действительности («Санкт-Петербург не является столицей Российской Федерации» и «Санкт-Петербург является столицей Российской Федерации»). Другое дело, если оба эти утверждения звучат не в едином контексте, а относятся к разным эпохам. В таком случае все верно: Сегодня Санкт-Петербург и в самом деле не является столицей Российской Федерации. При этом город на Неве являлся столицей, если речь идет в русле событий 18 века.

Вот еще один красноречивый пример аналогичного казуса. «Я отлично говорю по-французски», а также «Я посредственно говорю по-французски». И то и другое утверждение могут оказаться верными, если речь в них идет о разных вещах. Например, в университете я сдал экзамен по французскому языку на отлично, следовательно — я отлично говорю по-французски! Обрадованный, я пошел устраиваться в контору переводчиком, а там меня зарубили на тестировании – для работодателя мой уровень владения языком оказался недостаточным. Вывод? Я посредственно говорю по-французски!

Контактные противоречия в логике. Примечательны они тем, что встречаются крайне редко, но если звучат из речи политиков, то на них тут же обращаешь внимание. Когда возникают контактные противоречия? Происходит это когда практически одновременно нечто называется ложным, а затем – буквально в следующем предложении – истинным.

Дистантные противоречия в логике более распространены. Суждения подобного рода (также диаметрально противоположные) звучат не одно за другим, а спустя определенное время. Нужно постоянно следить за тем, чтобы не сбиться с первоначального пути. Такую ошибку зачастую допускают начинающие журналисты и научные работники. Хотите примеров?

Вот небезынтересный ляп из учебника по литературе. С интервалом в несколько страниц в нем утверждались две взаимоисключающие вещи «Уже с самого начала своего творчества Маяковский обладал качествами, которые существенно отличали его от представителей футуризма» и вот еще «В первый период творчества Маяковский ничем не отличался от футуристов».

При этом противоречия бывают также неявными и явными. В первом случае противоречие следует из контекста фразы, словами оно не сформулировано, однако подразумевается. Во втором же — одна мысль непосредственно противоречит другой. Явных контактных противоречий не так много в повседневной жизни – другое дело симбиоз неявных с дистантными.

Неявные противоречия, как и дистантные, в силу своей незаметности намного более распространены в мышлении и речи. Явные противоречия (также как и контактные) наоборот — встречаются редко. Их примером могут послужить следующие фразы:

Таксист при выезде со стоянки нарушил правило, так как не соизволил взять устного разрешения в письменной форме.

Юная особа престарелого возраста с еле заметным ежиком рыжих волос до пояса, изящно прихрамывая, предстала перед публикой.

Столь очевидные противоречия часто применяются юмористами и литераторами для придания комического эффекта. А вот другие группы противоречий, уже не столь явные, больше напоминают ошибки и с ними нужно бороться. Вот пример такого «ошибочного» неявного и одновременно контактного противоречия «Данная рукопись создана в XI веке на Руси». Ничего подозрительного не заметили?! А подозрительное есть! В этот период времени на Руси еще не было писчей бумаги!

Не забудем упомянуть и про мнимые противоречия. Говоря кратко – это особенная смысловая (речевая) конструкция, только кажущаяся противоречивой, но на самом деле таковой не являющаяся. «В детстве у меня не было детства», — поговаривал Антон Павлович Чехов, вспоминая юные годы. Если постараться разобрать эту фразу не вникая, то можно предположить, что известный прозаик утверждает две диаметрально противоположные вещи: с одной стороны у него есть детство, а с другой – нет. Это мнимое противоречие и закон непротиворечия здесь не нарушен, так как речь в высказывании Чехова идет не об одном и том же предмете в одно и тоже время: с одной стороны – это определенный возраст, с другой – состояние души, время особого счастья и безоблачной радости. Такое мнимое противоречие специально используется Чеховым. С его помощью он достигает наилучший художественный эффект.

Мнимое противоречие – прием, который с удовольствием использовали и используют сотни известных авторов литературных произведений. Его можно даже в названии классических произведений найти! У Льва Николаевича Толстого было замечательного произведение «Живой труп», у Александра Сергеевича Пушкина – «Барышня-крестьянка». Подобных произведений в мировой литературе масса: «Мещанин во дворянстве», «Горячий снег» и т.д. Журналисты таким приемом тоже не брезгуют: «Нищий олигарх», «Родной враг», «Честный жулик»…

Особенно хороши мнимые противоречия в афоризмах:

Эйнштейн: Самое непостижимое в мире кроется в том, что он постижим
Сократ: Я знаю лишь то, что ничего не знаю
Пушкин: Слышу умолкнувший звук божественной эллинской речи
Гегель: История учит только тому, что она ничему не учит

Подводя итог, отметим, что закон противоречия (непротиворечия) «специализируется» на связях между логическими противоречиями (двумя противоположными по смыслу суждениями), совершенно не затрагивая противоположных граней единого предмета. Знание такого закона и следование ему дисциплинирует мыслительную деятельность и позволяет избегать досадных ошибок.

 

---

Вот мы и добрались до 4-го формального закона логики. И так вышло, что вывел его не Аристотель, а математик и философ Готфрид Лейбниц в научном труде «Монадология» (1714 год). В своей работе немецкий ученый подчеркнул «…ни одно из существующих явлений не будет действительным или истинным, и ни одно утверждение не будет справедливым без достаточного основания, без указаний почему дело обстоит именно так, и никак по другому (пусть даже такие основания в большинстве случаев не могут быть нам известны)».

Более приближенный к нам во времени Готфрид Лейбниц считает, что для того, чтобы называться достоверным, любое положение необходимо доказать. А для этого необходимы основания, причем – в полном объеме. То есть, закон достаточно основания напоминает логику о необходимости быть обоснованным в своих суждениях.

Своим вкладом в логику Готфрид Лейбниц связал законы Аристотеля и условия их определенности, непротиворечивости, а также последовательности и рассуждения. Известный математик намекает, что в действительности одного лишь истинного суждения недостаточно. В практической жизни или познавательной деятельности людям этого мало – нужно уметь обосновывать свою позицию.

Закон достаточного основания применяется нами регулярно. Всякий раз, когда мы делаем выводы, используя для этого основание (факты) – мы совершаем то, о чем говорил Лейбниц три века тому назад. Обычное дело, когда научный работник в конце своей кандидатской или докторской диссертации помещает «список использованной литературы». Этим он подкрепляет основную идею своего исследования и работает в русле закона достаточного основания.

Не обязательно быть деятелем науки, чтобы применять правило Лейбница в повседневной жизни. Этим занимаются чуть ли не все российские граждане: школьники, студенты, журналисты, а уж как востребован закон достаточного основания в судебной сфере! При подготовке обвинительного заключения или позиции защиты без него никуда.

Интересно, что часто закон Лейбница нарушают, причем – и не только в связи с неграмотностью отдельных людей. Иногда это делается, чтобы обвести собеседника вокруг пальца. Например: «Сергей полностью здоров, так как у него не течет из носа» или «Чикатило Чикатилович не способен расчленять маленьких девочек, ведь все его знают в качестве ударника труда, замечательного мужа и отца». Не нужно быть семи пядей во лбу, чтобы узнать, где аргументы в представленных выше фразах недостаточно обосновывают основное утверждение.

Ниже представлены некоторые формы нарушения рассматриваемого нами закона логики:

— Миша обсолютно здоров, так как он подтянулся больше всех в классе

— В Костромской области пьяные охотники съели снежного человека и это правда, ведь про этот факт трезвонили во всех местных газетах

— Ты виноват уж тем, что хочется мне кушать (цитата из басни Крылова)

Водой успешно уничтожают пожары по причине, что она текучая и ее температура ниже, чем у огня.

Тот, кто соблюдает закон достаточного основания, успешно избегает в своих выводах скорых, необдуманных утверждений, голословных фраз. Здесь уже нет места для слухов, басенок и сплетен. Закон достаточного основания позволяет избегать любых мистификаций и неплохо отражается в поговорках:

Доверяй, но проверяй

Язык без костей

Не верь своим глазам (вариант – «ушам»)

Говорят так, словно кур доят

Никакому интеллектуальному мошенничеству не обойти закон достаточного основания! Он дает запрет на слепую веру в чудеса и зримо разграничивает истинную науку от псевдонауки (астрология, нумерология, алхимия и много других).

Так как любая лженаука старается выглядеть солидно (даже прикрываясь авторитетом истинных научных дисциплин) – настоящим ученым просто необходимо пользоваться законом достаточного основания. В его русле ученые и стараются работать, опираясь на важнейшие принципы:

1. Принцип верификации (термин имеет латинское происхождение от слов Veritas и facere, которые переводятся как «истина» и «делать») предписывает понимать под научным лишь знание, истинность которого есть возможность подтвердить – раньше или позже, прямо или косвенно. Еще в 20-м веке англичанин и философ Бертран Рассел предложил руководствоваться этим принципом.
К сожалению, сегодня псевдонауки настолько поднаторели в запудривании мозгов, что складывается впечатление, словно все их доводы легко подтверждаемы. Поэтому в помощь принципу верификации ученое сообщество добавило и принцип фальсификации. Его предложил в свое время другой (уже немецкий) философ 20-го века Карл Поппер.

2. Принцип фальсификации (термин имеет латинское происхождение от слов false и facere, которые переводятся как «ложь», «делать») утверждает, что лишь такое знание считается научным, которое можно опровергнуть – раньше или позже, прямо или косвенно.

Не звучит ли для вас определение принципа фальсификации не совсем логичным. Неужели подлинное научное знание – то, которое опровергается? Как бы ни звучало это дико, но все обстоит именно так. Современная наука не стоит на месте, практически все теории со временем опровергаются новыми. Для движения вперед важна не одна лишь подтверждаемость научной мысли, но и возможность ее опровергнуть. Примеров можно привести массу. Древние, к примеру, считали, что Земля – центр вселенной, а Солнце и звезды кружатся вокруг нее. Вера в это сохранялась 2000 лет! Исходя из этого убеждения, ученые совершили массу «открытий». Теперь это представление считается устаревшим и все наработки того периода опровергнуты. Лишь в 15 веке человечество пришло к мысли, что это Земля кружится вокруг Солнца, а не наоборот.

Если один из представленных выше принципов (верификации) адепты псевдонаук еще могут обойти, но испытание принципом фальсификации они пройти не могут. Тот, кто исповедует псевдонауку, согласится с тем, что все в его «научной дисциплине» подтверждается фактами, но он никогда не признает, что со временем это может быть опровергнуто новым знанием. Он считает, что его древняя наука, впитавшая в себя мудрость веков – абсолютно верна, непогрешима и неопровержима. Так что если кто-то однажды скажет вам, что его научное знание неопровержимо, будьте уверены – вы имеете дело с последователем лженауки. Настоящий ученый легко признает, что теория, которой он, возможно, посвятил многие годы своей жизни, со временем может быть опровергнута другими исследованиями.

В отличие от серьезных научных дисциплин псевдонаука не развивается, а стоит на месте. Все ее выводы и теории – неизменны с момента зарождения, что роднит лженауку с деятельностью диких шаманов и колдунов.

 

Тренировка Логического мышления

---

1) Скажите, какой закон формальной логики нарушен:

(Наследие Гоголя)
Один там только и есть порядочный человек: прокурор. Да и тот, если сказать правду, свинья»

(Наследие О.Хайяма)
Дураки мудрецом почитают меня,
Видит Бог: я не тот, кем считают меня.
О себе и о мире я знаю не больше
Тех глупцов, что усердно читают меня

(Наследие Мольера)
— Конечно, Вы хотите написать ей стихи?
— Нет, нет, только не стихи.
— Вы предпочитаете прозу?
— Нет, я не хочу ни прозы, ни стихов».

2. Какая из представленных внизу фраз может стать основой для еще одной из этого списка:

— Иванов не станет смеяться над пошлой шуткой.
— Иванов, как правило, не сеется над пошлыми шутками.
— Иванов вряд ли станет смеяться над данной шуткой.

3. Можно ли сказать, что в представленной ниже фразе нарушается закон исключенного третьего:

Про Иванова не скажешь, будто этот человек бездельник и лентяй. Также не стоит говорить, что он не бездельник и не лентяй

4. Взяв на вооружение закон непротиворечия, скажите, являются ли представленные ниже фразы одновременно истинными и почему:

В лесу все березы покрылись почками. Не все березы в лесу покрылись почками.

В лесу все березы покрылись почками. Многие березы в лесу покрылись почками.

Очень немногие школьники 3-го А осилили этот диктант. Ни одному школьнику 3-го А не удалось осилить этот диктант.

Есть люди, которые поучают большое удовольствие от чтения Толстого. Есть люди, которые не получают большого удовольствия от чтения Толстого.

5) Скажите, какой закон формальной логики нарушен:

Все пожарные знают как эффективно тушить пожар. Иванов знает, как эффективно тушить пожар, значит он — пожарный.

Маруся посетила доктора философии, чтобы он выписал ей лекарство от гриппа.

6) А теперь, уважаемые читатели, постарайтесь сами придумать пару-тройку примеров, в которых формальные законы логики безбожно нарушаются.

 

5-10. Математические законы логики: Клавия, Пирса, де Моргана и др.

---

Ниже мы рассмотрим более сложные, в основном применяемые в сферах математики законы логики. Чтобы не перегружать читателя сложной информацией с обилием математических формул, мы свели соответствующие формулировки и определения к минимуму.

Закон двойного отрицания

Еще один из важнейших принципов классической логики — закон двойного отрицания утверждает следующее: «если неверным считается то, что неверно А, то следовательно А — верно». Альтернативное название для этого логического закона — закон снятия двойного отрицания.

Особое распространении логический закон двойного отрицания имеет в традиционной содержательной математике, где он является веским доводом к проведению доказательств от противного. Такие доказательства проходят интересным образом. Первым делом из некого предположения о том, что определенное суждение А не является верным, выводится противоречие в конкретной теории. Затем на основании непротиворечивости теории появляется вывод, что в действительности неверным является «не А». В результате по закону двойного отрицания делается вывод о том, что А верно.

Отметим, что при конструктивных рассмотрениях в математике закон двойного отрицания оказывается неприемлем, особенно если имеет место требование алгоритмической реализуемости обоснования математических суждений.
Стоит подчеркнуть, что закон двойного отрицания плотно взаимодействует с законами Пирса и исключённого третьего. В какой-то степени всю эту троицу можно расценивать, как эквивалентную друг другу. Некоторые философы даже выводят их один из другого.

Закон Клавия

Очередной закон логики – закон Клавия объединяет отрицание и импликацию (которая обычно выражается формулировкой «если, то»). Этот принцип разработал математик-немец Христофор Клавий, впервые упомянувший его в своей научной работе, посвященной евклидовой «Геометрии». Напомним, что античный философ доказал одну из своих теорем, допустив, что она не верна.
Принцып закона Клафия: если некоторое утверждение является следствием своего отрицания, то оно (данное утверждение) является истинным.

Закон контрапозиции

Этот закон классической логики настаивает на том, что при условии, если некоторая посылка A влечёт за собой некое следствие B, то отрицание данного следствия (иными словами «не B») влечёт отрицание такой посылки (иными словами «не A»). Закон контрапозиции, как и закон двойного отрицания, наибольшее применение получил в математических выражениях.

Закон Пирса

Закон Пирса принято расценивать, как своеобразный аналог сразу нескольких законов классической логики: исключенного третьего и двойного отрицания. Свое название он получил в честь Чарльза Пирса, логика и философа из США.
Закон Пирса сформулирован следующим образом:
P должно быть истинным, если следование Q из P с необходимостью влечёт P. Данный логический принцип принято считать тавтологией классической логики и аналогом законов исключенного третьего и двойного отрицания. Многие философы говорят об эквивалентности всех трех законов.

Правила (законы) де Моргана

Законы де Мо?ргана это такие логические правила, которые посредством логического отрицания объединяют пары логических операций. Свое название они получили в честь Огастеса де Моргана, выдающегося математика из Шотландии. Вкратце законы де Моргана можно представить двумя формулами:

Отрицание дизъюнкции есть не что иное, как конъюнкция отрицаний
Отрицание конъюнкции есть не что иное, как дизъюнкция отрицаний

Правила де Моргана особо распространены в электромеханике, дискретной математике, физике. В информатике они применяются с целью оптимизационных работ с цифровыми схемами через замену логических элементов другими логическими элементами.

Законы деления (дихотомия логики)

Логические законы деления существуют для эффективной систематизации и соответствующей классификации различных предметов или явлений. При этом в делении применяются важнейшие принцыпы:

необходимость соразмерного деления
предметам деления следует друг друга исключать, иными словами они не должны пересекаться между собой
на всех своих этапах деление необходимо производить только по одному основанию
следует исключить скачкообразное деление

При делении объема понятия иногда допускаются ошибки:

• понятие делится в неполном объеме;
• деление чересчур обширно;
• логическая ошибка, возникающая в связи с нарушением правила о необходимости непрерывного деления (ошибка называется «скачок в делении»)

Ниже представлена таблица с формулами основных логичесских законов.

Похожие статьи

 

Please enable JavaScript to view the comments powered by Disqus.

Учебник для студентов юридических вузов и факультетов

1. Закон тождества

Объективный характер и сущность закона тождества. С действием этого закона связано такое коренное свойство правильного мышления, как его определенность.

Что же послужило объективным основанием для возникновения и действия этого закона в мышлении? Как уже отмечалось ранее, одним из фундаментальных свойств окружающего нас мира выступает качественная определенность самих предметов и явлений действительности, отражаемых в мышлении. Это означает, что, несмотря на непрерывно происходящие в них изменения, они до поры до времени остаются теми же самыми, тождественными себе. Например, после долгих лет отлучки мы посетили родные места, где прошло наше детство. Мы видим, что многое вокруг изменилось. И все же мы узнаём свой дом, улицу, школу, родных и близких. Почему? Да потому, что при всех многообразных изменениях они сохранили свой неповторимый облик, то, что делало их данными, а не иными, они не утратили тождества с собой. И даже риторический вопрос Евгения Онегина: «Ужель та самая Татьяна..?» — лишь подчеркивает наличие тождества: конечно, та самая, хотя и прошло столько времени.

Подобную диалектику самой действительности выразил в своих стихах А. Блок:

Идут века, шумит война,

Встает мятеж, горят деревни,

А ты все та ж, моя страна,

В красе заплаканной и древней.

Даже в той парадоксальной ситуации, созданной воображением Льюиса Кэрролла, когда Алиса в течение дня несколько раз сильно меняется — то вдруг вырастает, то уменьшается в размерах, она все же остается той же самой Алисой и не превращается в других обитателей Страны чудес. Иначе повествование о ней было бы невозможным[50].

Но если действительность именно такова, если предметы и явления определенны и эта определенность более или менее длительно сохраняется, то какой будет мысль о них, каким свойством она будет обладать, коль в ней верно отражаются эти предметы и явления? Она будет тоже определенной, тождественной себе.

Вот эту определенность мысли о качественно определенном предмете и отражает формально-логический закон тождества. Честь открытия этого закона принадлежит Аристотелю. Он писал: «…Невозможно что-либо мыслить, если не мыслят что-то одно…»[51].

Правда, Аристотель не дал ему своего названия. Оно появилось в логике позднее. Сам же закон в разные эпохи у разных авторов получал неоднозначное толкование и весьма различные формулировки. Воспользуемся этим обстоятельством и дадим ему следующую формулировку: мысль о качественно определенном предмете, если она соответствует ему, не может не быть определенной, однозначной, тождественной себе.

Отсюда — наименование самого закона: закон тождества. Его наиболее общая формула: «А есть А» или «А = А», где под «А» разумеется всякая мысль вообще.

Закон тождества есть закон функционирования отдельно взятой мысли. Но, как и во всяком законе, в нем так или иначе выражается внутренняя, существенная, необходимая связь, повторяющаяся всегда и всюду при определенных условиях. В данном случае это отношение тождества мысли с самой собой, сколько бы раз она ни появлялась в рассуждении и в какие бы взаимоотношения ни вступала с другими мыслями. Иначе это будет уже другая мысль.

Исторически закон тождества в качестве формально-логического закона явился обобщением практики оперирования понятиями и выражающими их словами или словосочетаниями. И в настоящее время он действует прежде всего в сфере понятий и проявляется уже в процессе их образования. Как известно, любое понятие может быть образовано правильно и неправильно. Если в одно и то же понятие объединяются разнородные элементы, то оно оказывается расплывчатым, смутным, неопределенным, а действительность в нем искажается. Например, так будет в том случае, когда в понятие «мебель» мы включим столы, кастрюльки, ложки и т. д. Если же понятие охватывает лишь такие предметы, которые едины, общи, тождественны в том или ином отношении, то оно будет четким и ясным, будет иметь определенное содержание и определенный объем. Например: мебель — это столы, стулья, шкафы и т. п. Закон тождества обнаруживает свое действие и в процессе использования уже готовых понятий. Если бы в них не было определенности, однозначности, тождественности, если бы они то и дело неуловимо меняли свое содержание и свой объем, то мы попросту не могли бы их применять. Так, лишь зная точное содержание понятия «товар», мы можем твердо, однозначно, категорично ответить, являются ли, например, сапоги товаром или нет: если они произведены для продажи, то это товар, если для себя, то нет.

Если бы понятия не были определенными по своему содержанию и объему, то мы не смогли бы выделять их виды, устанавливать отношения между ними, производить над ними логические операции — определения, деления, обобщения и ограничения.

Действие закона тождества простирается и на суждения. Определенность понятий, из которых они образуются, служит важнейшей предпосылкой их определенности. Но этим действие закона тождества не исчерпывается. Ведь наиболее глубокая сущность суждений — в отражаемых ими связях и отношениях действительности. И если эти связи и отношения определенны, то и суждение, верно отражающее их, не может не быть определенным.

Пожалуй, наиболее рельефно закон тождества проявляется в суждениях типа: «Солнце есть Солнце», «Война есть война» и др., упоминавшихся выше. В них непосредственно раскрывается тождество предмета с самим собой. И такие суждения нередки в практике мышления. Вспомним слова поэта: «Осел останется ослом, хотя осыпь его звездами». Или высказывания других авторов: «Факты есть факты, и по вашему желанию они никуда не исчезнут»; «Прибыль есть прибыль, как бы мала она ни была»; «Джентльмен всегда джентльмен». А вот заголовки из современных газет: «Мастер — он и в глубинке мастер»; «Ложь всегда есть ложь»; «Преступность везде преступность». Вспомним народную мудрость: «Что в лоб, что по лбу»; «Как был дураком, так им и остался» и др.

Разновидностью подобных суждений, выражающих объективное тождество, служат суждения типа: «Отрицательный результат тоже результат»; «Мировой судья есть судья»; «Суров закон, но он закон». Здесь налицо тождество рода и вида (в том смысле, что вид заключает в себе все признаки рода, хотя и не наоборот).

Обобщая, можно сказать, что любое суждение — будь то атрибутивное или реляционное, — фиксируя то или иное тождество свойств предметов или отношений между предметами, является утверждением или отрицанием и в силу этого может быть истинным или ложным. В свою очередь, каждое простое суждение, вступая в связи с другими, образуя конъюнкцию, дизъюнкцию и т. д., сохраняет в них свой определенный, однозначный смысл. Без этого было бы тоже невозможно выяснять значение истинности или ложности сложного суждения, включать его в еще более сложные мыслительные конструкции.

Действие закона тождества распространяется и на обширную область умозаключений. Так, простой категорический силлогизм возможен, в частности, потому, что средний термин, связывающий большую и меньшую посылки, сохраняет в них один и тот же смысл. А больший и меньший термины не только сохраняют свой смысл в посылках и заключении, но если они не распределены в посылках, то не могут быть распределены и в заключении. В противном случае силлогизм оказывается неправильным.

В доказательстве, если оно тоже правильное, закон тождества проявляется в том, что и тезис, и основания сохраняют свою определенность на протяжении всей данной логической процедуры. Без этого доказательство не состоялось бы или было бы неправильным.

Наконец, теория может возникнуть и успешно развиваться, если исходное знание — факты или аксиомы — определенны и сохраняют свой смысл на протяжении более или менее длительного времени. Точно также производное знание — теоремы, принципы, законы — имеет значение постольку, поскольку оно тоже определенно, однозначно, тождественно себе.

Из этого краткого обзора видно, что закон тождества универсален в смысле охвата всех без исключения форм мышления, всякой мысли вообще.

Требования закона тождества и логические ошибки из-за их нарушения. Из объективно действующего в нашем мышлении закона тождества вытекают определенные требования. Это логические нормы, установки, предписания или правила, которые формулируются самими людьми на основе закона и которые необходимо соблюдать, чтобы мышление было правильным, ведущим к истине. Их можно свести к следующим двум.

1. Каждое понятие, суждение и т. д. должны употребляться в одном и том же, определенном смысле и сохранять его в процессе всего рассуждения.

2. Нельзя отождествлять различные мысли и нельзя тождественные мысли принимать за различные.

Требуя определенности, однозначности мысли, закон тождества в то же время направлен против всякой нечеткости, неточности, размытости наших понятий. По Ф. Бэкону, если понятия неотчетливы, то нет ничего прочного в том, что на них построено[52].

В тех случаях, когда требования закона тождества нарушаются, возникают многочисленные логические ошибки. Они называются по-разному: «амфиболия» (двусмысленность, т. е. употребление одного и того же слова-омонима одновременно в,разных смыслах), «смешение понятий», «путаница в понятиях», «подмена одного понятия другим», «подмена тезиса» и т. д.

Аналогичная ситуация нередко возникает во сне. Вот что рассказывал один психолог: «Припоминаю, что однажды я видел себя во сне куда-то едущим: сначала я ехал в пролетке, потом немедленно за этим ехал в санях и еще через мгновение был уже в лодке на какой-то реке, и эта быстрая смена способов передвижения меня нисколько не удивила». Действительно, во сне мы зачастую не сознаем, что это алогичность. Но если мы проснулись и понимаем, что так не бывает, то это значит, что в нашем мышлении действует закон тождества. Ибо если мы едем в пролетке, то это именно пролетка, и она не может быть через мгновение санями или лодкой.

Отождествление нетождественного во сне хорошо описал Л. Толстой в романе «Анна Каренина». Облонский, просыпаясь, вспоминает сонные видения: «Да, как это было? Да! Алабин давал обед в Дармштадте; нет, не в Дармштадте, а что-то американское. Да, но там Дармштадт был в Америке. Да, Алабин давал обед на стеклянных столах, да, — и столы пели: И mio tesoro (мое сокровище), и не II mio tesoro, а что-то лучше, и какие-то маленькие графинчики, и они же женщины». Здесь налицо несколько сбоев мысли о случившемся: Дармштадт не Дармштадт, поющие столы, графинчики-женщины…

Подобная неопределенность мышления возможна и в состоянии бодрствования. Вспомним классический образ Хлестакова в пьесе Н. Гоголя «Ревизор». Сам Гоголь обрисовал его так. Он не в состоянии остановить постоянного внимания на какой-нибудь мысли. Речь его отрывиста, и слова вылетают из уст его совершенно неожиданно. В самой пьесе, нарисовав яркую картину вранья Хлестакова, Гоголь показал, как раздваивается его мысль, теряет определенность и становится непонятной, бессмысленной. Он безбожно путает разных людей — Смирдина с Брамбеусом, Маврушку с посланниками и т. д. А когда, делая предложение дочери городничего Марье Антоновне, он вдруг делает аналогичное предложение его жене Анне Андреевне, та произносит знаменательную фразу: «Но позвольте, я еще не понимаю значения слов». Это верный показатель того, что мышление Хлестакова окончательно запутывается, требования закона тождества не выполняются.

Яркие примеры нелогичного мышления, вызванного нарушениями требований закона тождества — двусмыслицами, неожиданными переосмыслениями слов и т. д., дает Л. Кэрролл в «Приключениях Алисы в Стране чудес». Вот лишь один из них:

«— Совершенно верно, — согласилась Герцогиня. — Фламинго кусаются не хуже горчицы. А мораль отсюда такова: это птицы одного полета!

— Только горчица совсем не птица, — заметила Алиса…

— Кажется, горчица — минерал, — продолжала Алиса задумчиво.

— Конечно, минерал, — подтвердила Герцогиня… — Минерал огромной взрывчатой силы. Из нее делают мины и закладывают при подкопах… А мораль отсюда такова: хорошая мина при плохой игре — самое главное!

— Вспомнила, — сказала вдруг Алиса… — Горчица — это овощ. Правда, на овощ она не похожа — и все-таки это овощ!

— Я совершенно с тобой согласна, — сказала Герцогиня. — А мораль отсюда такова: всякому овощу свое время! Или, хочешь, я это сформулирую попроще: никогда не думай, что ты иная, чем могла бы быть иначе, чем будучи иной в тех случаях, когда иначе нельзя не быть»[53].

Это апофеоз бессмыслицы: мысль Герцогини окончательно запутывается и теряет всякую определенность.

Подобное бывает и в реальной практике мышления. Вот что писал по этому поводу Г. Плеханов. «Иногда людям приходится вести долгие споры просто потому, что они употребляют слова в разных смыслах. Это скучные и бесплодные споры. Но еще несравненно скучнее и еще несравненно бесплоднее такие споры, в которых один человек связывает с данными словами определенное понятие, а у его противника с теми же словами не связывается ровно никаких определенных понятий, вследствие чего он и получает возможность играть ими как ему вздумается»[54].

Иногда подмена понятия, использование одного и того же слова одновременно в разных смыслах осуществляется сознательно — в качестве основы для остроты. Вспомним рекламу: «Мы не в Находке, мы в Москве, но мы находка для вас». Или: «Шли дождь и два студента». Но этим не отрицается, а лишь подтверждается действие закона тождества в нормально протекающем, не парадоксальном мышлении.

Значение закона тождества. Знание закона тождества и его использование в практике мышления имеет принципиальное значение, так как позволяет сознательно и четко отделять правильное рассуждение от неправильного, находить логические ошибки — двусмысленность, подмену понятий и т. д. — в рассуждениях других людей и избегать в своих собственных.

В любой речи — письменной или устной — следует в соответствии с законом тождества добиваться ясности изложения, а она предполагает использование слов и выражений в одном и том же смысле, понятном для других, и в естественных сочетаниях с другими словами.

Очень важно соблюдать требования закона тождества в дискуссиях, спорах и т. д. Чтобы спор не был беспредметным, необходимо всегда точно определить предмет спора и точно выяснить ключевые понятия в нем. Для равнозначных понятий можно и нужно использовать слова-синонимы. Они, как уже отмечалось, обогащают речь. Следует лишь помнить, что синонимия носит относительный характер (слова, являющиеся синонимами в одном отношении, не являются ими в другом). А под видом синонимов иногда употребляются совершенно разные понятия. Если же применяются слова-омонимы, то требуется точно выяснить тот смысл, в котором они в данном случае берутся.

Неоценимо значение требований закона тождества в деятельности юриста. Надо учитывать, что даже в законодательных актах, над которыми, как правило, ведется особенно тщательная работа, нередко встречаются неясности и просто двусмысленности. А это очень опасно, так как неизбежно ведет к различному толкованию одного и того же закона и, следовательно, к его неоднозначному применению.

На требованиях закона тождества основано такое важное следственное действие, как опознание.

В ст. 193 УПК РФ «Предъявление для опознания» говорится, что следователь может предъявить для опознания лицо или предмет свидетелю, потерпевшему, подозреваемому или обвиняемому. Для опознания может быть предъявлен и труп. А далее тщательно раскрывается механизм этой процедуры.

В следственной практике широко используется также идентификация (отождествление). Ее задача — установление тождества тех или иных вещей, людей, документов и т. д., которые до этого мыслились раздельно. Например, идентификация подозреваемого в разных преступлениях, идентификация ножа, которым был ранен или убит человек, и ножа, найденного у подозреваемого. Для этого применяются так называемые «идентификационные свойства». Идентификация живых лиц может производиться на основе их анатомических признаков — роста, строения, пальцевых узоров, по признакам почерка, фотоснимкам и пр. Идентификация вещей — по их следам: на пулях, гильзах и т. п.

Иногда идентификация представляет собой сложнейший процесс с привлечением самых различных специалистов. Вспомним идентификацию останков последнего российского царя Николая II и его семьи, расстрелянных в Екатеринбурге.

В ходе расследования и на самом суде важно выяснить точный смысл, в котором употребляются слова обвиняемым, свидетелем; не подменять их, иначе цель не будет достигнута, а дело приостановлено из-за возникших неясностей. В самом приговоре или решении особенно важны точность понятий, их определенность и однозначность, исключающие всякую недоговоренность, неясность, неточность.

законов мысли | Определение, теории и факты

Законы мысли , традиционно, три фундаментальных закона логики: (1) закон противоречия, (2) закон исключенного среднего (или третьего) и (3) принцип идентичности. Символически эти три закона можно сформулировать следующим образом. (1) Для всех утверждений p невозможно, чтобы оба утверждения p и p были истинными, или: ∼ ( p · ∼ p ), в котором ∼ означает «не» и · означает «и.”(2) Либо p , либо ∼ p должно быть истинным, если между ними нет третьего или среднего истинного утверждения, либо: p ∨ ∼ p , где ∨ означает« или ». (3) Если пропозициональная функция F истинна для отдельной переменной x , то F истинна для x , или: F ( x ) ⊃ F ( x ) , в котором ⊃ означает «формально подразумевает». Другая формулировка принципа идентичности утверждает, что вещь идентична самой себе, или (∀ x ) ( x = x ), где ∀ означает «для каждого»; или просто x — это x .

Аристотель приводил законы противоречия и исключенного третьего в качестве примеров аксиом. Он частично исключил будущие контингенты или заявления о неуверенных будущих событиях из закона исключенного третьего, считая, что (сейчас) не является ни правдой, ни ложью, что завтра будет морское сражение, но что сложное утверждение, что либо будет морское сражение завтра или то, что не будет, — это (сейчас) правда. В эпохальном Principia Mathematica (1910–13) Альфреда Норта Уайтхеда и Бертрана Рассела этот закон встречается скорее как теорема, чем как аксиома.

Доктрина, распространенная среди традиционных логиков, заключалась в том, что законы мышления являются достаточным основанием для всей логики или что все другие принципы логики являются их простым развитием. Закон исключенного среднего и некоторые родственные законы были отвергнуты голландским математиком L.E.J. Брауэр, основоположник математического интуиционизма, и его школа, которые не допускали их использования в математических доказательствах, в которых участвуют все члены бесконечного класса. Брауэр не согласился бы, например, с дизъюнкцией, согласно которой в десятичном разложении π либо встречаются 10 следующих друг за другом семерок, либо нет, так как ни одна из альтернатив неизвестна, но он согласился бы, если бы применил, например, к первые 10 ¹⁰⁰ десятичных цифр, поскольку они в принципе могут быть вычислены.

В 1920 году Ян Лукасевич, ведущий представитель польской логической школы, сформулировал исчисление высказываний, которое имело третью истинностную ценность, ни истину, ни ложь, для будущих контингентов Аристотеля, исчисление, в котором законы противоречия и исключения исключаются. средние оба не удалось. Другие системы вышли за рамки трехзначной логики к многозначной — например, определенные вероятностные логики, имеющие различную степень истинности между истиной и ложью.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас

Logic | Britannica

Объем и основные концепции

Вывод — это управляемый правилами шаг от одного или нескольких предложений, называемых предпосылками, к новому предложению, обычно называемому заключением. Говорят, что правило вывода сохраняет истину, если вывод, полученный в результате применения правила, истинен, когда истинны посылки. Выводы, основанные на правилах сохранения истины, называются дедуктивными, а изучение таких выводов известно как дедуктивная логика.Правило вывода считается действительным или дедуктивно действительным, если оно обязательно сохраняет истину. То есть в любом мыслимом случае, в котором посылки истинны, вывод, сделанный с помощью правила вывода, также будет истинным. Выводы, основанные на действительных правилах вывода, также считаются действительными.

Логика в узком смысле эквивалентна дедуктивной логике. По определению, такое рассуждение не может дать никакой информации (в форме заключения), которая еще не содержится в предпосылках.В более широком смысле, близком к обычному использованию, логика также включает изучение умозаключений, которые могут привести к заключениям, содержащим действительно новую информацию. Такие выводы называются амплиативными или индуктивными, а их формальное изучение известно как индуктивная логика. Они проиллюстрированы выводами, сделанными умными детективами, такими как вымышленный Шерлок Холмс.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Контраст между дедуктивными и амплиативными выводами можно проиллюстрировать на следующих примерах.Из предпосылки «кто-то всем завидует» можно обоснованно сделать вывод, что «все кому-то завидуют». Не существует мыслимого случая, в котором посылка этого вывода истинна, а вывод ложен. Однако, когда судмедэксперт делает вывод из определенных свойств набора человеческих костей о приблизительном возрасте, росте и различных других характеристиках умершего человека, его аргументация является усиленной, потому что, по крайней мере, можно предположить, что сделанные им выводы ошиблись.

В еще более узком смысле логика ограничивается изучением выводов, которые зависят только от определенных логических концепций, выражаемых так называемыми «логическими константами» (логику в этом смысле иногда называют элементарной логикой). Наиболее важные логические константы — это кванторы, пропозициональные связки и идентичность. Квантификаторы являются формальными аналогами английских фраз, таких как «there is…» или «there exists…», а также «for every…» и «for all…». Они используются в формальных выражениях, таких как (∃ x ) (читается как «есть человек, назовите его x , так что для x верно то, что…») и (∀ y ) (читается как «для каждого человека, назовите его y , это верно для и , что… »).Основные пропозициональные связки в английском языке аппроксимируются «not» (~), «and» (&), «or» (∨) и «if… then…» (⊃). Идентичность, представленная символом ≡, обычно передается на английском языке как «… является…» или «… идентично…». Два приведенных выше примера предложения могут быть выражены как (1) и (2) соответственно:

(1) (∃ x ) (∀ y ) ( x завидует y )

(2) (∀ y ) (∃ x ) ( x завидует y )

Способ, которым различные логические константы в предложении связаны друг с другом, известен как логическая форма предложения.Логическую форму можно также рассматривать как результат замены всех нелогических понятий в предложении логическими константами или общими логическими символами, известными как переменные. Например, заменяя реляционное выражение «a завидует b» на «E (a, b)» в (1) и (2) выше, получаем (3) и (4) соответственно:

(3) (∃ x ) (∀ y ) E ( x , y )

(4) (∀ y ) (∃ x ) E ( x , y )

Формулы в (3) и (4) выше являются явным представлением логических форм соответствующих английских предложений.Изучение отношений между такими неинтерпретируемыми формулами называется формальной логикой.

Следует отметить, что логические константы имеют такое же значение в логических формулах, как (3) и (4), как и в предложениях, которые также содержат нелогические понятия, такие как (1) и (2). Логическая формула, переменные которой заменены нелогическими понятиями (значениями или референтами), называется «интерпретируемым» утверждением или просто «интерпретацией». Один из способов выразить обоснованность вывода от (3) к (4) — сказать, что соответствующий вывод от предложения, подобного (1), к предложению, подобному (2), будет действительным для всех возможных интерпретаций (3) и (4).

Правильные логические выводы становятся возможными благодаря тому факту, что логические константы в сочетании с нелогическими концепциями позволяют утверждению представлять реальность. Действительно, эту репрезентативную функцию можно считать их самой фундаментальной особенностью. Предложение G, например, может быть правильно выведено из другого предложения F, когда все сценарии, представленные F — сценарии, в которых F истинно, — также сценарии, представленные G — сценарии, в которых G истинно. В этом смысле (2) можно обоснованно вывести из (1), потому что все сценарии, в которых верно то, что кто-то завидует всем, также являются сценариями, в которых верно то, что всем завидует по крайней мере один человек.

Утверждение считается логически истинным, если оно истинно во всех возможных сценариях или «возможных мирах». Утверждение противоречиво, если оно ложно во всех возможных мирах. Таким образом, еще один способ выразить обоснованность вывода из F в G — это сказать, что условное утверждение «Если F, то G» (F ⊃ G) логически истинно.

Однако не все философы принимают эти объяснения логической достоверности. Для некоторых из них логические истины — это просто самые общие истины о реальном мире.Для других это истина об определенной неуловимой части реального мира, содержащей абстрактные сущности, подобные логическим формам.

Помимо дедуктивной логики, существуют другие ветви логики, изучающие выводы, основанные на таких понятиях, как знание этого (эпистемическая логика), вера в это (доксастическая логика), время (временная логика) и моральное обязательство (деонтическая логика), среди которых другие. Эти области иногда называют философской логикой или прикладной логикой. Некоторые математики и философы считают теорию множеств, изучающую отношения принадлежности между множествами, еще одной ветвью логики.

Три закона логики — Урок гуманитарных наук [видео 2021]

Закон идентичности

Закон идентичности гласит, что если утверждение было определено как истинное, то утверждение истинно. Проще говоря, в нем говорится, что «X есть X». Например, если я говорю, что «идет снег», и это правда, то это утверждение должно быть правдой. Если мы посмотрим на закон идентичности в более общем плане, он говорит, что каждая существующая вещь состоит из своих собственных особых характеристик, которые являются частью того, чем она является.

Когда вы применяете это к логике, закон тождества по существу означает, что все есть само по себе и не может быть чем-то другим. Снег не может быть облаками, а вода не может быть полюсом. Каждая вещь — это нечто особенное, имеющее определенную индивидуальность. Поэтому, когда я говорю, что идет снег, снег относится к определенному событию. Учитывая, что «снегопад» относится к определенной вещи, если я сделаю это утверждение, когда на самом деле идет снег, то это должно быть истинное утверждение.

Закон непротиворечия

Согласно закону непротиворечивости , утверждение типа «идет снег» не может быть одновременно истинным и ложным.Проще говоря, в нем говорится, что «X не является X». Это означает, что в одном и том же месте не может быть и снега, и не снега в один и тот же период времени. Другими словами, ничто истинное не может противоречить самому себе. Закон непротиворечия очень важен. Без этого мы не смогли бы мыслить рационально.

Закон исключенного среднего

Третий и последний закон — это закон исключенного среднего . Согласно этому закону такое утверждение, как «идет снег», должно быть либо правдой, либо ложью.Либо идет снег, либо нет; других альтернатив нет. Проще говоря, это «либо X, либо не X». Согласно этому закону, реальные противоречия не могут существовать; противоречия являются результатом недостатка данных или языковых ограничений. Поэтому, когда нам предлагают зеленый объект и спрашивают, является ли объект синим или желтым, мы должны предположить, что объект не желтый или синий, а нечто совершенно иное: зеленый.

Резюме урока

Давайте сделаем пару мгновений, чтобы повторить то, что мы узнали о законах логики.

Есть три закона, на которых основана вся логика, и они приписаны Аристотелю. Эти законы суть закон тождества, закон непротиворечивости и закон исключенного третьего. Согласно закону идентичности , если утверждение верно, то оно должно быть правдой. Закон о непротиворечивости гласит, что утверждение не может быть истинным и ложным одновременно в одной и той же манере. Наконец, закон исключенной середины гласит, что утверждение должно быть либо истинным, либо ложным.

Каковы три закона логики?

Дж. П. Морленд —

Есть три основных закона логики. Предположим, что P — это любое ориентировочное предложение, скажем: «Идет дождь».

Закон тождества: P — это P.
Закон непротиворечивости: P не является P.
Закон исключенного третьего: Либо П, либо не П.

Закон идентичности гласит, что если утверждение типа «идет дождь» верно, то это утверждение верно.В более общем плане он говорит, что утверждение P — это то же самое, что и само по себе, и оно отличается от всего остального. Применительно ко всей реальности закон идентичности гласит, что все есть само, а не что-то еще.

Закон непротиворечивости гласит, что такое утверждение, как «идет дождь», не может быть одновременно истинным и ложным в одном и том же смысле. Конечно, в Миссури может идти дождь, а в Аризоне — нет, но принцип гласит, что дождь не может идти и не идти одновременно в одном и том же месте.

Закон исключенного третьего гласит, что такое утверждение, как «идет дождь», является либо истинным, либо ложным. Другой альтернативы нет.

Эти фундаментальные законы являются истинными принципами, управляющими реальностью и мышлением, и принимаются Писанием. Некоторые заявляют, что это произвольные западные конструкции, но это неверно. Основные законы логики управляют всей реальностью и мыслью и известны как истинные по крайней мере по двум причинам: (1) они интуитивно очевидны и самоочевидны. Как только кто-то поймет основной закон логики (см. Ниже), он сможет увидеть, что это правда.(2) Те, кто их отрицают, используют эти принципы в своем отрицании, демонстрируя, что эти законы неизбежны и что отрицать их — самооправдание.

Основные законы логики не являются ни произвольными изобретениями Бога, ни принципами, которые существуют полностью вне Его бытия. Очевидно, что законы логики не похожи на законы природы. Бог может нарушить последнее (например, приостановить гравитацию), но Он не может нарушить первое. Эти законы коренятся в самой природе Бога. Действительно, некоторые ученые считают, что отрывок «Вначале было Слово [логос]» (Иоанна 1: 1) точно переведен: «В начале была Логика (божественный, разумный разум).«Например, даже Бог не может существовать и не существовать одновременно, и даже Бог не может обоснованно полагать, что красный — это цвет, а красный — не цвет. Когда люди говорят, что Богу не нужно вести себя «логически», они используют этот термин в широком смысле, чтобы обозначить «разумные вещи с моей точки зрения». Часто Бог действует не так, как люди понимают или судят так, как они поступили бы в данных обстоятельствах. Но Бог никогда не поступает нелогично в собственном смысле слова. Он не нарушает ни в своем существе, ни в мыслях фундаментальных законов логики.

Аристотель: логика

Аристотель: логика

Аристотель: логические методы

Самый большой и влиятельный из учеников Платона был Аристотель , который основал свою школу в Афинах. Хотя его писательская карьера, вероятно, началась с создания квазиплатонических диалогов, ни один из них не сохранился. Напротив, наши знания доктрин Аристотеля должны быть получены из сжатых эллиптических работ, которые могли быть конспектами лекций его преподавания в лицее.Хотя эти тексты не предназначены для публикации, они раскрывают блестящий ум, работающий над множеством разнообразных тем.

С философской точки зрения работы Аристотеля отражают его постепенный отход от учения Платона и принятие нового подхода. В отличие от Платона, который восхищался абстрактным мышлением о сверхчувственном царстве форм, Аристотель был в высшей степени конкретным и практичным, в значительной степени полагаясь на чувственное наблюдение в качестве отправной точки для философских размышлений.Заинтересовавшись всеми областями человеческих знаний о мире, Аристотель стремился объединить их все в единую систему мышления. путем разработки общей методологии, которая будет одинаково хорошо служить процедурой изучения любой дисциплины.

Таким образом, для Аристотеля логика — это инструмент («органон»), с помощью которого мы приходим к познанию чего-либо. Он предложил в качестве формальных правил правильного рассуждения основные принципы категорическая логика, которая была повсеместно принята западными философами до XIX века.Эта система мышления рассматривает утверждения в форме субъект-предикат как первичные выражения истины, в которых показано, что черты или свойства присущи отдельным субстанциям. Таким образом, в каждой дисциплине человеческого знания мы стремимся установить, что у вещей того или иного вида есть особенности определенного вида.

Далее Аристотель предположил, что эта логическая схема точно отражает истинную природу реальность. Мысль, язык и реальность изоморфны, поэтому внимательное рассмотрение того, что мы говорим, может помочь нам понять, каковы вещи на самом деле.Начиная с простых описаний конкретных вещей, мы можем в конечном итоге собрать нашу информацию, чтобы достичь всеобъемлющего представления о мире.

Применение категорий

Первой книгой в собрании логических сочинений Аристотеля является Категории , анализ предсказаний в целом. Он начинается с различия между тремя способами, которыми значения различных употреблений предиката могут быть связаны друг с другом: омонимия, синонимия и паронимия (в некоторых переводах «двусмысленный», «однозначный» и «производный»).Одноименные употребления предиката имеют совершенно разные объяснения, например, «Со всеми этими деньгами она действительно загружена» и «После всего, что ей пришлось выпить, она действительно загружена». Синонимичные употребления имеют точно такое же значение, как в словах «Коровы — млекопитающие» и «Дельфины — млекопитающие». Паронимические атрибуции имеют различные, но связанные смыслы, например, «Он здоров» и «Его цвет лица здоровый». ( Категории 1) В каждом случае важно понимать, как это использование предиката соотносится с другими его применениями.

До тех пор, пока мы четко понимаем, какое использование мы делаем в каждом конкретном случае, Аристотель предлагал разработать описания отдельных вещей, которые приписывают каждому предикату. (или категорий) десяти разных видов. Вещество является наиболее важным из этих десяти, так как оно описывает вещь с точки зрения того, чем она является на самом деле. Для Аристотеля первичная субстанция — это просто индивидуальная вещь, которую нельзя предсказать ни на что другое. Но вторичные субстанции предсказуемы, поскольку они включают виды и роды, к которым принадлежит индивидуальная вещь.Таким образом, приписывание субстанции в этом вторичном смысле устанавливает сущность каждой отдельной вещи.

Остальные девять категорий — количество, качество, относительный, где, когда, занимать положение, иметь, действовать и подвергаться влиянию — описывают особенности, которые отличают эту индивидуальную субстанцию ​​от других того же вида; они допускают степени, и их противоположности могут принадлежать к одному и тому же. ( Категории 4) При использовании в комбинации десять видов предикатов могут дать исчерпывающее представление о том, что собой представляет каждая отдельная вещь.Таким образом, например: Хлоя — собака, которая весит сорок фунтов, красновато-коричневая и была одной из семи собак помета. Она в моей квартире в 7:44 утра. 3 июня 1997 г. она лежала на диване в синем воротничке, лаяла на белку и ее гладили. Аристотель полагал, что все, что истинно в отношении любой индивидуальной субстанции, в принципе можно было сказать об этом одним из этих десяти способов.

Природа истины

Еще одна из логических работ Аристотеля , On Interpretation , рассматривает использование предикатов в сочетании с подлежащими для формирования предложения или утверждения, каждое из которых истинно или ложно.Обычно мы определяем истинность предложения, ссылаясь на наш опыт реальности, которую оно передает, но Аристотель признавал, что при определенных обстоятельствах возникают особые трудности.

Хотя мы допускаем (и часто можем даже обнаружить) истинность или ложность утверждений о прошлых и настоящих событиях, предположения о будущем кажутся проблематичными. Если суждение о завтрашнем дне истинно (или ложно) сегодня, то будущее событие, которое оно описывает, обязательно произойдет (или не произойдет); но если такое предположение не является ни истинным, ни ложным, то будущего вообще нет.Решение Аристотеля состояло в том, чтобы утверждать, что дизъюнкция обязательно истинна сегодня, даже если ни одна из ее дизъюнкций не верна. Таким образом, необходимо, чтобы завтрашнее событие либо произошло, либо нет, но не обязательно, чтобы оно произошло, и не обязательно, чтобы оно не произошло. (Об интерпретации 9)

Трактовка Аристотелем этой конкретной проблемы, как и его более общая попытка разобраться в природе взаимосвязи между необходимость и непредвиденные обстоятельства в В интерпретации 12-13 усложняется предположение, что структура логики моделирует природу реальности.Он должен попытаться объяснить не только то, как мы говорим, но и то, каким должен быть мир.

Демонстрационная наука

Наконец, в Prior Analytics и Posterior Analytics , Аристотель представил подробный отчет о демонстративных рассуждениях, необходимых для обоснования теоретические знания. Используя математику в качестве модели, Аристотель предположил, что все такие знания должны быть получены из того, что уже известно. Таким образом, в процессе рассуждений с помощью силлогизма используется формальное определение термина. обоснованность, позволяющая выводить новые истины из установленных принципов.Цель состоит в том, чтобы объяснить, почему все происходит именно так, исключительно на основании того, что мы уже знаем.

Чтобы достичь подлинной необходимости, эта доказательная наука должна быть сосредоточена на сущности, а не случайности вещей, о том, что «верно для любого случая как такового», а не о том, что «верно для каждого случая на самом деле». Недостаточно знать, что сегодня шел дождь; мы должны быть в состоянии выяснить общие метеорологические условия, при которых дождь неизбежен.Когда мы рассуждаем из необходимых универсальных и утвердительные суждения о существенных особенностях вещей, предполагающие как можно меньше, результирующая совокупность знаний действительно заслуживает названия науки.

Четыре причины

Применяя принципы, разработанные в его логических трактатах, Аристотель предложил общее описание действия отдельных веществ в мире природы. Он провел существенное различие между вещами двух видов: теми, которые движутся только тогда, когда их движет что-то еще, и теми, которые способны двигаться сами.В отдельных трактатах Аристотель не только предлагал правильное описание вещей каждого вида, но также пытался объяснить, почему они действуют именно так.

Аристотель рассматривал тела и их движение, производимое извне, в Физика . Три важных различия определяют форму этого обсуждения физической науки. Во-первых, он с самого начала признал, что из-за различий в их происхождении нам, возможно, придется предложить разные объяснения функций естественных вещей и функций артефактов.Во-вторых, он настаивал на том, чтобы мы четко различали основной материал и форму, которые вместе составляют природу любой индивидуальной вещи. Наконец, Аристотель подчеркивал разницу между вещами такими, какие они есть, и вещами, рассматриваемыми в свете их цели или цели.

Вооружившись этими различиями, Аристотель предложил в Physics II, 3 что мы используем четыре очень разных типа объяснительных принципов {Gk. αιτιον [aition]} на вопрос, почему вещь есть, четыре причины:

Материальная причина — это основной материал, из которого сделана вещь.Материальная причина дома, например, будет включать дерево, металл, стекло и другие строительные материалы, использованные при его строительстве. Все эти вещи относятся к объяснению дома, потому что он не мог бы существовать, если бы они не присутствовали в его составе.

Формальное дело {Gk. ειδος [эйдос]} — это образец или сущность, в соответствии с которыми собираются эти материалы. Таким образом, формальной причиной нашего образцового дома будет то, что изображено на чертеже его дизайна.Это тоже часть объяснения дома, поскольку его материалы были бы всего лишь грудой обломков (или другим домом), если бы они не были собраны таким образом.

Эффективная причина — это агент или сила, непосредственно ответственная за объединение этой материи и этой формы в производстве вещи. Таким образом, эффективная причина дома будет включать плотников, каменщиков, сантехников и других рабочих, которые использовали эти материалы для строительства дома в соответствии с планом его строительства.Ясно, что без их вклада дом не был бы таким, какой он есть.

Наконец, окончательная причина {Gk. τελος [télos]} — это цель или цель, для которой существует вещь, поэтому конечной целью нашего дома будет предоставление убежища людям. Это часть объяснения существования дома, потому что он никогда бы не был построен, если бы кто-то не нуждался в нем как в жилом доме.

Причины всех четырех видов являются необходимыми элементами в любом адекватном объяснении существования и природы вещи, считал Аристотель, поскольку отсутствие или изменение любого из них привело бы к существованию чего-то иного.Более того, объяснение, включающее все четыре причины, полностью отражает значение и реальность самой вещи.

Появление случая

Обратите внимание, что четыре причины больше подходят для артефактов, чем для природных объектов. Возникновение современной науки стало прямым результатом отказа, в частности, от аристотелевского представления о конечных причинах. Тем не менее, эта схема настолько хорошо работает с артефактами, что мы часто приписываем какую-то цель даже кажущимся бессмысленным событиям в мире природы.

Во многих приложениях формальные, эффективные и конечные причины, как правило, объединяются в одно существо, которое проектирует и строит вещь для определенной цели. Таким образом, фундаментальное различие в аристотелевском мире оказывается между инертной материей, с одной стороны, и разумным действием, с другой. Как мы вскоре увидим, это дает естественное объяснение функций одушевленных природных организмов.

Что касается вещей, которые, кажется, возникают случайно, Аристотель утверждал, что, поскольку целенаправленное происхождение, описываемое четырьмя причинами, является нормальным порядком в мире, эти случаи должны быть либо вещами, у которых должна была быть какая-то причина, но которой так и не было, либо (что более вероятно) вещами, у которых действительно есть причины, о которых мы просто не осознаем.Он считал, что мастерство, очевидное при изготовлении артефактов, свидетельствует о целенаправленном характере природы, и оно разделяет ту же необходимость, даже если мы иногда игнорируем ее внутренние операции. ( Физика II, 8)

Хотя мне было бы трудно найти окончательную причину существования комара, который сейчас кусает меня, например, Аристотель предположил, что в конечном итоге должно быть какое-то объяснение его нынешнему существованию и активности.Многие поколения западных философов, особенно те, кто занимался примирением христианской доктрины с философией, открыто защищали бы аналогичную точку зрения.

Закон исключенного среднего

«Вселенная, — говорит Литтон Стрейчи в своей книге« Выдающиеся викторианцы », — полна законов — Закона Тяготения, Закона Исключенного Среднего и многих других». Сейчас мало кто будет спорить с его основным утверждением, но многие ли могут сослаться на Закон исключенного среднего? Как ни странно, это имеет какое-то отношение к метеорологии.

Рассматриваемый принцип является философской концепцией наравне с Парадоксом Рассела и Бритвой Оккама. Последнее, как известно читателям Weather Eye, является Entia non sunt multi-plicanda praeter need itatem: «Не следует предполагать, что существует больше вещей, чем это абсолютно необходимо» — здравый совет, сделанный Вильгельмом Оккамом в 14 веке. С другой стороны, парадокс касается парикмахера. Идиосинкразический парикмахер Рассела зарублен и бреет мужчину тогда и только тогда, когда этот мужчина не бреет себя.Но возникает вопрос: а кто бреет парикмахера? Если он бреется, значит, он этого не делает; но если он не бреется, то, по определению, он это делает. Так он и делает, и одновременно — нет.

Парадокс Рассела, как оказалось, является явным нарушением Закона Исключенного Середина. Упомянутый закон, по-видимому, является одним из трех краеугольных камней аристотелевской логики, призванным заставить нас мыслить более ясно. В нем говорится, что каждое предложение должно быть либо истинным, либо ложным, что не существует золотой середины.Например, типичная роза либо красная, либо не красная; он не может быть красным и не красным.

Но некоторые прогнозы погоды, можно было бы возразить, предполагают еще одно нарушение закона. Согласно Аристотелю и его друзьям, прогноз должен быть либо верным, либо неверным; он не может быть одновременно правильным и неправильным.Но это может быть не так.

На самом деле, полный прогноз погоды редко бывает абсолютно верным, и очень редко полностью неверным. Прогноз, который один человек воспринимал как «хороший», потому что он был верен в том, что его волновало — например, ветер или температура — могло оказаться ошибкой для другого человека, у которого другие интересы. Моряк может мало заботиться о морозе, который беспокоит садоводов, но для него может быть вопросом жизни и смерти своевременное предупреждение о шторме.И предположим, что в определенном месте прогнозируется дождь, и выпадает всего одна капля; для метеоролога прогноз верен — но подходит ли он человеку, который без надобности носит зонт в город?

Как говорит Гамлет: «Горацио, на небе и на земле больше, чем мечтает твоя философия».

Логика Аристотеля

Раздел V

ОБ ЭТОЙ ТЕОРИИ, РАССМАТРИВАЕМЫЙ КАК ДВИГАТЕЛЬ НАУКА

Медленный прогресс полезных знаний, на протяжении многих веков, когда силлогистическое искусство культивировалось как единственный путеводитель по науке и ее быстрый прогресс с тех пор, как это искусство вышло из употребления, предложить презумпцию против этого; и эта презумпция подкрепляется ребячество примеров, которые всегда приводились, чтобы проиллюстрировать его правила.

Кажется, у древних было слишком много понятий, как о силе разумной силы в человеке, так и об искусстве силлогизм как его проводник. Простые рассуждения могут увести нас, но очень мало большинство предметов. При правильном наблюдении и проведенных экспериментах запас человеческие знания могут расширяться без конца; но сила рассуждений в одиночку, с энергией применявшейся в течение долгой жизни, только носил бы человека как лошадь на мельнице, которая упорно трудится, но не продвигается.Там есть действительно, исключение из этого наблюдения в математических науках. В количественные отношения так разнообразны и так поддаются точному измерению, что по этому поводу может быть сформирована длинная цепочка точных рассуждений, и выводы сделаны, очень далекие от первых принципов. Именно в этом науке и тем, кто от нее зависит, торжествует сила рассуждения; в остальном его трофеи незначительны. Если кто в этом сомневается, пусть по любому предмету, не связанному с математикой, он приводит цепочку рассуждений некоторой длины, ведущей к выводу, который без этой цепочки рассуждений никогда бы не попал в поле зрения человека.Каждый мужчина знаком с математика может произвести тысячи таких цепочек рассуждений. Я не говорю что ничего подобного не может быть произведено в других науках; но я считаю, что их мало, и найти нелегко; и что, если они найдутся, то не будет в предметах что может быть выражено категоричными предложениями, к которым только теория фигура и режим расширяется.

В вопросах, на которые распространяется эта теория, здравомыслящий человек, умеющий различать разные вещи, умеющий избегать ловушки двусмысленных слов, и кто умеренно в таких делах, сразу видит все, что можно вывести из таких предпосылок, или обнаруживает, что есть это всего лишь очень короткий шаг к заключению.

Когда сила рассуждения так слаба из-за природы, особенно в предметах, к которым эта теория может быть применена, это было бы ожидать от него больших эффектов неразумно. И поэтому мы видим причину, по которой примеры, приведенные для иллюстрации наиболее изобретательными логиками, скорее склонны к презрению.

Если следует подумать, что силлогистическое искусство может быть полезным двигателем в математике, в которой чистое рассуждение имеет широкие возможности: во-первых, можно заметить, что факты неблагоприятны для этого мнение: Ибо не похоже, чтобы Евклид, или Аполлоний, или Архимед, или Гюйгенс или Ньютон когда-либо меньше всего использовали это искусство; и я даже из мнение, что его нельзя использовать в математике.Я бы не хотел опрометчиво продвигать это, поскольку Аристотель сказал, что большинство математиков рассуждают на первом рисунке. Он так подумал, что только первая фигура дает универсальные и утвердительные выводы, а выводы математика обычно бывает такого рода. Но следует отметить, что предложения математики не являются категориальными предложениями, состоящими из одного подлежащее и одно сказуемое. Они выражают некоторую связь, которую несет одна величина. к другому, а на счету должно быть три срока.Сравниваемые количества составляют два, а отношение между ними — третье. Теперь к таким предложениям мы не можем ни применять правила, касающиеся преобразования предложений, ни могут ли они войти в силлогизм любой из фигур или ладов. Мы наблюдали раньше, что это преобразование, A больше, чем B , поэтому B является меньше, чем A , не подпадает под правила преобразования, установленные Аристотель или логики; и теперь мы добавляем, что это простое рассуждение, A есть равно B, а B — C , поэтому A равно C , не может быть приведен в любой силлогизм по фигуре и манере.Действительно, есть силлогизмы, в которые могут входить математические предложения, о которых мы поговорим позже: но они не имеют ничего общего с системой рисунка и моды.

Когда мы выходим без круга математических наук, я не знаю ничего, в чем, кажется, так много демонстрация как в той части логики, которая рассматривает фигуры и способы силлогизм; но несколько сделанных нами замечаний показывают, что в нем есть некоторые слабые места; и, кроме того, эту систему нельзя использовать в качестве двигателя для самосовершенствования.

Компас силлогистической системы, как двигатель науки, может быть обнаружен при кратком и общем обзоре сделанный вывод и аргумент, использованный для его доказательства, в каждом из трех цифры.

На первом рисунке вывод подтверждает или отрицает что-то от определенного вида или человека; и аргумент докажите, что вывод таков, То же самое может быть подтверждено или опровергнуто всего рода, к которому принадлежит этот вид или особь .

На втором рисунке вывод: Что некоторые виды или особи не принадлежат к такому роду; и аргумент: Что некоторый атрибут, общий для всего рода, не принадлежит этому виду или особи .

На третьем рисунке вывод: Что такой атрибут принадлежит части рода; и аргумент: Это рассматриваемый атрибут принадлежит виду или особи, которая является частью этот род.

Я понимаю, что в этом кратком обзоре каждый вывод, который подпадает под компас трех фигур, а также средство доказательства, постигается.Правила всех фигур могут быть легко выводил из него; и кажется, что есть только один принцип рассуждения во всех трех; так что не странно, что силлогизм одной фигуры должны быть сведены к одному из другого рисунка.

Общий принцип, в котором все заканчивается, и каждый категорический силлогизм является лишь частным заявка, is this, То, что утверждается или отрицается в отношении всего рода, может быть подтвержденным или опровергнутым в отношении всех видов и лиц, принадлежащих к нему Это это действительно принцип несомненной уверенности, но не большой глубины.Аристотель и все логики считают это аксиомой или первым принципом, из которого силлогистическая система как бы берет свое начало; и после утомительного плавания и больших затрат на демонстрацию, наконец, он приземляется в этом принципе, как его окончательный вывод.

«O curas hominum! O Quant est in ребус бессмысленный! »

Раздел VI. НА МОДАЛЬНОМ СИЛЛОГИЗМЫ

Категорические предложения, помимо их количества и качества, имеют еще одну привязанность: которые они делятся на чистый и модальный .В чистом суждение, сказуемое почти не подтверждается или отрицается в отношении подлежащего; но в модальное предложение, утверждение или отрицание модифицируется, будучи объявлено необходимым , или условным , или невозможным . Эти четыре модуса наблюдал Аристотель, из которых он назвал предложение модальное. Его истинные ученики утверждают, что все это режимы, которые могут повлиять на утверждение или отрицание, и что перечисление полный.Другие утверждают, что это перечисление неполное; и что, когда утверждение или отрицание считается определенным или неопределенным, вероятным или маловероятно, это делает модальное предложение, по крайней мере, четыре способа Аристотель. Мы не будем вдаваться в этот спор, но отметим, что эпитеты чистого и модального применяются также к силлогизмам что касается предложений. Чистый силлогизм — это то, в котором обе посылки чисты. предложения. Модальный силлогизм — это то, в котором любая из посылок является модальное предложение.

Силлогизмы, о которых мы уже так много говорили, — это только те, которые чисты, а также категоричный. Но если учесть, что на всех рисунках и в режимах силлогизм может иметь одну модальную предпосылку любого из четырех модусов, в то время как другой чист, или он может иметь обе предпосылки модально, и что они могут быть одним из одного и того же режима или разных режимов, какое огромное разнообразие возникает из всех этих комбинации? Теперь дело логика показать, как заключение затрагивается во всем этом разнообразии случаев.Аристотель сделал это в своем первом Аналитика с огромным трудом; и не покажется странным, что когда он использовал только четыре главы при обсуждении ста девяноста двух режимов, истинных и ложных, чистых силлогизмов, он должен использовать пятнадцать модальных силлогизмы.

Я очень готов извиниться за то, чтобы войти в эту великую ветвь логики, тем, что суждение и пример тех, кого нельзя обвинить ни в неуважении до Аристотеля или с низким уважением к силлогистическому искусству.

Кекерманн, знаменитый профессор дантисканца, который всю жизнь преподавал и писал логику, в своей огромной системе фолио этой науки, опубликованной год 1600, называет доктрина модалов crux Logicorum . Что касается схоластические врачи, среди которых была такая пословица, De modali non gustabit asinus , он считает очень сомнительным, пытали ли они больше всего модальных силлогизмы, или подвергались их пыткам. Но эти раздражительные гении, говорит он, сделали эту доктрину настолько тернистой, что ее лучше растерзать. штук, чем придать им прочность.Он желает, чтобы было соблюдено, что учение модальных окон адаптирован к греческому языку. Модальные условия были часто использовались греками в их диспутах, и по этой причине так полностью обработан Аристотелем; но в диспутах на латинском языке вы вряд ли когда-нибудь встретимся с ними. Я также не помню, из всего моего опыта, говорит он, чтобы увидеть любого человека, которому грозит помешательство в ссоре, из-за его незнания модальных окон.

Этот автор, однако, из уважения к Аристотелю, довольно полно трактует модальные предложения, показывая, как различать их подлежащее и сказуемое, их количество и качество.Но модальный силлогизм он полностью игнорирует.

Людовикус Вивес, о котором я упоминаю, не как приверженец Аристотеля, а по собственному усмотрению. суждение и обучение, считает, что учение о модальных окнах должно быть изгнано вне логики и переведены в грамматику; и что, если грамматика греческого язык был внесен в систему во времена Аристотеля, этот самый острый философ сэкономил бы тот огромный труд, который он вложил в эту тему.

Бургерсдайк, перечислив пять классов модальных силлогизмов, замечает, что они требуют многие правила и предостережения, которыми старательно придерживался Аристотель; но это, как их использование невелико, а их правила сложны, он считает, что это не стоит пока вступать в их обсуждение; рекомендуя тем, кто хотел бы понять их, самый ученый пересказ Иоганна Монлориуса на первая книга Первой аналитики.

Все писатели логики двести лет назад, попавшие в мои руки, прошел мимо правил модальных силлогизмов с минимальной церемонией. Чтобы эта великая ветвь доктрины силлогизмов, которой усердно занимаются Аристотель впал в пренебрежение, если не презирать, хотя учение о чистом силлогизмы продолжали пользоваться большим уважением. Под влиянием этих властей я пусть это учение покоится с миром, не причиняя ни малейшего беспокойства его прах.

.