Работы пифагора список: Пифагор

Содержание

Пифагор — великий древне-греческий учёный

Пифагор — великий древнегреческий учёный.

Лабынцева Татьяна Сергеевна

11 класс

Номинация «Великие математики»

МКОУ «Парфёновская СОШ»

Глазунова Татьяна Ивановна

план

Строки из биографии Пифагора.
Основы пифагоризма.
Числа и формы.
Симметричные геометрические тела
Пифагорейская астрономия
Музыка и математика
Символические афоризмы Пифагора
Выводы

Пифагор Самосский 570 – 496г.г. до н. э.

Мнесарх – отец

Пифарис – мать

Пифагор родился на острове Самос, расположенном в Эгейском море.

Много странных легенд дошло до наших дней о рождении Пифагора. Некоторые из них утверждают, что он не был обычным человеком, а был одним из богов , принявших человеческий облик для того , чтобы войти в мир и учить человеческую расу.

Пифагор – был первым человеком, который назвал себя философом.

До него умные люди звали себя мудрецами.

Философ – человек, который пытается найти, выяснить.
Мудрец – человек, который знает.

По сохранившимся преданиям,

Пифагор много путешествовал:

жил в Египте, Вавилоне, побывал даже в далёкой Индии.

Потом он поселился на юге нынешней Италии, где основал

общество философов – пифагорейский союз

Пифагор составил подробный список табу для членов своего ордена

Вот некоторые из них:

делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться;
не делай никогда того, что не знаешь, но научись всему, что следует знать;
не пренебрегай здоровьем своего тела;
приучайся жить просто и без роскоши.

Основы Пифагоризма

Изучение геометрии, музыки и астрономии существенно для понимания Бога, человека или Природы.
Умеренность во всех вещах.
Поедание мяса затемняет умственные способности.
Противился хирургии во всех её проявлениях.
Дружба является самым истинным и почти совершенным из всех человеческих отношений
Вера в переселение душ.
Всё в природе разделено на три части. Пифагор говорил: «Узрите треугольник и проблема на две трети решена»

Числа и формы

Центральное место в философии воспитанников и приверженцев Пифагора занимали числа:

«Где нет числа и меры — там хаос и химеры»,
«Самое мудрое – это число»,
«Числа управляют миром».

Поэтому многие считают Пифагора отцом нумерации – сложной, окутанной тайной науки, описывающей с помощью чисел весь мир, происходящие в нем события, раскрывающей прошлое и будущее, предсказывающей судьбы людей.

220

284

Для учеников Пифагора «4» было священным числом.
Символом дружбы у них были числа 220 и 284.
Числа 6 и 28 считались совершенными, они и были паролем пифагорейцев.
Другим паролем была пентаграмма – правильная пятиконечная звезда – опознавательный знак и символ здоровья для пифагорейцев

Пентаграмма Звёздчатый пятиугольник, образованный диагоналями правильного пятиугольника, содержит все известные пифагорейцам пропорции: арифметическую, геометрическую, гармоническую и так называемую золотую.

Таблица Пифагора Впервые таблица Пифагора – примерно в таком виде, в каком мы находим её на обложках тетрадей, появилась в сочинении Никомаха ( I — II вв.).

Теорема Пифагора:

В прямоугольном треугольнике квадраты, построенные на катетах, в сумме равновелики квадрату, построенному на гипотенузе

Однако в современной истории математики считается, что именно Пифагор дал его первое логически стройное доказательство. Со времен Пифагора появились сотни доказательств теоремы, она даже попала в Книгу рекордов Гиннеса

одна из главных теорем геометрии.

Представить себе эту теорему отдельно от имени великого грека уже невозможно, но на самом деле соотношение, которое она утверждает, было известно древним математикам

за много веков до Пифагора.

Пифагоровы деревья

Фигуры, которые

получаются при

бесконечном повторении

во всё меньшем

масштабе знаменитых

«пифагоровых штанов»,

знакомых всем по

доказательству теоремы

Пифагора.

Каждое из пифагоровых

деревьев обладает

замечательным

свойством самоподобия:

любой фрагмент дерева

при надлежащем увеличении

(и повороте) совпадает со

всем деревом

Пифагорейцы изучали варианты, в которых величины всех сторон прямоугольного треугольника выражаются целыми числами. Верёвочным треугольником со сторонами 3, 4 и 5 единиц пользовались ещё в Древнем Египте для построения прямых углов на местности

Египетский треугольник

Пифагоровы тройки-

Целые положительные числа, которые удовлетворяют соотношению

a 2 + b 2 = c 2

Их можно найти по формулам:

b = (a 2 -1):2 c = (a 2 +1):2

112

113

144

180

145

181

Симметричные тела

Для того, чтобы быть совершенно симметричным, геометрическое тело должно иметь равное число граней, встречающихся в углах, и эти грани должны быть правильными многоугольниками, то есть фигурами с равными сторонами и углами.
Пифагор, вероятно, был первым, кто сделал величайшее открытие, что есть только пять таких тел.

Правильные тела

К пяти симметричным правильным телам древних добавлена сфера — наиболее совершенная из всех сотворенных форм.

Гомер

Целые дни юный Пифагор проводил

у ног старца Гермодаманта,

слушая мелодии кифары, песни

Гомера.

Страсть к музыке и поэзии великого

Гомера Пифагор сохранил на всю

жизнь .

И, будучи великим мудрецом, окруженным толпой учеников, Пифагор начинал день с пения песен Гомера. «Гимн пифагорейцев восходящему солнцу»

К математическим наукам пифагорейцы относили арифметику, геометрию, астрономию и … музыку. Они установили, что высота звучания струны зависит от её длины, то есть опять же от числа!

В музыке Пифагор нашёл прямое доказательство своему знаменитому тезису: «Всё есть число»
Пифагорейцы создали первую математическую теорию музыки.

Слова «мелодия», «ритм» родились в Элладе, название слова«гамма» происходит от греческой буквы (гамма). Пифагор выстроил звукоряд. Шло время, и в звукоряде Пифагора обнаружились неожиданные изъяны. Музыкант – ученый Веркхмейстер повысив одни звуки, понизив другие, получил темперированный строй. Иоганн Себастьян Бах первым продемонстрировал достоинства строя. Бах сочинил величественный цикл прелюдий и фуги.

Пифагора по праву считают творцом акустики и основоположником теории музыки.

Арифметика – учение о количестве,

выражаемое числом;

музыка – учение, которое рассматривает

числа по отношению в звуке;

благодаря счастливому союзу,

музыка получила прочный

математический фундамент

гамм и универсальный язык нот.

Пифагор со своими учениками

ПИФАГОРЕЙСКАЯ АСТРОНОМИЯ Согласно Пифагору, положение каждого тела во вселенной определяется его достоинствами.

Бытовавшая в его дни концепция говорит о том, что Земля занимает центральное положение в солнечной системе, что планеты, включая Солнце и Луну, движутся вокруг Земли, что Земля плоская и квадратная.
В противоположность этому, не обращая внимания на критику, Пифагор говорил, что огонь является наиважнейшим из всех элементов, что центр является наиболее важной частью каждого тела и что точно так же, как огонь Весты находится в середине дома, так и середина Вселенной представляет пылающую сферу небесного сияния.

Символические афоризмы Пифагора

Среди них:

Помогай человеку в поднятии тяжести, но не помогай в сложении её.
Корми петуха, но не приноси его в жертву, поскольку посвящен он Солнцу и Луне.
Не позволяй ласточкам селиться в своём доме.
Не протягивай охотно свою правую руку.

“ Золотые стихи”,

Эти стихи открываются советом читателю возлюбить Бога, чтить великих героев и уважать духов природы. Затем человек призывается тщательно размышлять всю свою дневную жизнь и предпочитать сокровища ума и души земным накоплениям. Стихи также обещают человеку, что если он поднимет свою низшую материальную природу и будет культивировать самоконтроль, он будет замечен богами и соединится с ними, разделив с ними бессмертие.

Выводы

Пифагору — повезло больше, чем другим учёным древности. О нём сохранились десятки легенд и мифов, правдивых и выдуманных, реальных и вымышленных.Пифагор не только самый популярный учёный за всю историю человечества, но и самая загадочная личность, человек – символ и человек – фантом, философ и пророк. Основоположник дедуктивного научного знания – математики и родоначальник многих мистических знаний, учредитель религиозно – эпического братства и создатель научно – философской школы, ставшей воистину союзом Истины, Добра и Красоты.

При подготовке презентации были использованы…

Материалы публикаций в сети Internet .
Статьи из энциклопедий в школьной библиотеке.
Материалы электронных энциклопедий из школьной медиаколлекции.
М. «Первое сентября» 24-2001

Сокровище геометрии

Наталья Карпушина
«Наука и жизнь» №9, 2016

Римский архитектор Витрувий особо выделял теорему Пифагора «из многочисленных открытий, оказавших услуги развитию человеческой жизни», и призывал относиться к ней с величайшим почтением. Было это ещё в I веке до н. э. На рубеже XVI–XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.

Пифагоровы штаны

Теорема Пифагора едва ли не самая узнаваемая и, несомненно, самая знаменитая в истории математики. В геометрии она применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами a < b < c, усмотреть соотношение a² + b² = c² невозможно. Однажды известный американский логик и популяризатор науки Рэймонд Смаллиан, желая подвести учеников к открытию теоремы Пифагора, начертил на доске прямоугольный треугольник и по квадрату на каждой его стороне и сказал: «Представьте, что эти квадраты сделаны из кованого золота и вам предлагают взять себе либо один большой квадрат, либо два маленьких. Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, — и утверждение теоремы станет явным (рис. 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.

Фигуры, изображённые на рис. 1 и 2, напоминают простейший орнамент из квадратов и их равных частей — геометрический рисунок, известный с незапамятных времён. Им можно сплошь покрыть плоскость. Математик назвал бы такое покрытие плоскости многоугольниками паркетом, или замощением^*. При чём тут Пифагор? Оказывается, он первым решил задачу о правильных паркетах, с которой началось изучение замощений различных поверхностей. Так вот, Пифагор показал, что плоскость вокруг точки могут покрыть без пробелов равные правильные многоугольники только трёх видов: шесть треугольников, четыре квадрата и три шестиугольника.

4000 лет спустя

История теоремы Пифагора уходит в глубокую древность. Упоминания о ней содержатся ещё в вавилонских клинописных текстах времён царя Хаммурапи (XVIII век до н. э.), то есть за 1200 лет до рождения Пифагора. Теорема применялась как готовое правило во многих задачах, самая простая из которых — нахождение диагонали квадрата по его стороне. Не исключено, что соотношение a² + b² = c² для произвольного прямоугольного треугольника вавилоняне получили, попросту «обобщив» равенство a² + a² = c². Но им это простительно — для практической геометрии древних, сводившейся к измерениям и вычислениям, строгих обоснований не требовалось.

Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия. И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!

Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет. Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV–III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47». Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.

Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.

Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его… самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!

Первый математик

Пифагора Самосского (570–495 годы до н. э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII–VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.

Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции. С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.

Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно. Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов. Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.

Такое простое доказательство

Неизвестно, Пифагор сам обнаружил соотношение между длинами сторон в прямоугольном треугольнике или позаимствовал это знание. Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Оно, конечно, не сохранилось. По одной из версий, Пифагор мог воспользоваться разработанным в его школе учением о пропорциях. На нём основывалась, в частности, теория подобия, на которую опираются рассуждения. Проведём в прямоугольном треугольнике с катетами a и b высоту к гипотенузе c. Получим три подобных треугольника, включая исходный. Их соответствующие стороны пропорциональны, a : с = m : a и b : c = n : b, откуда a² = c · m и b² = c · n. Тогда a² + b² = c · (m + n) = c² (рис. 4).

Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, совсем простое: занимает всего-то несколько строк, не нужно ничего достраивать, перекраивать, вычислять… Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.

Такое доказательство не противоречило представлениям пифагорейцев о соизмеримости: изначально они считали, что отношение длин любых двух отрезков, а значит, и площадей прямолинейных фигур, можно выразить с помощью натуральных чисел. Никакие другие числа они не рассматривали, не допускали даже дробей, заменив их отношениями 1 : 2, 2 : 3 и т. д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости диагонали квадрата и его стороны. Все попытки численно представить длину этой диагонали — у единичного квадрата она равна √2 — ни к чему не привели. Проще оказалось доказать, что задача неразрешима. На такой случай у математиков есть проверенный метод — доказательство от противного. Кстати, и его приписывают Пифагору.

Существование отношения, не выражаемого натуральными числами, положило конец многим представлениям пифагорейцев. Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.

^* Паркет, или замощение, — разбиение плоскости многоугольниками (или пространства многогранниками) без пробелов и перекрытий.

Слова из теоремы Пифагора. Словарь

Изучение слов с помощью карточек и другие виды деятельности

Прочая учебная деятельность

Практика Ответьте на несколько вопросов по каждому слову. Используйте это, чтобы подготовиться к следующему тесту! Vocabulary JamСоревнуйтесь с другими командами в режиме реального времени, чтобы увидеть, кто правильно ответит на большинство вопросов! Проверка орфографии Проверьте свою орфографическую хватку. Прочитайте определение, послушайте слово и попробуйте написать его!

Инструменты для обучения

Викторина Создавайте и назначайте тесты своим ученикам, чтобы проверить их словарный запас. Назначайте занятия Назначайте учебные задания, включая практику, Vocabulary Jams и Spelling Bees, своим ученикам, и следите за их прогрессом в режиме реального времени.

прямоугольный треугольник
треугольник с одним прямым углом
В математике теорема Пифагора или теорема Пифагора — это отношение в евклидовой геометрии между тремя сторонами прямоугольный треугольник (прямоугольный треугольник).
38″> система координат
система, использующая координаты для определения местоположения
Содержание
1 Другие формы
2 доказательства
2.1 Доказательство с использованием подобных треугольников
2.2 Доказательство Евклида
2.3 Доказательство перестановкой
2.4 Алгебраические доказательства
2.5 Доказательство с использованием дифференциалов
3 Конверсия
4 Следствия и использование теоремы
4.1 Пифагоровы тройки
4.2 Несоизмеримые длины
4.3 Комплексные числа
4.4 Евклидово расстояние в различных системы координат
4.5 Тригонометрическое тождество Пифагора
4.6 Отношение к перекрестному произведению
5 Обобщения
5.1 Одинаковые фигуры с трех сторон
…
теорема
идея, принятая как доказуемая истина
В математике пифагорейцы теорема или теорема Пифагора — это отношение в евклидовой геометрии между тремя сторонами прямоугольного треугольника (прямоугольного треугольника).
гипотенуза
сторона прямоугольного треугольника, лежащая против прямого угла
Что касается областей, то в нем говорится:
В любом прямоугольном треугольнике площадь квадрата, сторона которого гипотенуза (сторона, противоположная прямому углу) равна сумме площадей квадратов, сторонами которых являются два катета (две стороны, пересекающиеся под прямым углом).
пифагорейский
или относящиеся к Пифагору или его геометрии
В математике Теорема Пифагора или теорема Пифагора — это отношение в евклидовой геометрии между тремя сторонами прямоугольного треугольника (прямоугольного треугольника).
объемный
относительно координат, определяющих положение в пространстве
Теорему можно обобщать различными способами, в том числе более высокоуровневыми. мерный пространств, к пространствам, не являющимся евклидовыми, к объектам, не являющимся прямоугольными треугольниками, и, действительно, к объектам, которые вовсе не треугольники, а n-мерные тела.
алгебраический
алгебры или относящейся к ней
Они очень разнообразны, включая как геометрические доказательства, так и алгебраических доказательств, некоторым из которых тысячи лет.
геометрия
математика точек и линий, кривых и поверхностей
В математике теорема Пифагора или теорема Пифагора является отношением в Евклидовом геометрия среди трех сторон прямоугольного треугольника (прямоугольного треугольника).
прямой угол
угол 90 градусов между двумя перпендикулярными линиями
Что касается площадей, то в нем говорится:
В любом прямоугольном треугольнике площадь квадрата, стороной которого является гипотенуза (сторона, противоположная прямой угол ) равен сумме площадей квадратов, сторонами которых являются две стороны (две стороны, которые пересекаются под прямым углом).
Пифагор
греческий философ и математик, доказавший теорему Пифагора; считается первым настоящим математиком (около 580-500 до н.э.)
В математике теорема Пифагора или Теорема Пифагора ‘ — это отношение в евклидовой геометрии между тремя сторонами прямоугольного треугольника (прямоугольного треугольника).
уравнение
математическое утверждение, что два выражения одинаковы
Теорему можно записать в виде уравнение , связывающее длины сторон a, b и c, часто называемое уравнением Пифагора:[1]
где c представляет длину гипотенузы, а a и b представляют длины двух других сторон.
угол
пространство между двумя пересекающимися линиями или плоскостями
В математике теорема Пифагора или теорема Пифагора — это соотношение в евклидовой геометрии между тремя сторонами прямоугольного треугольника (прямоугольный треугольник). угловой треугольник).
формула
группа символов, составляющих математическое выражение
Есть свидетельства того, что вавилонские математики понимали формула , хотя сохранилось мало свидетельств того, что они вписали ее в математическую структуру.

Создано 20 октября 2011 г.

11 лучших вкладов Пифагора

Сцена из «Афинской школы» Рафаэля показывает Пифагора в образе бородатого человека, утончающегося на макушке и пишущего пером. Он одет в тунику с рукавами, раскинутую по его ногам, и склоняет голову, чтобы писать, балансируя книгой на левом бедре.

Перед ним длинноволосый ребенок протягивает ему доску для письма. За ребенком стоит еще одна фигура женщины с длинными волосами, одетая в белый саван. Ближневосточный философ Аверроэс заглядывает через левое плечо, в то время как другая бородатая фигура, предположительно Анаксагор, заглядывает через его правое плечо и пишет заметки в маленьком блокноте.

Досократический греческий логик Пифагор — один из самых известных людей в мире, однако он не записал ни одной из своих теорий, и то, что мы знаем о нем сегодня, получено из других современных или более поздних источников, таких как картина описано выше. Первоначально на Самосе Пифагор основал школу в Кротоне на юге Италии, в которой преподавали как религию, так и логическое мышление.

Вот список из 11 лучших вкладов Пифагора:

1. Метемпсихоз

Хотя подробности уроков Пифагора остаются неизвестными, можно получить общее представление из других источников, таких как Аристотель, который пишет о уроки пифагорейцев без прямой ссылки на Пифагора.

Одним из фундаментальных принципов Пифагора, по-видимому, был метемпсихоз, то есть вера в то, что все духи богоподобны и что после смерти дух переходит в другое тело. Считается, что он перевоплотился в ученого Гермотима, увидевшего щит Евфорба в святилище Аполлона. Его последним проявлением был Пирр, рыбак с Делоса.

2. Нумерология

Как указывал Аристотель, пифагорейцы использовали науку в областях мистерий и спиритуализма без функционального применения. Базовая единица, монада, говорила о месте рождения всех вещей, а число два, диада, относилось к материи. Число семь было священным, потому что это было число планет, число струн на лире, и потому что день рождения Аполлона отмечался седьмого дня каждого месяца.

По словам немецкого ученого Буркерта, Пифагор не занимался математикой в том виде, в каком мы ее понимаем сегодня. Беркерт утверждает, что пифагорейцы в основном занимались основами арифметики, что в конечном итоге привело к зарождению современной математики.

3. Публичный образ жизни

И Платон, и древний оратор Исократ предполагают, что Пифагор был сторонником нового образа жизни. Школа или организация, которую Пифагор основал в Кротоне, действовала во многом подобно монастырю, и ее члены делили свое имущество во многом таким же образом. Они также были преданы друг другу, исключая посторонних.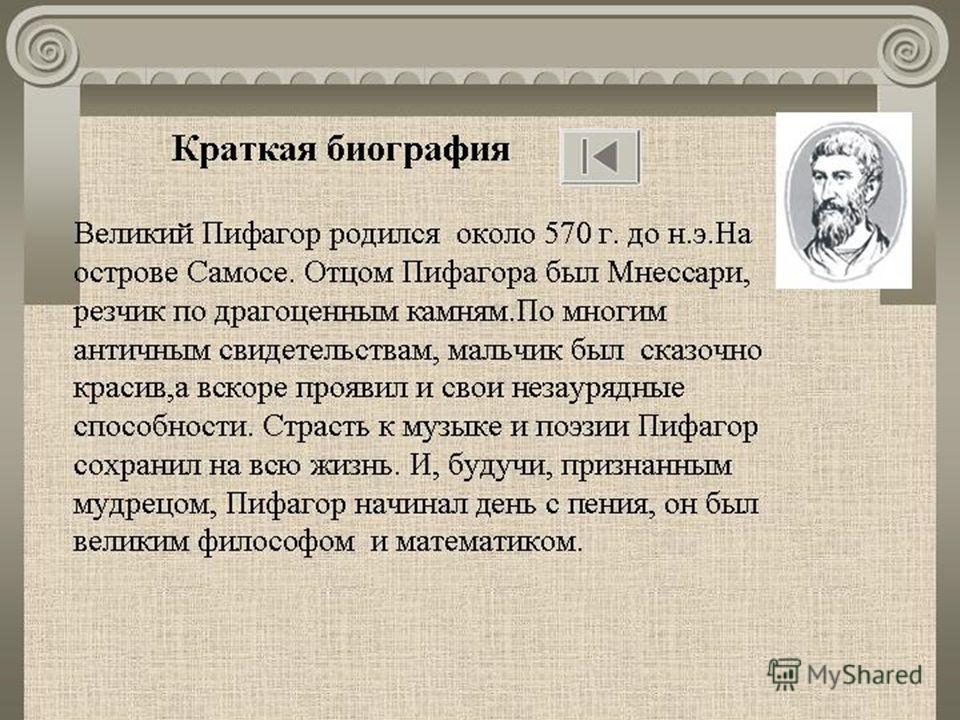 Одна из пифагорейских поговорок была koinà tà phílōn, что означало «У друзей все одинаково».

В пифагореизме было две группы: математики (студенты) и акусматики (слушатели). Акусматикои обычно считались «старыми мастерами» в чародействе, нумерологии и религиозных учениях, в то время как математики считались новаторской группой, которая была более прогрессивной, прагматичной и научной.

4. Музыка и образ жизни

Увлечение музыкой могло быть связано с любовью к Аполлону. Пифагорейцы считали, что музыка очищает дух и оказывает такое же действие, как и медицина на тело. В одном из рассказов Пифагора сообщается, что, когда он стал свидетелем того, как пьяные юноши пытались ворваться в дом женщины, он спел им, и «яростное упорство» молодых людей заставило замолчать.

Пифагор был первым, кто рекомендовал музыку в качестве рецепта. Он связал музыку с мастерством, дизайном, управлением, созданием семьи, общением и самосовершенствованием. Он думал, что можно привести души в соответствие с их совершенной природой, и с помощью музыки выполнял то, что называл «настройкой души».

Пифагор также связывал арифметику с музыкой и считал, что музыку нельзя рассматривать только как развлечение. Он считал, что музыка — это поток гармонии, божественное правило, направленное на устранение беспорядка и конфликтов в космосе. В соответствии с этим считалось, что музыка выполняет двойную функцию, поскольку, как и наука, она дает людям возможность заглянуть в структуры природы.

Пифагорейцы также придавали большое значение физическим упражнениям и рекомендовали ежедневные утренние прогулки и занятия спортом. Также были рекомендованы периоды самоанализа в начале и в конце каждого дня.

5. Космология

Пифагор был первым, кто предположил, что Земля представляет собой шар, но непонятно, что привело его к такому выводу. Возможно, это связано с его верой в то, что круги были самой прочной формой.

Его восприятие вселенной, скорее всего, было исключительно базовым: в то время земля все еще считалась фокусом вселенной, вокруг которой вращалось все. Пифагорейское представление о Вселенной было довольно прямолинейным и не принимало во внимание никаких наблюдений за движением планет.

Они верили, что все планеты движутся по гигантским кругам и что, когда они касаются друг друга, они издают звук. Они считали эти звуки мелодическими гармониями, и эта музыка стала известна как Музыка Сфер. Эту музыку не было слышно, потому что это был постоянный фоновый шум.

Пифагорейцы также верили, что земля, планеты и звезды вращаются вокруг центрального пламени, и день и ночь возникают из-за этого движения. Они верили, что по ту сторону пламени существует «противоземля». Поскольку они считали, что огонь важнее земли, средоточием вселенной должен быть огонь.

Пифагор первым понял, что Венера ночью и Венера в начале дня — одна и та же планета.

6. Математика

Пифагор положил начало идее системы счисления и, следовательно, началу математики. Для пифагорейцев подлинные числа были самым важным, а числа составляют мир.

7. Религиозные уроки

Религиозные уроки Пифагора основывались на принципе метемпсихоза, который гласит, что дух никогда не умирает и связан циклом перевоплощений до тех пор, пока не сможет освободиться от него посредством добродетели.

Считалось, что душа существует как в животной, так и в растительной жизни, хотя нет никаких доказательств того, что Пифагор думал, что дух может содержаться в растении. Однако он мог содержаться в теле существа, и Пифагор утверждал, что слышал голос мертвого товарища в завываниях избиваемой собаки.

8. Теорема Пифагора

Пифагор наиболее известен своими идеями в геометрии. Он был первым, кто предположил, что квадрат гипотенузы (сторона треугольника, противоположная прямому углу) эквивалентен сумме квадратов двух противоположных сторон.

Хотя эту гипотезу впервые выдвинули вавилоняне, Пифагор первым ее продемонстрировал. Также считается, что он изобрел тетрактис, треугольную фигуру, состоящую из 10 точек, расположенных в четыре ряда, по одной, двум, трем и четырем точкам в каждом ряду. Пифагор считал 10 идеальным числом.

9. Греческое рассуждение

Аристотель утверждает, что рассуждения Платона в значительной степени зависели от уроков пифагорейцев. Платон, возможно, также получил идею о том, что математические и динамические идеи стоят за логикой, наукой и моралью от Пифагора. Платон и Пифагор разделяли магический способ обращения с духом и его местом в материальном мире, и вполне вероятно, что на обоих повлиял орфизм, набор религиозных верований и практик, зародившихся в древнегреческом мире.

10. Раннее христианство

Историк Евсевий сравнивает Пифагора с Моисеем, в то время как Августин Гиппопотамский (354–430 гг. н.э.), раннехристианский богослов и философ, отверг теорию метемпсихоза Пифагора, фактически не называя его имени, но в целом выражал глубокое уважение для него. В «О Троице» Августин обсуждает скромность Пифагора, называя себя «почитателем проницательности», а не «мудрецом».

Примерно в то же время неопифагорейство начало становиться все более заметным, а неопифагорейский логик первого века Модерат из Гадеса сыграл важную роль в развитии пифагорейской философии чисел и классификации духа как «своего рода числовой гармонии».