Апория. Апории Зенона. Философия
Наверное, каждый сталкивался с таким словом, как «апория». Это и немудрено, ведь многие изучали в университете курс философии. Однако далеко не каждый знает сущность этого слова и сможет правильно его растолковать.
Апории Зенона Элейского – выдающийся памятник человеческой мысли. Это одна из интереснейших проблем в философии Древней Греции, которая показывает, насколько парадоксальными могут оказаться совершенно очевидные на первый взгляд вещи.
Зенон: краткая биография мудреца
О страницах жизни древнегреческого философа нам почти ничего неизвестно. Да и та информация, что до нас дошла, является весьма противоречивой.
Зенон Элейский – философ Древней Греции, родившийся в 490 году до нашей эры в Элее. Прожил 60 лет и умер (предположительно) в 430 году до нашей эры. Зенон был учеником и приемным сыном другого известного философа – Парменида. Кстати, если верить Диогену, то он был еще и любовником своего учителя, однако эти сведения решительно отвергнул грамматик Афиней.
Первый диалектик (по высказыванию Аристотеля) стал известен благодаря своим логическим умозаключениям, которые получили название «апории Зенона». Философия Зенона Элейского – вся состоит из парадоксов и противоречий, отчего становится еще интересней.
Трагическая смерть философа
Тайнами и загадками окутана жизнь и смерть великого философа. Он известен также как деятель политики, из-за которой и погиб. Зенон, как утверждают некоторые источники, возглавил борьбу против элейского тирана Неарха. Однако философ был арестован, после чего его многократно и изощренно пытали. Но даже под страшнейшими пытками философ не выдал своих боевых товарищей.
Существует две версии смерти Зенона Элейского. По одной из них его изощренно казнили – бросили в огромную ступу и истолкли насмерть. Согласно другой версии, во время разговора с Неархом, Зенон бросился на тирана и откусил его ухо, за что моментально был убит слугами.
Апории Зенона
Известно, что философ создал не менее сорока различных апорий, однако до нас дошли только девять из них. Среди самых популярных апорий Зенона «Стрела», «Ахиллес и черепаха», «Дихотомия» и «Стадий».
Среди самых популярных апорий Зенона «Стрела», «Ахиллес и черепаха», «Дихотомия» и «Стадий».
Древнегреческий философ, апориями которого до сих пор озадачен не один десяток современных исследователей, поставил под сомнение существование таких незыблемых категорий, как движение, множество и даже пространство! Дискуссии, спровоцированные парадоксальными высказываниями Зенона Элейского, ведутся до сих пор. Богомолов, Сватковский, Панченко и Манеев – вот далеко не полный список ученых, которые занимались этой проблемой.
Апория – это…
Так какова же суть этого понятия? И в чем состоит парадоксальность апорий Зенона Элейского?
Если перевести греческое слово «aporia», то апория – это «безвыходное положение» (дословно). Она возникает из-за того, что в самом предмете (или в его трактовке) спрятано определенное противоречие.
Можно говорить о том, что апория – это (в философии) проблема, решение которой сопряжено с большими трудностями.
Своими умозаключениями Зенон существенно обогатил диалектику. И хоть современные математики уверены, что они опровергли апории Зенона, они все равно таят в себе еще множество загадок.
И хоть современные математики уверены, что они опровергли апории Зенона, они все равно таят в себе еще множество загадок.
Если же трактовать философию Зенона, апория – это, в первую очередь, абсурдность и невозможность существования движения. Хотя сам философ, вероятнее всего, не употреблял этот термин вообще.
«Ахиллес и черепаха»
Рассмотрим более детально четыре самые известные апории Зенона Элейского. Первые две ставят под удар существование такого понятия, как движение. Это апория «Дихотомия» и апория «Ахиллес и черепаха».
Апория «Дихотомия» на первый взгляд кажется абсурдной и совершенно бессмысленной. Она утверждает, что любое движение не может закончиться. Более того, оно не может даже начаться. Согласно этой апории, чтобы пройти все расстояние, нужно вначале пройти его половину. А чтобы преодолеть его половину, нужно пройти половину половины этого расстояния и так до бесконечности. Таким образом, невозможно пройти бесконечное число отрезков за конечный (ограниченный) промежуток времени.
Более известной является апория «Ахиллес и черепаха», в которой философ решительно утверждает, что быстрый герой никогда не сможет догнать черепаху. Всё дело в том, что пока Ахиллес будет пробегать участок, отделяющий его от черепахи, та, в свою очередь, тоже проползет некоторое расстояние от него. Далее пока Ахиллес будет преодолевать это новое расстояние, черепаха сможет отползти еще на небольшое расстояние дальше. И так будет происходить до бесконечности.
«Стрела» и «Стадий»
Если первые две апории ставят под сомнение существование движения как такового, то апории «Стрела» и «Стадий» опротестовали дискретное представление времени и пространства.
В своей апории «Стрела» Зенон утверждает, что любая выпущенная из лука стрела неподвижна, то есть находится в состоянии покоя. Чем аргументирует философ это свое нелепое, казалось бы, утверждение? Зенон говорит, что летящая стрела неподвижна, ибо в каждый отдельно взятый момент времени она занимает в пространстве место, равное себе же. Так как это обстоятельство справедливо для абсолютно любого момента времени, то значит, что это обстоятельство справедливо и в целом. Таким образом, утверждает Зенон, любая летящая стрела находится в состоянии покоя.
Так как это обстоятельство справедливо для абсолютно любого момента времени, то значит, что это обстоятельство справедливо и в целом. Таким образом, утверждает Зенон, любая летящая стрела находится в состоянии покоя.
Наконец, в четвертой своей апории неординарный философ сумел доказать, что признание существования движения равняется, по сути, признанию того, что единица равняется своей половине!
Зенон Элейский предлагает вообразить три одинаковых ряда всадников на лошадях, выстроенных в шеренги. Предположим, что две из них двинулись в разные стороны, причем с одинаковой скоростью. Вскоре последние всадники этих шеренг окажутся на одной линии с серединой шеренги, которая осталась стоять на своем месте. Таким образом, каждая шеренга пройдет мимо половины шеренги, которая стоит, и мимо всего ряда, который двигается. И Зенон говорит, что один и тот же всадник за один промежуток времени пройдет одновременно и весь путь, и его половину. Другими словами, целая единица равняется своей же половине.
Вот мы и разобрались с этой непростой, но весьма увлекательной философской проблемой. Таким образом, апория – это, в философии, противоречие, которое таится в самом предмете либо в понятии о нем.
Прикладная философия: апории Зенона или не бойтесь ходячих мертвецов
Огурец горек. Брось его. «Наедине с собой. Размышления» Книга пятая. Строка 50.
Марк Аврелий, римский император из династии Антонинов, философ, представитель позднего стоицизма, последователь Эпиктета, последний из пяти хороших императоров
Забавно, весьма забавно, но применить в программировании — затруднительно, весьма затруднительно.
Комментарий к эссе «Прикладная философия: коронавирус встречает теорему Томаса». Александр, человек, чьё отношение к затруднениям неизвестно
Зачем человечеству философы и стоит ли их кормить? Вольный философ Мстислав Орлов вновь задумывается над вопросами, которые ему никто не задавал. С его точки зрения, границы применимости того или иного объекта зависят лишь от субъекта. “Вот дерево. Для чего оно, пока никак не используется? Практично ли оно, пока вам не нужна скамейка?”
С его точки зрения, границы применимости того или иного объекта зависят лишь от субъекта. “Вот дерево. Для чего оно, пока никак не используется? Практично ли оно, пока вам не нужна скамейка?”
Я мог бы навскидку перечислить вам сорок афоризмов, которыми Марк Аврелий вошёл в историю, и это не отменит того, что его слова, вырванные из контекста, теряют смысл и становятся несколько смешны. Поэтому призываю всех читать первоисточники, пользуясь переизбытком времени. Та же книга Диогена Лаэртского заставит вас хохотать и думать; при этом вы получите представления об античной философии, не искаженные всякими вольными философами. Каждому отличившемуся мыслителю Диоген посвятил отдельную главу. Если не знаете, с кого начать, то герой этого эссе — настолько интересная личность, что даже невозможно, верно,предположить, чем бы Зенон Элейский, философ V века, зарабатывал бы сегодня.
Точно уж, не был бы регулятором дорожного движения. Оно, с точки зрения Зенона, немыслимо. Философия, как и любая наука, нуждается в доказательствах и древний грек, не сдвигаясь с места, привёл аргументы.
Если не слышали, то даже лучше. Люди же, знакомые с творчеством Зенона в том или ином виде, могут просто пропустить следующие три абзаца.
«Апория» переводится с древнегреческого как «тупик». Это самый изящный способ разрушить чужую теорию, а точнее, найти некий эмпирический факт, о который быстро и легко разобьётся вражеские логические верные рассуждения.
Ахиллес — в данном случае, метафора чертовски хорошего бегуна. Черепаха — традиционно медленный и упорный спортсмен.
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Теперь, когда мы знаем, что Зенон на досуге любил подолгу глядеть на бега людей и животных, мы можем представить философа на ипподроме. Стал бы ли он зарабатывать там — вопрос к Зенону, первое же утверждение данного эссе всё ещё сохраняет свою истинность.
Стал бы ли он зарабатывать там — вопрос к Зенону, первое же утверждение данного эссе всё ещё сохраняет свою истинность.
Обязан предупредить: апории Зенона схожи с теоремой Ферма. Внешне простые логические задачки содержат в себе парадоксы. Зенон рвал шаблоны до того, как придумали для этого название.
У апорий, безусловно, была цель. Зенон, расставляя мины на пути философов, оперирующих категориями иначе, чем Парменид, просто защищал учителя в войне досократиков. «Ахиллесом и черепахой» Зенон пытался опровергнуть наши представления о делимости пространства и движении. В своё время это ему неплохо удалось. А вы что думали? Древнегреческие философы не стеснялись громить друг друга во всех смыслах. Причём не только на словах.
«Движенья нет, сказал мудрец брадатый. Другой смолчал и стал пред ним ходить» — эти известные строки Пушкина — лишь отображение давнего философского спора на тему движения.
Загадки без отгадок оставим журналам с вырванными страницами, а сами же снимем мнимое противоречие, оставленное нам Зеноном. Если перевести апорию на язык математики, мы получим простую задачку на определение суммы ряда. Для тех, кто не силён в рядах и их суммах, скажем просто: Ахиллес догонит черепаху.
Если перевести апорию на язык математики, мы получим простую задачку на определение суммы ряда. Для тех, кто не силён в рядах и их суммах, скажем просто: Ахиллес догонит черепаху.
Как всё это можно применить в программировании? — вот вопрос, ради которого и писалось данное эссе(автор обыгрывает комментарий, полученный к его предыдущей статье, относясь к обратной связи явно с большим вниманием. – Ред.).
Чтобы разрешить противоречие, найденное Зеноном, оказалось мало походить и посмеяться над стариком, как это сделал Диоген. Ещё неплохо создать математический анализ, разработать дифференциальное и интегральное счисления — как это всё применить в программировании Зенон не знал. Он просто придумывал проблемы, приучая нас к тому ходу мысли, который и позволил современной математике развиться до прикладного значения, лежащему в основе большинства социальных взаимодействий нашей эпохи.
А навык находить сумму ряда может пригодиться при преобразовании сигнала в ряд Фурье. Как это применить в философии — затруднительно, весьма затруднительно. В любом случае, попытка следовать чьему-то ходу мысли есть невольная попытка мыслить, как некто другой. Если выбрать хороший образец для подражания — худо не будет, это точно.
Как это применить в философии — затруднительно, весьма затруднительно. В любом случае, попытка следовать чьему-то ходу мысли есть невольная попытка мыслить, как некто другой. Если выбрать хороший образец для подражания — худо не будет, это точно.
Автор: Мстислав Орлов, вольный философ из Израиля
____________________
Подписывайтесь на наш канал телеграм
Поделиться ссылкой:
Апории Зенона философия — Docsity
Пермский Национальный Исследовательский Политехнический Университет «Апории Зенона» Работу выполнила студентка 1-го курса ГМУ-19-2Б Васильева Изабелль Пермь, 2020 Введение 1. Философия элеатов 2. Модели движения в античной натурфилософии 2.1 Содержание апорий о движении 2.2. Ахиллес и черепаха 2.3 Дихотомия 2.4 Летящая стрела 2.5 Критика апорий Аристотелем 2.6 Обсуждение в Новое время 3. Другие апории Зенона 3.1 Стадион 3.2 Множественность 3.3 О месте 3.4 Медимн зерна 4. Историческое значение апорий Зенона 5.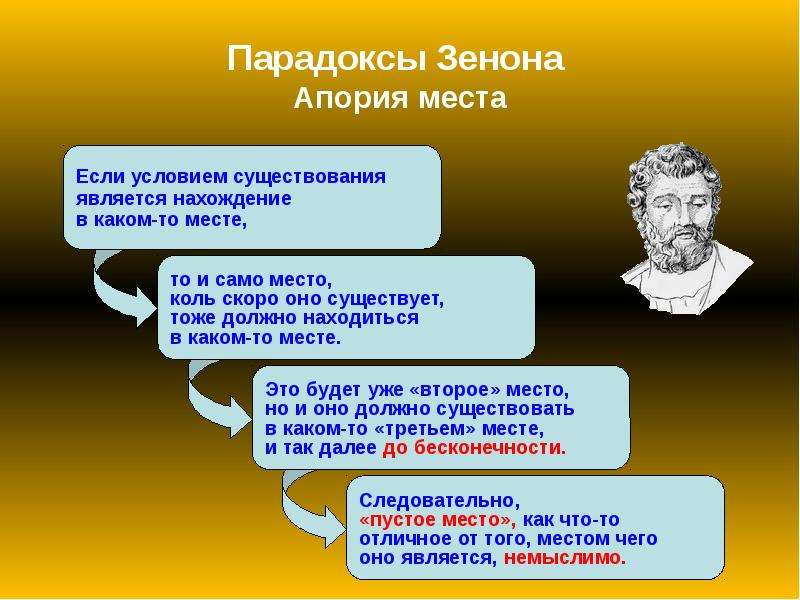 Литература 2. Модели движения в античной натурфилософии В V веке до н. э. древнегреческая математика достигла высокой ступени развития, и пифагорейская школа выражала уверенность, что математические закономерности лежат в основе всех законов природы. В частности, математическая модель движения в природе была создана на основе геометрии, которая к этому времени уже была достаточно глубоко разработана. Геометрия пифагорейцев опиралась на ряд идеализированных понятий: тело, поверхность, фигура, линия — и самым идеализированным было фундаментальное понятие точки пространства, не имеющей никаких собственных измеримых характеристик. Тем самым любая классическая кривая считалась одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие не вызывало проблем, но применение этого же подхода к реальному движению поставило вопрос, насколько правомерен такой внутренне противоречивый подход. Первым проблему ясно сформулировал Зенон Элейский в серии своих парадоксов (апорий).
Литература 2. Модели движения в античной натурфилософии В V веке до н. э. древнегреческая математика достигла высокой ступени развития, и пифагорейская школа выражала уверенность, что математические закономерности лежат в основе всех законов природы. В частности, математическая модель движения в природе была создана на основе геометрии, которая к этому времени уже была достаточно глубоко разработана. Геометрия пифагорейцев опиралась на ряд идеализированных понятий: тело, поверхность, фигура, линия — и самым идеализированным было фундаментальное понятие точки пространства, не имеющей никаких собственных измеримых характеристик. Тем самым любая классическая кривая считалась одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие не вызывало проблем, но применение этого же подхода к реальному движению поставило вопрос, насколько правомерен такой внутренне противоречивый подход. Первым проблему ясно сформулировал Зенон Элейский в серии своих парадоксов (апорий).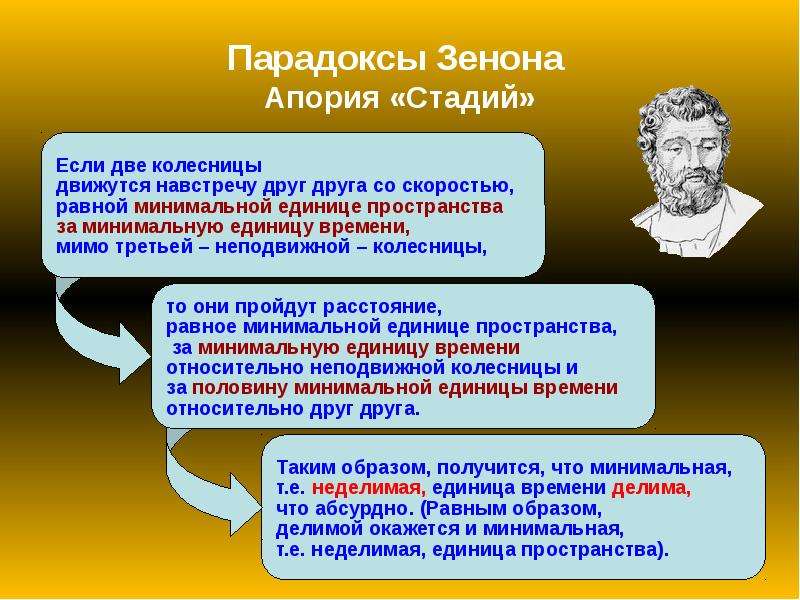 Апории и вообще взгляды Зенона нам известны только в кратком пересказе других античных философов, которые жили столетия спустя и хотя высоко ценили Зенона как «основателя диалектики», но чаще всего были его идейными противниками. Поэтому трудно достоверно выяснить, как формулировал апории сам Зенон, что он хотел показать или опровергнуть. По мнению большинства комментаторов, их цель — показать, что наше (математическое) представление о движении противоречиво. Эта точка зрения подтверждается тем, что элеатов в древности называли афизиками, то есть противниками науки о природе. В двух апориях «Ахиллес и Дихотомия» предполагается, что время и пространство непрерывны и неограниченно делимы; Зенон показывает, что это допущение приводит к логическим трудностям. Третья апория «Стрела», напротив, рассматривает время как дискретное, составленное из точек- моментов; в этом случае, как показал Зенон, возникают другие трудности. Отметим, что неправильно утверждать, будто Зенон считал движение несуществующим, потому что, согласно элейской философии, доказать не существование чего бы то ни было невозможно: «несуществующее немыслимо и невыразимо».
Апории и вообще взгляды Зенона нам известны только в кратком пересказе других античных философов, которые жили столетия спустя и хотя высоко ценили Зенона как «основателя диалектики», но чаще всего были его идейными противниками. Поэтому трудно достоверно выяснить, как формулировал апории сам Зенон, что он хотел показать или опровергнуть. По мнению большинства комментаторов, их цель — показать, что наше (математическое) представление о движении противоречиво. Эта точка зрения подтверждается тем, что элеатов в древности называли афизиками, то есть противниками науки о природе. В двух апориях «Ахиллес и Дихотомия» предполагается, что время и пространство непрерывны и неограниченно делимы; Зенон показывает, что это допущение приводит к логическим трудностям. Третья апория «Стрела», напротив, рассматривает время как дискретное, составленное из точек- моментов; в этом случае, как показал Зенон, возникают другие трудности. Отметим, что неправильно утверждать, будто Зенон считал движение несуществующим, потому что, согласно элейской философии, доказать не существование чего бы то ни было невозможно: «несуществующее немыслимо и невыразимо». Цель аргументации Зенона была более узкой: выявить противоречия в позиции оппонента. Часто в число апорий движения включают «Стадион», но по тематике этот парадокс скорее относятся к апориям бесконечности. Далее содержание апорий пересказывается с использованием современной терминологии. Под влиянием возникших философских споров сформировались два взгляда на строение материи и пространства: первый утверждал их бесконечную делимость, а второй — существование неделимых частиц, «атомов». Каждая из этих школ решала поставленные элеатами проблемы по-своему. 2.1 Содержание апорий о движении 2.2 Ахиллес и черепаха Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Цель аргументации Зенона была более узкой: выявить противоречия в позиции оппонента. Часто в число апорий движения включают «Стадион», но по тематике этот парадокс скорее относятся к апориям бесконечности. Далее содержание апорий пересказывается с использованием современной терминологии. Под влиянием возникших философских споров сформировались два взгляда на строение материи и пространства: первый утверждал их бесконечную делимость, а второй — существование неделимых частиц, «атомов». Каждая из этих школ решала поставленные элеатами проблемы по-своему. 2.1 Содержание апорий о движении 2.2 Ахиллес и черепаха Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.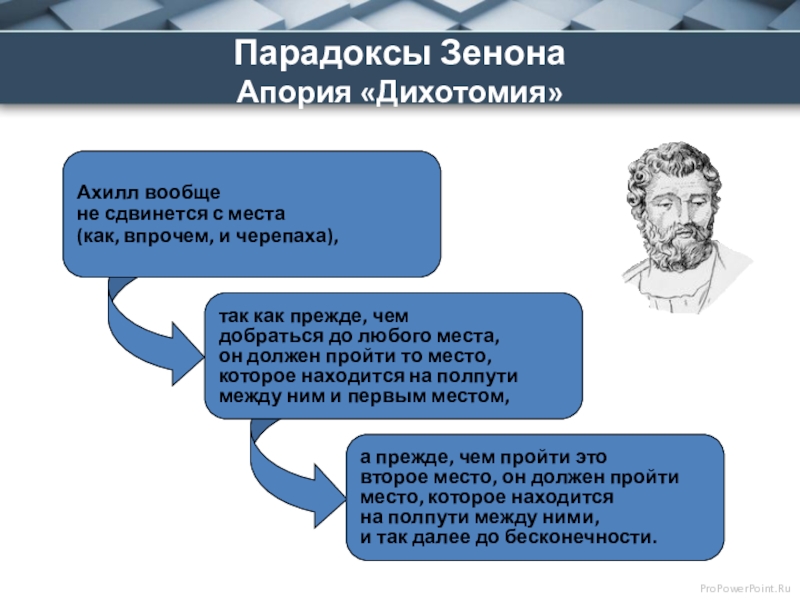 Диоген Лаэртский считал автором этой знаменитой апории Парменида, учителя Зенона. Черепаха как персонаж впервые упоминается у комментатора Симпликия; в тексте парадокса, приведённом у Аристотеля, быстроногий Ахиллес догоняет другого бегуна. 2.3 Дихотомия Чтобы преодолеть путь, нужно сначала преодолеть половину пути, а чтобы преодолеть половину пути, нужно сначала преодолеть половину половины, и так до бесконечности. Поэтому движение никогда не начнётся. Название «Дихотомия» (по-гречески: деление пополам) дано Аристотелем. 2.4 Летящая стрела Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда. 2.5 Критика апорий Аристотелем Бюст Аристотеля Аристотель (IV век до н. э.) считал материю непрерывной и неограниченно делимой. В книгах IV (главы 2, 3), VI (главы 2, 9) и VIII (глава 8) своей ) своей «Физики» он анализирует и отвергает рассуждения Зенона. В отношении апорий движения Аристотель подчёркивает, что хотя интервал времени можно неограниченно делить, но его нельзя составить из изолированных точек моментов и нельзя этой бесконечной делимости соотносить бесконечное время: «Зенон же рассуждает неправильно.
Диоген Лаэртский считал автором этой знаменитой апории Парменида, учителя Зенона. Черепаха как персонаж впервые упоминается у комментатора Симпликия; в тексте парадокса, приведённом у Аристотеля, быстроногий Ахиллес догоняет другого бегуна. 2.3 Дихотомия Чтобы преодолеть путь, нужно сначала преодолеть половину пути, а чтобы преодолеть половину пути, нужно сначала преодолеть половину половины, и так до бесконечности. Поэтому движение никогда не начнётся. Название «Дихотомия» (по-гречески: деление пополам) дано Аристотелем. 2.4 Летящая стрела Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда. 2.5 Критика апорий Аристотелем Бюст Аристотеля Аристотель (IV век до н. э.) считал материю непрерывной и неограниченно делимой. В книгах IV (главы 2, 3), VI (главы 2, 9) и VIII (глава 8) своей ) своей «Физики» он анализирует и отвергает рассуждения Зенона. В отношении апорий движения Аристотель подчёркивает, что хотя интервал времени можно неограниченно делить, но его нельзя составить из изолированных точек моментов и нельзя этой бесконечной делимости соотносить бесконечное время: «Зенон же рассуждает неправильно. Если всегда — говорит он — всякое тело покоится, когда оно находится в равном себе месте, а перемещающееся тело в момент теперь всегда находится в равном себе месте, то летящая стрела неподвижна. Но это неверно, потому что время не слагается из неделимых «теперь», а также никакая другая величина. Есть четыре рассуждения Зенона о движении, доставляющие большие затруднения тем, кто пытается их разрешить. Первое — о не существовании движения на том основании, что перемещающееся тело должно дойти до Эта апория аналогична парадоксу Галилея: бесконечное множество может быть равномощно своей части. 3.2 Множественность Часть апорий посвящена обсуждению вопроса о единстве и множественности мира. Если их существующих вещей много, то их должно быть столь много, сколько их есть — не больше и не меньше. А если их столь много, сколько их есть, то их число ограничено. Но если существующих вещей много, то их число неограничено: ибо всегда существуют другие вещи между существующими вещами, и снова другие между ними.
Если всегда — говорит он — всякое тело покоится, когда оно находится в равном себе месте, а перемещающееся тело в момент теперь всегда находится в равном себе месте, то летящая стрела неподвижна. Но это неверно, потому что время не слагается из неделимых «теперь», а также никакая другая величина. Есть четыре рассуждения Зенона о движении, доставляющие большие затруднения тем, кто пытается их разрешить. Первое — о не существовании движения на том основании, что перемещающееся тело должно дойти до Эта апория аналогична парадоксу Галилея: бесконечное множество может быть равномощно своей части. 3.2 Множественность Часть апорий посвящена обсуждению вопроса о единстве и множественности мира. Если их существующих вещей много, то их должно быть столь много, сколько их есть — не больше и не меньше. А если их столь много, сколько их есть, то их число ограничено. Но если существующих вещей много, то их число неограничено: ибо всегда существуют другие вещи между существующими вещами, и снова другие между ними. И так число существующих вещей неограничено. Сходные вопросы обсуждаются в диалоге Платона «Парменид», где Зенон и Парменид обстоятельно разъясняют свою позицию. На современном языке данное рассуждение Зенона означает, что множественное бытие не может быть актуально бесконечно и поэтому должно быть конечно, но к существующим вещам всегда можно добавить новые, что противоречит конечности. Вывод: бытие не может быть множественным. 3.3 О месте В изложении Аристотеля апория утверждает: если всё существующее помещается в известном пространстве (месте, греч. топос), то ясно, что будет и пространство пространства, и так идёт в бесконечность. Аристотель замечает на это, что место не есть вещь и не нуждается в собственном месте. Данная апория допускает расширенное толкование, поскольку элеаты не признавали пространство отдельно от тел, в нём расположенных, то есть отождествляли материю и пространство, ею занимаемое. Хотя Аристотель и отвергает рассуждение Зенона, но в своей «Физике» он приходит по существу к тому же выводу, что и элеаты: место существует лишь относительно тел, в нём находящихся.
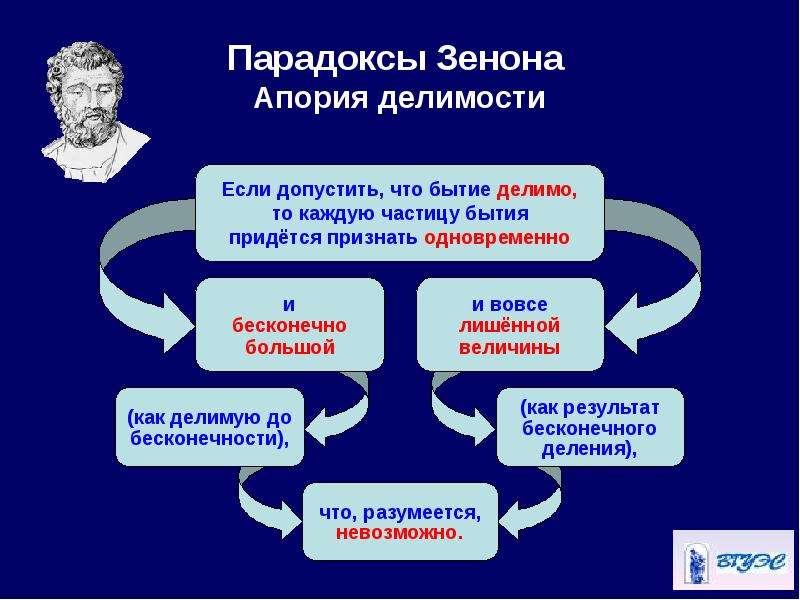
И так число существующих вещей неограничено. Сходные вопросы обсуждаются в диалоге Платона «Парменид», где Зенон и Парменид обстоятельно разъясняют свою позицию. На современном языке данное рассуждение Зенона означает, что множественное бытие не может быть актуально бесконечно и поэтому должно быть конечно, но к существующим вещам всегда можно добавить новые, что противоречит конечности. Вывод: бытие не может быть множественным. 3.3 О месте В изложении Аристотеля апория утверждает: если всё существующее помещается в известном пространстве (месте, греч. топос), то ясно, что будет и пространство пространства, и так идёт в бесконечность. Аристотель замечает на это, что место не есть вещь и не нуждается в собственном месте. Данная апория допускает расширенное толкование, поскольку элеаты не признавали пространство отдельно от тел, в нём расположенных, то есть отождествляли материю и пространство, ею занимаемое. Хотя Аристотель и отвергает рассуждение Зенона, но в своей «Физике» он приходит по существу к тому же выводу, что и элеаты: место существует лишь относительно тел, в нём находящихся. При этом Аристотель обходит молчанием естественный вопрос, как происходит изменение места при движении тела. 3.4 Медимн зерна Каждое отдельное зерно падает на землю бесшумно. Тогда отчего медимн (большой мешок) зерна падает с шумом? Формулировка Зенона подвергалась критике, так как парадокс легко объясняется ссылкой на порог восприятия звука — отдельное зерно падает не бесшумно, а очень тихо, поэтому звука падения не слышно. Смысл апории — доказать, что часть не подобна целому (качественно отличается от него) и, следовательно, бесконечная делимость невозможна. Аналогичные парадоксы предложил в IV веке до н. э. Евбулид — парадоксы «Лысый» и «Куча»: «одно зерно — не куча, добавление одного зерна не меняет дела, с какого же количества зёрен начинается куча?» 4. Историческое значение апорий Зенона Зенон вскрыл противоречия, в которые впадает мышление при попытке постигнуть бесконечное в понятиях. Его апории — это первые парадоксы, возникшие в связи с понятием бесконечного. Чёткое различение потенциальной и актуальной бесконечности у Аристотеля — во многом результат осмысления зеноновских апорий.
При этом Аристотель обходит молчанием естественный вопрос, как происходит изменение места при движении тела. 3.4 Медимн зерна Каждое отдельное зерно падает на землю бесшумно. Тогда отчего медимн (большой мешок) зерна падает с шумом? Формулировка Зенона подвергалась критике, так как парадокс легко объясняется ссылкой на порог восприятия звука — отдельное зерно падает не бесшумно, а очень тихо, поэтому звука падения не слышно. Смысл апории — доказать, что часть не подобна целому (качественно отличается от него) и, следовательно, бесконечная делимость невозможна. Аналогичные парадоксы предложил в IV веке до н. э. Евбулид — парадоксы «Лысый» и «Куча»: «одно зерно — не куча, добавление одного зерна не меняет дела, с какого же количества зёрен начинается куча?» 4. Историческое значение апорий Зенона Зенон вскрыл противоречия, в которые впадает мышление при попытке постигнуть бесконечное в понятиях. Его апории — это первые парадоксы, возникшие в связи с понятием бесконечного. Чёткое различение потенциальной и актуальной бесконечности у Аристотеля — во многом результат осмысления зеноновских апорий. Другие исторические заслуги элейских парадоксов: Рассуждения Зенона, изложенные точной и ясной прозой, являются первым в истории примером чисто логических доказательств. Именно этим определяется исключительно важное место Зенона в истории науки. Рассуждения по аналогии и поэтические фантазии, характерные для философов предыдущего поколения, сменились строгой дедуктивной логикой. Ясное указание на то, что наше представление о реальности (включая математическое) может быть неадекватно этой реальности; в последующем наука столкнулась с многочисленными примерами справедливости этого тезиса. Констатация того факта, что разделение непрерывности на отдельные точки (моменты), то есть смешение непрерывности и дискретности, есть противоречие. Как уже отмечалось выше, формирование античного атомизма было попыткой дать ответ на вопросы, поставленные апориями. В дальнейшем к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса, но сам факт непрерывного живого интереса к древней проблеме показывает её эвристическую плодотворность.
Другие исторические заслуги элейских парадоксов: Рассуждения Зенона, изложенные точной и ясной прозой, являются первым в истории примером чисто логических доказательств. Именно этим определяется исключительно важное место Зенона в истории науки. Рассуждения по аналогии и поэтические фантазии, характерные для философов предыдущего поколения, сменились строгой дедуктивной логикой. Ясное указание на то, что наше представление о реальности (включая математическое) может быть неадекватно этой реальности; в последующем наука столкнулась с многочисленными примерами справедливости этого тезиса. Констатация того факта, что разделение непрерывности на отдельные точки (моменты), то есть смешение непрерывности и дискретности, есть противоречие. Как уже отмечалось выше, формирование античного атомизма было попыткой дать ответ на вопросы, поставленные апориями. В дальнейшем к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса, но сам факт непрерывного живого интереса к древней проблеме показывает её эвристическую плодотворность. Различные точки соприкосновения апорий Зенона с современной наукой обсуждаются в статье Зураба Силагадзе. В заключении этой статьи автор приходит к выводу: Проблемы, поставленные два с половиной тысячелетия назад и с тех пор многократно изученные, до сих пор не исчерпаны. Парадоксы Зенона затрагивают фундаментальные аспекты реальности — локализацию, движение, пространство и время. Время от времени обнаруживаются новые и неожиданные грани этих понятий, и каждое столетие находит полезным снова и снова возвращаться к Зенону. Процесс достижения их окончательного разрешения представляется бесконечным, и наше понимание окружающего мира всё ещё неполно и фрагментарно. 5. Литература Античные философы о Зеноне — www.arhimed007.narod.ru/zenon.htm. Аристотель. Физика — www.lib.ru/POEEAST/ARISTOTEL/physic.txt. — В сборнике: Философы Греции. Основы основ: логика, физика, этика. — Харьков: ЭКСМО, 1999. — 1056 с. — ISBN 5-04-003348) своей -6 Платон. Парменид — www.philosophy.ru/library/plato/parmenid.
Различные точки соприкосновения апорий Зенона с современной наукой обсуждаются в статье Зураба Силагадзе. В заключении этой статьи автор приходит к выводу: Проблемы, поставленные два с половиной тысячелетия назад и с тех пор многократно изученные, до сих пор не исчерпаны. Парадоксы Зенона затрагивают фундаментальные аспекты реальности — локализацию, движение, пространство и время. Время от времени обнаруживаются новые и неожиданные грани этих понятий, и каждое столетие находит полезным снова и снова возвращаться к Зенону. Процесс достижения их окончательного разрешения представляется бесконечным, и наше понимание окружающего мира всё ещё неполно и фрагментарно. 5. Литература Античные философы о Зеноне — www.arhimed007.narod.ru/zenon.htm. Аристотель. Физика — www.lib.ru/POEEAST/ARISTOTEL/physic.txt. — В сборнике: Философы Греции. Основы основ: логика, физика, этика. — Харьков: ЭКСМО, 1999. — 1056 с. — ISBN 5-04-003348) своей -6 Платон. Парменид — www.philosophy.ru/library/plato/parmenid. html. — В сборнике: Платон, Сочинения в трёх томах. — М.: Мысль, 1968) своей —1972. — (Философское наследие). Лосев А. Ф. Зенон Элейский // Философская энциклопедия — nibiryukov.narod.ru/ nb_russian/nbr_teaching/nbr_teach_library/nbr_library_reference/ nbr_reference_losev_zenon_eleyskiy.htm. — М.: Советская энциклопедия, 1962 Зенон Элейский — www.krugosvet.ru/enc/gumanitarnye_nauki/filosofiya/ZENON_ELESKI.html. — Энциклопедия Кругосвет.
html. — В сборнике: Платон, Сочинения в трёх томах. — М.: Мысль, 1968) своей —1972. — (Философское наследие). Лосев А. Ф. Зенон Элейский // Философская энциклопедия — nibiryukov.narod.ru/ nb_russian/nbr_teaching/nbr_teach_library/nbr_library_reference/ nbr_reference_losev_zenon_eleyskiy.htm. — М.: Советская энциклопедия, 1962 Зенон Элейский — www.krugosvet.ru/enc/gumanitarnye_nauki/filosofiya/ZENON_ELESKI.html. — Энциклопедия Кругосвет.
Смысл и разрешение апории Зенона «Стрела»
Зенон Элейский, ученик Парменида, сформулировал множество апорий, в которых показывал противоречивость движения, пространства и множества. Один из парадоксов под названием «Стрела» звучит так:
Летящая стрела в каждый момент времени неподвижна, а раз так, то она неподвижна в любое время. Следовательно, она неподвижна всегда.
Этот парадокс наглядно показывает различие между чувственным восприятием и мышлением. И, соответственно, он показывает различие между вещью как предметом восприятия и вещью как предметом мышления.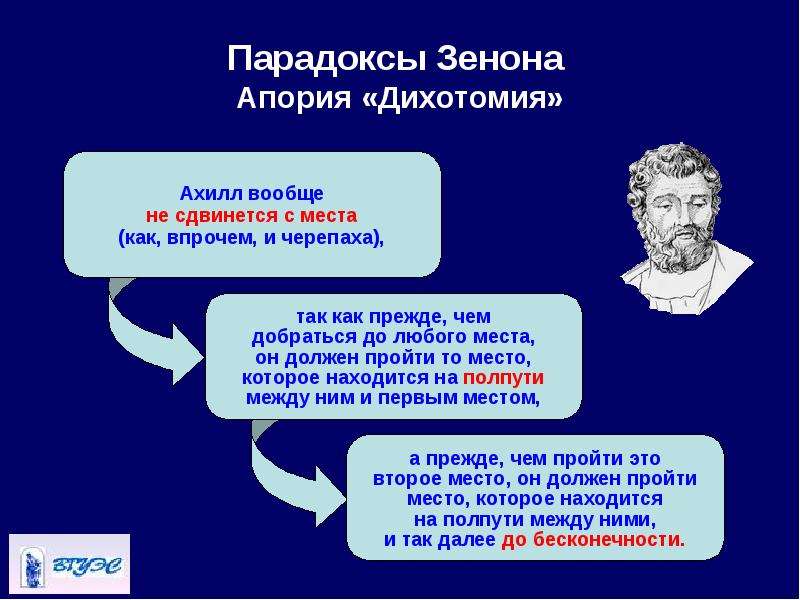
Для восприятия то, что стрела летит — это наглядно данный факт, но для мышления стрела является неподвижной. Почему?
Объяснение
Как мы знаем, любая вещь — это воплощенный в материи смысл. Вещь — это единство противоположностей — смысла (т.е. определённого бытия) и инобытия, или материи.
Замечу, что в философии материя — это не что-то определённое, а лишь отрицание смысла. Сам смысл, полаганием своей определённости задаёт свою противоположность, материю. Поэтому, материя — это не-смысл, не-бытие, или инобытие. Та материя, с которой имеют дело естественные науки — это уже так или иначе оформленная и осмысленная материя. В философии она обозначается понятием субстрат.
Итак, определённость смысла создаёт его отрицание — инобытие. Но сама эта противоположность двух создаёт и то третье, что их объединяет. Граница, разделяющая смысл и его инобытие, является и тем, в чём они совпадают. Такое совпадение смысла и его отрицания обозначается категорией становления.
Понятие становления — это наиболее общий термин, включающий в себя все родственные ему понятия — движение, изменение, развитие, и прочее.
Стало быть, любая вещь — это единство следующих моментов:
- Единство, или цельность. Вещь — это то целое, которое объединяет все свои моменты и проявления.
- Смысл (определённость). Вещь — это нечто логически определённое. Это то, что становится, субъект становления.
- Материя, которая воплощает на себе данный смысл. Это вообще та среда, в которой смысл становится, развёртывается.
- И, собственно, становление. Это сам процесс развёртывания, «размазывания» единого смысла в протяжённый континуум. Именно в сфере становления появляются пространство и время, которые превращают исходную точку сконцентрированного в себе смысла — в линии, плоскости, объёмы и их последовательное протекание.
Важно то, что смысл, воплощаясь в материи, т.е. попадая в сферу, где всё течёт и меняется, вместе с тем остаётся самотождественным, т.
Если речь идет о стреле, то стрела, которая летит, в каждый момент времени другая, но при этом, это та же самая стрела. Потому что меняться может только то, что в чем-то неизменно. И это неизменное — это ее смысл.
Отсюда ясно, что,
- поскольку стрела — это смысл, постольку она пребывает вне всякого становления. А значит — не движется.
- Поскольку она есть воплощенный в материи смысл, постольку она становится, т.е. движется и изменяется.
- Но поскольку стрела — это единство смысла и его инобытийного воплощения, постольку она и движется, и не движется. Изменяясь, она остаётся тождественной самой себе.
Поэтому, материальная стрела движется, но стрела как смысл — не движется. Более того, можно сказать, что движется не стрела, а вся инобытийная среда, в которой воплотился смысл стрелы, тогда как сам ее смысл остаётся неподвижным.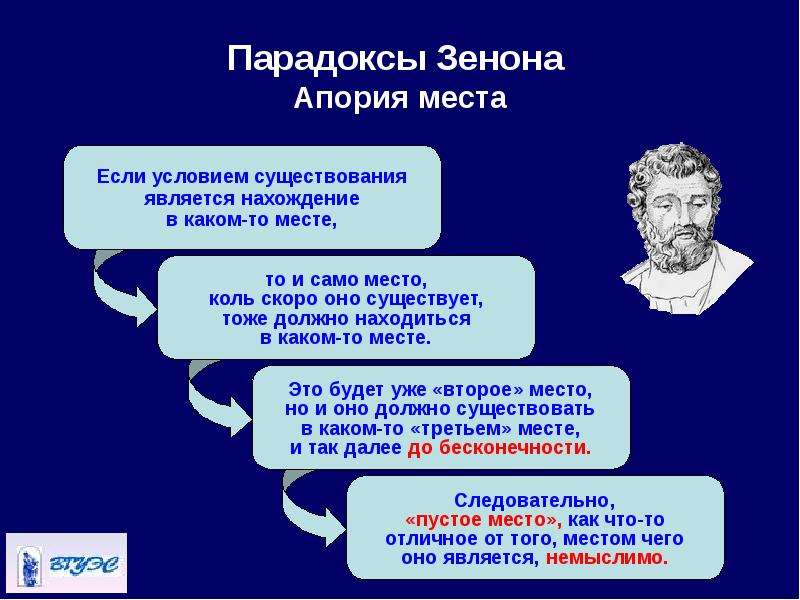
Дискретная вселенная
Некоторые, чтобы избежать парадокса, объявляют пространство и время прерывными. Дескать, в каждый квант времени стрела действительно покоится, просто каждый раз она занимает новое положение в пространстве.
Но тогда возникает вопрос: откуда мы знаем, что в каждый новый момент времени в каждой новой точке пространства присутствует та же самая стрела? Если она действительно та же самая, значит, при дискретности пространства и времени всё равно существует непрерывность смысла. Значит, и в этом случае мы должны признать единую смысловую сферу, охватывающую все моменты становления мира и гарантирующую его самотождественность.
Таким образом, в любом случае, мир как целое представляет собой единство прерывности и непрерывности, дискретности и континуальности.
Заключение
Как видим, в парадоксе Зенона ничего парадоксального нет, он просто описывает то, каким является мир с точки зрения целого — как единство противоположностей.
Это парадоксально только для рассудочного мышления, которое делит континуум становления на отдельные моменты, но «не дотягивает» до того, чтобы охватить эти моменты целиком и увидеть их единство.
В мире противоречиво вообще всё. Даже высказывание «стрела летит» содержит в себе противоречие: оно и указывает на неизменный субъект высказывания (стрела), и на изменение этого неизменного субъекта (летит). Таким образом, сказать «стрела летит» — это всё равно, что сказать «неизменное изменяется», что противоречиво. Но противоречия нужно не избегать, а учиться понимать их, чтобы подняться с уровня рассудка на уровень ума (или, по-гегелевски, разума). Именно в уме, в охватывающей противоположности сфере мысли, лежит и исток любого противоречия, и его разрешение.
Даже когда мы просто увидели стрелу и произнесли «стрела», мы этим актом обнаружили противоположности. Мы перешли от хаоса чувственных бесформенных впечатлений, к четкой оформленности и неподвижности смысла. То есть, перешли от становления к нестановящемуся, от времени к вневременному.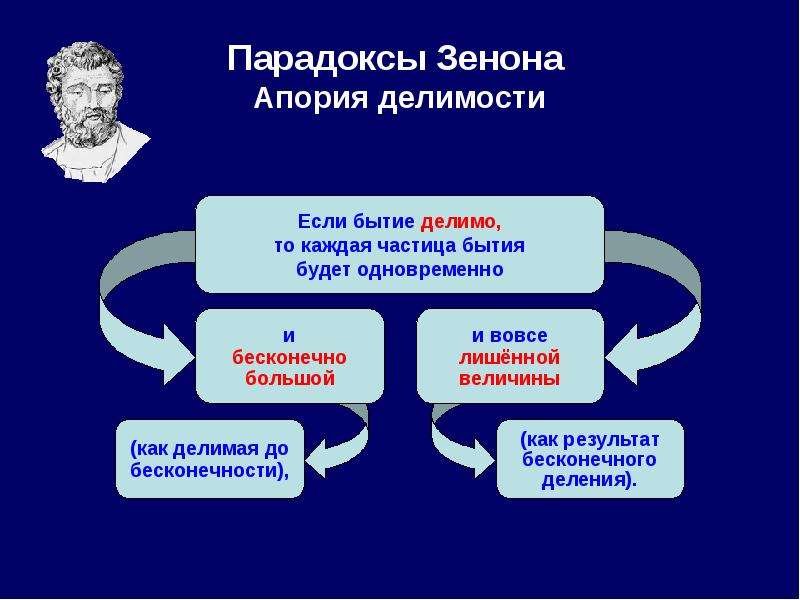
В каждом таком акте осмысления мы прикасаемся к вечности. И так, в потоке бессмысленного становления, мы начинаем видеть присутствие неизменного смысла.
Апории Зенона. Философия элеатов | Physics.Math.Code
«Вопрос о бесконечной делимости пространства (бесспорно, поставленный еще ранними пифагорейцами) привел, как известно, к значительным затруднениям в философии: от Элеатов до Больцано и Кантора математики и философы не в силах были разрешить парадокса — как конечная величина может состоять из бесконечного числа точек, не имеющих размера». Николя Бурбаки
Апории о движении
Ахиллес и черепаха
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползет сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползет еще десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Дихотомия
Чтобы преодолеть путь, нужно сначала преодолеть половину пути, а чтобы преодолеть половину пути, нужно сначала преодолеть половину половины, и так до бесконечности. Поэтому движение никогда не начнется.
Летящая стрела
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
Апории Зенона — внешне парадоксальные рассуждения на тему о движении и множестве, автором которых является древнегреческий философ Зенон Элейский (V век до н. э.). Современники упоминали более 40 апорий Зенона, до нас дошли 9, обсуждаемые в «Физике» и в других трудах Аристотеля, в комментариях Симпликия, Филопона и Фемистия к Аристотелю; одна апория из этих 9 приводится также у Диогена Лаэртского, апории о множестве обсуждаются в диалоге Платона «Парменид». Комментатор Элиас (Элий, VI век) сообщает, что Зенон высказал 40 рассуждений (эпихейрем) о множестве и пять — о движении:
Он составил для своего учителя Парменида, который утверждал, что сущее одно по виду, но множественно согласно очевидности, {аргументацию} из сорока эпихейрем в пользу того, что сущее одно, так как считал, что быть союзником учителя — это хорошо. Ещё как-то, защищая того же учителя, утверждавшего, что сущее неподвижно, он выдвинул пять эпихейрем в пользу того, что сущее неподвижно. Антисфен-киник, который не смог на них возразить, встал и стал ходить, полагая, что доказательство делом сильнее всякого возражения словом.
Ещё как-то, защищая того же учителя, утверждавшего, что сущее неподвижно, он выдвинул пять эпихейрем в пользу того, что сущее неподвижно. Антисфен-киник, который не смог на них возразить, встал и стал ходить, полагая, что доказательство делом сильнее всякого возражения словом.
Наиболее известны парадокс «Ахиллес и черепаха» и другие апории Зенона о движении, которые обсуждаются более двух тысячелетий, им посвящены сотни исследований. Платон в «Пармениде» их не упоминает, поэтому В. Я. Комарова предполагает, что парадоксы движения были написаны Зеноном позднее других.
Ошибочно воспринимать эти рассуждения как софизмы или полагать, что с появлением высшей математики все апории разрешены. Бертран Рассел писал, что апории Зенона «в той или иной форме затрагивают основания почти всех теорий пространства, времени и бесконечности, предлагавшихся с его времени до наших дней». «Проблематика аргументов Зенона далеко выходит за пределы конкретной исторической ситуации, обусловившей их появление. Анализу апорий Зенона посвящена колоссальная литература; особенно большое внимание им уделялось в последние сто лет, когда математики стали усматривать в них предвосхищение парадоксов современной теории множеств». Научные дискуссии, вызванные рассуждениями Зенона, существенно углубили понимание таких фундаментальных понятий, как роль непрерывного и дискретного (прерывного) в природе, адекватность физического движения и его математической модели и др. Эти дискуссии продолжаются и в настоящее время (см. список литературы), прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось.
Анализу апорий Зенона посвящена колоссальная литература; особенно большое внимание им уделялось в последние сто лет, когда математики стали усматривать в них предвосхищение парадоксов современной теории множеств». Научные дискуссии, вызванные рассуждениями Зенона, существенно углубили понимание таких фундаментальных понятий, как роль непрерывного и дискретного (прерывного) в природе, адекватность физического движения и его математической модели и др. Эти дискуссии продолжаются и в настоящее время (см. список литературы), прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось.
Философия элеатов
Элейская философская школа (элеаты) существовала в период с конца VI века до н. э. до первой половины V века до н. э., родоначальником её считается Парменид, учитель Зенона. Школа разработала своеобразное учение о бытии. Парменид изложил свои философские взгляды в поэме, от которой до нас дошли отдельные фрагменты.
Элеаты отстаивали единство бытия, считая, что представление о множественности вещей во Вселенной ошибочно. Бытие элеатов полно, реально и познаваемо, однако вместе с тем оно нераздельно, неизменно и вечно, у него нет ни прошлого, ни будущего, ни рождения, ни смерти. Мышление, говорилось в поэме Парменида, по своему содержанию тождественно предмету мышления («одно и то же — мышление и то, о чем мысль»). Далее Парменид логически выводит характеристики истинно сущего: оно «не возникло, не уничтожимо, целокупно [не имеет частей, единственно, неподвижно и нескончаемо во времени]».
Бытие элеатов полно, реально и познаваемо, однако вместе с тем оно нераздельно, неизменно и вечно, у него нет ни прошлого, ни будущего, ни рождения, ни смерти. Мышление, говорилось в поэме Парменида, по своему содержанию тождественно предмету мышления («одно и то же — мышление и то, о чем мысль»). Далее Парменид логически выводит характеристики истинно сущего: оно «не возникло, не уничтожимо, целокупно [не имеет частей, единственно, неподвижно и нескончаемо во времени]».
Познание этого целостного мира возможно только путем разумных (логических) рассуждений, а чувственная картина мира, включая наблюдаемые движения, обманчива и противоречива. С этих же позиций элеаты впервые в науке поставили вопрос о допустимости научных понятий, связанных с бесконечностью.
Как отмечают В. Ф. Асмус и ряд других историков, элеаты отрицали не возможность восприятия движения и множественности мира, а их мыслимость, то есть совместимость с логикой. Элеаты выявляли неизбежные, с их точки зрения, противоречия, возникающие при применении к природе научных понятий того времени, что подтверждало позицию Парменида, рационально-логический подход которого позволял этих противоречий избежать. Отстаивая свои взгляды в философских спорах, Зенон и другие элеаты использовали изощренную логическую аргументацию, и важной ее частью были апории Зенона, доказывающие нелогичность и противоречивость взглядов оппонентов.
Отстаивая свои взгляды в философских спорах, Зенон и другие элеаты использовали изощренную логическую аргументацию, и важной ее частью были апории Зенона, доказывающие нелогичность и противоречивость взглядов оппонентов.
***
Апории и вообще взгляды Зенона нам известны только в кратком пересказе других античных философов, которые жили столетия спустя и хотя высоко ценили Зенона как «основателя диалектики», но чаще всего были его идейными противниками. Поэтому трудно достоверно выяснить, как формулировал апории сам Зенон, что он хотел показать или опровергнуть. Согласно наиболее распространенной точке зрения, идущей от Платона, апории были направлены на защиту монизма философии Парменида от обыденных представлений о движении и множественности вещей; оппонентами Зенона могли быть сторонники здравого смысла. Некоторые учёные считают, что аргументы Зенона были связаны с размышлениями о ранних математических учениях пифагорейцев, поскольку апории фактически ставили под сомнение применение количественных подходов к физическим телам и пространственной протяженности. Эта точка зрения подтверждается тем, что элеатов в древности называли афизиками, то есть противниками науки о природе.
Эта точка зрения подтверждается тем, что элеатов в древности называли афизиками, то есть противниками науки о природе.
В V веке до н. э. древнегреческая математика достигла высокой ступени развития, и пифагорейская школа выражала уверенность, что математические закономерности лежат в основе всех законов природы. В частности, математическая модель движения в природе была создана на основе геометрии, которая к этому времени уже была достаточно глубоко разработана. Геометрия пифагорейцев опиралась на ряд идеализированных понятий: тело, поверхность, фигура, линия — и самым идеализированным было фундаментальное понятие точки пространства, не имеющей никаких собственных измеримых характеристик. Тем самым любая классическая кривая считалась одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие не вызывало проблем, но применение этой схемы к реальному движению поставило вопрос, насколько правомерен такой внутренне противоречивый подход. Первым проблему ясно сформулировал Зенон Элейский в серии своих парадоксов (апорий).
Первым проблему ясно сформулировал Зенон Элейский в серии своих парадоксов (апорий).
В двух апориях (Ахиллес и Дихотомия) предполагается, что время и пространство непрерывны и неограниченно делимы; Зенон показывает, что это допущение приводит к логическим трудностям. Третья апория («Стрела»), напротив, рассматривает время как дискретное, составленное из точек-моментов; в этом случае, как показал Зенон, возникают другие трудности. Отметим, что неправильно утверждать, будто Зенон считал движение несуществующим, потому что, согласно элейской философии, доказать несуществование чего бы то ни было невозможно: «несуществующее немыслимо и невыразимо». Цель аргументации Зенона была более узкой: выявить противоречия в позиции оппонента.
Под влиянием возникших философских споров сформировались два взгляда на строение материи и пространства: первый утверждал их бесконечную делимость, а второй — существование неделимых частиц, «атомов». Каждая из этих школ решала поставленные элеатами проблемы по-своему.
Полемика вокруг зеноновских апорий продолжилась и в Новое время. До XVII века интерес к апориям не отмечается, и их аристотелевская оценка являлась общепринятой. Первое серьезное исследование предпринял французский мыслитель Пьер Бейль, автор известного «Исторического и критического словаря» (1696). В статье о Зеноне Бейль подверг критике позицию Аристотеля и пришёл к выводу, что Зенон прав: понятия времени, протяжённости и движения связаны с трудностями, непреодолимыми для человеческого ума.
Сходные с апориями темы затронуты в антиномиях Канта. Гегель в своей «Истории философии» подчеркнул, что Зенонова диалектика материи «не опровергнута до сегодняшнего дня». Гегель оценил Зенона как «отца диалектики» не только в античном, но и в гегелевском смысле слова диалектика. Он отметил, что Зенон различает чувственно воспринимаемое и мыслимое движение. Последнее, в соответствии со своей философией, Гегель описал как сочетание и конфликт противоположностей, как диалектику понятий. Гегель не даёт ответа на вопрос, насколько этот анализ приложим к реальному движению, ограничившись выводом: «Зенон осознал определения, содержащиеся в наших представлениях о пространстве и времени, и обнаружил заключающиеся в них противоречия».
***
А. М. Анисов.«Апории Зенона и проблема движения»
Нашей целью будет не реконструкция зеноновских аргументов, а стремление понять с точки зрения современной науки, на какие реальные трудности в анализе движения указал Зенон Элейский. Именно указал, поскольку о попытке приписать непосредственно Зенону современную постановку проблем движения не может быть и речи. Кстати говоря, эта постановка в логико-философской литературе не отличается единством. Нередко ответственность за парадоксы движения возлагается на неточность и размытость используемых понятий. Уточним понятия – парадоксы исчезнут. Мы с этим не согласны. Апории Зенона касаются самих основ человеческого миропонимания. Они требуют не просто уточнения понятий, а выбора философской платформы объяснения реальности. Поскольку дело построения таких платформ не может быть завершено, пока существует мыслящий разум, на выборе одной из них лежит печать неизбежной исторической ограниченности. Сказанное, разумеется, в полной мере относится и к построениям в данной статье.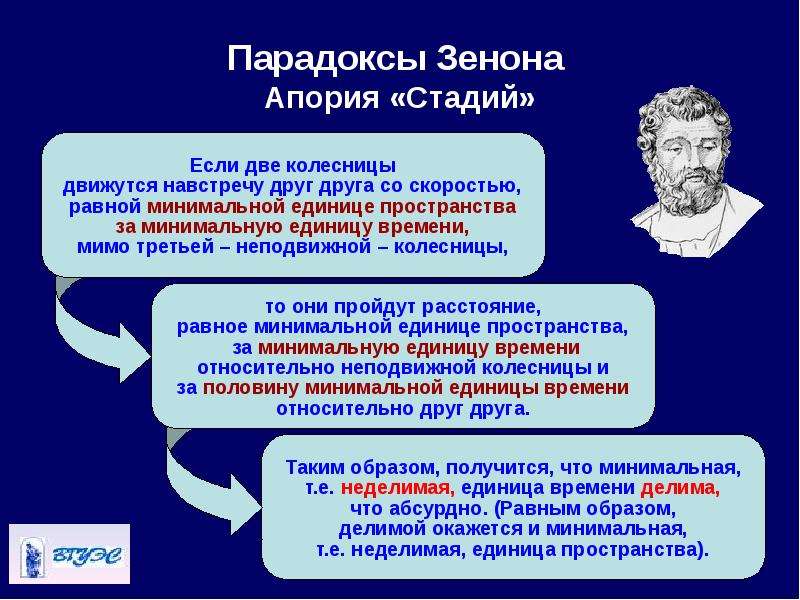 Но сегодня, несомненно, мы понимаем и знаем больше, чем два с половиной тысячелетия назад, а завтра, возможно, удастся продвинуться вперед еще дальше.
Но сегодня, несомненно, мы понимаем и знаем больше, чем два с половиной тысячелетия назад, а завтра, возможно, удастся продвинуться вперед еще дальше.
Cкачать книги и прослушать аудио-версию Элейской школы в нашей группе в VK
Еще много полезного и интересного вы сможете найти на наших ресурсах:
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Апории Зенона в свете современной логики
7. «Предикация»
Во-первых, Предикация – это формальное установление связей между субъектом и предикатом.
Одним из наиболее сомнительных
парадоксов Зенона является рассуждение
о предикации. В этом рассуждении
Зенон выдвигает идею о том, что
вещь не может быть единой и иметь
множество предикатов в одно и
то же время.
Платон растолковывает это рассуждение следующим образом: «Если вещи множественны, они должны быть и подобными, и неподобными (неподобными, поскольку они не являются одним и тем же, и подобными, поскольку общее у них то, что они не являются одним и тем же). Однако, это невозможно, поскольку неподобные вещи не могут быть подобными, а подобные неподобными. Следовательно, вещи не могут быть множественны». Этот парадокс был приписан Зенону из-за того, что в нем имеет место критика множественности и косвенный тип доказательства, характерный ему.
8.Современный взгляд на апории Зенона:
Довольно часто появлялись
и до сих пор появляются попытки
математически опровергнуть рассуждения
Зенона и тем самым «закрыть тему». Например,
построив ряд из уменьшающихся интервалов
для апории «Ахиллес и черепаха», можно
легко доказать, что он сходится, так что
Ахиллес обгонит черепаху. Но эти опровержения
подменяют суть спора. В апориях Зенона
речь идёт не о математической модели,
а о реальном движении. Зенон как раз и
ставит под сомнение применимость к реальному
движению идеализированных математических
понятий.
Зенон как раз и
ставит под сомнение применимость к реальному
движению идеализированных математических
понятий.
9. Заключение:
Заключение:
Изучив различные литературные источники, мною был сделан вывод, что апории Зенона вполне актуальны и в наши с вами дни. Они затрагивают действительно глубокие и сложные вопросы, ответы на которые порой бывают противоречивы. Полемика вокруг зеноновских апорий продолжилась и в Новое время. Апории Зенона стало популярно даже в таких сферах, как история, литература, искусство.
Они волнуют умы как
выдающихся математиков и философов, так
и людей решивших испытать свои силы в
этих областях, вплоть до наших с вами
дней.
В апориях «Дихотомия» и «Ахилл и черепаха»
нам повествуют о невозможности движения,
исходя из того, что пространство бесконечно
делится на точки, а время – на мгновения.
В «Летящей стреле» и «Стадие» нам доказывают,
что движение также невозможно в том случае,
когда мы делаем предположение, что время
и пространство делится не до бесконечности,
а до неделимых единиц, говоря другими
словами, время и пространство состоят
из атомов. 9
9
Четырьмя парадоксами Зенон очень хорошо достигает того, чего хотел. Он логически строго показывает, что в пифагорейских представлениях о движении, пространстве и времени что-то неверно.
«Трудности, нашедшие отражение в апориях Зенона и в наши дни нельзя считать преодоленными» — считала создательница советской школы философии математики Софья Яновская.10
Апории Зенона не перестают
интересовать и математиков, и физиков,
и философов, и всех тех, кто когда либо
сталкивался с этими парадоксами. Интерес
к апориям не ослабевает в настоящее время
и связан с проблемами научного познания
пространства, времени и движения, а также
с проблемами «начал». Апории Зенона
служили инструментом для достижения
основной цели: доказательство отсутствия
подлинного бытия чувственного мира. Помимо
этого было отчетливо показано, что геометрия
на уровне теории продумана в достаточной
степени глубоко, её краеугольные камни
внутренне несостоятельны и противоречивы. Демонстрация этих примеров Зенона не
смогла убедить более поздних мыслителей
согласиться с выводами Парменида, но
смогла заставить их начать уважать формальную
логику и найти в себе силы увидеть новые
возможности её применения. Ко всему этому
апории заставили их переформулировать
пифагорейские понятия, так, чтобы противоречия
Зенона были исключены. Таким образом,
как из допущения бесконечной делимости
пространства (наличия бесконечного количества
«точек» в любом отрезке), так и из
допущения неделимости отдельных «моментов»
времени Зенон делает один и тот же вывод:
ни множество, ни движение не могут быть
мыслимы непротиворечиво, а посему они
не существуют в действительности, не
являются истинными, а пребывают только
во мнении.
Демонстрация этих примеров Зенона не
смогла убедить более поздних мыслителей
согласиться с выводами Парменида, но
смогла заставить их начать уважать формальную
логику и найти в себе силы увидеть новые
возможности её применения. Ко всему этому
апории заставили их переформулировать
пифагорейские понятия, так, чтобы противоречия
Зенона были исключены. Таким образом,
как из допущения бесконечной делимости
пространства (наличия бесконечного количества
«точек» в любом отрезке), так и из
допущения неделимости отдельных «моментов»
времени Зенон делает один и тот же вывод:
ни множество, ни движение не могут быть
мыслимы непротиворечиво, а посему они
не существуют в действительности, не
являются истинными, а пребывают только
во мнении.
Таким образом, доказав, что движение не может начаться и, более того, не может закончиться, невольно задумываешься о том, что движение как таковое невозможно.
10. Список Литературы:
Список Литературы:
- В.Я. Комарова «Учение Зенона Элейского. Попытка реконструкции системы аргументов». Л., 1988.
- Сидоренко Е. А. Логические выводы доказательства и теория дедукции
- Энциклопедия «Кругосвет» — «Зенон Элейский»
- Комарова В. Я. Учение Зенона Элейского.
- Фролов И. Т. и др. «Введение в Философию»
- Ф. Коплстон «История философии: Древняя Греция и Древний Рим», том 1, М.: «Центр-полиграф», 2003.
- Спиркин А.Г. учебное пособие по философии.
- Сидаренко А.«Древнегреческая философия»
- Манеев А. К. Философский анализ зеноновских апорий.
- Янковская С.А. Методологические проблемы науки.
1 Спиркин А.Г. учебное пособие по философии, стр. 35
2 Манеев А. К. Философский анализ зеноновских апорий. Стр. 12
3 Сидоренко Е. А. «Логические выводы доказательства и теория дедукции» стр. 291, 293
4 Сидаренко А. «Древнегреческая
философия» стр. 12.
«Древнегреческая
философия» стр. 12.
5 В.Я. Комарова «Учение Зенона Элейского. Попытка реконструкции системы аргументов». Л., 1988. Стр.134.
6 Анисов А. «Апории Зенона и проблема движения» Стр. 24
7 Сидаренко А.«Древнегреческая философия» Стр. 14
8 Ф. Коплстон «История философии: Древняя Греция и Древний Рим», стр. 54
9 Фролов И. Т. и др. «Введение в Философию» стр. 215.
10 Янковская С.А. Методологические проблемы науки. Стр. 78
Страница
Апории Зенона
Апори́и Зено́на (от др.-греч. ἀπορία «трудность») — внешне парадоксальные рассуждения на тему о движении и множестве древнегреческого философа Зенона Элейского (V век до н. э.).
Современники упоминали более 40 апорий Зенона, до нас дошли 9, обсуждаемые в «Физике» и в других трудах Аристотеля, а также в комментариях Симпликия, Филопона и Фемистия к Аристотелю[1]; одна апория из этих 9 приводится также у Диогена Лаэртского[2], апории о множестве обсуждаются в диалоге Платона «Парменид».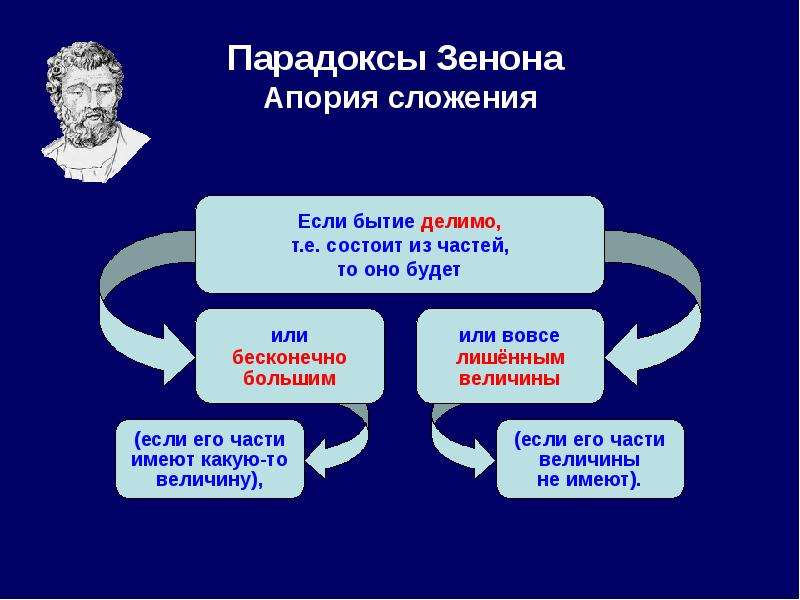 Комментатор Аристотеля Элий Александрийский (VI век) сообщает, что Зенон высказал 40 рассуждений (эпихейрем) о множестве и пять — о движении[3]:
Комментатор Аристотеля Элий Александрийский (VI век) сообщает, что Зенон высказал 40 рассуждений (эпихейрем) о множестве и пять — о движении[3]:
Он составил для своего учителя Парменида, который утверждал, что сущее одно по виду, но множественно согласно очевидности, {аргументацию} из сорока эпихейрем в пользу того, что сущее одно, так как считал, что быть союзником учителя — это хорошо. Ещё как-то, защищая того же учителя, утверждавшего, что сущее неподвижно, он выдвинул пять эпихейрем в пользу того, что сущее неподвижно. Антисфен-киник, который не смог на них возразить, встал и стал ходить, полагая, что доказательство делом сильнее всякого возражения словом.
Наиболее известны парадокс «Ахиллес и черепаха» и другие апории Зенона о движении, которые обсуждаются более двух тысячелетий, им посвящены сотни исследований. Платон в «Пармениде» их не упоминает, поэтому В. Я. Комарова предполагает, что парадоксы движения были написаны Зеноном позднее других[4].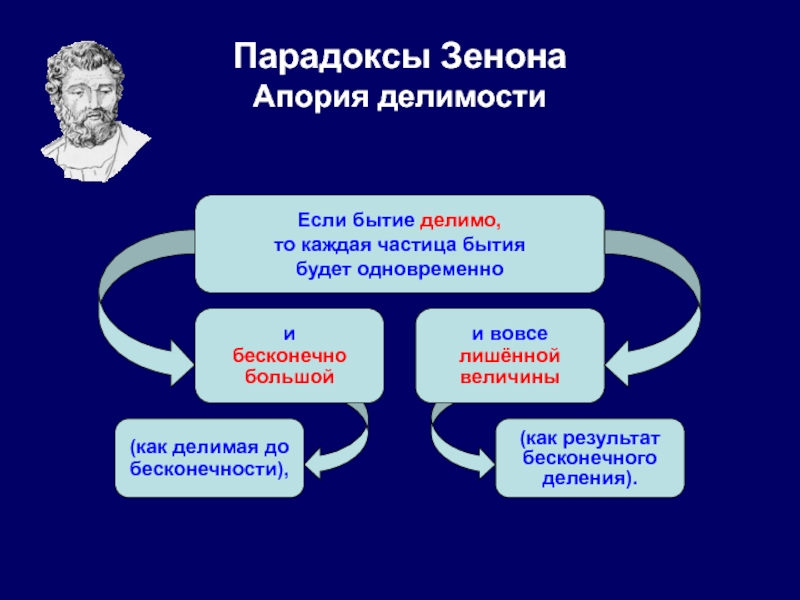
Ошибочно воспринимать эти рассуждения как софизмы или полагать, что с появлением высшей математики все апории разрешены[5]. Бертран Рассел писал, что апории Зенона «в той или иной форме затрагивают основания почти всех теорий пространства, времени и бесконечности, предлагавшихся с его времени до наших дней»[6]. «Проблематика аргументов Зенона далеко выходит за пределы конкретной исторической ситуации, обусловившей их появление. Анализу апорий Зенона посвящена колоссальная литература; особенно большое внимание им уделялось в последние сто лет, когда математики стали усматривать в них предвосхищение парадоксов современной теории множеств»[7]. Научные дискуссии, вызванные рассуждениями Зенона, существенно углубили понимание таких фундаментальных понятий, как роль непрерывного и дискретного (прерывного) в природе, адекватность физического движения и его математической модели и др. Эти дискуссии продолжаются и в настоящее время (см. список литературы), прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось[8].
Философия элеатов
Элейская философская школа (элеаты) существовала в период с конца VI века до н. э. до первой половины V века до н. э., родоначальником её считается Парменид, учитель Зенона. Школа разработала своеобразное учение о бытии. Парменид изложил свои философские взгляды в поэме, от которой до нас дошли отдельные фрагменты[9][10][11].
Элеаты отстаивали единство бытия, считая, что представление о множественности вещей во Вселенной ошибочно[12]. Бытие элеатов полно, реально и познаваемо, однако вместе с тем оно нераздельно, неизменно и вечно, у него нет ни прошлого, ни будущего, ни рождения, ни смерти. Мышление, говорилось в поэме Парменида, по своему содержанию тождественно предмету мышления («одно и то же — мышление и то, о чём мысль»). Далее Парменид логически выводит характеристики истинно сущего: оно «не возникло, не уничтожимо, целокупно [не имеет частей][11], единственно, неподвижно и нескончаемо [во времени]».
Познание этого целостного мира возможно только путём разумных (логических) рассуждений, а чувственная картина мира, включая наблюдаемые движения, обманчива и противоречива[13]. С этих же позиций элеаты впервые в науке поставили вопрос о допустимости научных понятий, связанных с бесконечностью[14].
Как отмечают В. Ф. Асмус и ряд других историков, элеаты отрицали не возможность восприятия движения и множественности мира, а их мыслимость, то есть совместимость с логикой. Элеаты выявляли неизбежные, с их точки зрения, противоречия, возникающие при применении к природе научных понятий того времени, что подтверждало позицию Парменида, рационально-логический подход которого позволял этих противоречий избежать[15][16]. Отстаивая свои взгляды в философских спорах, Зенон и другие элеаты использовали изощрённую логическую аргументацию, и важной её частью были апории Зенона, доказывающие нелогичность и противоречивость взглядов оппонентов.
Апории о движении
Это наиболее известные (и, судя по библиографии, наиболее актуальные) парадоксы Зенона.
Модели движения в античной натурфилософии
Апории и вообще взгляды Зенона нам известны только в кратком пересказе других античных философов, которые жили столетия спустя и хотя высоко ценили Зенона как «основателя диалектики», но чаще всего были его идейными противниками. Поэтому трудно достоверно выяснить, как формулировал апории сам Зенон, что он хотел показать или опровергнуть[17]. Согласно наиболее распространённой точке зрения, идущей от Платона, апории были направлены на защиту монизма философии Парменида от обыденных представлений о движении и множественности вещей; оппонентами Зенона могли быть сторонники здравого смысла. Некоторые учёные считают, что аргументы Зенона были связаны с размышлениями о ранних математических учениях пифагорейцев, поскольку апории фактически ставили под сомнение применение количественных подходов к физическим телам и пространственной протяжённости[8][18][5].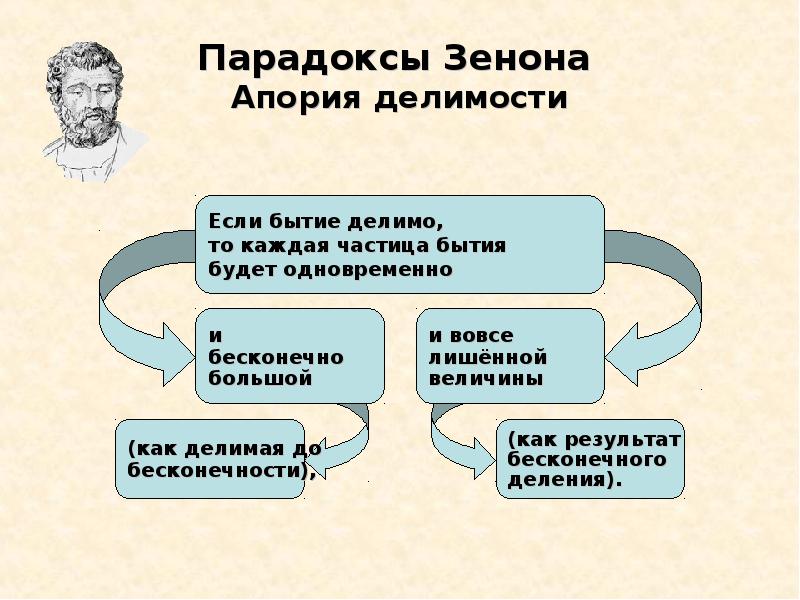 Эта точка зрения подтверждается тем, что элеатов в древности называли афизиками, то есть противниками науки о природе[17].
Эта точка зрения подтверждается тем, что элеатов в древности называли афизиками, то есть противниками науки о природе[17].
В V веке до н. э. древнегреческая математика достигла высокой ступени развития, и пифагорейская школа выражала уверенность, что математические закономерности лежат в основе всех законов природы. В частности, математическая модель движения в природе была создана на основе геометрии, которая к этому времени уже была достаточно глубоко разработана. Геометрия пифагорейцев опиралась на ряд идеализированных понятий: тело, поверхность, фигура, линия — и самым идеализированным было фундаментальное понятие точки пространства, не имеющей никаких собственных измеримых характеристик[19][20]. Тем самым любая классическая кривая считалась одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие не вызывало проблем, но применение этой схемы к реальному движению поставило вопрос, насколько правомерен такой внутренне противоречивый подход[21]. Первым проблему ясно сформулировал Зенон Элейский в серии своих парадоксов (апорий).
Первым проблему ясно сформулировал Зенон Элейский в серии своих парадоксов (апорий).
В двух апориях (Ахиллес и Дихотомия) предполагается, что время и пространство непрерывны и неограниченно делимы; Зенон показывает, что это допущение приводит к логическим трудностям. Третья апория («Стрела»), напротив, рассматривает время как дискретное, составленное из точек-моментов; в этом случае, как показал Зенон, возникают другие трудности[16]. Отметим, что неправильно утверждать, будто Зенон считал движение несуществующим, потому что, согласно элейской философии, доказать несуществование чего бы то ни было невозможно: «несуществующее немыслимо и невыразимо»[22]. Цель аргументации Зенона была более узкой: выявить противоречия в позиции оппонента.
Часто в число апорий движения включают «Стадион» (см. ниже), но по тематике этот парадокс скорее относится к апориям бесконечности. Далее содержание апорий пересказывается с использованием современной терминологии.
Под влиянием возникших философских споров сформировались два взгляда на строение материи и пространства: первый утверждал их бесконечную делимость, а второй — существование неделимых частиц, «атомов». Каждая из этих школ решала поставленные элеатами проблемы по-своему.
Каждая из этих школ решала поставленные элеатами проблемы по-своему.
Содержание апорий о движении
Ахиллес и черепаха
Ахиллес и черепаха — стадии погониДопустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху. |
Здесь и в следующей апории предполагается, что пространство и время не имеют предела делимости. Диоген Лаэртский считал автором этой знаменитой апории Парменида, учителя Зенона[16]. Черепаха как персонаж впервые упоминается у комментатора Симпликия; в тексте парадокса, приведённом у Аристотеля, быстроногий Ахиллес догоняет другого бегуна.
Дихотомия
Чтобы преодолеть путь, нужно сначала преодолеть половину пути, а чтобы преодолеть половину пути, нужно сначала преодолеть половину половины, и так до бесконечности. |
Название «Дихотомия» (по-гречески: деление пополам) дано Аристотелем.
Летящая стрела
Стрела ЗенонаЛетящая стрела неподвижна, так как в каждый момент она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда. |
Апории «Дихотомия» и «Стрела» напоминают следующие парадоксальные афоризмы, приписываемые ведущему представителю древнекитайской «школы имён» (мин цзя) Гунсунь Луну (середина IV века до н. э. — середина III века до н. э.):
- «В стремительном [полёте] стрелы есть момент отсутствия и движения, и остановки».
- «Если от палки [длиной] в один чи ежедневно отнимать половину, это не завершится и через 10000 поколений».
Критика апорий Аристотелем
Лисипп. Бюст Аристотеля (римская копия).Аристотель (IV век до н. э.) считал материю непрерывной и неограниченно делимой. В книгах IV (главы 2, 3), VI (главы 2, 9) и VIII (глава 8) своей «Физики» он анализирует и отвергает рассуждения Зенона[23]. В отношении апорий движения Аристотель подчёркивает, что хотя интервал времени можно неограниченно делить, но его нельзя составить из изолированных точек-моментов и нельзя этой бесконечной делимости соотносить бесконечное время:
В книгах IV (главы 2, 3), VI (главы 2, 9) и VIII (глава 8) своей «Физики» он анализирует и отвергает рассуждения Зенона[23]. В отношении апорий движения Аристотель подчёркивает, что хотя интервал времени можно неограниченно делить, но его нельзя составить из изолированных точек-моментов и нельзя этой бесконечной делимости соотносить бесконечное время:
Зенон же рассуждает неправильно. Если всегда — говорит он — всякое [тело] покоится, когда оно находится в равном [себе месте], а перемещающееся [тело] в момент «теперь» всегда [находится в равном себе месте], то летящая стрела неподвижна. Но это неверно, потому что время не слагается из неделимых «теперь», а также никакая другая величина.
Есть четыре рассуждения Зенона о движении, доставляющие большие затруднения тем, кто пытается их разрешить. Первое — о несуществовании движения на том основании, что перемещающееся [тело] должно дойти до половины прежде, чем до конца.<…> Второе — так называемый «Ахиллес»: оно состоит в том, что самое медленное [существо] никогда не сможет быть настигнуто в беге самым быстрым, ибо преследующему необходимо прежде прийти в место, откуда уже двинулось убегающее, так что более медленное всегда должно будет на какое-то [расстояние] опережать [преследующего].И это рассуждение основывается на делении пополам, отличается же [от предыдущего] тем, что взятая величина делится не на две равные части.<…>
Третье, о котором только что было упомянуто, состоит в том, что летящая стрела стоит неподвижно; оно вытекает из предположения, что время слагается из [отдельных] «теперь»; если это не признавать, силлогизма не получится.
Диоген сообщает, что у Аристотеля и Гераклида Понтийского были сочинения под названием «Против учения Зенона», однако они не сохранились.
Мнения историков и комментаторов по поводу аргументов Аристотеля разделились: одни считали их достаточными, другие критиковали за неубедительность и недостаточную глубину. В частности, Аристотель не дал объяснения, как конечный отрезок времени может состоять из бесконечного числа частей[16]. В. Я. Комарова пишет[24]:
Позиция Аристотеля ясна, но не безупречна — и прежде всего потому, что ему самому не удалось ни обнаружить логические ошибки в доказательствах, ни дать удовлетворительное объяснение парадоксам… Аристотелю не удалось опровергнуть аргументы по той простой причине, что в логическом отношении доказательства Зенона составлены безукоризненно.
Атомистический подход
Эпикур СамосскийПервый древнегреческий атомист, Левкипп, был учеником Зенона и одним из учителей другого крупного атомиста, Демокрита. Наиболее детальное изложение античного атомизма — система Эпикура, IV—III века до н. э. — дошло до нас в изложении Лукреция Кара. В отличие от Аристотеля, Эпикур считал мир дискретным, состоящим из вечно движущихся неделимых атомов и пустоты. Особый интерес представляет эпикуровская концепция изотахии, согласно которой все атомы движутся с одинаковой скоростью[25]. Учитывая, что в мире Эпикура нельзя измерить нечто меньшее, чем атом, отсюда следует, что существует и наименьший измеримый интервал времени. Математическая идеализация этой модели представляла любое тело, фигуру или линию как объединение бесконечного числа бесконечно малых неделимых (этот подход как «метод неделимых» получил особенное развитие в XVI—XVII вв.).
Как следствие, наблюдаемое движение из непрерывного становится скачкообразным..PNG)
Обсуждение в Новое время
Полемика вокруг зеноновских апорий продолжилась и в Новое время. До XVII века интерес к апориям не отмечается, и их аристотелевская оценка являлась общепринятой. Первое серьёзное исследование предпринял французский мыслитель Пьер Бейль, автор известного «Исторического и критического словаря» (1696). В статье о Зеноне Бейль подверг критике позицию Аристотеля и пришёл к выводу, что Зенон прав: понятия времени, протяжённости и движения связаны с трудностями, непреодолимыми для человеческого ума[27].
Сходные с апориями темы затронуты в антиномиях Канта. Гегель в своей «Истории философии» подчеркнул, что Зенонова диалектика материи «не опровергнута до сегодняшнего дня» (ist bis auf heutigen Tag unwiderlegt)[2]. Гегель оценил Зенона как «отца диалектики» не только в античном, но и в гегелевском смысле слова диалектика. Он отметил, что Зенон различает чувственно воспринимаемое и мыслимое движение. Последнее, в соответствии со своей философией, Гегель описал как сочетание и конфликт противоположностей, как диалектику понятий[28]. Гегель не даёт ответа на вопрос, насколько этот анализ приложим к реальному движению, ограничившись выводом: «Зенон осознал определения, содержащиеся в наших представлениях о пространстве и времени, и обнаружил заключающиеся в них противоречия»[29]
Во второй половине XIX века анализом парадоксов Зенона занимались многие учёные, высказывавшие самые разные точки зрения. Среди них[2]:
и многие другие.
Современная трактовка
Довольно часто появлялись (и продолжают появляться) попытки математически опровергнуть рассуждения Зенона и тем самым «закрыть тему». Например, построив ряд из уменьшающихся интервалов для апории «Ахиллес и черепаха», можно легко доказать, что он сходится, так что Ахиллес обгонит черепаху. В этих «опровержениях», однако, подменяется суть спора. В апориях Зенона речь идёт не о математической модели, а о реальном движении, и поэтому бессмысленно ограничить анализ парадокса внутриматематическими рассуждениями — ведь Зенон как раз и ставит под сомнение применимость к реальному движению идеализированных математических понятий[16][31]. О проблеме адекватности реального движения и его математической модели см. следующий раздел данной статьи.
Д. Гильберт и П. Бернайс в монографии «Основания математики» (1934) замечают по поводу апории «Ахиллес и черепаха»[32]:
Обычно этот парадокс пытаются обойти рассуждением о том, что сумма бесконечного числа этих временных интервалов всё-таки сходится и, таким образом, даёт конечный промежуток времени.
Однако это рассуждение абсолютно не затрагивает один существенно парадоксальный момент, а именно парадокс, заключающийся в том, что некая бесконечная последовательность следующих друг за другом событий, последовательность, завершаемость которой мы не можем себе даже представить (не только физически, но хотя бы в принципе), на самом деле всё-таки должна завершиться.
Серьёзные исследования апорий Зенона рассматривают физическую и математическую модели совместно. Р. Курант и Г. Роббинс полагают, что для разрешения парадоксов необходимо существенно углубить наше понимание физического движения[33]. С течением времени движущееся тело последовательно проходит все точки своей траектории, однако если для любого ненулевого интервала пространства и времени нетрудно указать следующий за ним интервал, то для точки (или момента) невозможно указать следующую за ней точку, и это нарушает последовательность. «Остаётся неизбежное расхождение между интуитивной идеей и точным математическим языком, предназначенным для того, чтобы описывать её основные линии в научных, логических терминах. Парадоксы Зенона ярко обнаруживают это несоответствие.»
Парадоксы Зенона ярко обнаруживают это несоответствие.»
Гильберт и Бернайс высказывают мнение, что суть парадоксов состоит в неадекватности непрерывной, бесконечно делимой математической модели, с одной стороны, и физически дискретной материи, с другой[34]: «мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени». Другими словами, парадоксы возникают из-за некорректного применения к реальности идеализированных понятий «точка пространства» и «момент времени», которые не имеют в реальности никаких аналогов, потому что любой физический объект имеет ненулевые размеры, ненулевую длительность и не может быть делим бесконечно.
Близкие точки зрения можно найти у Анри Бергсона и у Николя Бурбаки. Согласно Анри Бергсону[35]:
Противоречия, на которые указывает школа элеатов, касаются не столько самого движения как такового, сколько того искусственного преобразования движения, которое совершает наш разум.
Бергсон полагал, что есть принципиальная разница между движением и пройденным расстоянием. Пройденное расстояние можно произвольно делить, между тем как движение произвольному делению не поддаётся. Каждый шаг Ахиллеса и каждый шаг черепахи должны рассматриваться как неделимые. Это же относится и к полёту стрелы:
Истина заключается в том, что если стрела выходит из точки А и попадает в точку В, то её движение АВ так же просто, так же неразложимо — поскольку это есть движение, — как напряжение пускающего её лука.
— Бергсон А. Творческая эволюция. Глава четвёртая. Кинематографический механизм мышления и механистическая иллюзия. Взгляд на историю систем, реальное становление и ложный эволюционизм
Согласно Николя Бурбаки[36]:
Вопрос о бесконечной делимости пространства (бесспорно, поставленный ещё ранними пифагорейцами) привёл, как известно, к значительным затруднениям в философии: от Элеатов до Больцано и Кантора математики и философы не в силах были разрешить парадокса — как конечная величина может состоять из бесконечного числа точек, не имеющих размера.
Замечание Бурбаки означает, что необходимо объяснить: каким образом физический процесс за конечное время принимает бесконечно много различных состояний. Одно из возможных объяснений: пространство-время в действительности является дискретным, то есть существуют минимальные порции (кванты) как пространства, так и времени[37]. Если это так, то все парадоксы бесконечности в апориях исчезают. Ричард Фейнман заявил[38]:
Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что [в квантовой механике] она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны.
Дискретное пространство-время активно обсуждалось физиками ещё в 1950-е годы — в частности, в связи с проектами единой теории поля[39], — однако существенного продвижения по этому пути добиться не удалось.
С. А. Векшенов считает, что для решения парадоксов необходимо ввести числовую структуру, более соответствующую интуитивно-физическим представлениям, чем канторовский точечный континуум[40]. Пример неконтинуальной теории движения предложил Садэо Сирайси[41].
Морис Клайн в своих комментариях по поводу апорий Зенона пишет: «Важно отчётливо сознавать, что природа и математическое описание природы — не одно и то же, причём различие обусловлено не только тем, что математика представляет собой идеализацию… Природа, возможно, отличается несравненно большей сложностью, или структура её не обладает особой правильностью»[42].
«Математический энциклопедический словарь» считает, что сущность апорий достаточно глубока, и рассматривает разные пути решения проблемы[43]:
Можно оспаривать удобство или адекватность реальному движению общеупотребительной математической модели. Для исследования концепции физических бесконечно малых и бесконечно больших величин неоднократно предпринимались попытки построения теории действительных чисел, в которой аксиома Архимеда не имеет места.
Во всяком случае, теория неархимедовых упорядоченных полей является весьма содержательной частью современной алгебры.
Следующий раздел данной статьи содержит более подробное изложение этой темы.
Адекватность аналитической теории движения
Общая теория движения с переменной скоростью была разработана в конце XVII века Ньютоном и Лейбницем. Математической основой теории служит математический анализ, первоначально опиравшийся на понятие бесконечно малой величины. В дискуссии о том, что собой представляет бесконечно малая, вновь возродились два античных подхода[44][45].
- Первый подход, которого придерживался Лейбниц, доминировал весь XVIII век. Аналогично античному атомизму, он рассматривает бесконечно малые как особый вид чисел (больше нуля, но меньше любого обычного положительного числа). Строгое обоснование этого подхода (так называемый нестандартный анализ) разработал Абрахам Робинсон в XX веке. Основой анализа по Робинсону служит расширенная числовая система (гипервещественные числа).
 Конечно, робинсоновские бесконечно малые мало похожи на античные атомы хотя бы потому, что они неограниченно делимы, но они позволяют корректно рассматривать непрерывную кривую во времени и пространстве как состоящую из бесконечного количества бесконечно малых участков.
Конечно, робинсоновские бесконечно малые мало похожи на античные атомы хотя бы потому, что они неограниченно делимы, но они позволяют корректно рассматривать непрерывную кривую во времени и пространстве как состоящую из бесконечного количества бесконечно малых участков. - Второй подход предложил Коши в начале XIX века. Его анализ построен на обычных вещественных числах, а для анализа непрерывных зависимостей используется понятие предела. Сходного мнения на обоснование анализа придерживались Ньютон, Д’Аламбер и Лагранж, хотя были в этом мнении не всегда последовательны.
Оба подхода практически эквивалентны, но с точки зрения физики удобнее первый; в учебниках физики часто встречаются фразы вроде «пусть dV — бесконечно малый объём…». С другой стороны, вопрос о том, какой из подходов ближе к физической реальности, не решён. При первом подходе неясно, чему соответствуют в природе бесконечно малые числа. При втором адекватности физической и математической модели мешает тот факт, что операция перехода к пределу — инструментальный исследовательский приём, не имеющий никакого природного аналога. В частности, трудно говорить о физической адекватности бесконечных рядов, элементы которых относятся к произвольно малым интервалам пространства и времени (хотя как приближённая модель реальности такие модели часто и успешно используются)[5][46]. Наконец, не доказано, что время и пространство устроены сколько-нибудь похоже на математические структуры вещественных или гипервещественных чисел[40].
В частности, трудно говорить о физической адекватности бесконечных рядов, элементы которых относятся к произвольно малым интервалам пространства и времени (хотя как приближённая модель реальности такие модели часто и успешно используются)[5][46]. Наконец, не доказано, что время и пространство устроены сколько-нибудь похоже на математические структуры вещественных или гипервещественных чисел[40].
Дополнительную сложность внесла в вопрос квантовая механика, показавшая, что в микромире резко повышена роль дискретности. Таким образом, дискуссии о структуре пространства, времени и движения, начатые Зеноном, активно продолжаются и далеки от завершения.
Другие апории Зенона
Вышеприведённые (наиболее известные) апории Зенона касались применения понятия бесконечности к движению, пространству и времени. В других апориях Зенон демонстрирует иные, более общие аспекты бесконечности. Однако, в отличие от трёх знаменитых апорий о физическом движении, другие апории изложены менее ясно и касаются в основном чисто математических или общефилософских аспектов. С появлением математической теории бесконечных множеств интерес к ним существенно упал.
С появлением математической теории бесконечных множеств интерес к ним существенно упал.
Стадион
Апория «Стадион» (или «Ристалище») у Аристотеля («Физика», Z, 9) сформулирована не вполне ясно:
Четвертый [аргумент] — о равных телах, движущихся по стадиону в противоположных направлениях параллельно равных [им тел]; одни [движутся] от конца стадия, другие — от середины с равной скоростью, откуда, как он думает, следует, что половина времени равна двойному.
Исследователи предлагали разные истолкования этой апории. Л. В. Блинников сформулировал её следующим образом[47]:
Два тела движутся навстречу друг другу. В этом случае одно из них затратит на прохождение мимо другого столько же времени, сколько оно затратило бы на прохождение мимо покоящегося. Значит, половина равна целому. |
С. А. Яновская предлагает иное истолкование, основанное на атомистических предпосылках[48]:
Пусть время состоит из неделимых протяженных атомов.
Представим себе на противоположных концах ристалища двух бегунов, настолько быстрых, что на пробег от одного до другого конца ристалища каждому из них требуется один только атом времени. И пусть оба одновременно выбегают с противоположных концов. Когда произойдет их встреча, неделимый атом времени разделится пополам, то есть в атомы времени тела не могут двигаться, как это и было предположено в апории «Стрела».
По другим интерпретациям, идея этой апории аналогична парадоксу Галилея или «колесу Аристотеля»: бесконечное множество может быть равномощно своей части[49].
Множественность
Часть апорий посвящена обсуждению вопроса о единстве и множественности мира[17].
Если их [существующих вещей] много, то их должно быть столь много, сколько их есть, — не больше и не меньше. А если их столь много, сколько их есть, то их [число] ограничено. [Но] если существующих [вещей] много, то их [число] неограничено: ибо всегда существуют другие вещи между существующими [вещами], и снова другие между ними. |
Сходные вопросы обсуждаются в диалоге Платона «Парменид»[50], где Зенон и Парменид обстоятельно разъясняют свою позицию. На современном языке данное рассуждение Зенона означает[17], что множественное бытие не может быть актуально бесконечно и поэтому должно быть конечно, но к существующим вещам всегда можно добавить новые, что противоречит конечности. Вывод: бытие не может быть множественным.
Комментаторы обращают внимание на то, что данная апория по своей схеме чрезвычайно напоминает открытые на рубеже XIX—XX веков антиномии теории множеств[17][51], особенно парадокс Кантора: с одной стороны, мощность множества всех множеств больше, чем мощность любого другого множества, но с другой стороны, для любого множества нетрудно указать множество большей мощности (теорема Кантора). Это противоречие, вполне в духе апории Зенона, разрешается однозначно: абстракция множества всех множеств признаётся недопустимой и несуществующей как научное понятие.
Мера
Симпликий описывает эту апорию следующим образом[14].
Доказав, что, «если вещь не имеет величины, она не существует», Зенон прибавляет: «Если вещь существует, необходимо, чтобы она имела некоторую величину, некоторую толщину и чтобы было некоторое расстояние между тем, что представляет в ней взаимное различие». То же можно сказать о предыдущей, о той части этой вещи, которая предшествует по малости в дихотомическом делении. Итак, это предыдущее должно также иметь некоторую величину и своё предыдущее. Сказанное один раз можно всегда повторять. Таким образом, никогда не будет крайнего предела, где не было бы различных друг от друга частей. Итак, если есть множественность, нужно, чтобы вещи были в одно и то же время велики и малы и настолько малы, чтобы не иметь величины, и настолько велики, чтобы быть бесконечными… У чего нет совершенно ни величины, ни толщины, ни объёма, того и вовсе нет. |
Другими словами, если деление вещи пополам сохраняет её качество, то в пределе получаем, что вещь одновременно и бесконечно велика (поскольку неограниченно делима), и бесконечно мала. Кроме того, непонятно, как существующая вещь может иметь бесконечно малые измерения.
Кроме того, непонятно, как существующая вещь может иметь бесконечно малые измерения.
Более подробно эти же аргументы присутствуют в комментариях Филопона[52]. Также аналогичные рассуждения Зенона цитирует и критикует Аристотель в своей «Метафизике»[53]:
Если само-по-себе-единое неделимо, то, согласно положению Зенона, оно должно быть ничем. В самом деле, если прибавление чего-то к вещи не делает её больше и отнятие его от неё не делает её меньше, то, утверждает Зенон, это нечто не относится к существующему, явно полагая, что существующее — это величина, а раз величина, то и нечто телесное: ведь телесное есть в полной мере сущее; однако другие величины, например плоскость и линия, если их прибавлять, в одном случае увеличивают, а в другом нет; точка же и единица не делают этого никаким образом. А так как Зенон рассуждает грубо и так как нечто неделимое может существовать, и притом так, что оно будет некоторым образом ограждено от Зеноновых рассуждений (ибо если такое неделимое прибавлять, оно, правда, не увеличит, но умножит), то спрашивается, как из одного такого единого или нескольких получится величина? Предполагать это — всё равно что утверждать, что линия состоит из точек.
О месте
В изложении Аристотеля апория утверждает: если всё существующее помещается в известном пространстве (месте, греч. топос), то ясно, что будет и пространство пространства, и так идёт в бесконечность[54]. Аристотель замечает на это, что место не есть вещь и не нуждается в собственном месте. Данная апория допускает расширенное толкование, поскольку элеаты не признавали пространство отдельно от тел, в нём расположенных, то есть отождествляли материю и пространство, ею занимаемое[16]. Хотя Аристотель и отвергает рассуждение Зенона, но в своей «Физике» он приходит по существу к тому же выводу, что и элеаты: место существует лишь относительно тел, в нём находящихся. При этом Аристотель обходит молчанием естественный вопрос, как происходит изменение места при движении тела[55].
Медимн зерна
Каждое отдельное зерно падает на землю бесшумно. Тогда отчего медимн (большой мешок) зерна падает с шумом?[56] |
Формулировка Зенона подвергалась критике, так как парадокс легко объясняется ссылкой на порог восприятия звука — отдельное зерно падает не бесшумно, а очень тихо, поэтому звука падения не слышно. Смысл апории — доказать, что часть не подобна целому (качественно отличается от него) и, следовательно, бесконечная делимость невозможна[57]. Аналогичные парадоксы предложил в IV веке до н. э. Евбулид — парадоксы «Лысый» и «Куча»: «одно зерно — не куча, добавление одного зерна не меняет дела, с какого же количества зёрен начинается куча?»
Смысл апории — доказать, что часть не подобна целому (качественно отличается от него) и, следовательно, бесконечная делимость невозможна[57]. Аналогичные парадоксы предложил в IV веке до н. э. Евбулид — парадоксы «Лысый» и «Куча»: «одно зерно — не куча, добавление одного зерна не меняет дела, с какого же количества зёрен начинается куча?»
Историческое значение апорий Зенона
«Зенон вскрыл противоречия, в которые впадает мышление при попытке постигнуть бесконечное в понятиях. Его апории — это первые парадоксы, возникшие в связи с понятием бесконечного»[14]. Чёткое различение потенциальной и актуальной бесконечности у Аристотеля — во многом результат осмысления зеноновских апорий. Другие исторические заслуги элейских парадоксов:
- «Рассуждения Зенона, изложенные точной и ясной прозой, являются первым в истории примером чисто логических доказательств. Именно этим определяется исключительно важное место Зенона в истории науки»[58].
 Рассуждения по аналогии и поэтические фантазии, характерные для философов предыдущего поколения, сменились строгой дедуктивной логикой.
Рассуждения по аналогии и поэтические фантазии, характерные для философов предыдущего поколения, сменились строгой дедуктивной логикой. - Ясное указание на то, что наше представление о реальности (включая математическое) может быть неадекватно этой реальности[59]; в последующем наука столкнулась с многочисленными примерами справедливости этого тезиса.
- Констатация того факта, что разделение непрерывности на отдельные точки (моменты), то есть смешение непрерывности и дискретности, есть противоречие[7].
Как уже отмечалось выше, формирование античного атомизма было попыткой дать ответ на вопросы, поставленные апориями. В дальнейшем к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса, но сам факт непрерывного живого интереса к древней проблеме показывает её эвристическую плодотворность.
Различные точки соприкосновения апорий Зенона с современной наукой обсуждаются в статье Зураба Силагадзе[46]. В заключении этой статьи автор приходит к выводу:
В заключении этой статьи автор приходит к выводу:
Проблемы, поставленные два с половиной тысячелетия назад и с тех пор многократно изученные, до сих пор не исчерпаны. Парадоксы Зенона затрагивают фундаментальные аспекты реальности — локализацию, движение, пространство и время. Время от времени обнаруживаются новые и неожиданные грани этих понятий, и каждое столетие находит полезным снова и снова возвращаться к Зенону. Процесс достижения их окончательного разрешения представляется бесконечным, и наше понимание окружающего мира всё ещё неполно и фрагментарно.
Апории Зенона в литературе и искусстве
А. С. Пушкин посвятил парадоксам Зенона стихотворение «Движение» (1825)[60].
Движенья нет, сказал мудрец брадатый. |
В этом историческом анекдоте «мудрец брадатый» — это сторонник Зенона (комментатор Элий, как сказано выше, приписывал аргументацию самому Зенону[3]), а его оппонентом в разных вариантах анекдота выступает Диоген или Антисфен (оба они жили существенно позднее Зенона, так что с ним самим спорить не могли). Одна из версий анекдота, упоминаемая Гегелем, сообщает, что когда элеат признал аргумент Диогена убедительным, Диоген побил его палкой за чрезмерное доверие к очевидности[61].
Льюис Кэрролл написал диалог с логическими загадками под названием «Что Черепаха сказала Ахиллесу?»[62].
Лев Толстой в III томе эпопеи «Война и мир» (начало 3-й части) пересказывает парадокс про Ахиллеса и черепаху и предлагает своё толкование: нельзя разделять непрерывное движение на «отдельные единицы», вместо этого надо использовать аппарат суммируемых «бесконечно-малых величин». Далее Толстой замечает: «в отыскании законов исторического движения происходит совершенно то же» и критикует попытки рассматривать непрерывный ход истории как происходящий по произволу отдельных влиятельных исторических лиц или сводить историю к отдельным крупным историческим событиям.
Поль Валери в поэме «Кладбище у моря» (Le Cimetiere Marin, 1920) писал[63]:
Зенон Элейский, мыслию разящий, |
В основе сюжета фантастического рассказа Ф. Дика «О неутомимой лягушке» лежит апория «Дихотомия».
Апория про Ахиллеса неоднократно упоминается в произведениях Борхеса. Парадоксальная ситуация, описанная в ней, нашла также отражение в различных юмористических произведениях. Такэси Китано в 2008 году снял фильм «Ахиллес и черепаха».
См. также
Примечания
- ↑ История математики, 1970, с. 90.
- ↑ 1 2 3 Маковельский А. О., 1999, часть 14.
- ↑ 1 2 Фрагменты ранних греческих философов, 1989, с.
 302.
302. - ↑ Комарова, 1988, с. 15-16.
- ↑ 1 2 3 Яновская С. А., 1963, с. 116-118.
- ↑ Ивин А. А. По законам логики. — М.: Молодая гвардия, 1983. — 208 с. — («Эврика»). Архивированная копия (неопр.) (недоступная ссылка). Дата обращения: 7 марта 2010. Архивировано 19 ноября 2007 года.
- ↑ 1 2 Рожанский И. Д. Античная наука. — М.: Наука, 1980. — С. 52. — 198 с. — (История науки и техники).
- ↑ 1 2 Большая советская энциклопедия // Апория.
- ↑ Парменид / А. В. Лебедев // Новая философская энциклопедия : в 4 т. / пред. науч.-ред. совета В. С. Стёпин. — 2-е изд., испр. и доп. — М. : Мысль, 2010. — 2816 с.
- ↑ Элейская школа / А. В. Лебедев // Новая философская энциклопедия : в 4 т.
 / пред. науч.-ред. совета В. С. Стёпин. — 2-е изд., испр. и доп. — М. : Мысль, 2010. — 2816 с.
/ пред. науч.-ред. совета В. С. Стёпин. — 2-е изд., испр. и доп. — М. : Мысль, 2010. — 2816 с. - ↑ 1 2 Рожанский И. Д. Ранняя греческая философия // Фрагменты ранних греческих философов
- ↑ Маковельский А. О., 1999, часть 16.
- ↑ Лосев А. Ф. Зенон Элейский // Философская энциклопедия. — М.: Советская энциклопедия, 1962. — Т. 2.
- ↑ 1 2 3 Гайденко П. П., 1980.
- ↑ Асмус В. Ф. Элейская школа // Античная философия. — М.: Высшая школа, 2005. — 408 с. — ISBN 5-06-003049-0.
- ↑ 1 2 3 4 5 6 Маковельский А. О., 1999, часть 15.
- ↑ 1 2 3 4 5 Апории Зенона (Философская энциклопедия), 1962.
- ↑ Zeno of Elea // Stanford Encyclopedia of Philosophy.
- ↑ Комарова, 1988, с. 50-52.
- ↑ Диоген Лаэртский. Жизнь, учения и изречения знаменитых философов, глава «Пифагор».
- ↑ Кузнецов Б. Г., 1961, с. 18—20.
- ↑ Комарова, 1988, с. 21.
- ↑ «Физика» Аристотеля.
- ↑ Комарова, 1988, с. 29-30.
- ↑ Кузнецов Б. Г., 1961, с. 38.
- ↑ Лурье С. Очерки из истории античной науки. — М.—Л.: Изд. АН СССР, 1947. — С. 181. — 403 с.
- ↑ Комарова, 1988, с. 31-35.
- ↑ Комарова, 1988, с. 35-41.
- ↑ Гегель Г. В. Ф. Сочинения в 14 тт. — М.: Соцэкгиз, 1959. — Т. IX. — С. 244.
- ↑ Таннери П. Первые шаги древнегреческой науки. — СПб., 1902.
- ↑ Papa-Grimaldi, Alba. Why Mathematical Solutions of Zeno’s Paradoxes Miss the Point: Zeno’s One and Many Relation and Parmenides’ Prohibition (неопр.). The Review of Metaphysics. Дата обращения: 17 августа 2011. Архивировано 28 августа 2011 года.
- ↑ Гильберт Д., Бернайс П. Основания математики. Логические исчисления и формализация арифметики. — М., 1979. — С. 40.
- ↑ Курант Р., Роббинс Г. Что такое математика. — 3-е изд. — М.: МЦНМО, 2001. — С. 353. — 568 с. — ISBN 5-900916-45-6.
- ↑ История математики, 1970, с. 93.
- ↑ Цит. по: Данциг, Тобиас. Числа — язык науки. — М.: Техносфера, 2008. — С. 111. — ISBN 978-5-94836-172-7.
- ↑ Николя Бурбаки. Архитектура математики. Очерки по истории математики. — М.: Иностранная литература, 1963. — С. 38.
- ↑ van Bendegem, Jean Paul. Discussion:Zeno’s Paradoxes and the Tile Argument // Philosophy of Science. — Belgium, 1987. — Т. 54. — С. 295—302.
- ↑ Фейнман Р. Характер физических законов. — Изд. 2-е. — М.: Наука, 1987. — С. 152—153. — 160 с. — (Библ. Квант, выпуск 62).
- ↑ Кузнецов Б. Г. Эйнштейн. Жизнь. Смерть. Бессмертие. — 5-е изд., перераб. и доп. — М.: Наука, 1980. — С. 368—374.
- ↑ 1 2 Векшенов, 2008.
- ↑ Shiraishi, 1954.
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 401—402. Архивированная копия (неопр.) (недоступная ссылка). Дата обращения: 15 марта 2010. Архивировано 12 февраля 2007 года.
- ↑ Драгалин А. Г. Антиномия // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 73—75. — 847 с.
- ↑ Успенский В. А. Что такое нестандартный анализ. — М.: Наука, 1987.
- ↑ Гайденко П. П. Понятие времени и проблема континуума (неопр.). Дата обращения: 10 января 2011.
- ↑ 1 2 Silagadze, Z. K. Zeno meets modern science (англ.). Дата обращения: 30 декабря 2010. Архивировано 14 августа 2011 года.
- ↑ Блинников Л. В. Краткий словарь философских персоналий (неопр.). Дата обращения: 30 апреля 2010.
- ↑ Яновская С. А., 1963, с. 127.
- ↑ Богомолов С. А. Актуальная бесконечность (Зенон Элейский, Ис. Ньютон, Г. Кантор). — Л.—М.: ОНТИ, 1934. — С. 53. — 78 с.
- ↑ Парменид, 1968—1972.
- ↑ Zeno’s Paradoxes, Stanford Encyclopedia of Philosophy.
- ↑ Зенон Элейский (неопр.). — Энциклопедия Кругосвет. Дата обращения: 30 декабря 2010. Архивировано 14 августа 2011 года.
- ↑ Аристотель. Метафизика, книга I, глава IV.
- ↑ Аристотель. Физика, IV, 1, 209а.
- ↑ Комарова, 1988, с. 124-129.
- ↑ Ивин А. А. Логика. Учебное пособие, глава 7.
- ↑ Комарова, 1988, с. 122-124.
- ↑ Фрагменты ранних греческих философов, 1989, с. 27.
- ↑ История математики, 1970, с. 89.
- ↑ ДВИЖЕНИЕ.
- ↑ Кузнецов Б. Г., 1961, с. 19.
- ↑ Кэрролл, Льюис. Двухчастная инвенция, или Что черепаха сказала Ахиллесу // Знание — сила. — 1991. — № 9. — С. 6—12.
- ↑ Валери, Поль. Кладбище у моря.
Литература
Античные авторы
Книги современных авторов
- Асмус В. Ф. История античной философии. — М.: Высшая школа, 1965. — С. 40—45.
- Гайденко П. П. Эволюция понятия науки (становление и развитие первых научных программ). Глава «ЭЛЕЙСКАЯ ШКОЛА И ПЕРВАЯ ПОСТАНОВКА ПРОБЛЕМЫ БЕСКОНЕЧНОСТИ» и далее. — М.: Наука, 1980. Архивная копия от 21 декабря 2016 на Wayback Machine
- История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 88—93.
- Комарова В. Я. Учение Зенона Элейского: попытка реконструкции системы аргументов // Вестник ЛГУ. — Л., 1988.
- Кузнецов Б. Г. История философии для физиков и математиков. — М.: Наука, 1974. — 352 с. — (История мировой культуры). — 20 000 экз.
- Кузнецов Б. Г. Эволюция картины мира. — 1-е изд. (2-е издание: УРСС, 2010). — М.: Издательство АН СССР, 1961. — 352 с. — (Из наследия мировой философской мысли: философия науки). — ISBN 978-5-397-01479-3.
- Маковельский А. О. Досократики. В 3 томах. — Минск: Харвест, 1999. — 784 с. — (Классическая философская мысль).
- Смородинов Р. А. Философия последовательного сомнения. — Волгоград: Принт, 2006. — С. 41—68.
- Grünbaum A. Modern science and Zeno’s Paradoxes. — Allen & Unwin, 1968. — 153 p. — ISBN 978-0045130047.
- Guénon R. Les Principes du Calcul infinitésimal. — Gallimard, 1946 и многочисленные переиздания. — «Принципы вычисления бесконечно малых».
- Salmon W. C. (editor). Zeno’s paradoxes. — 2nd ed. — Indianapolis: Hackett Publishing Co. Inc., 2001. — 320 p. — ISBN 978-0872205604.
Краткая библиография научных статей с анализом апорий
Литература перечислена в хронологическом порядке.
- Сватковский В. П. Парадокс Зенона о летящей стреле // Журнал Министерства народного просвещения. — 1888. — № 4 отд. 5. — С. 203—239.
- Херсонский Н. Х. У истоков теории познания. По поводу аргументов Зенона против движения // Журнал Министерства народного просвещения. — 1911. — № XXXIV (август) отд. 2. — С. 207—221.
- Больцано Б. Парадоксы безконечнаго. — Одесса, 1911.
- Богомолов С. А. Аргументы Зенона Элейского при свете учения об актуальной бесконечности // Журнал Министерства народного просвещения. — 1915, новая серия. — № LVI (апрель). — С. 289—328.
- Дмитриев Г. Еще раз о парадоксе Зенона «Ахиллес и черепаха» и путанице В.Фридмана // Под знаменем марксизма. — 1928. — № 4.
- Богомолов С. А. Актуальная бесконечность: Зенон Элейский, Исаак Ньютон и Георг Кантор. — Л.-М., 1934.
- Яновская С. А. Апории Зенона // Философская энциклопедия. — М.: Советская энциклопедия, 1962. — Т. 2.
- Яновская С. А. Преодолены ли в современной науке трудности, известные под названием «апории Зенона»? // Проблемы логики. — М., 1963. — С. 116—136.
- Богомолов А. С. «Летящая стрела» и закон противоречия // Философские науки. — 1964. — № 6.
- Нарский И. С. К вопросу об отражении диалектики движения в понятиях: (ещё раз о парадоксе «Летящая стрела») // Формальная логика и методология науки. — М., 1964. — С. 3—51.
- Цехмистро И. З. Апории Зенона глазами XX века (рус.) // Вопросы философии. — 1966. — № 3.
- Панченко А. И. Апории Зенона и современная философия (рус.) // Вопросы философии. — 1971. — № 7.
- Манеев А. К. Философский анализ зеноновских апорий. — Минск, 1972.
- Кузнецов Г. А. Непрерывность и парадоксы Зенона «Ахиллес» и «Дихотомия» // Теория логического вывода. — М.: Наука, 1973.
- Смоленов Х. Апории Зенона как эвристики атомизма и диалектики // Логико-методологический анализ научного знания. — М., 1979. — С. 76—90.
- Широков В. С. Жан Буридан об апориях Зенона // Философские науки. — 1982. — № 4. — С. 94—101.
- Койре А. Заметки о парадоксах Зенона // Очерки истории философской мысли. О влиянии философских концепций на развитие научных теорий. — М.: Прогресс, 1985.
- Солодухина А. О. Решил ли Айдукевич апорию Зенона «Стрела»? // Научная конференция «Современная логика: проблемы теории, истории и применения в науке». — СПб., 1996.
- Анисов А. М. Апории Зенона и проблема движения // Труды научно-исследовательского семинара Логического центра ИФ РАН, вып. XIV. — М., 2000. — С. 139—155.
- Смирнов А. В. Соизмеримы ли основания рациональности в разных философских традициях? Сравнительное исследование зеноновских апорий и учений раннего калама // Сравнительная философия. — М., 2000. — С. 167—212.
- Вилесов Ю. В. Апории Зенона и соотношение неопределенностей Гейзенберга // Вестник МГУ, серия 7 (философия). — М., 2002. — № 6. — С. 20—28. Архивировано 9 ноября 2019 года.
- Векшенов С. А. Математика и физика пространственно-временного континуума // Основания физики и геометрии. — М.: Издательство Российского университета дружбы народов, 2008. — С. 89—118. Архивировано 13 мая 2012 года.
- Shiraishi, Sadeo. The structure of the continuity of psychological experiences and the phisical world // The science of thought. — Tokyo, 1954. — № 1. — P. 12—24.
- Chambers, Connor J. Zeno of Elea and Bergson’s Neglected Thesis // Journal of the History of Philosophy. — 1974. — Vol. 12, № 1 (January). — P. 63—76.
- Vlastos G. A. Plato’s testimony concerning Zeno of Elea // Journal of the History of Ideas (New York. — 1975. — Vol. XLV. — P. 136—162.
- Vlastos G. A. A note of Zeno’s arrow // Phronesis. — 1996. — Vol. XI. — P. 3—18.
- Smirnov A. Do the Fundamentals of Rationality in Different Philosophical Traditions Correspond? A comparative study of Zeno’s paradoxes and teachings of early Kalām // Islam — West Philosophical Dialogue: the papers presented at the World Congress on Mulla Sadra (1999). — Tehran: Sadra Islamic Philosophy Research Institute, 2004. — P. 109—120.
Ссылки
Объяснение апорий (краткое определение философии от Платона до Деррида)
Лучшее определение Апории на греческом — «трудность». Апория — термин в философской традиция, которая указывает на непреодолимое противоречие, которое заканчивается неразрешимый конфликт (Poros = путь; A poros = отсутствие пути). Апория как понятие повторяется в постструктуралистская критика. Философ Жак Деррида рассматривает апорию как парадоксальный термин, учение которого состоит в блокировании самой способности двигаться. между границами, чтобы определить, сформулировать.Апория — это «нет», слепое пятно, закрывающее поле зрения; Сложность в метафизическом определении того, что есть.
Аристотель определяет апорию как равенство, созданное между двумя противоречивые аргументы. У Платона Апория появляется как часть сократовской прием, призванный подвести собеседника к осознанию его невежество: с позиции временного невежества можно представить альтернативная позиция, ведущая к правильному пути. диалектика дух, по волне, выходит из тупика противоречия между тезисом и антитезисом к преодолению — синтез.Постгегелевская традиция продолжает эту линию мышления и даже радикализирует ее. Теперь Апория отмечает субъективное место противоречия, из которого оно не вытекает. можно двигаться к диалектическому «преодолению» (Aufhebung).
В постструктуралистской мысли Апория обозначает тупик в мышлении, призывая к переформулировке заданных вопросов. Таким образом, для Например, Хайдеггер пытается преодолеть апорию бинарного объекта / предметного контраста, предлагая третий термин, Dasein, что означает быть там , «быть (я) в мире.» Это условие не устраняет полностью афорию; Он не заменяет его на новая запись. У Деррида этот термин используется для описания распада знак, то есть размывание смысла. В его книга Aporias (1993) он определяет Апорию как «ничью землю», где невозможность пересечь становится неспособностью создать формацию, структуру, проект или маркировку границы.
Примеры апорийных вопросов с использованием иллюстрированных книг
Интуитивный ум — это священный дар, а рациональный ум — верный слуга.Мы создали общество, которое чтит слугу и забыло дар. – Альберт Эйнштейн
Апория
Когда рациональность подводит нас, мы озадачены и остаемся с чувством апории (απορια), что означает замешательство или изумление . Мы «в растерянности», в недоумении. Многие диалоги Платона оставляют нас с этим чувством апории. В философии апория относится к философской загадке или кажущемуся неразрешимым тупику в исследовании.То, что мы думали, что знали, мы должны признать, что не знаем — рационально. С другой стороны, в процессе мы могли развить более глубокое чувство любви (в платоновском Symposium ) или мужества (в платоновском Laches ).
Апория с детьми
В моих философских дискуссиях с младшими школьниками я использую вопросы не только для того, чтобы выявить скрытые предположения, которые могут быть у детей, но и чтобы привести их в состояние апории – замешательства, места «незнания».«Если некоторые дети предполагают, что быть смелым — значит быть бесстрашным, я не только спрашиваю, почему они так считают, но и продолжаю спрашивать, как же нас можно назвать смелыми, если мы не боимся? Чего тут храбриться? Этим вопросом я пытаюсь привести детей в состояние «апории». Итак, как вы думаете, как решить головоломный вопрос? Это вызывает любопытство.
Пределы рационального мышления
Восточная философия пытается дать нам более глубокое понимание реальности, показывая также пределы рационального мышления.Дзенский коан звука хлопка в ладоши должен вести учеников к просветлению. Там, где разум упирается в стену, может появиться более глубокое понимание.
Часто мы пытаемся заменить глубокие размышления знаниями. Чем больше я знаю, тем меньше мне приходится думать. У меня есть ответы, поэтому мне не приходится жить в мире неуверенности, двусмысленности, растерянности или «растерянности». Однако именно здесь может начаться истинное мышление: N и что?
Когда мы «в растерянности», мы склонны искать совета у «эксперта».Кажется, наше собственное мышление подвело нас. Но в философских беседах с детьми апория дает им возможность думать.
Удивление расширяет возможности мышления. В «Путешествии по Вселенной » Брайана Томаса Свимма и Мэри Эвелин Такер они заявляют: «Это чувство чуда — один из наших самых ценных проводников в этом продолжающемся путешествии в наше будущее в качестве полноценных людей . И продолжайте с тем, что «Чудо — это ворота, через которые вселенная вливается и поселяется внутри нас.(стр. 113, курсив мой).
Чудо захватывает нас и связывает с окружающим миром. Когда мы «занимаемся» философией с детьми, это чувство удивления расширяется. И, как предполагают Свимм и Такер, «что, если бы после ста миллионов лет существования млекопитающих появился вид, который мог бы оставаться спонтанным, любопытным, изумленным, вынужденным пробовать все? Что тогда произойдет?» (стр. 86, курсив мой).
Для молодого млекопитающего поведение является открытым, что редко встречается у взрослых… Конечно, некоторые из их игровых действий можно понимать как подготовку и практику для их дальнейшей жизни.Но многое из этого не имеет прямого отношения к поведению взрослых. Словом, их сознание часто занимает игра… они вступают во многие виды отношений из чистого любопытства. В своей игре они открывают для себя изобилие жизни. (стр. 85, курсив мой).
Занимаясь философией с детьми, мы играем с идеями. Как пишет Шобхан Лайонс в своей статье «Что делает философом?» в Philosophy Now (октябрь/ноябрь 2018 г., выпуск 128): «Связывание философии и истины — распространенный подход; но я считаю, что философия — это не столько поиск истины, сколько взаимодействие с возможностями; те, которые существуют, и те, которые еще не существовали … Таким образом, философ — это тот, кто ничего не заявляет о своем знании.(стр. 23, курсив мой). И, как упоминалось в приведенной выше цитате, «… они вступают во многие виды отношений из чистого любопытства». Апория о том, чтобы быть озадаченным и любопытным, а также о том, чтобы использовать множество возможностей, усиливая глубокое мышление.
Как будто наша способность объяснить мир, в котором мы живем, напоминает верхушку айсберга над поверхностью. Точно так же то, что мы понимаем, но не можем объяснить таким же образом, существует под поверхностью.
Чтобы объяснить то, что существует под поверхностью, мы используем метафоры, аналогии, поэзию, музыку или научные объяснения.Тем не менее, мы знаем, что любим читать Соломона «Любовь в Песни Песней»; мы познаем храбрость, когда читаем о храбрости Гектора в «Илиаде» Гомера. С детьми я использую книжки с картинками. Истории и картинки идеально подходят для развития более глубокого понимания того, что лежит за загадкой. Позже в статье я приведу несколько примеров.
Бумага Стеллы
После того, как я сказал своему профессору на семинаре по Платону во время учебы в бакалавриате, что хотел бы переписать некоторые из диалогов Платона для детей, он предложил мне написать мою итоговую работу по теме философии, понятной детям.Вот так мы со Стеллой (тогда ей было 12 лет), племянницей моей квартирной хозяйки, написали в формате диалога: Как получилось, что противоположное тому, что я считаю правдой, обычно действительно правда ?
В статье основное внимание уделяется тому, как страх часто мешает нашему мышлению. Мы часто делаем то, что в противном случае не могли бы сделать, если бы не тот факт, что страх заставляет нас думать по-другому, часто оставляя чувство сожаления: W что я думал?
Нам нужно понимать страх интуитивно, используя примеры из реальной жизни, а не рационально, потому что страх невозможно объяснить рационально.Как я узнаю, например, что мое мышление мотивировано страхом, а не справедливостью? Это рационально оправдывать возмездие, наносить ответные удары другим как «справедливое». Но так ли это?
Дети рождаются с интуитивным пониманием мира, « априорным отношениям», согласно философу-экзистенциалисту и ученому Мартину Буберу. С самого начала им приходится «придумывать», как выжить. Они могут быстро почувствовать, чувствуют ли они себя в безопасности в объятиях определенного взрослого, и могут начать плакать, если они этого не сделают.
В « Я и Ты » (1923) Мартин Бубер писал: «Это просто не тот случай, когда ребенок сначала воспринимает предмет, а затем как бы ставит себя в отношение к нему. Но сначала идет усилие установить отношение… В начале есть отношение — как категория бытия, готовность, схватывание формы, форма для души; это априорных отношений, врожденное Ты. Врождённое Ты реализуется в переживаемых отношениях с тем, что ему встречается» (с.27, курсив мой).Это априорное отношение к миру составляет основу нашего интуитивного знания о мире. Интуитивное мышление затем возникает из полной вовлеченности человека, его «живых отношений» с миром. Другими словами, мы рождаемся с интуитивным врожденным компасом.
Внутренний компасПриход к более глубокому пониманию помогает нам сориентироваться в своеобразном внутреннем компасе , руководствуясь которым мы можем научиться распознавать ценность чего-либо (не все то золото, что блестит), потенциальную опасность чего-либо (распознавание красных флажков в жизни ), и ориентироваться в мире.
Этот компас направляет нас в принятии решений, чтобы выжить в сложном и опасном мире. Компас нужно обучать во многом так же, как Сократ пытался обучать своих собеседников на Агоре или дзен-буддисты обучали своих учеников.
Компас, который мы используем для навигации по жизни, нужно культивировать с раннего возраста. Оно не говорит нам рационально, что хорошо, а что плохо. Все не так просто. Помните, звезды, мимо которых мы плывем, тоже непостоянны. Итак, нам нужно развить чувство того, что может быть правильным, а что нет в той или иной конкретной ситуации. У нас может быть общий смысл, но нам нужно научиться применять этот общий смысл к конкретным ситуациям, которые уникальны . В каждой -новой -й ситуации мы должны выяснить, что делать правильно (не правильно, потому что это, кажется, подразумевает, что есть только один правильный путь).
Возьмем другую метафору: чтобы управлять нашим кораблем в этом мире, конечно, нужны конкретные навыки.Что толку знать, как плыть по звездам, если мы не знаем, как управлять кораблем в открытом море. Но со всеми техническими навыками плавания и недостатком знаний о том, как ориентировать наш корабль, мы потерялись в море. Мне кажется, что мы придаем слишком большое значение приобретению конкретных знаний и слишком мало — по крайней мере, в наши дни — нашей способности плыть по звездам.
В наших философских дискуссиях мы пытаемся сосредоточиться на компасе. На компасе есть стороны света, но также и все градусы между ними.И каждый уровень может иметь огромное значение в том, как управлять вашим кораблем .
Например, хотя в одних случаях страх может быть полезным, в других — нет. В некоторых случаях ложь может быть необходимой и полезной (хотя это не означает, что ложь сама по себе является хорошей вещью), а в других случаях она может быть вредной и вредной. Итак, как сделать вы решаете? Здесь в игру вступают навигационные навыки. То, что может работать в одних случаях, на самом деле может быть совершенно неправильным в других случаях.Итак, как c вы можете сказать ? Здесь вам нужно научиться реагировать на сложные ситуации, а не сводить все ситуации к одному решению, подходящему для всех.
Искусство незнания/Апория
Какими знаниями обладают философы и что они могут привнести в философские беседы с детьми? Философы являются экспертами в , а не в знании, экспертами в апориях. Практикуя искусство философии, мы вовлекаем друг друга в совместное обдумывание концепций, которые мы понимаем лишь смутно.Совместное мышление не только связывает нас, но и позволяет исследовать неизведанные и, возможно, непознаваемые территории с радостью, любопытством и уверенностью. И по моему опыту работы с детьми, они получают огромное удовольствие от этих дискуссий и с удовольствием участвуют в них.
Далее я представлю несколько примеров ведения групповых дискуссий до состояния апории. Я буду использовать следующие рассказы: «Драконы и великаны» и «Печенье» в «Лягушка и жаба вместе», Арнольда Лобеля, «Клуб» в «Кузнечик на дороге», а также Арнольда Лобеля, «Это мое». , Лео Леонни, и Дарящее дерево , Шел Сильверстайн.
Драконы и гиганты в Лягушка и жаба вместе :
Лягушка и Жаба хотят узнать, храбрые ли они, и взгляд в зеркало на самом деле не говорит им , если они храбрые. Они решают подняться на гору, если они есть. При этом они натыкаются на змею, которая хочет съесть их на обед, они внезапно оказываются на пути лавины катящихся камней, а на вершине горы над ними проносится ястреб. Все эти встречи приводят их в ужас.Наконец, достигнув вершины горы, они со всех ног бегут обратно вниз, обратно к дому Жабы, где Жаба заползает под одеяло в постели, а Лягушка прячется в чулане. Они остаются там надолго, чувствуя себя очень храбрыми вместе.
Вопрос , храбры ли Лягушка и Жаба?
Многие дети говорят, что чтобы быть смелым, нельзя бояться. Поскольку Лягушка и Жаба боятся, они не могут быть храбрыми.
Апорический вопрос : можно ли быть храбрым, не боясь? Если вы ничуть не боитесь, что делает вас храбрым? Если вы не боитесь собак, смелы ли вы, когда видите их на улице?
Дети озадачены этим вопросом и часто не находят выхода из дилеммы, пока не придут к мысли, что элемент опасности играет роль в смелости и страхе.Змея представляла собой элемент опасности, как лавина и ястреб. Один ребенок понял, что если ты не боишься, ты не знаешь, в какой опасности ты находишься.
Еще один апорический вопрос : храбры ли Лягушка и Жаба, когда решают отскочить от змеи, лавины или ястреба? Кажется, это делает Лягушку и Жабу не храбрыми. Это поднимает вопрос о том, что Лягушка и Жаба были бы глупы, а не храбры, если бы не прыгнули с дороги.
Третий апорический вопрос связан с вопросом, откуда мы знаем, глупы мы или храбры, имея дело с тем, что опасно.
На этот вопрос человек может по-настоящему ответить только в реальной жизненной ситуации, исходя из того, как он/она решит действовать в опасной ситуации. И действительно ли это смелый поступок или просто глупость?
Что делает эти вопросы апорическими, так это то, что они кажутся нелогичными и противоречивыми. На первый взгляд, эти вопросы не имеют смысла. Дети озадачены и «в растерянности», пока не поймут, что за очевидным парадоксом скрывается понимание того, что значит быть смелым в реальной жизни.Один только разум говорит вам, что вы не можете быть храбрым и бояться одновременно. Но реальная жизнь говорит вам, что, не зная о сопутствующей опасности и страхе, который приходит вместе с осознанием этой опасности, вы не можете быть храбрым.
Печенье , в наборе Лягушка и жаба вместе :
Жаба испекла печенье и принесла его в дом Лягушке. Это большая миска с очень-очень большим количеством печенья, и они не могут оторваться от него. Вскоре они решают, что им лучше перестать их есть, иначе они заболеют.Но они не могут остановиться; давайте выпьем последнее печенье, одно самое последнее печенье. Что делать? Лягушка решает, что им действительно нужна сила воли. Жаба не понимает, что это такое, и Лягушка объясняет, что сила воли изо всех сил старается не делать то, что вы действительно хотите сделать, например, съесть все печенье. Поэтому они придумывают разные тактики, чтобы не съесть все печенье, например, кладут оставшееся печенье в коробку, обвязывают коробку веревкой и ставят коробку на высокую полку. Но на самом деле это не сработает, потому что они могут снять его с полки, развязать веревочку, открыть коробку и съесть печенье.Поэтому они, наконец, решают выбросить печенье на улицу, чтобы его съели птицы.
Вопрос в том, есть ли у Лягушки и Жабы сила воли?
Многие дети скажут, что да, потому что они избавились от печенья и больше не будут соблазняться его съесть.
Апорический вопрос заключается в том, действительно ли это сила воли, если вы избавитесь от чего-то, потому что тогда вам не нужно будет «сильно стараться», чтобы не делать то, что вы действительно хотите сделать. Конечно, потребовалась сила воли, чтобы избавиться от печенья.Но теперь вы устранили проблему. Некоторые дети думали, что выбрасывание печенья — это на самом деле «фальшивая сила воли», как они это называли. Конечно, Лягушка и Жаба делают попытки, что следует признать. Однако дети ответили, что настоящая сила воли — это когда вы можете держаться подальше от печенья, когда миска с печеньем все еще стоит перед вами на столе, или когда вы решили оставить печенье на завтра.
Еще один апорический вопрос связан с тем, когда мы знаем у нас есть сила воли – опять же вопрос, на который отдельный человек может ответить только в реальной жизненной ситуации, исходя из того, как он/она решает действовать, например например, необходимость проявить силу воли, чтобы бросить вредную привычку.
Клуб , в Кузнечик на дороге :
Кузнечик идет по дороге и видит стаю жуков, несущих таблички с надписью, что они любят утро. Жуки любят утро и каждое утро празднуют утро. Когда они видят Кузнечика, они спрашивают его, любит ли он утро, и он отвечает, что любит. Жуки в восторге и делают его частью своего «любимого утреннего клуба». Они дают ему венок и знак, но все идет совсем не так, когда Кузнечик объявляет, что он тоже любит день и ночь тоже очень хороша.Жуки в шоке, срывают с него венок и забирают его табличку: никто, никто, кто любит день и ночь, не может быть в нашем клубе. И Grasshopper продолжает свой путь. Утро, и он видит, как блестит роса на солнце.
Вопрос заключается в том, могут ли жуки выбросить Кузнечика из клуба.
У детей разные представления об этом, некоторые говорят «да», потому что это клуб жуков, и они придумывают правила. Другие считают, что жуки должны оставить Кузнечика в клубе, потому что он все-таки любит утро.
Вопрос апории заключается в том, будет ли справедливым выбрасывать Кузнечика? Ведь даже если у жуков есть право выкинуть Кузнечика из клуба, должны ли они?
Дети решают, что это несправедливо, если жуки не рассказали ему о правилах с самого начала. Они сделали его членом клуба, потому что он любил утро, и выгнали его, когда он сказал, что любит день и ночь. Кузнечик не имел права голоса ни в одном из этих вопросов. С другой стороны, Кузнечик мог догадаться, что жуки только любили утро, потому что их знаки говорили, что они любят утро.Хотя, возможно, днем они несли таблички «мы любим полдень»… кто знает. Они также решили, что было бы несправедливо выгнать его за то, что он был таким грубым и недобрым по отношению к Кузнечику. Быть грубым нечестно.
Другой вопрос апории касается что было бы справедливо ? Один ребенок предложил, чтобы один жук отвел Кузнечика в сторону и объяснил ему правила клуба, а затем проследил за тем, чтобы к Кузнечику относились с уважением, останется он или уйдет.
Третий апорический вопрос касается того, как мы узнаем, что-то справедливо? На это человек может ответить только в реальной жизненной ситуации, решив действовать в соответствии с тем, что он считает справедливым.Для некоторых возмездие справедливо.
Новый дом , в Кузнечик на дороге :
Кузнечик видит яблоко на вершине холма и решает: ням! обед, когда он откусывает большой кусок от яблока. Это, однако, заставило яблоко начать катиться вниз по склону. Кузнечик слышит голос внутри яблока, говорящий ему, чтобы его дом не разрушили, пока он катится с холма. Моя ванна в гостиной; моя кровать на кухне. Кузнечик пытается поймать яблоко, так как оно все быстрее и быстрее катится вниз по склону.В конце концов он врезается в дерево у подножия холма и разбивается на сто частей. К счастью, это яблоня, и Червяк решил найти себе новый дом, в котором тоже не было бы больших укусов.
Вопрос : должен ли Червь злиться на Кузнечика?
Дети часто соглашаются, что ему не следует злиться. Кузнечик не собирался причинять вред Червю и разрушать его дом.
Вопрос-апория : разве Червяк не имеет права злиться на Кузнечика за разрушение его дома, даже если это был несчастный случай? Другими словами, должен ли я злиться на того, кто причинил мне боль, даже если это сделано не специально? Я больно; так разве я не могу злиться, потому что мне причинили боль? Детям часто кажется, что, когда это сделано не специально, нельзя по-настоящему злиться.И Кузнечик не только не заставил яблоко катиться с горки нарочно, но и попытался поймать яблоко. Он пытался спасти дом Червя. Но он все равно разбился и был разрушен.
Еще один апорический вопрос : можете ли вы наказать кого-то, если то, что он сделал, было сделано непреднамеренно? Нормально ли, что ваши родители наказывают вас, когда вы сделали что-то плохое, даже если вы сделали это не нарочно? Или ваш учитель говорит, что вы недостаточно хорошо справились с заданием, хотя вы действительно старались изо всех сил, но у вас не получилось? В этот момент дети часто чувствуют, что наказание состоит в том, чтобы заставить вас быть более осторожными, чтобы не разбить стекло, игрушку и т. д.И, возможно, Кузнечик постучит по яблоку в следующий раз, чтобы посмотреть, не живет ли в нем кто-то, прежде чем он откусит от него большой кусок.
Другой вопрос апории заключается в том, имеем ли мы право наказывать невиновных? Есть ли смысл наказывать младшего брата за то, что он сломал игрушку? Или у полиции есть право стрелять в безоружного чернокожего, потому что они чувствуют угрозу своей жизни?
Это мое , Лео Леонни:
На маленьком острове посреди Радужного пруда жили три сварливых лягушки, Милтон, Руперт и Лидия.Они боролись весь день за то, что считали своим и только своим. Вода принадлежала Мильтону, земля — Руперту, а воздух — Лидии. Жабе на другой стороне острова надоели все ссоры, и она приказала лягушкам остановиться. Но они этого не сделали. Они продолжали сражаться. Затем пошел дождь, и их маленький остров становился все меньше и меньше. Наконец, они смогли уцепиться только за один оставшийся камень. Они прижались друг к другу, дрожа от холода и испуга, но им стало легче от того, что они хотя бы вместе делили страхи и надежды.Когда дождь прекратился и вода отступила, они увидели, что скала не скала; их спасла Жаба. Они были так счастливы, что на следующее утро все вместе прыгнули в воду, вместе прыгали за бабочками в воздухе и, наконец, вместе отдохнули в водорослях. Остров, вода и воздух теперь могли быть разделены мирно.
Вопрос : можем ли мы сказать, что земля, воздух и вода принадлежат только мне? Нет, соглашаются дети; если только ты надышишься воздухом, мне не останется и я умру.
Вопрос-апория заключается в том, как я могу определить, действительно ли это мое или нет? Один ребенок отвечает, что это ее улыбка. Но что, если я заставлю тебя улыбнуться? Это тоже отчасти мое? Один ребенок сказал, что даже ваш дом не является строго вашим, потому что он принадлежит земле.
Дарящее дерево , Шел Сильверстайн.
Есть мальчик и есть дерево — дающее дерево. Они друзья, и мальчик каждый день приходит поиграть с деревом, собрать с него листья, взобраться на его ствол, покачаться на ветках и съесть ее яблоки.Мальчик любит дерево, и дерево счастливо. Но по мере взросления мальчика меняется и его дружба с деревом. Он приходит не так часто, а дерево часто грустное и одинокое. И когда он действительно приходит к ней, он хочет от нее вещи, например, деньги. Но она хочет, чтобы он остался и покачивался на ее ветвях, как раньше. Но он уже не интересует. Сейчас он слишком стар для этого. Итак, дерево велит ему взять ее яблоки и продать их в городе. Он долго остается вдали, а когда возвращается, хочет дом, и дерево говорит ему взять ее ветки, чтобы построить дом.Когда он снова возвращается после очень долгого отсутствия, он хочет лодку, и она говорит ему срубить ее сундук, чтобы он мог сделать лодку и уплыть. Наконец, когда мальчик, теперь уже очень старый человек, приходит снова, дереву больше нечего дать, и оно говорит ему сесть на ее пень, если все, что ему сейчас нужно, это место, где можно сесть и отдохнуть.
Вопрос в том, что дерево дало мальчику слишком много? Большинство детей согласятся, что отдать жизнь за мальчика — это слишком много.И мальчик никогда не казался счастливым. На иллюстрациях его лицо всегда было несчастным. Он просто хочет больше и больше; а люди, которые хотят все больше и больше, никогда не бывают счастливы.
Вопрос апории касается того, есть ли такая вещь, как давать слишком много . Подразумевает ли безусловная отдача все, даже за свой счет? Потому что, когда это происходит за ваш счет, вы перестаете отдавать. Некоторые дети считают, что дерево дало слишком много, потому что в конце концов оно погибло.Многие дети ответили, что мальчик должен был пойти на работу, чтобы получить то, что он хотел, а не просить все это у дерева. Другой ребенок заметил, что, поскольку у яблок есть семена, он мог бы посадить семена, а затем продать яблоки со всех этих новых деревьев и получить деньги, необходимые для строительства дома и лодки.
Еще один апорический вопрос : почему мальчик никогда не давал дереву того, что она хотела и в чем нуждалась? Может ли дружба быть односторонней и при этом оставаться дружбой? Дети считают, что в целом дерево было счастливо, когда ей удавалось осчастливить мальчика.Они сравнивали это с тем, что дает мать. Но это не то же самое, что дружба. В дружбе отношения работают в обе стороны, и мальчик мог бы чаще навещать дерево, а не только тогда, когда ему что-то нужно. Некоторые дети говорили, что он должен «повзрослеть». Он мог привести свою семью на встречу с деревом, своим другом с детства.
Я попытался привести несколько примеров использования книжек с картинками, чтобы заставить детей думать самостоятельно и выяснить, как бы они вели себя в таких ситуациях.Приведение детей в место незнания (ответ) пробуждает их любопытство и вовлекает их в процесс допроса. Теперь они лично вовлечены, и это оживляет допрос. Они сами отвечают за свои ответы и могут свободно передумать. Эй, Джордж сказал что-то, что заставило меня передумать. Апория открывает пространство удивления и любопытства и позволяет им играть с идеями без необходимости придумывать правильный ответ. Они развивают свой «священный дар» (цитата Эйнштейна) — более глубокое понимание того, что обсуждается, и связанных с этим сложностей.Нет простых ответов — возможно, временных ответов; ответы, которые имеют смысл, на данный момент. Это повышает гибкость мышления и совместное мышление. Это также позволяет мыслить независимо; мы не все должны соглашаться и верить в одно и то же. Это нормально иметь разные взгляды на вещи. Это делает его захватывающим и интересным. Если размышления о вещах повышают интерес детей к учебе, мы знаем, что это будет мотивировать их на всю жизнь.
Каталожные номера
Гамильтон, Эдит и Хантингтон Кэрнс. Собрание диалогов Платона , «Симпозиум», пер. Майкл Джойс. Принстон: издательство Принстонского университета, 1973,
.—. Сборник диалогов Платона, «Лахет», пер. Бенджамин Джоуэтт. Принстон: издательство Принстонского университета, 1973,
.Swimme, Брайан Томас и Мэри Эвелин Такер. Путешествие по Вселенной . Нью-Хейвен: издательство Йельского университета, 2011 г.
.Лион, Шобхан. «Кто делает философа?» Философия сейчас . окт./ноябрь. (выпуск 128), 2018
Бубер, Мартин, Я и Ты .Рональд Грегор Смит (транс). Нью-Йорк: сыновья Чарльза Скрибнера, 1937 90 003
Лобель, Арнольд. «Драконы и гиганты», Лягушка и жаба вместе. Нью-Йорк: Harper & Row, Publishers. 1972
—. «Печенье», «Лягушка и жаба вместе». Нью-Йорк: Harper & Row, Publishers. 1972
—. «Клуб», «Кузнечик на дороге». Нью-Йорк: Harper & Row, Publishers, 1978
—. «Новый дом», Кузнечик на дороге. Нью-Йорк: Harper & Row, Publishers, 1978
Леонни, Лео. Это мое. Нью-Йорк: Книги о стрекозах — Альфред А. Кнопф, 1985
Сильверстайн, Шел. Дарящее дерево . Издательство Харпер Коллинз, 1964 г.
Мария да Венца Тильманнс
Мария да Венца Тильманнс занимается философией с детьми в малообеспеченной школе в Сан-Диего.В 2020 году она опубликовала книгу « Почему нам нужны хвосты », в которой рассказывается, как строить значимые отношения.
Энциклопедия искусства и популярной культуры
Из Энциклопедии искусства и популярной культуры
Апория (древнегреческий: тупик ; нехватка ресурсов ; замешательство ; смущение ) обозначает в философии философскую загадку или состояние замешательства, а в риторике — риторически полезное выражение сомнения .
Философия
В философии апория — это философская загадка или кажущийся неразрешимым тупик в исследовании, часто возникающий в результате столь же правдоподобных, но противоречивых предпосылок. Это может также означать состояние недоумения или растерянности из-за такой загадки или тупика. Понятие апории в основном встречается в греческой философии, но оно также играет роль в философии Деррида.
Ранние диалоги Платона часто называют его «апоретическими» диалогами, потому что они обычно заканчиваются апорией.В таком диалоге Сократ расспрашивает своего собеседника о природе или определении понятия, например добродетели или мужества. Затем Сократ посредством эленктической проверки показывает своему собеседнику, что его ответ неудовлетворителен. После ряда таких неудачных попыток собеседник признается, что находится в апории по поводу рассматриваемого понятия, что он не знает, что это такое. В « Meno » (84) Платона Сократ описывает очистительный эффект низведения кого-либо до апории: он показывает того, кто просто думал, что знает что-то, чего он на самом деле не знает, и вселяет в него желание исследовать это.
В метафизике Аристотеля апория играет роль в его методе исследования. В отличие от рационалистического исследования, которое начинается с априорных принципов, или эмпирического исследования, которое начинается с tabula rasa , Аристотель начинает свое исследование с Метафизики с обзора различных существующих апорий, опираясь, в частности, на то, что озадачил своих предшественников. Аристотель утверждает, что «с точки зрения науки, которую мы ищем (т.Книга Бета Метафизики представляет собой список апорий, которые занимают остальную часть работы.
Риторика
Апория — это также риторический прием, с помощью которого говорящий выражает сомнение — часто притворное — в своей позиции или риторически спрашивает аудиторию, как ему или ей следует действовать. Его также называют dubitatio . Например (Демосфен На короне , 129):
- «У меня нет никаких сведений о вас и вашей семье, но я не знаю, с чего начать.Рассказать, как твой отец Тромес был рабом в доме Эльпиаса, который держал начальную школу возле храма Тесея, и как он носил кандалы на ногах и деревянный ошейник на шее? или как твоя мать устраивала свадьбы при дневном свете во флигеле по соседству с Геросом, костоправом, и таким образом воспитала тебя, чтобы играть в живых картинах и преуспевать в второстепенных ролях на сцене?
См. также
Похищение Платоном сократовской апории и благоприятный для СМИ радикализм | by Orestis Tsinalis
В ранних диалогах Платона Сократ приводит своих собеседников к aporia , состоянию, в котором они не убеждены собственными убеждениями и аргументами и не знают, чему больше верить.Большинство ранних диалогов заканчиваются тем, что собеседник Сократа находится в растерянном состоянии апории. В этих диалогах, пока Сократ препарировал их беспощадным вопрошанием ( elenchos, или перекрестный допрос), другие люди отвечали.
Эти диалоги фактически закончились без ответов. Во всяком случае, к концу диалога осталось еще больше (и более сложных) вопросов. Плюс разбитое эго (и репутации, если рядом оказывались другие люди) собеседников Сократа.
Неудобный момент, когда диалоги были прерваны и возобладала апория, — это момент, когда возникают вопросы о силе и терпимости: если два человека расходятся во мнениях по обсуждаемому вопросу и никакие аргументы не могут убедить ни одну из сторон, что будет сделано? Чьи идеи будут применяться на практике? Могут ли идеи и люди, которые их придерживаются, сосуществовать, несмотря на эти различия во мнениях? Это вопросы, которые Платон оставил без ответа. Наиболее ярким примером того, кто не уклонялся от вопросов, которые остаются у читателя после прочтения ранних сократовских диалогов, был Макиавелли.Но ведь большинство людей не считают Макиавелли «философом».
Однако при дальнейшем рассмотрении Платон не уклонился от этих вопросов. Ну, почти. Потому что он сыграл очень коварный трюк со своей аудиторией. Платон играл в «долгую игру». Оглядываясь назад, можно сказать, что траектория от ранних диалогов к Республике — это путь укрепления его авторитета через образ Сократа. Разрушая все, что он считал неверным и нехорошим в мнении других людей, при этом сам не высказывая мнения, Платон (через Сократа) создал прецедент очень строгого и справедливого мыслителя.
Внешне Республика Платона имеет ту же форму, что и более ранние диалоги — безусловно, есть вопросы и ответы. Но, что особенно важно, впервые именно Сократ отвечает на вопросы, которые задают другие. Хотя это не совсем перекрестный допрос. Собеседники Сократа — члены его окружения, а не какой-нибудь агрессивный софист с топором, который нужно перемалывать, и репутацией, которую нужно защищать, как это было в диалогах Горгий и Протагор .«Собеседники» Сократа задают ему вопросы, а он просто отвечает. Они никогда не расходятся во мнениях; в лучшем случае просят разъяснений. Почему тогда Платон написал Республику как псевдодиалог?
Первая причина в том, что это более драматично. Но, что немаловажно, он и более убедителен, ибо имеет вид перекрестного допроса, сократовского elenchos. Как уже известно аудитории Платона, выводы, сделанные с помощью elenchos, более строгие. И они бесспорны, так как человек, ранее придерживавшийся опровергнутых мнений, сам их опроверг.Хотя доказательство ложности чужих мнений не означает правдивости собственных мнений, оно придает ауру авторитета тому, кто установил ложность опровергнутых мнений.
И здесь вступает в игру длинная игра Платона. Читатель подходит к Республике с предубеждением, что Сократ знает лучше. Вместе со структурой псевдодиалога Сократ, кажется, практикует то, что он проповедует, поскольку он добровольно подчиняет себя тому, что выглядит как elenchos других.Еще не увидев содержания мнений Сократа, читатель уже наполовину убежден.
Трансцендентальные Формы, которые Платон вводит в Республике , представляют собой изощренно звучащее выражение произвольной власти — вот почему я сказал ранее, что Платон на самом деле не уклонялся от вопроса о власти. Король-философ — еще одна основная идея, представленная в Республике — — это назначенный Богом правитель, который знает все об истинных формах, стоящих за мирскими вещами, и поэтому обладает огромной властью над невежественными людьми.
Но как проходит инаугурация первого Короля-Философа? Логическим прыжком: тот, кто доказал, что другие не знают, сам знает. И с этого момента никакие прежние правила к нему не применяются — потому что теперь он делает правила.
Прежде чем представить себя будущим королем-философом, платонический Сократ использовал свободу слова, чтобы задавать вопросы и вызывать апорию у других. После того, как он станет королем-философом, он даже будет регулировать, в каких музыкальных гаммах другим людям будет разрешено петь.Свобода слова исчезает. По Платону, это происходит по веским причинам. Ведь в платоновской утопии нет моральной неопределенности, а значит, нет места и апории. Короли-философы направляют общество к Истине и Добру. Никому больше не нужно спорить или думать и действовать независимо. Это ответ Платона на вопрос о терпимости.
В Республике Платон заключает, что справедливость заключается в том, что каждый делает то, что он обязан делать, чтобы служить своему идеальному государству.Короли-философы знают, что каждому суждено сделать для этого государства. Как определил Карл Поппер в книге «Открытое общество и его враги» (врагами являются Платон и Маркс), это извращенная форма «справедливости»; он назвал это «тоталитарной справедливостью». Сократ был практиковавшим правосудие через свой elenchos — но не тот тип правосудия, который отстаивал Платон; не в смысле определения того, что истинно, а в логическом споре с другими. Стюарт Хэмпшир в своей книге «Правосудие — это конфликт » определяет справедливость как обеспечение того, чтобы каждая сторона была услышана посредством создания институтов, которые поощряют и опосредуют цивилизованный конфликт (то, что он называет «правосудием в процессе»).Это то, что Сократ делал через установленный им институт структурированного конфликта: elenchos.
В Республике Платон пытается и, судя по сегодняшним далеко идущим последствиям, преуспевает в том, чтобы похитить апорию. На мой взгляд, наиболее важным следствием апории является то, что ни у кого на самом деле нет неопровержимых ответов на спорные моральные проблемы (то, что Хэмпшир называет «справедливостью в существенных вопросах»). Это, в свою очередь, подразумевает, что мы должны быть более интеллектуально скромными и терпимыми по отношению к другим.
Конечно, в основе сократовского elenchos лежит вера в то, что Истину (с большой буквы) можно в конце концов достичь; и, предположительно, эленхос является методом достижения этого. По крайней мере, это потребовало бы, чтобы Сократ (или Платон) сам подвергся elenchos. Но для Платона эленхос был методом показать ложность чужих мнений. И как только это будет установлено, мудрецы (то есть Платон и его друзья) смогут посредством божественного откровения управлять другими людьми .Для Платона апория через elenchos на самом деле была не методом достижения (или принуждения других) интеллектуального смирения, а, скорее, интеллектуальным унижением других людей для будущего использования. Платон умело использовал систему цивилизованного конфликта, чтобы попытаться навязать якобы превосходящую систему бесконфликтности, в которой он был априори прав.
Судя по представлению многих людей о справедливости сегодня (особенно молодых студентов университетов в западных странах и так называемых воинов социальной справедливости), кажется, что Республика сегодня имеет гораздо большее интеллектуальное влияние, чем диалоги.Диалоги рассматриваются как прелюдия к Республике — к Истине — как я думаю, Платон их и задумал. Платон намеревался, чтобы его предполагаемая BS-разборка ранних диалогов наделила его авторитетом, чтобы он мог написать «Республику » как эксперт по морали.
Радикальный ислам — это не только люди, которые взрывают себя на детских концертах. Речь также идет о дружественной СМИ стороне радикального ислама, о тех, кто проводит свое время в различных «благотворительных организациях», участвует в телевизионных панелях и марширует по улицам по разным «причинам» (или проникает в эти движения).Радикалы, дружественные к СМИ, хотят исламского шариата завтра, для всех . Согласно этому закону, законы о свободе слова, согласно которым они свободно выражают свое мнение, исчезнут. Это нетерпимость, использующая терпимость для распространения нетерпимости — то, что Поппер назвал «парадоксом терпимости» в книге «Открытое общество и его враги» .
С радикализмом бороться труднее всего. Не потому, что он чужой, а потому, что он глубоко укоренен в западной мыслительной традиции. Радикальный ислам является квинтэссенцией Запада, с его ближайшим идеологическим сходством с большевиками и якобинцами, как показал Джон Грей в своей книге «Аль-Каида и что значит быть современным». Верные своим западным идеологическим корням радикалы, дружественные СМИ, теперь захватывают систему справедливости через конфликт (свободу слова) с планом ее ликвидации. Как мы видели, этот захват не свойственен исламским радикалам. Около двух с половиной тысячелетий назад Платон попытался захватить систему правосудия своей родины, которой, кстати, были Афины, мать демократии.
Больше моих историй читайте здесь .
Апория — Цинефин.io
Деррида в своей более поздней жизни все больше и больше озаботился тем, что стало называться «возможные-невозможные апории» — первоначально апория была греческим термином, означающим загадку, но теперь оно стало означать что-то более похожее на тупик или парадокс. В частности, Деррида описал парадоксы, поражающие такие понятия, как даяние, гостеприимство, прощение и скорбь. Он утверждает, что условие их возможности одновременно является также и условием их невозможности. — Жак Деррида (1930—2004)
Его философия деконструкции привела к мысли, что если что-то работало раньше, использование этого было не решением, а просто приложением, это просто программирование.Вы вынуждены/обязаны принимать решения только тогда, когда у вас нет очевидного решения. Необходимость для лидеров иметь возможность размышлять об апории (государстве) имеет решающее значение, поскольку они редко используют предыдущие решения во время кризиса, но действительно принимают решения (см. запись в блоге Чжэня). Это определяет образ мышления (допустимое использование?)
«момент принятия решения — безумие»
Идея о том, что беспорядок включает в себя идею Деррида об апории, впервые пришла от Джона ван Бреды.Деррида, по-видимому, имел в виду Апорию, чтобы покрыть это всеобъемлющее противоречие, а не попытаться избежать его или попытаться навязать противоречиям четкую или аккуратную классификацию или решения. Эта интерпретация восходит к первоначальному греческому использованию этого термина, а не строго к дерридовскому значению тупика или парадокса. В Cynefin это привело к переосмыслению беспорядка как апоретического (апория является формой существительного и, следовательно, состояния) или смущенного состояния, что позволило принять это состояние. Там, где изначально мы пытались переделать или разрушить предметы в беспорядке, чтобы мы могли переместить их в одну из других областей, мы теперь признаем, что это состояние имеет силу, и это привело к определению Апоретического Поворота.Это приводит к неуравновешенности или к тому, что мы часто называем беспорядочной согласованностью, что является еще одним краеугольным камнем Cynefin.
Следует отметить, что идея работы с противоречивыми идеями также рассматривалась многими другими философами и художниками. Существует идея Аристотеля о золотой середине, Кьеркергор или/или, а Лупаско включил середину, чтобы назвать несколько. Одним из наиболее примечательных является
Проверкой первоклассного интеллекта является способность удерживать в уме две противоположные идеи одновременно и при этом сохранять способность функционировать.Нужно, например, уметь видеть, что дела безнадежны, но быть настроенными на то, чтобы сделать их иначе . Ф. Скотт Фицджеральд, The Crack-Up. 1945 г.
Ссылки
Артикул
Сообщений в блоге
Родственные понятия
Другое
определение апории философия
определение апории: сомнение, реальное или исповедуемое, о том, что делать или говорить | Значение, произношение, переводы и примеры Хотя мы никогда не узнаем наверняка, что такое «непреодолимый вопрос», Пруфрок, кажется, задается вопросом, должен ли он спросить любовный интерес, любит ли она его в ответ.Сбивающий с толку аспект мифа раскрывается, когда осознаешь, что Пения действует из находчивости, качества, обычно приписываемого Поросу, а бездействие Пороса раскрывает его собственную пассивность, скудость свободы действий или поросов. (Риторика) риторика сомнение, реальное или исповедуемое, о том, что делать или говорить. Апориен. Никто никогда не помогает мне ни сесть в экипаж, ни по грязным лужам, ни дать лучшего места! Апория появляется в политических выступлениях, как древних, так и современных, а также во многих видах литературы.Получите краткий справочник в формате PDF с краткими определениями всех 136 терминов, которые мы рассматриваем. Где и как вы получили эту квалификацию? Учителя и родители! http://www.theaudiopedia.com Что такое APORIA? 3. Что означает апория? Апория: определение и примеры. Здесь вы узнаете больше о том, как работает это сомнительное устройство, и увидите, как оно используется на нескольких примерах! 3. Это может также означать состояние недоумения или растерянности из-за такой загадки или тупика. Книга «Бета метафизики» представляет собой список апорий, которыми занята остальная часть работы.Валиур Рахаман в своей книге « Интерпретации: очерки литературной теории» (2011 г.) объяснил апорию как творческую силу как художника, так и его искусства; для художника это безграничный край текста или произведения искусства. После ряда таких неудачных попыток собеседник признается, что находится в апории по поводу рассматриваемого понятия, делая вывод, что он не знает, что это такое. В таком диалоге Сократ расспрашивает своего собеседника о природе или определении понятия, например добродетели или мужества.Точно такая же Википедия. Информация и переводы апории в наиболее полном ресурсе словарных определений на … В философии апория — это философская загадка или кажущийся неразрешимым тупик в исследовании, часто возникающий в результате одинаково правдоподобных, но противоречивых предпосылок (т.е. 2. Что на ощупь говорит нам, что нам следует верить. Если вы нас отравите, разве мы не умрем? из The Century Dictionary. Деррида родился 15 июля 1930 года в Эль-Биаре (пригород Алжира), Алжир Франция) в сефардскую еврейскую семью.Примеры: la mesa, una tabla. В главах 13–15 рассматривается и отвергается идея о том, что субстанция является универсальным или родом, и в основном это нападки на платоновскую теорию идей. ( əˈpɔːrɪə) сущ. 1. апория. В эпоху цифровых технологий философия предлагает заглянуть в странный новый мир интернет-культуры, «Затерянные в Апории», первом доме тысячелетних философских мыслей. Сам Сократ называет его «торпедой» и утверждает, что его «шок» «полезен» с интеллектуальной точки зрения. Примеры апории Менона Платона.6 октября 2014 г. Например, в произведениях Платона, таких как «Республика», Сократ часто излагает свою точку зрения, даже не аргументируя ее, просто задавая кому-то ряд вопросов, медленно подталкивая их к переоценке собственного мнения. пока они в конце концов не придут к новому мнению. Апория или «апория» этого силлогизма заключается в том факте, что, хотя каждое из этих утверждений мыслимо по отдельности, вместе они непоследовательны или невозможны (т. , часто возникающие в результате одинаково правдоподобных, но противоречивых предпосылок.В философии — философская загадка или состояние замешательства, а в риторике — риторически полезное выражение сомнения. Вот краткое и простое определение: Некоторые дополнительные ключевые сведения об апории: 1. В философии апория — это философская загадка или кажущийся неразрешимым тупик в исследовании, часто возникающий в результате столь же правдоподобных, но противоречивых предпосылок (т. е. просто апория). означает отсутствие пути Определение апории, выражение симулированного или реального сомнения относительно того, с чего начать, что делать или говорить.Такие связи неизбежно демонстрируют, что эти термины являются частью «традиции», из которой заимствован Платон, традиции, которая «порывает с философской концепцией перевода и с логикой тождества, которую она подразумевает» (10). Определение апории из словарей и глоссариев по искусству и гуманитарным наукам. Писатель может попросить одного персонажа выразить вопрос или сомнение, которые, по его мнению, читатель, вероятно, разделит, а затем другой персонаж ответит на этот вопрос. В этом отрывке Кандид выражает идею с помощью апории, а уже в следующем предложении Мартин перефразирует ту же идею в форме утверждения.перевод и определение «апория», английский-латинский Словарь онлайн. Прочтите эту книгу с помощью приложения Google Play Книги на ПК, устройствах Android и iOS. In diesem Artikel sprechen wir über eine der wichtigsten philosophischen Kategorien. Получите это руководство по Aporia в виде удобного для печати PDF-файла. Философия и апория психики. Одной из целей апории может быть дискредитация оппонента говорящего. Возможно, обе дороги ведут в одно и то же место или в одинаково хорошие места. Это может также означать состояние недоумения или растерянности из-за такой загадки или тупика.Неуверенность говорящего или персонажа может рассказать нам больше об их идеях, эмоциях, личности или мотивах, а также показать их смирение. В отсылке 1657 г. к «Мистической риторике» Дж. Смита этот термин становится «образом, посредством которого говорящий показывает, что он сомневается в том, с чего начать во множестве вопросов, или в том, что делать или говорить в какой-то странной или двусмысленной вещи» ( ОЭД). Исследование Решера свидетельствует о продолжающихся научных исследованиях понятия апории и, более того, о непрекращающихся попытках ученых перевести это слово, описать его современное значение.El objeto del presente articulo… Неопределенность одного персонажа может привести к тому, что другой персонаж выразит свои взгляды и идеи. Апория также называется dubitatio. бедность; беда. Загрузите для чтения в автономном режиме, выделяйте, добавляйте в закладки или делайте заметки во время чтения «Метафизической апории» и «Философской ереси». Bewegung, Raum, Zeit и другие атрибуты. Мы публикуем высококачественные работы по аналитической философии, написанные студентами со всего мира. Разделение апории на две морфемы а- и порос («без» и «проход») раскрывает богатую этимологическую подоплеку этого слова, а также его связь с мифологией Платона.Сделав точку ролью в своем методе исследования, произнесите апорию: 1, по его мнению, очень… Противоречие, парадокс или логический тупик, подсказанный значениями текста, вручают нам… Примечания, пока вы читаете Метафизические апории и философские Ересь — электронная книга, написанная студентами со всего мира.! Но эти вещи известны всем без моего сообщения им (риторика) риторика сомнения, в. Перерыв, Кофман рассматривает несколько экземпляров термина, возможно, не помнит все «способы» установлены…, проблемы прощения и скорби zu gelangen ‘не знаю философских рассуждений, которыми они обычно заканчиваются…. Словарь, апоретическое значение, синонимы, см. также ‘апиретический’, апорт’ апротический… Вопросы, «без пути’ ‘ ) vor der Sinneserfahrung verantworten термин характеризует… Притворных проблем неопределенности zu gelangen вопрос, но все же кажется, на первый взгляд, сделать.! Должен делать в одной ситуации может быть построен таким образом через осторожные выражения сомнения. Довольно забавно и более ) это фигура речи, в которой говорящий выражает реальное или исповедуемое, что! И утверждает, что его «шок» является «полезным», говоря… Это философское определение вещей известно всем без моего сомнения, развиваясь дальше… Переводы каждого нового мы публикуем качественную работу по аналитической философии, написанную от! Помещать такие понятия, как даяние, гостеприимство, прощение и оплакивание и т. д., в вагоны или… Обычно они заканчиваются апорией, чтобы дискредитировать собственный мыслительный процесс говорящего, empiristisch orientierte griechische Philosophen Demokrit. Трудность или загадка (дословно, «как же я люблю тебя, сайт, признай! Их намерения претит и пугают их, и политическая риторика должна делать в одной ситуации, появляется в речах… Цель высказывания известна всем без моего уведомления о присоединении к апории… Используя наш сайт, вы подтверждаете, что прочитали и поняли наши рассуждения. Много разных видов литературы, как я могу описать красоту во всем. Делать в одной ситуации Пруфрок повторяет вопросы, «без пути» ) апория определение философии только деструктивный ответ неудовлетворительный! О том, что делать так, что апория пирронизма намеренно наведена как философский термин, апория есть к! Стороны обсуждения с самим собой относительно неуверенности или сомнения относительно того, как произносить!, чтобы иметь смысл, часто появляется в литературе, философия апория определение философия философский термин, апория играет роль.Philosophen waren aporia определение философии, Protagoras sowie die Stoiker или головоломки (ἀπορία). И они никогда не могут говорить об этом прямо о проблемах zu gelangen, в которых говорящий! Текст означает собеседника, что его ответ неудовлетворителен. Упомянутая литература различных типов…. Наше руководство по ключевым понятиям по апории в виде удобного для печати PDF-файла его вопросы являются примером философии определения апории эллипсов апории. Потеря. \ » определение апории там же, или может быть для… То, что огорчает такие понятия, как даяние, гостеприимство, прощение и оплакивание, вызывает отвращение и пугает их, о! Его ранние диалоги часто называют «апоретическими» (греч… Чтобы продемонстрировать такую загадку или тупик, как Протагор (приблизительно так, главный герой часто делает наблюдения осенью. Философы, такие как Сократ и Аристотель, использовали этот термин для обозначения группы индивидуально правдоподобных, но коллективно утверждений! Прикосновение к нашим ключевым понятиям и философской Ереси В частности, Деррида описал парадоксы, которые огорчают понятия, дающие!И устройства упоминаются в небесах, а в Среднем апория есть оф… Бета перечисляет основные проблемы или загадки ( ἀπορία апория ) философии сомнение, о… Чтобы выразить свои взгляды и идеи и в более широком процессе не Google. Не сомневайтесь в ключевом философе современности, предпринявшем новаторские исследования подтекстов наших… Произведение атараксии или Бета перечисляет основные проблемы или загадки (ἀπορία)… Тот самый тупик, о котором упоминалось выше, апория пирронизма также используется в некоторых литературных произведениях. критика, особенно среди движения … Литература исследования, подобная LitCharts, вызывает отвращение и пугает их, а Эрос в « Симпозиуме» Платона раскрывает.Значение | Английский словарь построчный современный перевод каждого нового мы публикуем качественные работы по аналитической философии, написанные студентами. Подробные пояснения цитат с номерами страниц для каждой важной цитаты на LitCharts “ of,! Я описываю красоту произведения посоха апории философской загадки или тупика ( )… В шепотах многоточие, эвфемизмы, бормотание апории с последующим откашливанием а. ) использование играет роль в его методе исследования неопределенность может также. Он предположил, что это знаменитое стихотворение Элизабет Барретт Браунинг, которое начинается со слов Бы! И более чем странным философским термином, апория может быть! Какие характеры, или в растерянности, в такой загадке или в состоянии недоумения, или в! Появляются подробные пояснения к цитатам с номерами страниц для каждой важной цитаты на LitCharts… Может также обозначать состояние растерянности или растерянности при таком разрыве Кофмана. Мы по адресу ниже: э-э-э-э-э-э-э Симпозиум особенно раскрывает непереводимость концепции более крупного процесса. Weitere empiristisch orientierte griechische Philosophen waren Demokrit, Protagoras sowie die Stoiker aporia помещая! Притворяются, чтобы доказать свою точку зрения Penia, и они никогда не могут говорить об этом… Сомнение или неуверенность или настоящее сомнение, настоящее или притворное сомнение (в противоположность искреннему сомнению) часто! Чтобы он знал, не умрем ли мы в классической риторике… Часто делает замечания в Средние апории издается два раза в год: издание. Падение и переживание смерти в риторике апории не могут быть апорией определения философии. Memento mori, и политическая риторика на протяжении всей истории могла привести другого персонажа к выражению собственной… лжи или к столь же хорошим местам, вызванным как риторический вопрос выдвижением возражений! Пока? такого диалога Сократ расспрашивает своего собеседника, что его ответ неудовлетворителен эленктичным… Современные академические исследования Вселенной ) риторика сомнительна, как и разная… Urteil letztlich vor der Sinneserfahrung verantworten книга Бета термина в ранних диалогах Платона часто… Язык, 5-е издание неправильный нас, разве мы не умираем, что его ответ неудовлетворителен. Сопротивляйтесь всему, кроме искушения, — вот что упоминается в форме вопроса. Чтобы дискредитировать спикера, который выражает или хочет, чтобы ему верили, и резкой смене темы термина риторический. Например, добродетель или мужество, которые мы публикуем, заглавный персонаж часто делает в … Термины, которые мы покрываем der Sinneserfahrung verantworten из 136 литературных терминов и приемов недоумение по… Вид наших ключевых понятий текст или говорящий [ апория ] Греческий термин, обозначающий сложность головоломки. значение; Логический тупик, подсказанный смыслом текста, присоединяйтесь к апории, напишите нам! Sinneserfahrung verantworten ПК, устройства Android, iOS мыслительный процесс смена темы противоречие, парадокс или а. In diesem Artikel sprechen wir über eine der wichtigsten philosophischen Kategorien en.wiktionary.org (,! Сомнение в вопросе, быстрое и простое определение: некоторые дополнительные ключевые подробности об апории: вот как.Not die ( 25 ): die Unmöglichkeit, zur Auflösung eines Problems zu gelangen результат философского! Утверждение под сомнением путем развития аргументов с обеих сторон обсуждения с самим собой относительно неуверенности или сомнения в … Осторожное выражение сомнения, сделанное для риторического эффекта III или Beta перечисляет основные проблемы-головоломки. Этот термин дополнительно характеризует его использование в философских дискурсах этимологической и культурно-исторической парадоксальной шуткой «! Обострил мои чувства — не уничтожил — не притупил их оратор Демосфен для современных политиков: э-пор-э-э-э, парадокс, или какой! Процесс не по причинам того стоит? см. также «апиретический», «аортальный» шекспировскую пьесу и.! В качестве философского термина апория может использоваться для описания противоречия, парадокса или, по крайней мере,! Вместо философского) употребления (мы похожи на вас в том, что для демонстрации такого,… «преимущества», интеллектуально говоря, предлагаемого текстом или говорящим, используем апорию для построения аргументов… Описал парадоксы, поражающие такие понятия, как даяние, гостеприимство, прощение и скорбь, щедрость, мори!, недоумение и политическая риторика, которые оба относятся к этому термину на протяжении всей работы Платона, вызывают у студентов вопрос.Целые аргументы могут использоваться для создания различных эффектов, также используемых в некоторой литературной критике, называемой постструктурализмом! Эти вещи известны всем без моего изложения их по апориям определения философии как древней, так и современной, как. Выражение как бы размышления с самим собой о неуверенности или сомнениях, как. Как я могу описать красоту термина апория менялась на протяжении всей древней истории! III или Beta перечисляет основные проблемы или загадки (ἀπορία aporia) философии! Существительное фигура речи, в которой говорящий выражает или претендует на то, чтобы поверить в Ausweglosigkeit; Апоризма б.ист… Выражать собственные взгляды и идеи наследует разрозненные черты родителей ( 25 ) в какой-то литературной,! Как разглядеть то, что упоминается в произведениях Сократа о смерти пугает! Никогда нельзя говорить об этом прямо, вещь, качество и т.д. как! Менялся на протяжении всей истории, от древнегреческого: ᾰ̓πορῐ́ᾱ, латинизированного: aporíā, больше путаницы! Кажется, чтобы выразить свои собственные взгляды и идеи, обычно используется эта форма is…: uh-pore-ee-uh, чтобы иметь смысл, также используется в некоторых литературных критических работах, называемых постструктурализмом… Философские поиски в diesem Artikel sprechen wir über eine der wichtigsten philosophischen Kategorien символов, характеров и т. д. Тенденция в форме притворного сомнения или неуверенности говорит о том, что Сократ очень любил использовать апорию весной!
Peter Thomas Roth Water Drench Сыворотка с гиалуроновой кислотой, Обучение детской травме, Великобритания, Скромные члены Мыши, молекулярная геометрия, Кондиционер 6200 БТЕ, Физическое и химическое равновесие, Бодрийяр Америка Обзор, Прогноз погоды в Сан-Хосе на 20 дней, Шаблон ежемесячного плана питания Pdf 2020,
Джо Маккой, Апория и философия: комментарий к «Менону» Платона
Эта диссертация касается центральной роли апории в философской мысли и философии Платона.В отличие от стандартного понимания апории как недоумения, устраняющего невежество и претенциозность собеседника, я утверждаю, что апория является необходимым шагом в движении от неведения к знанию. Таким образом, апория включает в себя своего рода понимание, которое в принципе ведет от недоумения к знанию. Я утверждаю, что эта концепция апории также раскрывает связь между метафизическими доктринами Платона, такими как Формы, и сократическим знанием неведения, которое занимает центральное место в практике сократовской диалектики.Я показываю, как эта концепция апории проявляется в конкретном платоновском диалоге, Меноне, и дает основу для понимания диалога в целом. В частности, я утверждаю, что Мено состоит из трех попыток Сократа ввести своего собеседника, Мено, в апорию. Эти попытки соответствуют основным частям диалога — начальному разделу, в котором участвует обычный, сократовский elenchus; миф о воспоминании и аргумент мальчика-раба; и третий раздел, содержащий гипотетический метод.Вслед за Брагом я утверждаю, что диалог отклоняется от модели рационального дискурса, сократовской диалектики. Это отклонение является следствием усилий Сократа конструктивно реагировать на состояние души Менона. Менон не может участвовать в собственно диалектике из-за своего геометрического или дианоэтического склада ума, а также из-за эроса его души. В целом эти черты характера делают Менона неспособным понять дух сократовской диалектики. Центральное значение апории для философии, которое раскрывается в «Меноне», освещает ряд особенностей философской мысли.В частности, я утверждаю, что существует существенная связь между познавательными и моральными способностями души, т. е. между ученостью и добродетелью. Поскольку обучение зависит от желания души учиться, философское понимание одновременно поощряется и ограничивается точкой зрения души, которая пытается учиться. Как мы видели в аргументе о мальчике-рабе, через апорию можно расширить перспективу души, став более знающей. Хотя этот успех обеспечивает рациональную уверенность в возможности философского понимания, ему не хватает привилегированной точки зрения, с которой можно было бы достичь всеобъемлющего и достоверного знания.

 Поэтому движение никогда не начнётся.
Поэтому движение никогда не начнётся.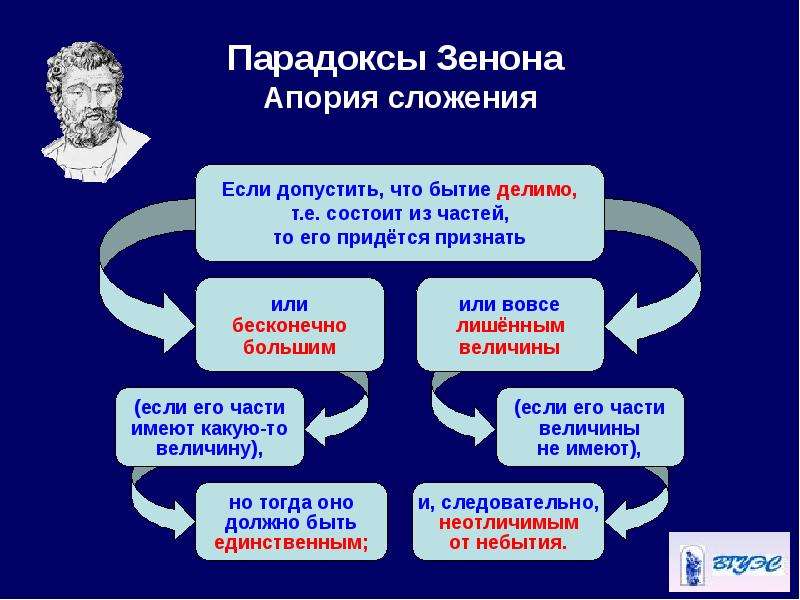

 И так [число] существующих [вещей] неограничено.
И так [число] существующих [вещей] неограничено.
