Психологика — Апории Зенона

Точные тексты апорий Зенона до нашего времени не дошли. Вместо них имеется более или менее подробный их пересказ в книге Аристотеля «Физика». Ниже приводятся все цитаты из этой книги, которые имеют отношение к апориям.

К тому же и с помощью обычных рассуждений легко уясняется, что величина непрерывна, если время непрерывно, поскольку в половинное время проходится половинный путь, и вообще в меньшее время — меньший, ибо одни и те же деления будут и для времени, и для величины. И если одно из них бесконечно, то будет [бесконечно] и другое, и в каком смысле [бесконечно] одно, в таком и другое, например, если время бесконечно в отношении концов, то и длина будет [бесконечна] в отношении концов; если [время бесконечно] в отношении делимости, то и длина в отношении делимости; если время [бесконечно] в обоих [указанных отношениях], то в обоих [будет бесконечна] и величина.

Поэтому ошибочно рассуждение Зенона, в котором предполагается, что невозможно пройти бесконечное [множество предметов] или коснуться каждого из них в конечное время. Ведь длина и время и вообще все непрерывное называются бесконечными в двояком смысле: или в отношении деления, или в отношении концов. И вот, бесконечного в количественном отношении нельзя коснуться в конечное время, а бесконечного в отношении деления — можно, так как само время бесконечно именно в таком смысле. Таким образом, бесконечное удается пройти в бесконечное, а не в конечное время и коснуться бесконечного [множества можно] бесконечным, а не конечным [множеством]. Разумеется, невозможно ни пройти бесконечное в конечное время, ни конечное в бесконечное время, но если время будет бесконечным, то и величина будет бесконечной, и если величина, то и время.

Зенон же рассуждает неправильно.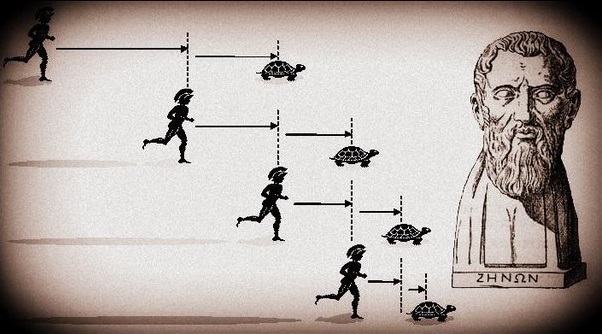 Если всегда — говорит он — всякое [тело] покоится, когда оно находится в равном [себе месте], а перемещающееся [тело] в момент «теперь» всегда [находится в равном себе месте], то летящая стрела неподвижна. Но это неверно, потому что время не слагается из неделимых «теперь», а также никакая другая величина.

Есть четыре рассуждения Зенона о движении, доставляющие большие затруднения тем, кто пытается их разрешить. Первое — о несуществовании движения на том основании, что перемещающееся [тело] должно дойти до половины прежде, чем до конца. Это [рассуждение] мы разобрали в предшествующих главах. Второе — так называемый «Ахиллес»: оно состоит в том, что самое медленное [существо] никогда не сможет быть настигнуто в беге самым быстрым, ибо преследующему необходимо прежде прийти в место, откуда уже двинулось убегающее, так что более медленное всегда должно будет на какое-то [расстояние] опережать [преследующего].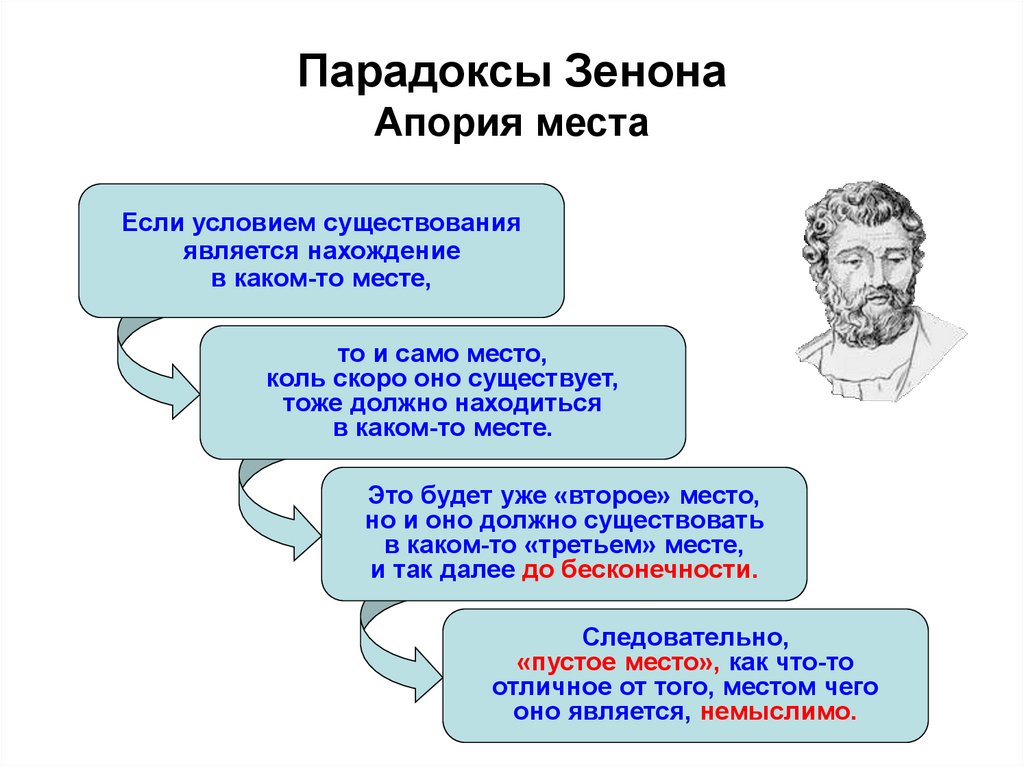

И это рассуждение основывается на делении пополам, отличается же [от предыдущего] тем, что взятая величина делится не на две равные части. То, что более медленное не настигается, вытекает из этого доказательства, но получается таким же путем, как и в [предшествующем] делении пополам (в обоих случаях то, что предел не достигается, получается вследствие определенного деления величины, только в данном случае прибавлено, что даже легендарное по своей быстроте [существо] не настигнет самое медленное), следовательно, и опровержение должно быть то же самое. Утверждение, что опережающее не может быть настигнуто, ошибочно: пока оно опережает, оно не настигается и все же будет настигнуто, если [Зенон] допустит [возможность] прохождения ограниченного [расстояния]. Таковы, следовательно, два [его] рассуждения.

Третье, о котором только что было упомянуто, состоит в том, что летящая стрела стоит неподвижно; оно вытекает из предположения, что время слагается из [отдельных] «теперь»; если это не признавать, силлогизма не получится.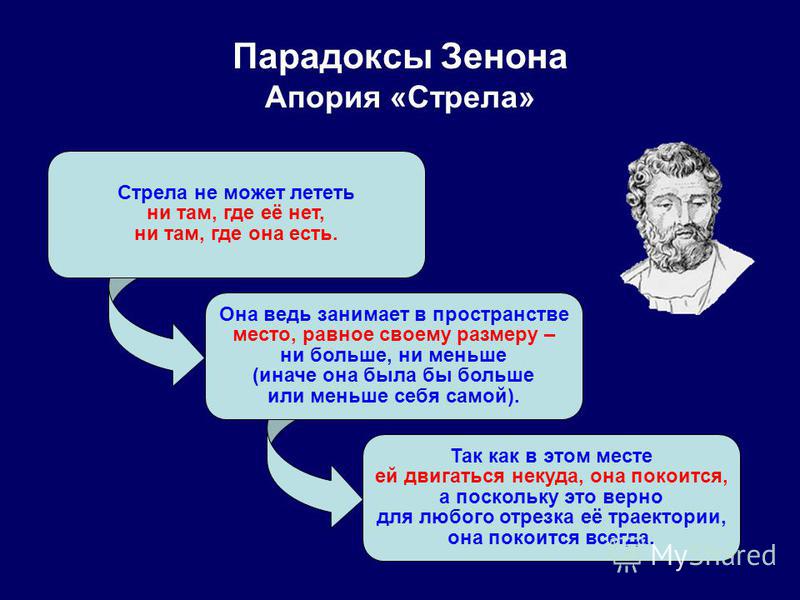

Четвертое [рассуждение] относится к равным предметам, движущимся по ристалищу с противоположных сторон мимо равных [неподвижных] предметов: одни [движутся] с конца ристалища, другие от середины, имея равную скорость, откуда, по его мнению, получается, что половина времени равна ее двойному количеству. Паралогизм состоит в том [предположении], что одинаковая величина, двигаясь с равной скоростью один раз мимо движущегося, другой раз мимо покоящегося [тела], затрачивает на это равное время, но это неверно. Допустим, например, что стоят неподвижные предметы АА…, другие — ВВ…, равные им по числу и величине, начинают движение от середины [ристалища], а предметы ГГ…, также равные прежним по числу и величине, [начинают движение] от конца, двигаясь с той же скоростью, что и В. Получится, что первое В и первое Г, двигаясь мимо друг друга, одновременно окажутся на [противоположных] концах [А].

Получится также, что Г пройдет мимо всех В, а В только мимо половины [А], следовательно, и время будет половинным, так как каждый предмет мимо каждого предмета проходит в одинаковое время. Вместе с тем выходит, что первое В прошло мимо всех Г, так как первое Г и первое В одновременно окажутся на противоположных концах [А], причем времени, как он, [Зенон], утверждает, для прохождения каждого В требуется столько же, сколько и на каждое А, так как те и другие в равное время проходят лишь А. Рассуждение, следовательно, таково, но результат получается вследствие упомянутой ошибки.

Таким же способом следует возразить тем, которые выдвигают рассуждение Зенона и полагают, что если всегда сначала надо пройти половину, а число половин бесконечно, то бесконечного пройти нельзя; или тем, которые формулируют это же рассуждение иначе, утверждая, что вместе с движением надо отсчитывать половину каждой возникающей половины, так что, пройдя все расстояние, приходится сосчитать бесконечное число, а это, по общему признанию, невозможно.

Историки пытаются реконструировать исходные рассуждения Зенона на основе пересказа Аристотеля. Понятно, что исходный текст по пересказу в точности восстановить невозможо. Я привел отрывки в русском переводе для того, чтобы вы могли отбросить реконструкции, являющиеся плодом воображения толкователей. Таких фантастических интерпретаций, имеющих мало общего с первоисточником, можно встретить достаточно.

Дихотомия

Первый вариант апории «Дихотомия»:

Пусть тело должно пройти путь конечной длины. Пусть оно уже прошло половину пути, отсчитаем эту половину. Далее надо отсчитать половину оставшегося пути, потом половину той половину и так далее. В результате надо отсчитать бесконечное число чисел. Представляется невозможным сосчитать бесконечное число величин за конечное время.

На данной схеме нарисовано тело — шар, который должен прокатиться по отрезку конечной длины и отмечены точки деления отрезка пополам:

Конечно, никто не стоит рядом с шаром и не отсчитывает расстояния синхронно с его движением. Имеется в виду, что невозможно просуммировать бесконечное число отрезков за конечное время. Допустим, общая длина пути равна 1 метру. Значит, отрезки будут длиной в 1/2 м, 1/4 м, 1/8 м, 1/16 м и т.д. Чтобы вычислить путь, надо просуммировать длины бесконечного числа отрезков:

1/2 + 1/4 + 1/8 + 1/16 +…

Конечно, во времена Зенона не умели вычислять суммы бесконечных рядов. Но это не значит, что суммы таких рядов не научились вычислять до сих пор. Подобная последовательность чисел называется геометрической прогрессией. Ее сумму умел вычислять, например, Ньютон. В школе тоже проходят эту формулу:

Сумма = a / (1 — q)

Где a — первый элемент последовательности (в рассмотренном случае 1/2 = 0,5). q — во сколько раз следующий элемент последовательности больше предыдущего (в рассмотренном случае тоже 0,5). Таким образом, сумма равна 0,5 / (1 — 0,5) = 0,5 / 0,5 = 1. Как видите, все сходится.

В школе приведенная формула может даваться без доказательств. Строгое ее обоснование дается в самом начале курса математического анализа в любом техническом ВУЗе (или в школе с математическим уклоном) в разделах «теория пределов» или «бесконечные последовательности». Каким же образом современные математики доказывают подобную формулу? Неужели они успевают просуммировать бесконечное число слагаемых за свою конечную жизнь? Нет, конечно. Совсем необязательно решать задачу «в лоб».

Я, разумеется, не буду цитировать здесь большой фрагмент учебника математики. Вместо этого я попытаюсь дать общее представление о доказательстве несколько упрощенно, показав общий принцип.

Берется предполагаемый результат суммы (в данном случае 1). Понятно, что при суммировании мы всякий раз будем получать суммы меньше единицы: 1 — 1/2, 1 — 1/4, 1 — 1/8,… . То есть, сумма не может находиться на числовой оси правее единицы.

Затем доказывается, что ни одно число слева от единицы тоже не подходит на роль суммы. Например, если взять число, равное 1 — 1/1000, то это число будет пройдено после 10-го деления отрезка пополам, когда сумма будет равна 1 — 1/1024. Так же можно рассуждать для любого другого числа, сколь угодно близкого к единице, но меньше нее.

Итак, справа от единицы нет ни одного подходящего числа, все они больше, чем нужно. Слева — тоже нет ни одного числа, все они меньше, чем нужно. Методом исключения выясняется, что искомый результат может быть равен только единице.

Чем больше величин мы просуммируем, тем ближе будет результат к единице. Оставшееся расстояние никогда не станет нулевым, но можно сделать его сколь угодно маленьким и указать, сколько слагаемых надо просуммировать, чтобы пройти любую заданную точку, близкую к единице.

Подобное действие в математике называется «пределом». В данном случае предел — число 1. Физика Ньютона использует понятие предела для решения многих задач. Например, через пределы определяются понятия скорости и ускорения. Как видите, в конечном счете законы движения в физике определяются через подобные пределы.

Итак, в первом варианте апории ошибка заключается в том, что заранее утверждается невозможность найти сумму. Сумму действительно нельзя найти таким способом, как указано в апории. Однако можно ее найти другим способом.

Второй вариант апории «Дихотомия»:

Для того, чтобы пройти путь конечной длины, надо сначала пройти половину. Для того, чтобы пройти оставшуюся половину, надо сначала пройти половину половины. И так далее. В результате надо пройти бесконечное число половин. Представляется невозможным пройти бесконечное число отрезков за конечное время.

Утверждается, что невозможно пройти бесконечное число отрезков за конечное время. В этом последнем утверждении и кроется ошибка в рассуждении и решение парадокса. Это утверждение о невозможности дается без доказательства, принимается как очевидное. Однако, то, что очевидно, не всегда истинно. Так и в этот раз - утверждение оказалось ложным. Расмотрим вопрос подробнее.

Все отрезки имеют разную длину, каждый последующий вдвое меньше предыдущего. Время, необходимое для преодоления отрезков, тоже будет уменьшаться. Если наш шар катится равномерно со скоростью 1 м/c, то первый отрезок будет пройден за полсекунды, второй — за четверть секунды, третий — за осьмушку и так далее. Если попытаться просуммировать отрезки времени, то получится та самая формула, которую мы уже видели:

1/2 + 1/4 + 1/8 + 1/16 +…

А эта формула, как мы знаем, дает вовсе не бесконечность, а 1. Так что время, необходимое для преодоления бесконечного числа отрезков, конечно (в данном случае 1 секунда).

Почему так получается? Да потому, что количество отрезков бесконечно велико, но время на преодоление каждого отрезка бесконечно мало. Говоря «поэтически», когда бесконечно большое сталкивается с бесконечно малым, то результат может быть и конечным, и бесконечным. В данном случае он конечен. А вот такая сумма будет уже бесконечной:

1/2 + 1/3 + 1/4 + 1/5 +…

А если избегать поэзии, то можно заметить: бесконечность — не является каким-то предметом. Бесконечности бывают самые разные. Мы уже рассмотрели несколько разновидностей. В конкретных случаях надо рассматривать конкретные формулы для той или иной бесконечности и доказывать свои суждения вместо того, чтобы заявлять: «это невозможно».

Итак, во втором варианте апории ошибка заключается в том, утверждается невозможность пройти бесконечное число отрезков за конечное время. На самом деле это иногда возможно при условии, что сами отрезки бесконечно малы.

Третий вариант апории «Дихотомия»:

Для того, чтобы тело прошло путь конечной длины, оно должно сначала коснуться места посредине пути. Для того, чтобы пройти оставийся путь, тело должно сначала коснуться места посредине оставшегося пути. И так далее. В результате тело должно коснуться бесконечного числа мест. Представляется невозможным коснуться бесконечного число числа мест за конечное время.

Этот вариант похож на предыдущий, только взамен преодоления отрезков предлагается «касаться мест». Ошибка также кроется в последнем утверждении. Оно бездоказательно. Хотя кому-то оно может показаться очевидным, но на деле оказывается ложным.

Чтобы коснуться точки на полпути шару нужно полсекунды. До следующей точки он доберется еще за четверть секунды.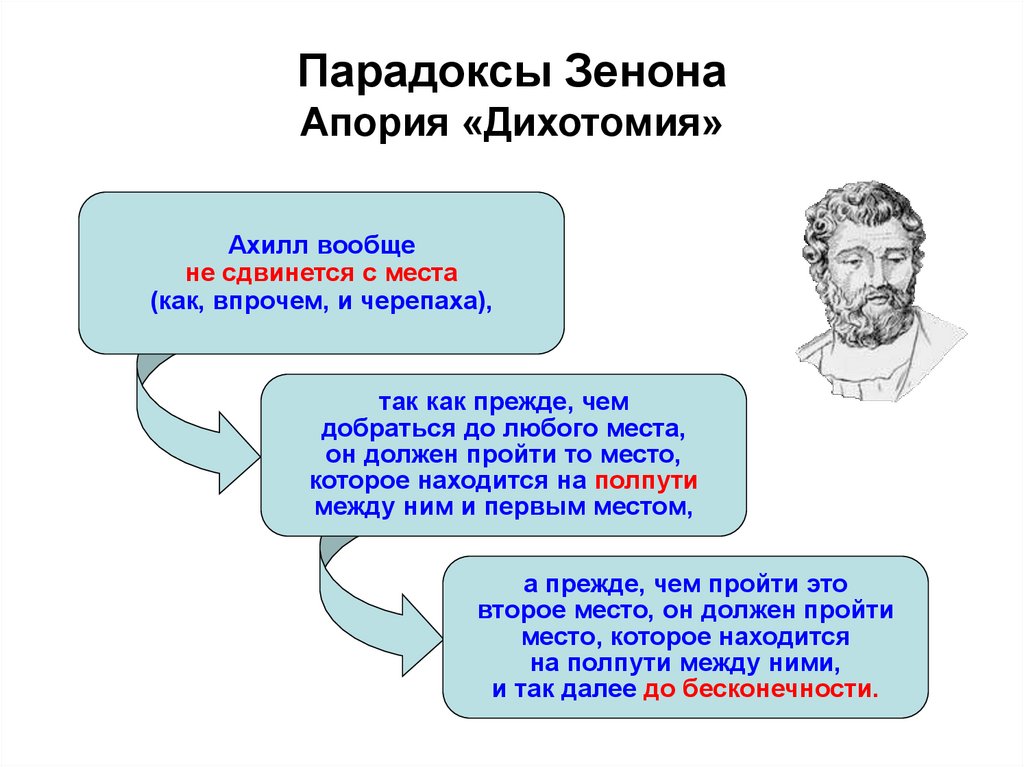 До следующей — за осьмушку и так далее. Да, число точек бесконечно велико, но время, нужное для касания каждой точки, бесконечно мало. Когда бесконечно малое сталкивается с бесконечно большим, результат не обязательно получится бесконечным. В данном случае он конечен.

Ахиллес и черепаха

Быстроногий Ахиллес никогда не сможет догнать черепаху, поскольку Ахиллесу необходимо сначала добежать до места, откуда начала движение черепаха, а она за это время немного уползет вперед до нового места. Ахиллес будет должен добежать до этого нового места, но черепаха за это время хоть немного, но уползет вперед. В результате окажется, что черепаха всегда будет на какое-то расстояние опережать Ахиллеса.

Ошибка тут точно такая же, как и в апории «Дихотомия». Утверждается (бездоказательно), что «черепаха всегда будет опережать», но что значит «всегда»? Бесконечное время? Однако, Ахиллес бежит быстрее. На рисунке видно, что каждый раз ему требуется преодолеть меньшее расстояние, чем на предыдущем шаге. То есть, время «догоняния» — бесконечно малая величина. А когда бесконечно большое (число «догоняний») сталкивается с бесконечно малым (временем «догоняния») то результат (общее время погони) не обязан быть бесконечным. Он и не бесконечен.

Допустим, что Ахиллес бежит в 10 раз быстрее (со скоростью 10 м/c) и расстояние до черепахи равно сначала 1000 метрам. Эти 1000 метров он пробежит за 100 секунд. Шустрая черепаха тем временем преодолеет 100 метров. Эти 100 метров Ахиллес пробежит за 10 секунд. Черепаха уйдет вперед на 10 метров. Эти 10 метров Ахиллес пробежит за 1 секунду. Получаем сумму:

100 + 10 + 1 + 1/10 + 1/100 +…

Снова имеем геометрическую прогрессию. Применим уже знакомую формулу:

a / (1 — q) = 100 / (1 — 1/10) = 100 / (9/10) = 1000/9

Как видите, время вовсе не бесконечно, если его подсчитать, а не голословно утверждать, дескать, «никогда».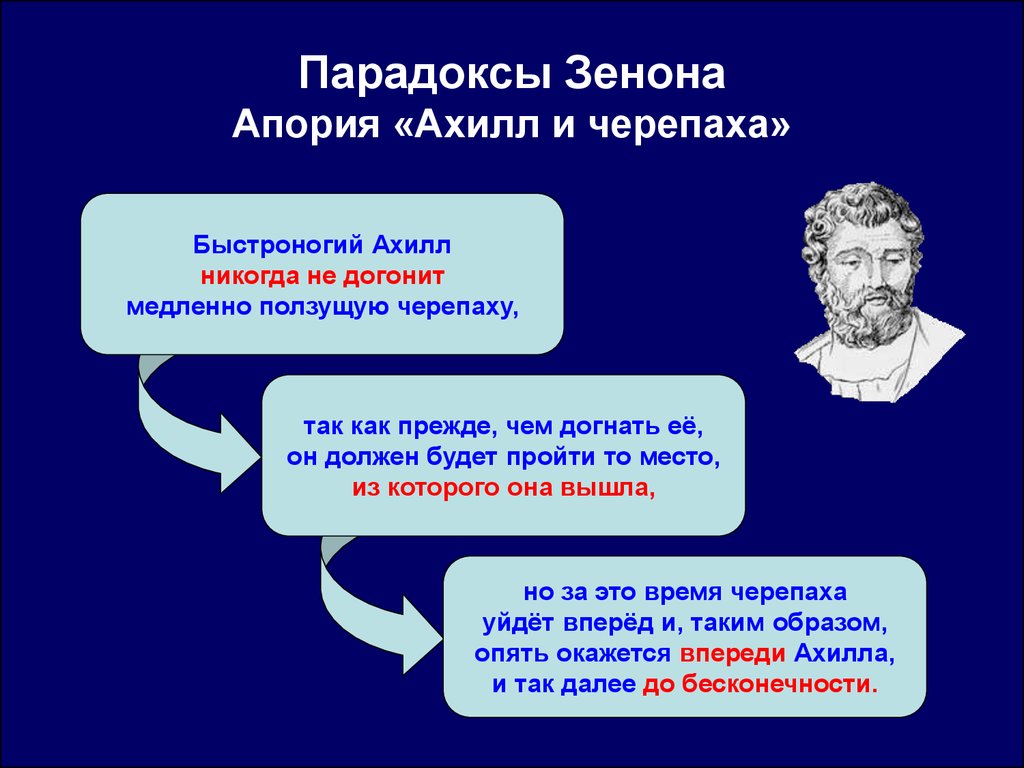

Стрела

В двух предыдущих случаях Зенон исходил из предположения, что время и расстояние можно делить бесконечно. Как сказали бы в наше время, время и пространство непрерывны. А что, если время и пространство состоят из мельчайших кирпичиков, и делить можно только до определенного предела — до этих кирпичиков? Примерно как кусок железа можно разделить до атомов, но не более того (если делить дальше, это будет уже не железо) или как изображением на экране компьютера можно управлять с точностью только до пиксела.

Я недаром упомянул изображение на компьютере. Движущиеся фигурки на экране монитора — отличная иллюстрация дискретного пространства и времени. Расстояния определяются с точностью до 1 пиксела, и более мелкими деталями изображения мы управлять не можем. Время тоже определяется с точностью до 1 кадра (например 1/100 секунды если монитор имеет частоту развертки 100 Герц). Компьютерная графика поможет нам понять логику решения двух других парадоксов Зенона. Рассмотрим их.

Пусть время делится на отдельные кадры. неподвижная стрела в каждом кадре занимает место, равное ее длине. Летящая стрела в каждом кадре также занимает место, равное ее длине, а значит, не летит, а покоится.

Аристотель предлагает такое решение этого парадокса: давайте, мол, не будем признавать, что время делится на отдельные моменты. Но это — не решение, а уход от него. Мы решим парадокс «честно». Пусть время состоит из отдельных минимальных фрагментов (как кадры на экране монитора). Где тогда ошибка в парадоксе?

А вот она: «а значит, не летит, а покоится.» Из того, что летящая стрела имеет некоторое общее свойство с неподвижной стрелой (занимать место, равное ее длине) нельзя делать вывод, что речь идет в обоих случаях об одинаковых стрелах. Ведь другие свойства могут оказаться различными! И в самом деле: между стрелами есть разница: если неподвижная стрела занимает в каждом кадре одни и те же 100 пикселов, то летящая стрела может в следующем кадре занимать другие 100 пикселов. По этому свойству стрелы различаются.

Здесь мы видим еще одно подтверждение правила «аналогии лгут». Нелогично из сходства объектов в одном свойстве делать вывод о сходстве по всем свойствам.

Стадион

Апория «Стадион» (в приведенном выше фрагменте перевода не стадион, а ристалище) также рассматривает ситуацию, когда время нельзя делить до бесконечности, а только до минимального фрагмента (кадра).

Пусть есть три группы предметов, одинаковых по количеству (N штук). Один ряд «A» стоит на месте. Второй ряд «B» марширует мимо него слева направо, а третий ряд «C» марширует мимо первого ряда справа налево. Пусть ряд «B» минует за один кадр одного из ряда «A», так что ему требуется N кадров. Также ряду «C» надо N кадров, чтобы пройти мимо ряда «B». Но второй и третий ряды маршируют навстречу друг другу, так что должны миновать друг друга за время, вдвое меньшее — N/2 кадров.

В качестве движущихся предметов возьмем следующих друг за другом лошадей. На рисунке вы видите 6 последовательных кадров. Верхний ряд лошадей «A» стоит на месте. Следующий ряд «B» идет справа налево. И самый нижний ряд «C» движется слева направо. Обратите внимание на первую лошадь во ряду «B». На кадрах 2, 3, 4 и 5 она побывала перед каждой из лошадей ряда A. Однако она успела побывать только перед двумя лошадьми из ряда «C» (на кадрах 4 и 5).

Ошибку в этом парадоксе нашел сам Аристотель в своем пересказе. Как он правильно заметил, утверждается, что «величина, двигаясь с равной скоростью один раз мимо движущегося, другой раз мимо покоящегося [тела], затрачивает на это равное время, но это неверно». Лошадь из ряда «B» за один кадр минует не одну, а сразу две лошади из ряда «C».

Таким образом, причина этого парадокса — ложное утверждение «Также ряду «C» надо N кадров, чтобы пройти мимо ряда «B». Можно догадаться, откуда оно взялось. Если рассматривать непрерывное движение, то каждая лошадь ряда B обязательно побывает перед каждой лошадью ряда C. Этот факт распространяется и на дискретное движение. В результате имеем скрытое смешивание двух разных моделей и противоречие. Правильное рассуждение соответствует рисунку.

---

В заключение отмечу тот факт, что логические ошибки, лежащие в основе парадоксов, могли быть обнаружены еще во времена Зенона. Например, тогда не умели считать сумму бесконечной геометрической прогрессии, но можно было заметить, что утверждение «чтобы преодолеть бесконечное число отрезков, требуется бесконечное время» — принимается без доказательства.

Судя по приведенным фрагментам, Аристотель пытался разобраться с этим вопросом.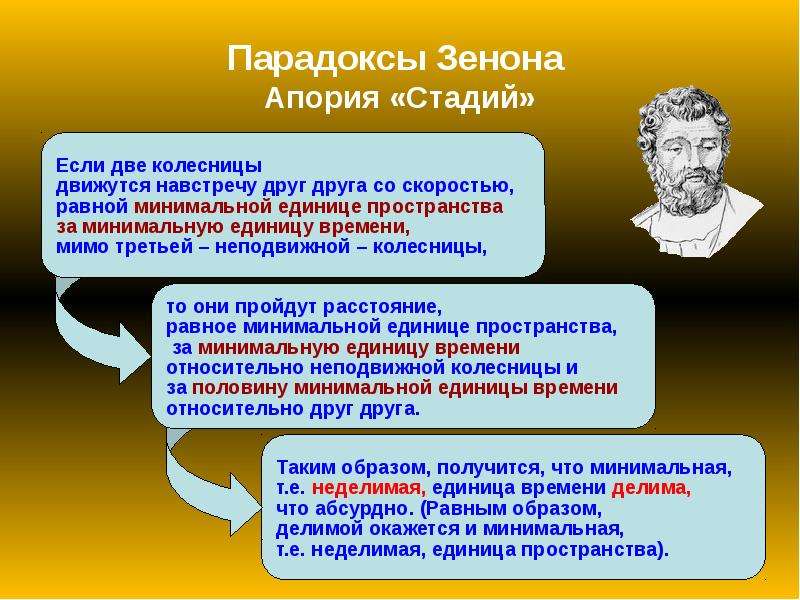 Можно услышать такие мнения, что Зенон пытался опровергнуть апориями (так сказать, «от противного») какие-то заблуждения современников. Это, конечно, — досужие домыслы, поскольку все, что у нас есть — пересказ Аристотеля. В любом случае в рассуждениях апорий имеются логические ошибки, которые не позволяют применять их даже для доказательства «от противного».

материалы, оборудование и технологии для рекламного производства

• Каталог товаров

  Каталог товаров

  Перейти в развернутый каталог

  Каталоги PDF

  РАСХОДНЫЕ МАТЕРИАЛЫ

  • Шелкотрафаретные материалы
  • Светотехника рекламная и декоративная
  • Химия (клеи, краски, лаки, спецхимия, очистители)
  • Монтажные и упаковочные материалы
  • Алюминиевые и пластиковые профили
  • Материалы и оборудование DTF
  • Чернила для цифровой печати
  • POS-материалы и оборудование, системы Joker, Uno и Tritix
  • Мобильные стенды, Флагштоки, Штендеры, Стойки-ограждения
  • Жесткие листовые материалы
  • Цветные самоклеящиеся плёнки
  • Материалы для печати и ламинации
  • Световозвращающие материалы
  • Термотрансферные материалы
  • Сувенирная и наградная продукция
  • Одежда и аксессуары для маркировки
  • CRAFT-материалы и оборудование

  ОБОРУДОВАНИЕ И ИНСТРУМЕНТЫ

  • Принтеры для рекламных производств
  • Принтеры для полиграфии и печати трансферов
  • 3D принтеры
  • Оборудование для раскроя и резки
  • Фрезерно-гравировальное оборудование и лазерные граверы
  • Оборудование для печати на ткани
  • Футболочные принтеры
  • Ламинаторы
  • Термопрессы
  • Электроинструмент
  • Алюминиевые лестницы и стремянки
  • Оборудование для производства букв из жидкого акрила
  • Триммеры, абразивы, инструменты для работы с плёнками
  • Люверсы и инструмент для их установки
  • Ножи, лезвия, ножницы, коврики
  • Шелкотрафаретное оборудование
  • Запчасти, доп. оборудование и программное обеспечение
  • Зенон-Академия
    • Видео
    • Статьи
    • План вебинаров
  • О нас
    • О компании
    • Наши сотрудники
  • Новости
    • Новости
    • Акции
    • Новинки
  • События
    • Семинары
    • Выставки
    • Поздравления
    • Вебинары
  • Сервис
    • Расчет вывески
    • Сервисная служба
  • Условия работы
    • Доставка
    • Оплата
  • Контакты

  Вы используете устаревший браузер

  Для того, чтобы использовать все возможности сайта,
  загрузите и установите один из браузеров:

  Google Chrome

  скачать последнюю версию

  Opera

  скачать последнюю версию

  Mozilla

  скачать последнюю версию

  Яндекс Браузер

  скачать последнюю версию

  артикул

  Подписка на рассылку

  Письмо с подтверждением действий отправлено на указанный вами email.

  Пожалуйста, следуйте инструкциям указанным в письме.

  Извините, произошла ошибка, сервис попробуйте воспользоваться сервисом позднее.

  Для подписки на рассылку, заполните, пожалуйста ВСЕ поля формы

  Регионы подписки

  • Москва — Лосиный остров
  • Москва — Гольяново
  • Подмосковье — Одинцово
  • Подмосковье — Подольск
  • Архангельск
  • Барнаул
  • Белгород
  • Владивосток
  • Владимир
  • Волгоград
  • Воронеж
  • Екатеринбург
  • Ижевск
  • Иркутск
  • Казань
  • Калининград
  • Краснодар
  • Красноярск
  • Курск
  • Липецк
  • Нижний Новгород
  • Новосибирск
  • Омск
  • Оренбург
  • Пенза
  • Пермь
  • Пятигорск
  • Ростов-на-Дону
  • Рязань
  • Самара
  • Санкт-Петербург
  • Саранск
  • Саратов
  • Симферополь
  • Смоленск
  • Сочи
  • Ставрополь
  • Тамбов
  • Тольятти
  • Томск
  • Тула
  • Тюмень
  • Ульяновск
  • Уфа
  • Хабаровск
  • Чебоксары
  • Челябинск
  • Якутск
  • Ярославль

  Я согласен(-на) на обработку персональных данных

  Заявка на товар:

  Вы можете отправить данную форму заявки на товар, либо связаться с нами по телефону или по E-mail , сообщив менеджеру артикул .

  Заявка отправлена

  Мы позвоним Вам в ближайшее время!

  Необходимо пройти тест Тьюринга (капчу).

  Номер телефона

  Город

  Выберите городМосква — Лосиный островМосква — ГольяновоПодмосковье — ОдинцовоПодмосковье — ПодольскАрхангельскБарнаулБелгородВладивостокВладимирВолгоградВоронежЕкатеринбургИжевскИркутскКазаньКалининградКраснодарКрасноярскКурскЛипецкНижний НовгородНовосибирскОмскОренбургПензаПермьПятигорскРостов-на-ДонуРязаньСамараСанкт-ПетербургСаранскСаратовСимферопольСмоленскСочиСтавропольТамбовТольяттиТомскТулаТюменьУльяновскУфаХабаровскЧебоксарыЧелябинскЯкутскЯрославль

  Я согласен(-на) на обработку персональных данных

  Замечания и предложения

  Если вы столкнулись с ситуацией, в которой не смогли получить ответ или нужную вам помощь от наших сотрудников, остались недовольны сервисом или не нашли решения своего вопроса, то можете напрямую обратиться со своей проблемой к руководству компании.

  Просим вас наиболее полно и информативно описать возникшую ситуацию, указать филиал, фамилию и имя сотрудника / сотрудников с которыми вы работали и прочую информацию.

  Также мы будем рады любым предложениям и пожеланиям по улучшению нашей работы.

  Surname

  Номер телефона

  City

  Выберите городМосква — Лосиный островМосква — ГольяновоПодмосковье — ОдинцовоПодмосковье — ПодольскАрхангельскБарнаулБелгородВладивостокВладимирВолгоградВоронежЕкатеринбургИжевскИркутскКазаньКалининградКраснодарКрасноярскКурскЛипецкНижний НовгородНовосибирскОмскОренбургПензаПермьПятигорскРостов-на-ДонуРязаньСамараСанкт-ПетербургСаранскСаратовСимферопольСмоленскСочиСтавропольТамбовТольяттиТомскТулаТюменьУльяновскУфаХабаровскЧебоксарыЧелябинскЯкутскЯрославль

  Сообщение

  Я согласен(-на) на обработку персональных данных

  • все филиалы

  Заказать обратный звонок

  City

  Выберите городМосква — Лосиный островМосква — ГольяновоПодмосковье — ОдинцовоПодмосковье — ПодольскАрхангельскБарнаулБелгородВладивостокВладимирВолгоградВоронежЕкатеринбургИжевскИркутскКазаньКалининградКраснодарКрасноярскКурскЛипецкНижний НовгородНовосибирскОмскОренбургПензаПермьПятигорскРостов-на-ДонуРязаньСамараСанкт-ПетербургСаранскСаратовСимферопольСмоленскСочиСтавропольТамбовТольяттиТомскТулаТюменьУльяновскУфаХабаровскЧебоксарыЧелябинскЯкутскЯрославль

  Я согласен(-на) на обработку персональных данных.

  Статья об Апории из «Свободного словаря»

  Следующая статья взята из Большой советской энциклопедии (1979). Он может быть устаревшим или идеологически предвзятым.

   

  термин, использовавшийся древнегреческими философами для обозначения проблем, которые было трудно или невозможно решить. Эти проблемы чаще всего связаны с противоречиями, существующими между фактами наблюдения и опыта, с одной стороны, и попытками их интеллектуального анализа, с другой.

  Самые известные апории возникли у Зенона Элейского, жившего в пятом веке г. до н.э. г. . Они излагаются в различных позднейших редакциях, часто противоречащих друг другу, так как подлинные рассуждения самого Зенона не сохранились. Апория «против множественности предметов» ставит вопрос о возможности умственного постижения вещей во множественном числе. Мнение, что такая концепция невозможна из-за ее противоречивости, приписывается Зенону. Если вещь есть множество, то это бесконечное множество, так как третья вещь нужна для того, чтобы разделить две вещи и т. д.; но тогда вещь конечных размеров должна либо иметь бесконечные размеры (если ее составные части имеют размеры), либо не иметь размеров (если ее составные части не имеют измерений). В этой апории проявляется «парадокс меры», демонстрирующий трудность логически непротиворечивого представления пролонгированных измерений в виде совокупности нульмерных точек. Другой вариант этой апории демонстрирует противоречие между утверждениями о конечном и бесконечном качестве множества реально существующих вещей. Оба утверждения, кроме того, могут считаться оправданными.

  «Дихотомия», «Ахиллес», «Стрела» и «Стадион» — апории, посвященные трудностям, связанным с понятием движения. «Дихотомия» утверждает, что прежде чем движущееся тело сможет пройти весь путь, оно должно пройти половину пути; до этого четвертый и так далее. Но поскольку этот процесс интеллектуального деления бесконечен, движение никогда не может начаться. Другой вариант той же апории заключает, что движение никогда не может закончиться. Это противоречие ставит вопрос о правильности представления понятий пространства, времени и движения с помощью таких математических абстракций, как точка и отрезок, а также о спорности различных абстракций о бесконечности. В одной из самых популярных апорий «Ахиллес» есть анализ противоречия между очевидными фактами чувственного опыта и рассуждениями, согласно которым быстрый Ахиллес не может догнать черепаху. Причина этого в том, что пока Ахиллес пытается догнать черепаху, черепаха также успевает продвинуться на некоторое расстояние, и пока Ахиллес покрывает это расстояние, черепаха ползет чуть дальше и так далее. Апория под названием «Стрела» показывает трудности изображения движения, возникшие из-за принятия «атомистических» представлений. Если считать, что пространство, время и сам процесс движения состоят из неких «неделимых» элементов, то внутри одного такого «неделимого» элемента тело двигаться не может (иначе «неделимый» элемент был бы «разделен»), а потому оно и двигаться вообще не может (сумма «покоев» не может складываться в движение). Это означает, что летящая стрела «фактически» покоится.

  Апории Зенона подчеркивают относительный и противоречивый характер математических описаний реальных процессов движения, несостоятельность претензий на «адекватность» («изоморфизм») всех без исключения математических представлений о физических процессах и, наконец, спорность общепринятые мнения о взаимно однозначной определенности фигурирующих в этих представлениях понятий, как, например, натуральный числовой ряд. В частности, логические противоречия, устанавливаемые в «Дихотомии» и «Ахиллесе», могут быть объяснены несостоятельностью «очевидного» предположения, что последовательности точек, фигурирующих в этих апориях, дадут один и тот же естественный ряд, что и их мысленные ряды. изображения, то есть числа, обозначающие эти точки. Уверенность в бесспорности этого предположения была подорвана развитием так называемых нестандартных, или взаимно неизоморфных, моделей теории чисел.

  Ни одно из решений, предложенных для разрешения противоречий апорий, не может в настоящее время считаться общепринятым. Проблемы, связанные с апориями, продолжают интенсивно обсуждаться; в том числе работы советских ученых. Влияние апорий Зенона отчетливо прослеживается, например, в положениях античного скептицизма и в так называемых антиномиях чистого разума И. Канта. В целом анализ апорий, являющихся своего рода негативным выражением диалектики взаимосвязи реального мира и его отражения в мышлении, оказал важное влияние на последующее развитие логики и теории познания.

  ЛИТЕРАТУРА

  Яновская С.А. «Апории Зеноны Елейскогоисовременнауки». В книге Философская энциклопедия , т. 2. Москва, 1962. С. 170–174.
  Яновская С. А. «Преодолены жизни в современной науке трудности, известные под названием «Апории Зенона»?» В сборнике Проблемы логики . Москва, 1963. С. 116–136.
  Петров Ю.В. A. Логические проблемы абстракции бесконечности и жизнедеятельности . М., 1967.
  Френкель А., Бар-Гилель Я.. Основная теория множеств . М., 1966. С. 23, 26–27. (Перевод с английского; содержит библиографию и примечания редактора. )

  I U А. Г АСТЕВ , В. А. К ОСТЕЛОВСКХ , и I U . А. П ЭТРОВ

  Большая советская энциклопедия, 3-е издание (1970-1979). © 2010 The Gale Group, Inc. Все права защищены.

  Зенон из Элеаза. Апория Зенона з Элей. Школа элитарная

  Zenon z Elei jest старожизненный филозофем греческий, который был учнем Парменидеса, przedstawiciela szkoły Eleatic. Уродзил сие около 490 пнэ. е. w południowych Włoszech, w mieście Elay.

  С чего слынон Зенон?

  Аргументы Зенона славят эту философию якоспритного полемиста с душой софистики. Treść nauk tego myśliciela została uznana za identyczną z ideami Parmenidesa. Элеатская школа (Ксенофан, Парменид, Зенон) шутка прекурсорем софистики. Zenon był tradycyjnie uważany za jedynego «ucznia» Parmenidesa (chociaż Empedokles był również nazywany jego «następcą»). Мы wczesnym dialogu nazwanym «Софист» Аристотель nazwał «wynalazcą диалектики» Зенон. Użył pojęcia «dialektyki», najprawdopodobniej w sensie dowodów z niektórych ogólnie akceptowanych przesłanek. В шутку одданы працы Аристотелеса «Топека».

  W «Федру» Platon mówi o doskonałym właścicielu»sztuka mówienia» «Eleatic Palamedes» (co oznacza «sprytny wynalazca»). Plutarch pisze o Zenonie, używając terminologii używanej do opisania sofistycznej praktyki. Mówi, że filozof ten był w stanie obalić, prowadząc do aporii przez contrargumenty. Wskazówką, że studia Zenona miały charakter sofistyczny, jest wzmianka w dialogu Alkibiadesa I, że filozof ten wziął wysoką opłatę za nauczanie. Диоген Лаэртиус Моуи, że po raz pierwszy Dialogi zaczęły pisać Zeno z Elei. Ten myśliciel był również uważany za nauczyciela Peryklesa, słynnego polityka Aten.

  Polityka Zenona

  Możesz znaleźć raporty od Doxographers, żeZeno zajmował się polityką. Na przykład wziął udział w konspiracji przeciwko neharkhovi, tyranowi (istnieją inne warianty jego imienia), został aresztowany i probował odgryźć go w uchu podczas przesłuchania. Historia та została przedstawiona przez Diogenesa на тему Heraklida Lemba, który z kolei odnosi się do książki o perypatektach satyry.

  Wielu historyków starożytności przekazywało raportyupór na dworze tego filozofa. Tak więc, według Antistenesa z Rodos, Zeno Eleajsky odgryzł mu język. Hermipp mówi, że filozof został wrzucony do moździerza, w którym został ogłuszony. Десять эпизодов были настойчивыми бардзо популярными в литературной старости. Воспоминания о Плутархе Иеронее, Диодоре из Сицилии, Флавии из Филострату, Клеменсе из Александрии, Тертуллиане.

  Dzieła Zenona

  Zeno Eleiski był autorem prac «PrzeciwFilozofowie „” Kontrowersje „” Interpretacja Empedokles «i» Na łonie natury „Jest jednak możliwe, że wszystkie z nich, z wyjątkiem” Interpretacja Empedokles „były w rzeczywistości wariantów nazwą jednej książce. W” Parmenides „Plato odnosi się do kompozycji, napisany przez Zeno w celu ośmieszenia przeciwników swego nauczyciela i pokazać, że nawet bardziej absurdalne wnioski wynikające założenie ruchu i zestawy niż uznaniu pojedynczej istoty Parmenidesa. rozumowanie filozof znany jako prezentowane przez późniejszych autorów. To Arystoteles ( esej „Fizyka”) и его комментаторы (n Na przykład, Simplijusz).

  Argumenty Zeno

  Główne dzieło Zeno zostało skompilowane,najwyraźniej z zestawu wielu argumentsów. Aby udowodnić przeciwnie, ich logiczna forma została zmniejszona. Ten filozof, broniąc postulat stacjonarnego pojedynczego bytu, który wysunął szkoły Eleatic (Zeno, według niektórych badaczy, zostały stworzone w celu wspierania nauczania Parmenides), starał się wykazać, że naprzeciwko dodatek teza (o ruchu i ustawić) nieuchronnie prowadzi do Absurd musi zatem zostać odrzucony przez myślicieli.

  Zeno oczywiście przestrzegał prawa «wykluczonych»Po trzecie „: jeśli oświadczenie dwie przeciwne nie jest prawdziwe, to prawda więcej wiadomo na temat tych dwóch grup, które filozof argumenty (Zenon z Elei): .. przed ruchem i przed różnymi Ponadto , istnieje dowód, który wskazuje, że argumentsy przeciw percepcji zmysłowej i przeciwko miejscu.

  Argumenty Zenona przeciwko setowi

  Simplica zachowała te arguments. Cytuje Zeno w komentarzu делать «Физики» Аристотелеса. Proclus mówi, że skład interesującego nas myśliciela zawierał 40 подобнейших аргументов. Pięć z nich wymieniamy.

  1. Broniąc swojego nauczyciela, którym był Parmenides,Zenon z Eleuskiego mówi, że jeśli istnieje zbiór, to zatem rzeczy muszą być konieczne, wielkie i małe: są one tak małe, że nie mają żadnej wartości i są tak wielkie, że są nieskończone .

     Dowód jest następujący . Pewna wartość musi mieć istniejącą. Będąc do czegoś dodanym, zwiększy to i zmniejszy, będąc zabranym. Aby jednak odróżnić się od innych, trzeba bronić się przed nim, być na pewnej odległości. Oznacza to, że zawsze będzie jedna trzecia między dwoma istotami, przez które są różne. Musi być różny od innych itd. Ogólnie rzecz biorąc, bycie bedzie nieskończenie wielkie, ponieważ jest to suma rzeczy, które są nieskończone w liczbie. Filozofia szkoły Eleatic (Parmenides, Zeno и т. п.) Opiera się na tej myśli.

  2. Jeśli jest zestaw, to rzeczy beędą nieograniczone i ograniczone.

     Довод. : jeśli jest ich wiele, jest tak wiele rzeczy,ilu ich jest, nie mniej i nie więcej, to jest ich liczba jest ograniczona. Jednak w tym przypadku zawsze bedą inni między rzeczami, między którymi z kolei są trzecimi itd. Oznacza to, że ich liczba będzie nieskończona. Ponieważ jednocześnie udowodniono przeciwność, pierwotny postulat jest nieprawidłowy. Oznacza to, że zestaw nie istnieje. Jest to jedna z głównych idei, która rozwija Parmenides (szkoła elitarna). Zeno ją wspiera.

  3. Jeśli jest zestaw, to rzeczy na razmusi być nieporównywalna i podobna, co jest niemożliwe. Według Platona, десять аргументов rozpoczął księgę filozofa zainteresowania. Ta aporia zakłada, że ​​jedno i to samo jest postrzegane jako podobne do siebie i różne od innych. W Platonie jest on rozumiany jako paralogizm, ponieważ niekompetencja i podobieństwo są podejmowane na różne sposoby.
  4. Zauważamy interesujący аргумент przeciwko temu miejscu. Zeno powiedział, że jeśli jest jakies miejsce, to powinno być w czymś, ponieważ odnosi się do wszystkiego, co istnieje. Wynika z tego, że miejsce również będzie na miejscu. Я так w nieskończoność до бесконечности. Wniosek: nie ma miejsca. Аргумент десять Arystoteles я его komentatorzy odnosili się сделать liczby paralogizmów. Błędem jest to, że «być» oznacza «być na miejscu», ponieważ w pewnym miejscu nie ma bezcielesnych pojęć.
  5. Przeciw argumentsowi percepcji zmysłównazywane «ziarnem prosa». Jeśli jedno ziarno lub jego tysięczna część, podczas upadku, nie wytwarza hałasu, jak może spaść w kierunku medycznym? Jeśli rdzeń ziarna wytwarza hałas, stąd też musi odnosić się do jednej tysięcznej, co w rzeczywistości nie ma miejsca. Десять аргументов dotyka Problemu progu percepcji naszych narządów zmysłów, chociaż jest sformułowany w kategoriach całości i części. Paralogizm w tym sformułowaniu polega na tym, że jest to «hałas wytwarzany przez część», który w rzeczywistości nie jest (zgodnie z uwagą Arystotelesa istnieje on w możliwości).

  Argumenty Against Motion

  Najbardziej znane były cztery aporieZeno Elei przeciw czasowi i ruchowi, znane z Arystotelesowskiej «Fizyki», а также komentarze Johna Philopona i Simpliciusa на десять тем. Pierwsze dwa z nich opierają się na fakcie, że odstęp dowolnej długości można przedstawić jako nieskończoną liczbę niepodzielnych «miejsc» (części). Nie można go przekazać w momencie zakończenia. Trzecie i czwarte aporie są oparte na tym, że czas składa się z niepodzielnych części.

  «Dychotomia»

  Rozważ Аргумент «Etapy» («Dychotomia» — «inna nazwa). Przed pokonanie pewnej odległosci, przesuwającclęs -przhe -przhe -przhe -przhe -wrzhe -wrzhe- przhe- przhe -przhe- przhe -przhe -przhe- nieskończoność, bo każdy segment może być podzielona na pół, bez względu na to jak był mały.

  Innymi słowy, ponieważ zawsze istnieje ruchjest realizowany w przestrzeni, a jego kontinuum jest uważane za nieskończony zbiór różnych segmentów, co jest faktycznym danym, ponieważ każda ciągła wielkość jest nieskończenie podzielna. W konsekwencji ruchomy corpus bedzie musial przejść przez skończoną liczbę segmentów, co jest nieskończone.To uniemożliwia ruch.

  «Achilles»

  Jeśli jest ruch, najszybszy biegacznigdy nie będzie w stanie nadrobić zaległości z najwolniejszymi, ponieważ konieczne jest, aby dawni nadrabiali zaległości, aby dotrzeć do miejsca, z którego uciekający mężczyzna zaczął się poruszać. Dlatego, jeśli to konieczne, biegacz powinien zawsze być trochę przed nami.

  Rzeczywiście, przenoszenie oznacza przejście zjeden punkt do otherego. Z szybki Achilles zaczyna dogonić żółwia, który jest obecnie w punkcie B. Po pierwsze, musi przejść w połowie drogi, czyli odległość AAh. Kiedy Achilles znajduje się w punkcie AL, podczas wykonywania ruchu żółw przejdzie trochę dalej do segmentu VVH. Wtedy biegacz, który jest na środku swojej drogi, będzie musial dotrzeć do Bb. W tym celu konieczne jest przekazanie połowy odległości A1B. Kiedy zawodnik znajduje się w połowie drogi do tego celu (A2), nieco dalej żółw się czołgnie. Я беру далей. Zenon Eleusa w obu aporiach sugeruje, że kontinuum dzieli się na nieskończoność, myśląc jako rzeczywistą istniejącą tę nieskończoność.

  «Strzałka»

  W rzeczywistości, latająca strzała odpoczywa, wierzyłaZeno z Eleaz. Filozofia tego naukowca zawsze miała uzasadnienie, a ta aporia nie jest wyjątkiem. Dowód jest następujący: strzałka za każdym razem zajmuje miejsce równe jej objętości (пониев стрзалка были нигдзие «нигдзие»). Jednak zajęcie miejsca równego sobie oznacza bycie samotnym. Stąd można wywnioskować, że ruch można rozumieć tylko jako sumę różnych stanów spoczynku. Jest to niemożliwe, ponieważ nic nie dzieje się z niczego.

  «Ciała ruchome»

  Jeśli występuje ruch, można zauważyć następujące. Jedna z dwóch wielkości, które są równe i poruszają się z tą samą prędkością, przejdzie w równym czasie dwukrotnie większym odległości, a nie równym otheru.

  Ta aporia została tradycyjnie wyjaśniona za pomocąrysunek. W kierunku siebie poruszają się dwa równe obiekty oznaczone symbolami literowymi. Idą równoległymi ścieżkami i mijają w tym samym czasie trzeci obiekt, który jest im równy pod względem wielkości. Przemieszczając się z tą samą prędkością, jeden raz po odpoczynku, a otheri — poza poruszającym się obiektem, ta sama odległość bedzie przemierzana jednocześnie przez okres czasui. Niepowtarzalny moment w tym przypadku będzie dwa razy większy od niego samego. Шутка на логические niepoprawne. Musi być albo podzielna, albo niepodzielna część pewnej przestrzeni musi być podzielna. Ponieważ Zeno nie przyznaje się do żadnej z tych rzeczy, konkluduje zatem, że ruchu nie można myśleć bez sprzeczności. To znaczy, że nie istnieje.

  Wniosek z wszystkich aporii

  Wniosek, który został złożony ze wszystkich aporii,opracowany w celu wspierania idei Parmenidesa, Zenona, to jest, że przekonuje nas o istnieniu ruchu i różnych dowodów zmysłów nie zgadzają się z argumentami powodu, że to sprzeczność sama w sobie nie zawiera, a więc są prawdziwe. Fałsz w tym przypadku powinien być rozumiany na podstawie rozumowania i uczuć.

  Przeciw komu wysłano aporie?

  Jedyną odpowiedzią jest pytanie, przed którym aporiaZeno zostały wysłane, nie ma. W literaturze wyrażono punkt widzenia, w którym arguments tego filozofa były skierowane przeciw zwolennikom «matematycznego atomizmu» Pitagorasa, które to fizyczne ciała zbudowane są z punktów geocznych i wierzyły, że czas ma struct. Obecnie ten Pogląd nie ma zwolenników.

  В старожильных традициях известно о том, что они zasugerował powrót do Platona, że ​​Zeno bronił idei swego nauczyciela. Его przeciwnicy были zatem wszystkim, którzy nie podzielali doktrynę, która przedstawiła szkołę Eleatic (Parmenides, Zenon) i utrzymywane na podstawie dowodów zdrowego rozsądku.

  Więc rozmawialiśmy или kim jest ZenoEleatic. Jego aporie zostały krótko zbadane. A dziś diskusje na temat struktury ruchu, czasu i przestrzeni są dalekie od ukończenia, więc te interesujące pytania pozostają otwarte.