Законы движения планет Солнечной системы

Вы уже знаете, что революционная идея Николая Коперника о гелиоцентрической системе мироустройства дала невероятный толчок развитию астрономии. Однако, если вы помните, Коперник в своём учении не отказался от мыслей Аристотеля о «совершенстве» орбит планет. Поэтому для объяснения многих явлений (например, попятного движения планет), в его теории всё ещё присутствовали эпициклы и деференты.

При этом многие учёные считали, что движение небесных тел должно быть равномерным и по «самой совершенной кривой», то есть окружности. Поэтому до конца XVI века им не удавалось точно рассчитать относительное положение планет на несколько лет вперёд. Теория давала заметное расхождение с результатами наблюдений.

Лишь в начале XVII века австрийский астроном Иоганн Кеплер открыл кинематические законы движения планет. В своих поисках он исходил из убеждения, что «в мире правит число», высказанного ещё Пифагором. Кеплер пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон, описанных и вписанных в орбиты планет многоугольников и так далее.

Но увы, каждый раз сравнив свою модель с наблюдаемыми орбитами планет, Кеплер вынужден был признавать, что их реальное поведение не вписывается в очерченные им стройные рамки. По меткому замечанию современного британского биолога Джона Холдейна, «идея Вселенной как геометрически совершенного произведения искусства оказалась ещё одной прекрасной гипотезой, разрушенной уродливыми фактами».

Лишь переехав в Прагу и став учеником датского астронома Тихо Браге, Кеплер натолкнулся на идеи, по-настоящему обессмертившие его имя в анналах науки.

Представим себе проблему, с которой столкнулся Кеплер, следующим образом. Мы находимся на планете, которая, во-первых, вращается вокруг своей оси, а во-вторых, обращается вокруг Солнца по неизвестной нам орбите. Глядя в небо, мы видим другие планеты, которые также движутся по неизвестным нам орбитам. Вопрос: как по данным наблюдений, сделанных на одном вращающемся вокруг оси и вокруг Солнца шарике, определить орбиту и скорость движения других планет?

Кажется, что вопрос достаточно сложный, даже при современном уровне компьютеров. А у Кеплера их не было и, тем не менее, ему удалось найти ответ!

Наблюдая за движением Марса в пространстве, а также воспользовавшись многолетними определениями координат и конфигураций этой планеты, проведёнными Тихо Браге, Кеплер обратил внимание на то, что Марс движется неравномерно. Он решил построить орбиту Марса. Для этого он сделал небольшое приближение, посчитав орбиту Земли круговой (что не противоречило наблюдениям). Затем он рассуждал примерно так. Пусть нам известно угловое расстояние Марса (точка М на рисунке) от точки весеннего равноденствия во время одного из противостояний планеты, то есть его прямое восхождение α

1.

Т₁ — это положение Земли во время противостояния с Марсом.

Для того, чтобы Марс оказался вновь в этой же точке своей орбиты, должно пройти 687 суток (таков звёздный период обращения Марса). Сидерический же период Земли равен 365 суткам. Поэтому, она не успеет «добежать» до точки T₁ и в этот момент будет находиться на своей орбите в точке Т₂. Следовательно, для наблюдателя измениться прямое восхождение Марса. Так вот раз за разом изучая различные противостояния Марса Кеплер получил целый ряд точек. Соединив их плавной кривой, он построил орбиту этой планеты, которая, как оказалось, не являлась окружностью.

Теперь Кеплер был поставлен перед необходимостью сделать выбор одного из двух возможных решений: считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями; или же считать, что все наблюдения были правильными, а орбита планеты действительно не является окружностью. Будучи уверенным в точности своих наблюдений и наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется

эллипсом. При этом Солнце располагается не в его центре. В результате им был сформулирован закон, который впоследствии назвали первым законом Кеплера: все планеты обращаются по эллипсам, в одном из фокусов которых находится Солнце.

На рисунке точка О — это центр эллипса, а F₁ и F₂ — его фокусы.

Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется его

большой осью.

А отрезок, проходящий через центр эллипса перпендикулярно большой оси, называется малой осью эллипса.

Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях, называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются малыми буквами a и b.

Отличие эллипса от окружности характеризуется величиной его эксцентриситета. Он равен половине отношения фокусного расстояния эллипса к его большой полуоси:

Отметим, что в случае, когда эксцентриситет эллипса равен нулю, фокусы и центр эллипса сливаются в одну точку — эллипс превращается в окружность.

Теперь предположим, что Солнце расположено в фокусе F₁. Тогда ближайшая к Солнцу точка орбиты планеты называется перигелием. А наиболее удалённая от Солнца точка, называется

афелием.

Например, у земной орбиты эксцентриситет равен 0,017, то есть орбита действительно почти круговая. В перигелии наша планета находится в начале января. Расстояние до Солнца составляет около 147 миллионов километров. Афелий Земля проходит в начале июля, а афелийное расстояние составляет чуть более 152 миллионов километров.

Но вернёмся к Кеплеру и построенной им траектории Марса. Изучив расположения полученных точек, он увидел, что скорость Марса по орбите меняется. Но при этом радиус-вектор планеты (то есть линия, соединяющая центр Солнца с центром планеты) за равные промежутки времени описывает равновеликие площади.

Обнаруженная закономерность впоследствии получила название второго закона Кеплера (иногда его называют законом площадей).

Чтобы лучше понять его физический смысл, вспомните своё детство. Наверняка, вам доводилось на детской площадке раскручиваться вокруг столба, ухватившись за него руками.

Фактически, планеты обращаются вокруг Солнца аналогичным образом. Чем дальше от Солнца уводит планету эллиптическая орбита, тем медленнее движение, чем ближе к Солнцу — тем быстрее движется планета.

Объяснить данный закон можно на основе закона сохранения энергии. Из физики вам известно, что полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остаётся неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна в каждой точке орбиты планеты. Приближаясь к Солнцу потенциальная энергия планеты уменьшается, в следствии уменьшения расстояния до Солнца. Поэтому её кинетическая энергия должна увеличиваться. А сделать это можно лишь за счёт увеличения скорости.

Таким образом, скорость движения планеты по орбите меняется, принимая максимальное значение в перигелии и минимальное в афелии.

Первый и второй законы были опубликованы Кеплером в 1609 году в книге «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс.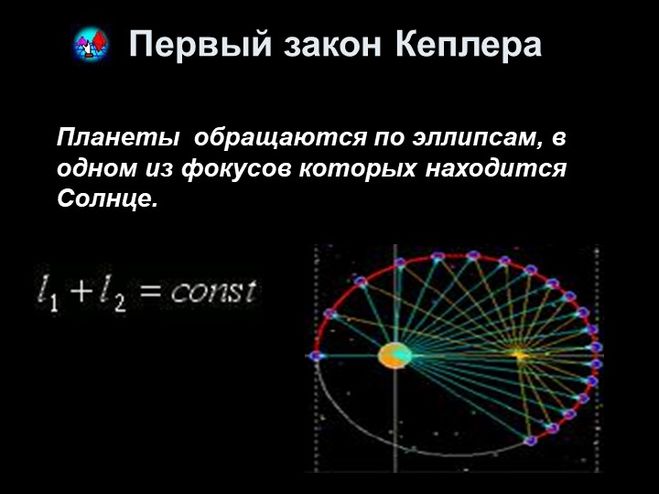 ..». Хотя реально первый закон Кеплера был открыт в тысяча шестьсот пятом 1605 году, а второй — тысяча шестьсот втором 1602.

Свой третий закон Кеплер сформулировал лишь в 1618 году. Он гласит, что квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит:

Вот что писал по этому поводу сам Кеплер: «То, что 16 лет тому назад я решил искать, <…> наконец найдено, и это открытие превзошло все мои самые смелые ожидания…».

И действительно, третий закон заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя уже известные их периоды обращения вокруг него. При этом не нужно вычислять расстояния от Солнца до каждой планеты, достаточно измерить это расстояние для одной из них, например, Земли. Кстати, для простоты вычислений, величину большой полуоси́ орбиты Земли приняли равной одной астрономической единице (1 а. е.). Эта единица измерения стала основой для вычисления всех остальных расстояний в Солнечной системе.

Ещё раз обратим ваше внимание на то, что Кеплер открыл свои законы исходя только из собственных наблюдений, и наблюдений Тихо Браге. Если бы вы спросили его, чем обусловлена эллиптичность орбит или равенство площадей секторов, он бы вам не ответил. Это просто следовало из проведённого им анализа. Если бы вы спросили его об орбитальном движении планет в других звёздных системах, он также не нашёл бы ответа на этот вопрос.

Однако гений Кеплера в том и заключался, что он смог увидеть то, во что остальные отказывались верить. А строгое математическое доказательство его законы получили лишь после того, как Ньютоном были открыты закон Всемирного тяготения и закон сохранения момента импульса (известный нам второй закон Ньютона). Но об этом в следующий раз. А сейчас давайте решим с вами одну небольшую задачку. Определите период обращения астероида Россия, если большая полуось его орбиты равна 2,55 а. е.

Закон Кеплера — формулировка законов, рисунки и примеры

Покажем, как применять знание физики в жизни

Начать учиться

«Сижу, никого не трогаю, решаю задания из ЕГЭ, а тут в решении астрономического 24‑го какие-то законы Кеплера. Ничего не понятно, но очень интересно», — так думают многие одиннадцатиклассники, сдающие физику. Рассказываем, как понять эти законы и использовать в решении задачек.

Форма Земли

Сейчас нам сложно представить, что раньше люди верили, будто Земля плоская. У греков, например, плоскость просто парила в воздухе и была окружена ледниками. А в Индии верили, что планета покоится на трех слонах, которые стоят на черепахе. Впрочем, кое-кто до сих пор так думает. Доказательств того, что наша планета на самом деле не плоская — много, но вот вам парочка, чтобы можно было поддержать светскую беседу.

Смена дня и ночи

По представлениям приверженцев плоской Земли, день и ночь сменяются, потому что Луна и Солнце вращаются над Землей — вот как-то так:

Но — упс! — эта модель вызывает целый ряд вопросов:

• Почему длина дня и ночи меняется в течение года?

• Чем объясняется цвет заката и восхода?

• Почему иногда мы можем увидеть Луну и Солнце одновременно?

• Почему Луна и Солнце не появляются каждый раз из одной и той же точки?

• Если нет гравитационного притяжения, почему они вообще крутятся?

Лунные затмения

Если Земля плоская, то непонятно, как объяснить лунные затмения. Чтобы затмение произошло, нужно, чтобы Солнце находилось по одну сторону от диска, а Луна — по другую. Тогда ломается концепция дня и ночи, которую мы описали выше, ведь день и ночь будут наступать для всей Земли одновременно.

Тени

На плоскую Землю свет от Солнца падал бы, как свет от фонаря. То есть высокие объекты в противоположном от Солнца направлении после заката оставались бы в тени.

А на шарообразной Земле небоскребы или горы будут освещены Солнцем после заката или перед рассветом.

Именно это вы увидите, если застанете рассвет или закат в горах — или посмотрите на фотографии.

Окей, Земля все-таки не плоская — с этим разобрались. Но и шаром ее назвать нельзя: Земля имеет форму эллипсоида.

Эллипсоид — это такой приплюснутый шар, в одном из сечений у которого эллипс. Именно по траектории эллипса вращаются все спутники.

Пятерка по физике у тебя в кармане!

Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!

Эллипс

Эллипс — это замкнутая прямая на плоскости, частный случай овала. У эллипса две оси симметрии — горизонтальная и вертикальная, которые состоят из двух полуосей.

А еще у эллипса два фокуса — это такие точки, сумма расстояний от которых до любой точки P(x,y) является постоянной величиной.

Эллипс F1 и F2 — фокусы F1 = ( c ; 0) F2 = (-c ; 0) с — половина расстояния между F1 и F2 a — большая полуось b — малая полуось r1 и r2 — фокальные радиусы

Теперь мы знаем все необходимые понятия, чтобы разобраться, в чем состоят законы Кеплера.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Первый закон Кеплера

Каждая планета солнечной системы вращается вокруг Солнца по эллипсоидной орбите, в одном из фокусов которого находится Солнце.

Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка B траектории называется перигелием, а точка A, наиболее удаленная от Солнца — афелием.

Первый закон Кеплера достаточно простой, но важный, так как в свое время он сильно продвинул астрономию. До этого открытия астрономы считали, что планеты движутся исключительно по круговым орбитам. Если же наблюдения противоречили этому убеждению, ученые дополняли главное круговое движение малыми кругами, которые планеты описывали вокруг точек основной круговой орбиты. Кеплер получил доступ к огромной базе наблюдений Тихо Браге и, изучив их, перешагнул старые идеи.

Второй закон Кеплера (закон площадей)

Радиус-вектор, соединяющий планету и Солнце, описывает в равные промежутки времени равные площади.

Каждая планета перемещается в плоскости, проходящей через центр Солнца. За равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Таким образом, тела движутся вокруг Солнца неравномерно: в перигелии они имеют максимальную скорость, а в афелии — минимальную.

На практике это можно заметить по движению Земли. Ежегодно в начале января наша планета проходит через перигелий и перемещается быстрее. Из-за этого движение Солнца по эклиптике (линии, показывающей путь Солнца по небу) также происходит быстрее, чем в другое время года. В начале июля Земля движется через афелий, из-за чего Солнце по эклиптике перемещается медленнее. Поэтому световой день летом длиннее, чем зимой.

Третий закон Кеплера

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Согласно третьему закону Кеплера, между периодом обращения планет вокруг Солнца и большими полуосями их орбит устанавливается связь. Этот закон выполняется как для планет, так и для спутников с погрешно­стью менее 1%.

Третий закон Кеплера T1 и T2 — периоды обращения двух планет [c] a1 и a2 — большие полуоси орбит планет [м]

На основании этого закона можно вычис­лить продолжительность года (времени полного оборота вокруг Солнца) любой планеты, если известно ее расстояние до Солнца в афелии.

Также можно проделать обратное — рассчитать орбиту, зная период обращения.

Закон всемирного тяготения

Законы Кеплера — это результаты наблюдений и обобщений. Впоследствии они легли в основу закона всемирного тяготения, который звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2

Ньютон был первым исследователем, который пришел к выводу, что между любыми телами в космосе действуют гравитационные силы, и именно они определяют характер движения этих тел.

Первая и вторая космические скорости

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Чтобы промахнуться мимо Земли и стать ее искусственным спутником, нужно достичь первой космической скорости 7,9 км/с. Вот как это происходит:

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него это получалось, аппарат должен иметь начальную скорость, которая равна или больше первой космической.

Первая космическая скорость v1 — первая космическая скорость [м/с] g — ускорение свободного падения на данной планете [м/с2] R — радиус планеты [м] На планете Земля g ≈ 10 м/с2.

Есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Вторая космическая скорость v2 — вторая космическая скорость [м/с] g — ускорение свободного падения на данной планете [м/с2] R — радиус планеты [м] На планете Земля g ≈ 10 м/с2.

Карина Хачатурян

К предыдущей статье

Скорость света

К следующей статье

Явление самоиндукции

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

законов движения планет Кеплера | Определение, диаграммы и факты

Первый закон Кеплера

Смотреть все СМИ

Ключевые люди:

Иоганн Кеплер

Похожие темы:

небесная механика Второй закон Кеплера о движении планет Третий закон Кеплера движения планет Первый закон движения планет Кеплера

Просмотреть весь связанный контент →

Популярные вопросы

Что означает первый закон Кеплера?

Первый закон Кеплера означает, что планеты движутся вокруг Солнца по эллиптическим орбитам. Эллипс – это фигура, напоминающая сплющенный круг. Насколько сплющен круг, выражается его эксцентриситетом. Эксцентриситет — это число от 0 до 1. Для идеального круга он равен нулю.

орбита

Подробнее об орбите планеты.

Что такое эксцентриситет и как он определяется?

Эксцентриситет эллипса измеряет, насколько он сплющен в окружности. Он равен квадратному корню из [1 — b*b/(a*a)]. Буква a обозначает большую полуось, ½ расстояния поперек длинной оси эллипса. Буква b обозначает малую полуось, ½ расстояния поперек короткой оси эллипса. Для идеального круга a и b одинаковы, так что эксцентриситет равен нулю. Орбита Земли имеет эксцентриситет 0,0167, так что это почти идеальный круг.

эллипс

Подробнее об эллипсах.

Что означает третий закон Кеплера?

Время, необходимое планете для обращения вокруг Солнца (период P), зависит от среднего расстояния планеты от Солнца (d). То есть квадрат периода P*P, деленный на куб среднего расстояния d*d*d, равен константе. Для каждой планеты, независимо от ее периода или расстояния, P*P/(d*d*d) — одно и то же число.

небесная механика: приближенный характер законов Кеплера

Узнайте больше о приближенном характере третьего закона Кеплера.

Почему орбита планеты тем медленнее, чем дальше она от Солнца?

Планета движется медленнее, чем дальше от Солнца, потому что ее угловой момент не меняется. Для круговой орбиты угловой момент равен массе планеты (m), умноженной на расстояние планеты от Солнца (d), умноженное на скорость планеты (v). Поскольку m*v*d не меняется, когда планета находится близко к Солнцу, d становится меньше, когда v становится больше. Когда планета находится далеко от Солнца, d становится больше, а v становится меньше.

принципы физических наук: законы сохранения и экстремальные принципы

Подробнее о сохранении углового момента.

Где находится Земля, когда она движется быстрее всего?

Из второго закона Кеплера следует, что Земля движется быстрее всего, когда находится ближе всего к Солнцу.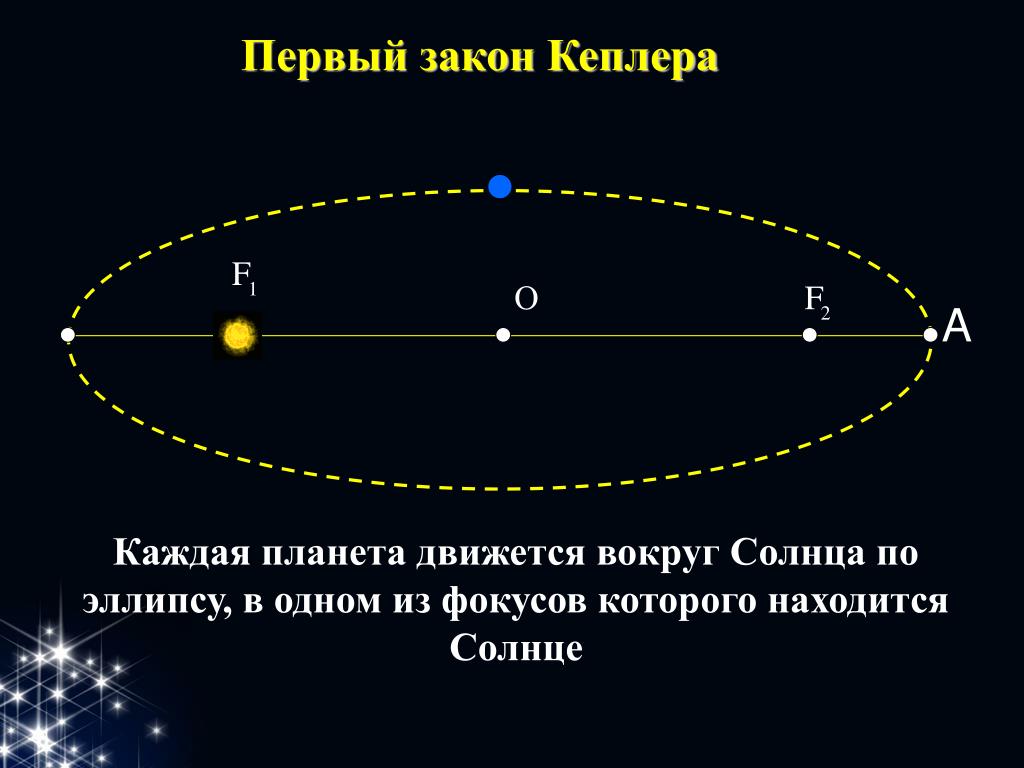 Это происходит в начале января, когда Земля находится на расстоянии около 147 миллионов километров (91 миллион миль) от Солнца. Когда Земля находится ближе всего к Солнцу, она движется со скоростью 30,3 километра (18,8 мили) в секунду.

Узнайте, как законы Кеплера анализируют эллипсы, эксцентриситет и угловой момент как часть физики Солнечной системы

Просмотреть все видео к этой статье

Узнайте, как Иоганн Кеплер бросил вызов коперниковской системе движения планет Законы Кеплера о движении планет , в астрономии и классической физике, законы, описывающие движение планет в Солнечной системе. Они были выведены немецким астрономом Иоганном Кеплером, чей анализ наблюдений датского астронома XVI века Тихо Браге позволил ему объявить свои первые два закона в 1609 году.и третий закон почти десять лет спустя, в 1618 году. Сам Кеплер никогда не нумеровал эти законы и не отличал их особо от других своих открытий.

Три закона движения планет Кеплера можно сформулировать следующим образом: (1) Все планеты движутся вокруг Солнца по эллиптическим орбитам, имея Солнце в качестве одного из фокусов. (2) Радиус-вектор, соединяющий любую планету с Солнцем, заметает равные площади за равные промежутки времени. (3) Квадраты сидерических периодов (обращения) планет прямо пропорциональны кубам их средних расстояний от Солнца. Знание этих законов, особенно второго (закона площадей), оказалось решающим для сэра Исаака Ньютона в 1684–1685 годах, когда он сформулировал постулированный им знаменитый закон тяготения между Землей и Луной и между Солнцем и планетами. чтобы иметь силу для всех объектов в любой точке Вселенной. Ньютон показал, что движение тел, подверженных центральной гравитационной силе, не всегда должно следовать по эллиптическим орбитам, указанным в первом законе Кеплера, но может двигаться по путям, определяемым другими, открытыми коническими кривыми; движение может быть по параболическим или гиперболическим орбитам, в зависимости от полной энергии тела. Таким образом, объект достаточной энергии — например, комета — может войти в Солнечную систему и снова уйти, не возвращаясь. Из второго закона Кеплера можно далее заметить, что угловой момент любой планеты относительно оси, проходящей через Солнце и перпендикулярной плоскости орбиты, также неизменен.

Викторина «Британника»

Викторина «Наука»

планетарные орбиты: Кеплер, Ньютон и гравитация

Посмотреть все видео к этой статье

Полезность законов Кеплера распространяется на движение естественных и искусственных спутников, а также на звездные системы и внесолнечные планеты. Законы, сформулированные Кеплером, конечно, не учитывают гравитационные взаимодействия (как возмущающие воздействия) различных планет друг на друга. Общая задача точного предсказания движения более чем двух тел под их взаимным притяжением весьма сложна; аналитические решения задачи трех тел недостижимы, за исключением некоторых частных случаев. Можно отметить, что законы Кеплера применимы не только к гравитационным, но и ко всем другим силам обратных квадратов, а также, если должным образом учитывать релятивистские и квантовые эффекты, к электромагнитным силам внутри атома.

Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена ​​Барбарой А. Шрайбер.

Три закона Кеплера

В начале 1600-х годов Иоганн Кеплер предложил три закона движения планет. Кеплер смог обобщить тщательно собранные данные своего наставника Тихо Браге тремя утверждениями, описывающими движение планет в солнечной системе с центром в центре Солнца. Попытки Кеплера объяснить основные причины таких движений больше не принимаются; тем не менее, сами фактические законы по-прежнему считаются точным описанием движения любой планеты и любого спутника.

Три закона движения планет Кеплера можно описать следующим образом:

• Путь планет вокруг Солнца имеет эллиптическую форму, при этом центр Солнца находится в одном фокусе. (Закон эллипсов)
• Воображаемая линия, проведенная от центра Солнца к центру планеты, заметает равные площади за равные промежутки времени. (Закон равных площадей)
• Отношение квадратов периодов любых двух планет равно отношению кубов их средних расстояний от Солнца. (Закон Гармоний)

Закон эллипсов

Первый закон Кеплера, иногда называемый законом эллипсов, объясняет, что планеты вращаются вокруг Солнца по траектории, описываемой как эллипс. Эллипс можно легко построить с помощью карандаша, двух кнопок, веревки, листа бумаги и куска картона. Прикрепите лист бумаги к картону двумя кнопками. Затем завяжите нить в петлю и оберните петлю вокруг двух кнопок. Возьмите карандаш и тяните за нитку, пока карандаш и две кнопки не образуют треугольник (см. рисунок справа). Затем начните обводить путь карандашом, плотно обмотав нитку вокруг кнопок. В результате получится эллипс. Эллипс — это особая кривая, в которой сумма расстояний от каждой точки кривой до двух других точек является постоянной величиной. Две другие точки (обозначенные здесь положениями галса) известны как 9-я точка.0065 фокусов эллипса. Чем ближе друг к другу эти точки, тем больше эллипс напоминает форму круга. На самом деле круг — это частный случай эллипса, в котором два фокуса находятся в одном месте. Первый закон Кеплера довольно прост: все планеты вращаются вокруг Солнца по траектории, напоминающей эллипс, причем Солнце находится в одном из фокусов этого эллипса.

Закон равных площадей

Второй закон Кеплера, иногда называемый законом равных площадей, описывает скорость, с которой любая планета будет двигаться по орбите вокруг Солнца. Скорость, с которой любая планета движется в космосе, постоянно меняется. Планета движется быстрее всего, когда она находится ближе всего к Солнцу, и медленнее всего, когда она дальше всего от него. Однако если воображаемую линию провести от центра планеты к центру Солнца, то эта линия охватит ту же площадь за равные промежутки времени. Например, если воображаемую линию провести от земли к солнцу, то площадь, заметаемая этой линией за каждый 31-дневный месяц, будет одинаковой. Это изображено на диаграмме ниже. Как видно на диаграмме, области, образованные, когда Земля находится ближе всего к Солнцу, можно аппроксимировать широким, но коротким треугольником; тогда как области, образованные, когда Земля находится дальше всего от Солнца, могут быть аппроксимированы узким, но длинным треугольником. Эти области имеют одинаковый размер. С с основанием этих треугольников являются самыми короткими, когда Земля находится дальше всего от Солнца, Земля должна двигаться медленнее, чтобы эта воображаемая площадь была того же размера, что и когда Земля находится ближе всего к Солнцу.

 

Закон гармоний

Третий закон Кеплера, иногда называемый законом гармоний , сравнивает период обращения и радиус орбиты планеты с таковыми у других планет. В отличие от первого и второго законов Кеплера, описывающих характеристики движения одной планеты, третий закон сравнивает характеристики движения разных планет. Проводится сравнение, заключающееся в том, что отношение квадратов периодов к кубам их средних расстояний от Солнца одинаково для каждой из планет. В качестве иллюстрации рассмотрим период обращения и среднее расстояние от Солнца (радиус орбиты) для Земли и Марса, как указано в таблице ниже.

Планета	Период (с)	Среднее Расстояние (м)	T 2 /R 3 (s 2 /m 3 )
Земля	3,156 x 10 7 с	1,4957 x 10 11	2,977 x 10 -19
Марс	5,93 x 10 7 с	2,278 x 10 11	2,975 x 10 -19

 

Обратите внимание, что соотношение T ² /R ³ для Земли такое же, как и для Марса. На самом деле, если такое же отношение T ² /R ³ вычислить для других планет, можно обнаружить, что это отношение является почти одинаковым значением для всех планет (см. таблицу ниже). Удивительно, но на каждой планете одинаковый T ^{2 9Соотношение 0159/R 3 .}

Планета	Период (год)	Среднее Расстояние (а.е.)	T 2 /R 3 (год 2 /au 3 )
Меркурий	0,241	0,39	0,98
Венера	. 615	0,72	1.01
Земля	1,00	1,00	1,00
Марс	1,88	1,52	1.01
Юпитер	11,8	5,20	0,99
Сатурн	29,5	9,54	1,00
Уран	84,0	19.18	1,00
Нептун	165	30. 06	1,00
Плутон	248	39,44	1,00

( ПРИМЕЧАНИЕ : Среднее значение расстояния дано в астрономических единицах, где 1 а. 1 земной год — это время, необходимое Земле для обращения вокруг Солнца — 3,156 х 10 ⁷ секунд. )

 

Третий закон Кеплера дает точное описание периода и расстояния по орбите планеты вокруг Солнца. Кроме того, тот же закон, который описывает отношение T ² /R ³ для орбит планет вокруг Солнца, также точно описывает отношение T ² /R ³ для любого спутника (будь то луна или человек). спутник) о любой планете. В этом Т 9 есть что-то гораздо более глубокое.0158 2 /R ³ отношение — то, что должно относиться к основным фундаментальным принципам движения. В следующей части Урока 4 эти принципы будут исследованы по мере того, как мы будем проводить связь между принципами кругового движения, обсуждавшимися в Уроке 1, и движением спутника.

Как Ньютон расширил свое понятие гравитации, чтобы объяснить движение планет?

Сравнение Ньютоном ускорения Луны с ускорением объектов на Земле позволило ему установить, что Луна удерживается на круговой орбите силой тяжести — силой, которая находится в обратной зависимости от расстояния между центрами двух объектов. . Установление гравитации как причины орбиты Луны не обязательно означает, что гравитация является причиной орбит планеты. Как же тогда Ньютон представил достоверные доказательства того, что сила гравитации соответствует требованию центростремительной силы для эллиптического движения планет?

Напомним, что ранее в Уроке 3 Иоганн Кеплер предложил три закона движения планет. Его закон гармонии предполагал, что отношение квадрата периода обращения ( T ² ) к среднему радиусу обращения в кубе ( R ³ ) равно одному и тому же значению k для всех планет, обращающихся по орбите. солнце. Известные данные для вращающихся планет предполагают следующее среднее соотношение:

к = 2,97 х 10 ^-19  с ² /м ³  = (T ² )/(R ³ )

Ньютон смог объединить закон всемирного тяготения с принципами кругового движения, чтобы показать, что если сила тяжести обеспечивает центростремительную силу для почти круговых орбит планет, то значение 2,97 x 10 ^-19  с ² /m ³ можно было предсказать для отношения T ² /R ³ . Вот рассуждения, используемые Ньютоном:

Рассмотрим планету с массой M _{планету}  , совершающую почти круговое движение вокруг Солнца с массой M _Солнце . Суммарная центростремительная сила, действующая на эту вращающуюся вокруг планеты, определяется соотношением

F _сеть  = (M _{планета}  * v ² ) / R

Эта результирующая центростремительная сила является результатом гравитационной силы, которая притягивает планету к Солнцу, и может быть представлена ​​как

F _грав  = (G* M _{планета} * M _Солнце ) / R ²

Поскольку F _grav  = F _net , приведенные выше выражения для центростремительной силы и силы тяжести равны. Таким образом,

(M _{планета}  * v ² ) / R = (G* M _{планета}  * M _Солнце  ) / R ²

Так как скорость объекта на почти круговой орбите может быть аппроксимирована как v = (2*pi*R) / T,

v ²  = (4 * pi ²  * R ² ) / T ²

Подстановка выражения для v ²  в приведенное выше уравнение дает

(M _{планета}  * 4 * pi ²  * R ² ) / (R • T ² ) = (G* M _{планета} * M _Солнце ) / R ²

Путем перекрестного умножения и упрощения уравнение можно преобразовать в

T ²  / R ³  = (M _{планета}  * 4 * пи ² ) / (G* M _{планета}  * M _Солнце  )

Затем массу планеты можно вычесть из числителя и знаменателя правой части уравнения, что даст

T ² / R ³ = (4 * pi ² ) / (G * M _Sun )

Правая часть приведенного выше уравнения будет одинаковой для каждой планеты независимо от массы планеты. Следовательно, разумно, что отношение T ² /R ³ будет одинаковым для всех планет, если сила, которая удерживает планеты на их орбитах, является силой гравитации. Универсальный закон всемирного тяготения Ньютона предсказывает результаты, которые согласуются с известными планетарными данными и обеспечивают теоретическое объяснение закона гармонии Кеплера.

 

Расследуй!

Ученые знают о планетах гораздо больше, чем во времена Кеплера. Используйте виджет The Planets , чтобы узнать, что известно о различных планетах.

 

Проверьте свое понимание

1. Наше понимание эллиптического движения планет вокруг Солнца продолжалось несколько лет и включало вклад многих ученых.

а. Какому ученому приписывают сбор данных, необходимых для поддержки эллиптического движения планеты?

б. Какому ученому приписывают долгую и сложную задачу анализа данных?

в. Какому ученому приписывают точное объяснение данных?

 

2. Галилею часто приписывают раннее открытие четырех из множества спутников Юпитера. Луны, вращающиеся вокруг Юпитера, следуют тем же законам движения, что и планеты, вращающиеся вокруг Солнца. Один из спутников называется Ио — его расстояние от центра Юпитера составляет 4,2 единиц и обращается вокруг Юпитера за 1,8 земных дня. Другая луна называется Ганимед; это 10,7 единицы от центра Юпитера. Сделайте предсказание периода Ганимеда, используя закон гармоний Кеплера.

 

3. Предположим, открыта маленькая планета, которая находится в 14 раз дальше от Солнца, чем Земля от Солнца (1,5 х 10 ¹¹ м). Используйте закон гармоний Кеплера, чтобы предсказать период обращения такой планеты. ДАННО: Т ² /R ³ = 2,97 x 10 ^-19 с ² /м ³

 

4. Среднее орбитальное расстояние Марса в 1,52 раза больше среднего орбитального расстояния Земли. Зная, что Земля совершает оборот вокруг Солнца примерно за 365 дней, используйте закон гармоний Кеплера, чтобы предсказать время обращения Марса вокруг Солнца.

 

Данные о радиусе и периоде обращения четырех крупнейших спутников Юпитера приведены в таблице ниже. Масса планеты Юпитер 1,9.х 10 ²⁷ кг. Основывайте свои ответы на следующие пять вопросов на этой информации.

Луна Юпитера	Период(ы)	Радиус (м)	Т 2 /Р 3
Ио	1,53 x 10 5	4,2 x 10 8	а.
Европа	3,07 x 10 5	6,7 x 10 8	б.
Ганимед	6,18 x 10 5	1,1 x 10 9	в.
Каллисто	1,44 x 10 6	1,9 х 10 9	д.

5. Определите отношение T ² /R ³ (последний столбец) для спутников Юпитера.

 

6. Какую закономерность вы наблюдаете в последнем столбце данных? Какой закон Кеплера это подтверждает?

 

7.