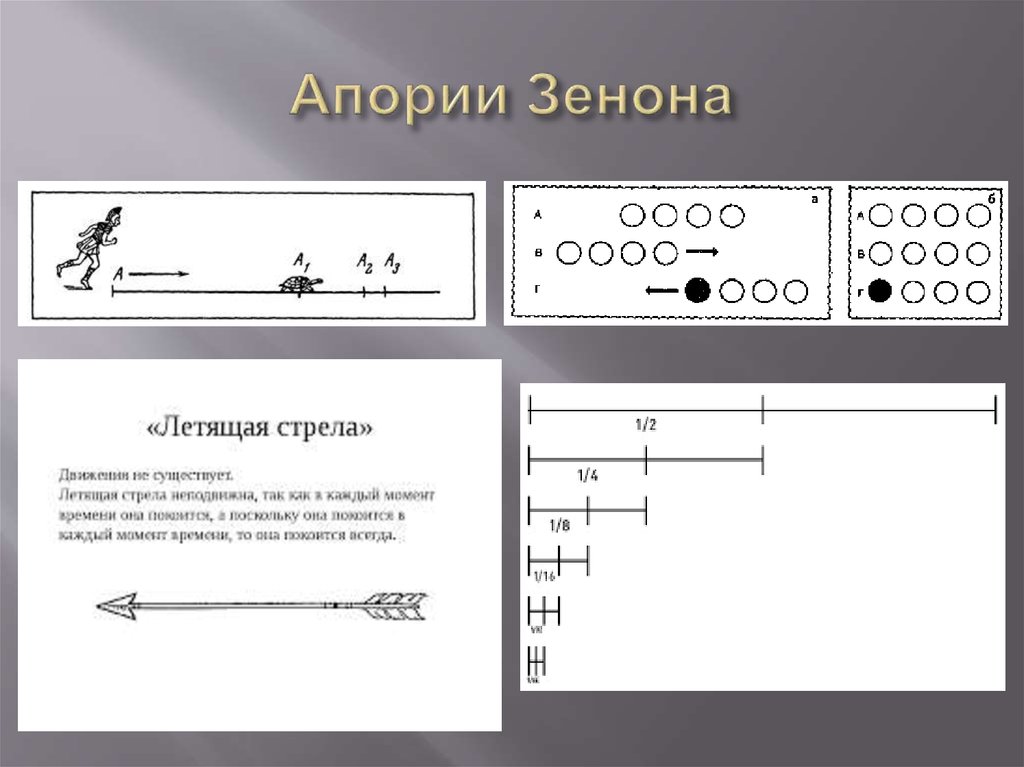
Апории Зенона — Wikiwand

• ВведениеАпории Зенона
• Философия элеатов
• Апории о движенииМодели движения в античной натурфилософииСодержание апорий о движенииАхиллес и черепахаДихотомияЛетящая стрелаКритика апорий АристотелемАтомистический подходОбсуждение в Новое времяСовременная трактовкаАдекватность аналитической теории движения
• Другие апории ЗенонаСтадионМножественностьМераО местеМедимн зерна
• Историческое значение апорий Зенона
• Апории Зенона в литературе и искусстве
• См. также
• Примечания
• Литература
• Ссылки

Апори́и Зено́на (от др.-греч. ἀπορία «трудность») — внешне парадоксальные рассуждения на тему о движении и множестве древнегреческого философа Зенона Элейского (V век до н. э.).

Зенон Элейский
книжная гравюра XVII века

Современники упоминали более 40 апорий Зенона, до нас дошли 9, обсуждаемые в «Физике» и в других трудах Аристотеля, а также в комментариях Симпликия, Филопона и Фемистия к Аристотелю[1]; одна апория из этих 9 приводится также у Диогена Лаэртского[2], апории о множестве обсуждаются в диалоге Платона «Парменид».

Комментатор Аристотеля Элий Александрийский (VI век) сообщает, что Зенон высказал 40 рассуждений (эпихейрем) о множестве и пять — о движении[3]:

Он составил для своего учителя Парменида, который утверждал, что сущее одно по виду, но множественно согласно очевидности, {аргументацию} из сорока эпихейрем в пользу того, что сущее одно, так как считал, что быть союзником учителя — это хорошо. Ещё как-то, защищая того же учителя, утверждавшего, что сущее неподвижно, он выдвинул пять эпихейрем в пользу того, что сущее неподвижно. Антисфен-киник, который не смог на них возразить, встал и стал ходить, полагая, что доказательство делом сильнее всякого возражения словом.

Наиболее известны парадокс «Ахиллес и черепаха» и другие апории Зенона о движении, которые обсуждаются более двух тысячелетий, им посвящены сотни исследований. Платон в «Пармениде» их не упоминает, поэтому В. Я. Комарова предполагает, что парадоксы движения были написаны Зеноном позднее других[4].

Ошибочно воспринимать эти рассуждения как софизмы или полагать, что с появлением высшей математики все апории разрешены[5]. Бертран Рассел писал, что апории Зенона «в той или иной форме затрагивают основания почти всех теорий пространства, времени и бесконечности, предлагавшихся с его времени до наших дней»[6]. «Проблематика аргументов Зенона далеко выходит за пределы конкретной исторической ситуации, обусловившей их появление. Анализу апорий Зенона посвящена колоссальная литература; особенно большое внимание им уделялось в последние сто лет, когда математики стали усматривать в них предвосхищение парадоксов современной теории множеств»[7]. Научные дискуссии, вызванные рассуждениями Зенона, существенно углубили понимание таких фундаментальных понятий, как роль непрерывного и дискретного (прерывного) в природе, адекватность физического движения и его математической модели и др. Эти дискуссии продолжаются и в настоящее время (см. список литературы), прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось[8].

2.2.3. Апория «Стадий» («Стадион»).

2.2.3.1. Формулировка апории.

Пусть по стадиону движутся по параллельным прямым равные массы с равной скоростью, но в противоположных направлениях. Пусть ряд А₁, А₂, А₃, А₄ означает неподвижные массы. Ряд В₁, В₂, В₃, В₄ означает массы, движущиеся вправо, а ряд Г₁, Г

2, Г₃, Г₄ означает массы, движущиеся влево.

Будем теперь рассматривать массы А_i, В_i, Г_i , как неделимые. В неделимый момент времени В_i и Г_i проходят неделимую часть пространства. Действительно, если бы в неделимый момент времени некоторое тело проходило более одной неделимой части пространства, то неделимый момент времени был бы делим, если же меньше, то можно было бы разделить неделимую часть пространства. Рассмотрим теперь движение неделимых В_i и Г_i друг относительно друга: за два неделимых момента времени В₄ пройдет две неделимые части А_i и одновременно отсчитает четыре неделимых части Г_i , то есть неделимый момент окажется делимым.

Этой апории можно придать и несколько другую форму. За одно и то же время t точка В₄ проходит половину пути отрезка А

1А₄ и целый отрезок Г₁Г₄ . Но каждому неделимому моменту времени отвечает неделимая часть пространства, проходимая за это время. Тогда в некотором отрезке α и 2α содержится «одинаковое» число точек, «одинаковое» в том смысле, что между точками обоих отрезков можно установить взаимно однозначное соответствие. Этим впервые было установлено такое соответствие между точками отрезков различной длины. Если считать, что мера отрезка получается как сумма мер неделимых, то вывод является парадоксальным.

2.2.3.2. Логическая ошибка в основе апории «Стадий»

скрывается за неявно выраженным нарушением логических законов построения мыслей. Это нарушение состоит в подспудном признании взаимной относительности движения тел А₁ и А₂, поскольку в апории все же идет речь о движении тела А₁ относительно тела А₂(или наоборот), при одновременном явном отрицании этой относительности, так как игнорируется такой параметр этого движения, как скорость ω реляционного движения, равная сумме модулей скоростей υ

1 и -υ₂ движений тел А₁ и А₂ по отношению к телу А₀. В явном виде логически противоречивая структура данной апории может быть представлена формулой х ( P(x)  P(x) ), где лишь исключающие друг друга пропозициональные функции означают одновременно признание и отрицание предикатов относительности и реальности реляционного движения тел А₁ и А₂.

2.2.4. «Ахиллес и черепаха».

2.2.4.1. Суть апории.

Быстроногий Ахиллес никогда не догонит черепаху, если в начале движения черепаха находилась на некотором расстоянии впереди него. Действительно, пусть начальное расстояние есть α и пусть Ахиллес бежит в k раз быстрее черепахи. Когда Ахиллес пройдет расстояние α, черепаха отползет на α/k, когда Ахиллес пройдет это расстояние, черепаха отползет на α/k², и так далее, то есть всякий раз между состязающимися будет оставаться отличное от нуля расстояние.

2.2.4.2. Противоречивость апории.

В этой апории, помимо того же затруднения отсчитанной бесконечности, имеется и еще одно. Предположим, что в некоторый момент времени t_ω Ахиллес догонит черепаху.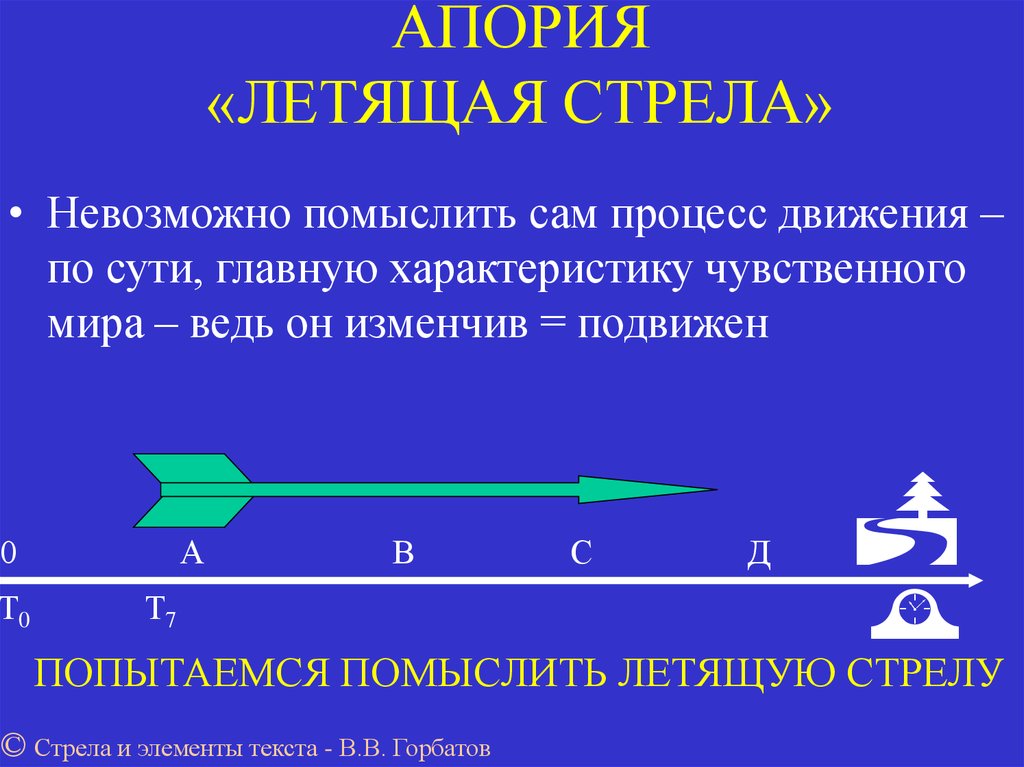 Запишем путь Ахиллеса

S_A=

и путь черепахи

S_A=

Каждому отрезку пути , пройденному Ахиллесом, соответствует отрезок путичерепахи. Поэтому к моменту встречи Ахиллес должен пройти «столько же» отрезков пути, сколько и черепаха. С другой стороны, каждому отрезку пути, пройденному черепахой, можно сопоставить равный ему по величине отрезок пути Ахиллеса. Но, кроме того, Ахиллес должен пробежать еще один отрезок длиныα, то есть он должен пройти на единицу больше отрезков, чем черепаха. Если количество отрезков, пройденное последней, есть α, то получаем

1+α= α.

Это последнее затруднение: «часть равна целому» — явилась впоследствии предметом размышления Галилея, Николая Кузанского и многих других, которые давали этому парадоксу различные интерпретации. Чешский ученый Б. Болцано в первой половине XIX века установил, что любое бесконечное множество может быть приведено во взаимно однозначное соответствие со своей правильной частью. Теперь это свойство иногда принимается в качестве определения бесконечного множества.

Зенон, как известно, не отрицавший реальности движения, не смог лишь логически последовательно осмыслить последнее, допуская трудно обнаружимое нарушение основных логических принципов. Констатируя этот факт, В.И. Ленин высказал свое замечание: «Вопрос не в том, есть ли движение, а как его выразить в логике понятий», чтобы избежать при этом формально логической непоследовательности. Задача эта вполне разрешима уже с помощью средств, которыми располагает современная символическая логика и которые позволяют логически непротиворечиво отобразить диалектическую противоречивость объективно реального процесса движения.

Avantgarde Museum

Дэвид Нез родился в 1949 году в штате Массачусетс, США. Окончил Академию изящных искусств в Любляне, Словения. Он присоединился к OHO в 1968 году, участвуя в выставках, мероприятиях, фотопроектах и ​​фильмах. Сначала он создавал объекты, затем среды и инсталляции. Среди « летних проектов » OHO выделяются его инсталляции зеркал, расположенных в ландшафте. Позже был создан ряд процессуальных работ, за которыми последовало несколько концептуальных проектов, касающихся отношений между временем и пространством. Его последняя выставка в Югославии состоялась в 1972 в Салоне Muzeja savremene umetnosti (Салон Музея современного искусства) в Белграде, где он представил работу, которая принесла ему диплом. С 1971 по 1972 год он был частью семьи Шемпас. Сейчас он живет и работает в Балтиморе, штат Мэриленд.

Образование

А.Т.Р. Арт-терапия, Университет Нью-Мексико, Альбукерке, Нью-Мексико, 1989.

M.F.A. Живопись, Королевская школа живописи на горе, Колледж искусств Мэрилендского института,
Балтимор, Мэриленд, 1983.

Б.Ф.А. Живопись, Академия изящных искусств, Любляна, Республика Словения, 1972 г. Искусство на краю Европы», Музей Кроллера-Мюллера, Оттерлоо, Нидерланды
2005 «Недавние картины», Галерея Augen, Портленд, штат Орегон,
2003 «Демагоги», Галерея Augen, Портленд, OR
2002 «Выставка преподавателей муниципального колледжа Монро» , Государственный университет Нью-Йорка, Брокпорт, Нью-Йорк
1999 г. «Новые работы», Галерея Фэрбенкс, Университет штата Орегон, Корваллис, Орегон
1999 г. «Avant Discard», Центр искусств Большого Рестона, Рестон, Вирджиния
1999 г. «Недавние картины и скульптура», Галерея Оген, Портленд, Орегон,
1998 г. Алхимические картины », Галерея Дэвидсона, Сиэтл, Вашингтон
1996« Новые работы », Галерея Огена, Портленд или
1994 г. «Новые работы», Галерея K, Вашингтон, округ Колумбия.
1994 г. «Групповая ретроспектива OHO», Moderna Galerija, Любляна, Республика Словения
1993 г. «Трое из Балтимора», Галерея Роджера Лапеля, Филадельфия, Пенсильвания
1993 г. «Small is Beautiful» , Галерея K, Вашингтон, округ Колумбия
1992 «Летняя групповая выставка», Галерея K, Вашингтон, округ Колумбия
1991 «Нейтральная земля», Artscape, Балтимор, Мэриленд
1990 «Городские видения», Галерея Антона, Вашингтон, округ Колумбия
1987 «Три Художники», Галерея Антона, Вашингтон, округ Колумбия
1986 «Новый талант», Галерея Антона, Вашингтон, округ Колумбия,
1986 «Раскрашенная скульптура», Галерея Роджера Лапеля, Филадельфия, Пенсильвания,
1986 «Летняя скульптура», Галерея Роджера Лапеля, Филадельфия, Пенсильвания, Искусство, Балтимор, Мэриленд
1985 «Убежище», Галерея Зенит, Вашингтон, округ Колумбия
1985 «Работы на бумаге», Центр искусств школы 33, Балтимор, Мэриленд
1984 «Взгляд», Галерея Университета Мэриленда, Катонсвилл, Мэриленд,
1983 «Конструкции», Центр искусств школы 33, Балтимор, Мэриленд,
1983 «Artscape», Балтимор, Мэриленд
1982 «Artscape», Балтимор, Мэриленд
1980 «Скульптура 80», Институт искусств Мэриленда, Балтимор, Мэриленд,
1979 «Групповая выставка», Галерея предложений, Балтимор, Мэриленд
1979 «Балтимор Фестиваль искусств», Балтимор, MD
1978 «Новые художники», Галерея Флит-Стрит, Балтимор, MD
1972 «Групповая выставка OHO», Галерея Студенческого центра, Белград, Югославия
1971 «Групповая OHO-Биеннале в Париже», Париж, Франция
1970 «Group OHO», Munich Kunstverein, Мюнхен, Германия
1970 г. «Информация», Музей современного искусства, Нью-Йорк, штат Нью-Йорк
1970 г. «Primavera Festival», Флоренция, Италия
1969 г. «Предки-OHO», Moderna Galerija, Любляна, Республика Словения
1969 г. «OHO Group», Center Galerija , Загреб, Югославия
1968 «Group OHO», Galerija 212, Белград, Югославия
1968 «Фестиваль искусств Фьюмальбо», Фьюмальбо, Италия

Гранты и награды

2004 Региональный совет по искусству и культуре, Portable Works Collection, Portland1 OR 9000 1 999 Один процент за покупку произведений искусства, Юридический центр Орегона Найт, Юджин, ИЛИ
Премия «Один процент за покупку произведений искусства», 1997 г., Библиотека Университета штата Орегон, Корваллис, штат Орегон
Грант для индивидуальных художников, 1991 г., Комитет мэров по искусству и культуре, Балтимор, штат Орегон,
Грант, 1981 г. Грант Works in Progress, Совет искусств Мэриленда, Балтимор, Мэриленд

Перформансы

1983 «Ядерный бейсбол», Washington Project for the Arts, Вашингтон, округ Колумбия
1982 «Beyond the Jet Set», Фестиваль исчезающих искусств, Балтимор, Мэриленд
1980 «Эскимосский пирог», Центр искусств школы 33, Балтимор, Мэриленд
1981 «Слепое пятно», Центр искусств школы 33, Балтимор, Мэриленд
1982 «Застывшие моменты», Мэрилендский университет округа Балтимор, Катонсвилл, Мэриленд,
Театр Мандала», Университет Джона Хопкинса, Балтимор, Мэриленд,

Reviews

2008      «Лучшее на Artforum» Кристин Мейсел, Artforum, стр. 269, декабрь.
1991 «Art a la Carte», Кэрол Вуд, Baltimore City Paper, 23 июля.
1992 «Artscape», Джон Дорси, Baltimore Sun, 19 июля..
1986 «Скульптура городского эффекта», Джоанн Льюис, Washington Post, 5 июля.
1985 «Искусство в печати», Baltimore City Paper, 6 декабря. 18 сентября.
1982 «Артисты андеграунда», Боб Грин, журнал Baltimore Sun, 7 марта.
1970 «Третья программа», Белградское телевидение, Белград, Югославия 21, Биляна Томич, Белград, Югославия
1970 Арт. 20, Брацо Ротар, Белград, Югославия
 
Каталоги/Книги

2005 г. «Живое искусство на краю Европы», каталог, Музей Кроллера-Мюллера, Оттерлоо, Нидерланды
1994       «OHO Retrospektiva», каталог, Moderna Galerija, Любляна, Словения

Las aporías de Zenon de Elea

0 Сигнальные ракеты 0 Сигнальные ракеты ×

Aporía: del griego aporía («пасо невыполнимо», «camino sin salida»). Con эль término aporía Nos Referimos а-ля Situacion Que Se Crea Cuando ип Problema Carece де Solución о да Лугар a умозаключения absurdas.

Зенон де Элеа (s.V.a.C.), disípulo de Parménides, защитивший тезис де су маэстро, представляющий уна серию де аргументос, дие большинстворабан эль-характер абсурдо де лас тезис дель movimiento y de la multiplicidad del ser. Аристотель считает изобретателем диалектики. Sumé todo consió en lo que ahora llamamos la demostración косвенная или редукция аль абсурдо: demostración косвенная де уна tesis mediante la reducción al absurdo de la tesis contraria.

El procedimiento empleado en sus aporías (« aporía » es un problema sin salida o sin solucion) es la reducción al absurdo , que состоящий en demostrar una tesis mediante es fsualsaor de prueba de . En este caso, la tesis que se претенденте demostrar эс ла де ла imposibilidad дель movimiento.

 

•   1ª Апория, дикотомия. Un móvil, para recorrer una distancia, ha de pasar antes por la mitad de esta distancia, y antes todavía por la mitad de esta mitad и т. д., y así infinitos puntos. Pero un número infinito de puntos no puede recorrerse en un tiempo finito… igual que un baston al que se le cercenase la mitad cada día, sería inacabable.
• 2ª Апория, де-Акилес-и-ла-Тортуга. Aquiles da una ventaja a la Tortuga, y se da la salida. En el tiempo Que Aquiles tarda en llegar al punto de partida de la Tortuga, ésta se ha movido algo, por lenta que se mueva. Y nuevamente Aquiles empleará algún tiempo, por rapido que corra, en llegar al punto que ha alcanzado la tortuga.-Y Aquiles no adelanta nunca a la tortuga.
• 3ª Aporía, de la flecha. Si se supone que el tiempo está compuesto de Instantes, entonces en cada uno de ellos la flecha ocupa un espacio determinado, y estará inmóvil en el. Así que lo que se mueve no se mueve en el lugar en que está; tampoco, menos aún, donde no está. El movimiento sería una suma de inmovilidades, lo que es absurdo.
• 4ª Апория, дель стадион. Supongamos que en un estadio dos formaciones del mismo número de atletas se mueven en relación a una tribuna que mide lo mismo que las formaciones, a igual velocidad y en sentidos contrarios. Cualquiera de las dos formaciones recorrá la longitud de la tribuna en un tiempo t , y la longitud de la otra formación, que es la misma de la tribuna, en un tiempo t/2 , local significa que la velocidad es непоследовательный. Para nosotros, que hemos asimilado desde Galileo la relatividad del movimiento, esta aporía no es valida; pero para Zenón, que el movimiento sea relativo al punto que рассмотрит возможность фихо, эквивалентно negar que el movimiento tenga determinación alguna.

 

 

 

Парадоха-дель-Эстадио

 

5

Куарта «Para demostrar que la mitad del tiempo puede ser igual al doble del tiempo рассматривать tres filas de cuerpos una de las cuales, ( A) está en reposo, mientras que las otras dos, ( B) y ( C) ), se mueven con igual velocidad en sentidos opuestos:

 

Первая позиция	Вторая позиция

 

En el momento en que todas están en la misma parte del curso (B), habrá sobrepasado double número de cuerpos en (C) que en (A) Por lo tanto el tiempo que ha empleado para pasar ( A) es doble Que el tiempo Que ha empleado para pasar (C) Pero el tiempo Que (B) y (C) han empleado para alcanzar la posición (A) es el mismo. Por tanto el doble del tiempo es igual a la mitad del tiempo” (traducción de Burnet) Es útil imaginar ( A ) como una valla de estacas.

El corredor en el estadio nunca alcanzará su meta: antes de alcanzar el extremo del estadio debe alcanzar su mitad, y antes aún, la mitad de la mitad, y así hasta el infinito, aunque encada tiempo la distancia sea cada vez más pequeña .

Aunque Zenón no presenta la siguiente paradoja, cabría argumentsar del mismo modo en contra de la imposibilidad del tiempo (algo que parece ya rematadamente absurdo): por desgracia, el lector nunca acabará de leer el libro que tiene en sus manos: pongamos que le quedan diez horas de lectura; para que ésta concluya, antes debe transcurrir la mitad de ese tiempo (cinco horas), pero antes la mitad de esta mitad (dos horas y treinta minutos), y antes aún la mitad de la mitad de la mitad (una hora y cuarto) , y así hasta el infinito.

Paradoja de Dicotomía

Caso Especialmente Intuitivo es el de la progresión 1/2, 1/4, 1/8, 1/16, 1/32… Parece Que Que que que que que que. cogemos la mitad de la unidad, y luego la mitad de lo que queda, y luego la mitad de lo que queda, y así «hasta el infinito», acabaremos cogiendo la unidad completa:

 

 

9000 la fórmula anterior para la suma, se tiene:

El caso planteado por Zenón es esencialmente el mismo: supongamos que la distancia a recorrer es L. Entonces los intervalos a recorrer por el atleta serán L/2, L/4, L/8…, cantidades que resultan ser los términos de una progresión geométrica de razón 1/2 cuya suma es:

 

Es decir, que no hay Problema en subdividir el espacio infinitamente.

¿Y el tiempo?

Si la velocidad del atleta es v (рассматривается постоянная связь с товаром), el tiempo que tardará en recorrer el primer intervalo será L/2v, y el segundo L/4v, y así sucesivamente. Zenón en este punto dice Que el corredor nunca podrá llegar а-ля мета porque recorrer лос infinitos intervalos ле llevaria ип tiempo infinito. Pero se quivoca: si sumamos todos los tiempos, tenemos:

 

que es una cantidad de Un tiempo finita.

 

 

Argumento de Aquiles y la tortuga

 

A :  Aquiles T : Tortuga

t ₀ , t ₁ , t ₂ , t ₃ , : tiempo 0 o salida, tiempo 1, tiempo 2, … , tiempo 30005

El más rápido de los hombres, Aquiles, no podrá alcanzar nunca al más lento de los animales, la tortuga, si en una carrera se da a esta una ventaja inicial: supongamos que Aquiles le da a la tortuga una ventaja de 100 metros . Para facilitar la comprensión pongamos Que Aquiles sólo corre diez veces más rápido que la Tortuga; en el t0 Aquiles está en la salida y la Tortuga в 100 метрах; en el t1 (pongamos que 15 segundos) Aquiles recorre 100metros y la tortuga 10; en el t2 (que es 1/10 de t1 = 1,5 segundos) Aquiles llega al punto en el que antes estaba la tortuga y ésta recorre 1 metro; en elt3 (que es 1/10 de t2 = 0,15 segundos) Aquiles recorre este metro pero la tortuga recorre un decímetro; y así sucesivamente.

Эстратегия аргумента состоит в том, чтобы учитывать время, прошедшее с большим количеством запросов, точное определение пропорции в отношении Aquiles le aventaja a la Tortuga en velocidad (1/10), de este modo, aunque en tiempos y en distancias cada vez más pequeñas (уна décima parte en Cada tiempo рассматривать) Aquiles nunca alcanzará а-ля Tortuga, у así ла tortuga irá llevando ла ventaja hasta espacios infinitamente pequeños. Recorrer ип número infinito де puntos parece suponer, порт tanto, recorrer ип tiempo infinito.

Aquiles no podrá alcanzar jamás a la Tortuga aún cuando, очевидный, se vaya aproximando infinitamente a ella.

Con estos arguments, Zenón fighte la doctrina de la escuela pitagórica que afirmaba que los números gobiernan el mundo, que todo guarda una relación basada en números.

 

Se puede probar matemáticamente de «falsedad» del argumentso de Aquiles. Veamos un razonamiento tomado de la página del profesor Bert Wachsmuth de la Universidad de Seton Hall en USA.