I. Платон и геометрия (1957). Открытое общество и его враги
I. Платон и геометрия (1957). Открытое общество и его врагиВикиЧтение
Открытое общество и его враги
Поппер Карл Раймунд
Содержание
I. Платон и геометрия (1957)
Во втором издании этой книги я существенно дополнил примечание 9 к главе 6 (с. 308-315). Выдвинутая в этом примечании историческая гипотеза впоследствии получила развитие в моей статье «Характер философских проблем и их научные корни» (К. Popper. The Nature of Philosophical Problems and Their Roots in Science // British Journal for the Philosophy of Science, 1952, vol. 3, pp. 124 и след.; впоследствии она была включена в мою книгу «Conjectures and Refutations»). Ее можно сформулировать в таком виде:
(1) Открытие иррациональности квадратного корня из двух, которое привело
к краху пифагорейской программы сведения геометрии и космологии (и,
по-видимому, всего знания) к арифметике, вызвало кризис греческой
математики.
(2) «Начала» Евклида представляют собой не учебник геометрии, а скорее последнюю попытку платоновской школы преодолеть этот кризис путем перестройки всей математики и космологии на фундаменте геометрии (что означало инверсию пифагорейской программы арифметизации) для того, чтобы иметь дело с проблемой несоизмеримости на систематической основе, а не ad hoc.
(3) Именно Платоном была впервые задумана программа, впоследствии
реализованная Евклидом: Платон первым осознал необходимость перестройки
и, выбрав геометрию в качестве нового фундамента и метод геометрических
пропорций в качестве нового метода, выдвинул программу геометризации
математики, включая арифметику, астрономию и космологию; именно его идеи
легли в основу геометрической картины мира, а, следовательно, и
современной науки — науки Коперника, Галилея, Кеплера и Ньютона.
Я высказал предположение, что знаменитая надпись над входом в платоновскую Академию (см. с. 308, (2)) имела в виду эту программу геометризации. (То, что было намерение провозгласить инверсию пифагорейской программы, подтверждает Архит — см. Diels-Kranz, фрагмент А.)
На с. 310 я высказал предположение о том, что «Платон был одним из
первых создателей специфически геометрической методологии, цель которой
состояла в спасении того, что можно было в математике спасти, и в
покрытии издержек «краха пифагореизма», охарактеризовав это
предположение как «весьма смелую историческую гипотезу». Я не считаю
отныне эту гипотезу столь уж сомнительной. Напротив, теперь я чувствую,
что, прочитав заново в свете этой гипотезы сочинения Платона,
Аристотеля, Евклида и Прокла, можно получить столько подкрепляющих ее
свидетельств, сколько трудно было бы даже вообразить.
Я думаю,
чтоможно перевести просто как «алогичный» (см. также «Горгий», 496 а/b и
522 е). Эта деталь важна для интерпретации названия утерянного сочинения
Демокрита, упомянутого на с. 309.Моя статья «The Nature of Philosophical Problems and Their Roots in Science» содержит ряд идущих еще дальше предположений, касающихся платоновской геометризации арифметики и космологии в целом, осуществленной им инверсии пифагорейской программы, а также его теории форм.
Добавлено в 1961 г.
Поскольку это «Дополнение» было впервые опубликовано в 1957 г., в
третьем издании настоящей книги я почти случайно обнаружил интересное
подтверждение сформулированной мною исторической гипотезы (см. пункт (2)
первого абзаца этого «Дополнения»). Речь идет об одном месте в
комментариях Прокла к Первой книге «Начал» Евклида (ed. Friedlein, 1873,
Prologus II, p.
71, 2-5), ясно показывающем, что существовала традиция,
рассматривавшая евклидовы «Начала» как платоновскую космологию,
т. е. как разработку проблематики «Тимея».
1. Геометрия как физика. Геометрия как математика
1. Геометрия как физика. Геометрия как математика Математика родилась как ответ на выдвинутую развитием общественной практики потребность в познании количественных соотношений и пространственных форм объективной реальности. Первоначально не возникало сомнений§ 39. Геометрия
§ 39. Геометрия Так же на связи положения частей пространства основана вся геометрия. Поэтому она должна была бы быть разумением этой связи; но так как оно, как сказано выше, посредством понятий невозможно, а дается только созерцанием, то каждый геометрический закон
2.
Геометрия неевклидова2. Геометрия неевклидова Лобачевский, обнаружив неевклидову геометрию, разрушил математический аргумент Кантовской трансцендентальной эстетики. Вейерштрасс доказал, что непрерывность не предполагает бесконечно малые величины; Георг Кантор создал теорию
3. Геометрия, эвклидова и неевклидова
3. Геометрия, эвклидова и неевклидова Геометрия проливает не больше света на природу пространства, чем арифметика – на количество населения в США. Геометрия – это целое собрание дедуктивных наук, основанное на соответствующем собрании наборов аксиом. Один набор аксиом
2. Платон
2. Платон а) Разнообразные, спутанные и часто противоречивые материалы из Платона по вопросу о мимесисе мы уже подвергли подробному изучению (ИАЭ III 32 – 56). Повторять здесь этот анализ мы не будем, и приводить кричащим образом противоречивые тексты из Платона мы здесь тоже
11.
То же. Платон11. То же. Платон В сравнении с рассмотренными сейчас авторами Платон занимает совершенно новую позицию. Он чрезвычайно чутко относится не только к самим пропорциям, установленным раньше него, но и к тому непрерывному становлению, которое между ними совершается и которое
2. Платон
2. Платон В своем употреблении термина»стойхейон»Платон, вообще говоря, движется в плоскости еще досократовских установок, но придает им небывалое диалектическое заострение.Стойхейон у Платона есть то, что имеет значение только в связи с какой нибудь цельностью, в
ГЛАВА IV: Непротиворечивость, полнота и геометрия
ГЛАВА IV: Непротиворечивость, полнота и геометрия Смысл явный и неявныйВ главе II мы видели пример того, как смысл — по крайней мере, в относительно простом контексте формальных систем — рождается из изоморфизма между управляемыми правилами символами и вещами реального
ПЛАТОН
Посмотрела на часы. Только начало шестого, а сна ни в одном глазу. Девочка села в кровати.Почему она лежит одетая? И тут вспомнилось вчерашнее. Подставив скамеечку дляАрхитектура, геометрия и нумерология
Архитектура, геометрия и нумерология 345. Blackwell, William. Geometry in Architecture. Emeryville (Са), 1984.346. Bloomer, Kent. Nature of Ornament: Rhythm and Metamorphosis in Architecture. New York, 2000.347. Evans, Robin. Te Projective Cast: Architecture and Its Tree Geometries. Cambridge (Mas.), 1995.348. Hautecoeur, Louis. Mystique et architecture: symbolisme du cercle et de la coupule. Paris, 1954.349. Hecht, Konrad. Mass und Zahl in der gotischen
Евклидова геометрия
Евклидова геометрия
Евклидова геометрия — это, попросту говоря, тот самый предмет, который мы изучаем в школе как «геометрию».
Однако я подозреваю, что большинство людей склонны считать евклидову геометрию областью математики, а вовсе не физической Теорией. Разумеется,
26. Священная геометрия: структура тьмы
26. Священная геометрия: структура тьмы В начале было великое космическое яйцо. Внутри яйца был хаос, и в хаосе плавал Пан Ку, божественный Зародыш. Миф о Пан Ку (Китай, третий век) Большинство из нас, думая о пространстве, обычно представляют себе аморфную пустоту, вроде
Геометрия
Геометрия Чтобы понимать пространство, давайте рассмотрим геометрию – структуру пространства. К счастью, большинство людей понимают геометрию легче, чем алгебру. Геометрия образна; она имеет художественную форму и кажется менее абстрактной, чем формулы алгебры.
Священная геометрия
Священная геометрия
В то же самое время, когда в античности были открыты логические формулы и геометрии, существовала и более мифологическая геометрия.
Священная геометрия – это тот аспект математики, который не описан в ее истории, но этот аспект будет важен для нас в
Евклидова и неевклидова геометрия
Евклидова и неевклидова геометрия К 1900 г. большинство математиков и физиков уже утратили контакт со священными силами, стоящими за математикой, или с математикой, которая представляет собой описание Вселенной, отражающей саму себя. По существу, пространства физики были
Мнимая геометрия
Мнимая геометрия Эйнштейн понимал, что для описания Вселенной ему нужно нечто большее, чем евклидова геометрия, но не знал, где это найти. К счастью, у него были хорошие друзья, учившие его математике, в которой он нуждался. Он обнаружил, что математики уже давно думали о
I.
Платон и геометрия (1957)Во втором издании этой книги я существенно дополнил примечание 9 к главе 6 (с. 308-315). Выдвинутая в этом примечании историческая гипотеза впоследствии получила развитие в моей статье «Характер философских проблем и их научные корни» (К. Popper. The Nature of Philosophical Problems and Their Roots in Science // British Journal for the Philosophy of Science, 1952, vol. 3, pp. 124 и след.; впоследствии она была включена в мою книгу «Conjectures and Refutations»). Ее можно сформулировать в таком виде:
(1) Открытие иррациональности квадратного корня из двух, которое привело к краху пифагорейской программы сведения геометрии и космологии (и, по-видимому, всего знания) к арифметике, вызвало кризис греческой математики.
(2)
«Начала» Евклида представляют собой
не учебник геометрии, а скорее последнюю
попытку платоновской школы преодолеть
этот кризис путем перестройки всей
математики и космологии на фундаменте
геометрии (что означало инверсию
пифагорейской программы арифметизации)
для того, чтобы иметь дело с проблемой
несоизмеримости на систематической
основе, а не ad hoc.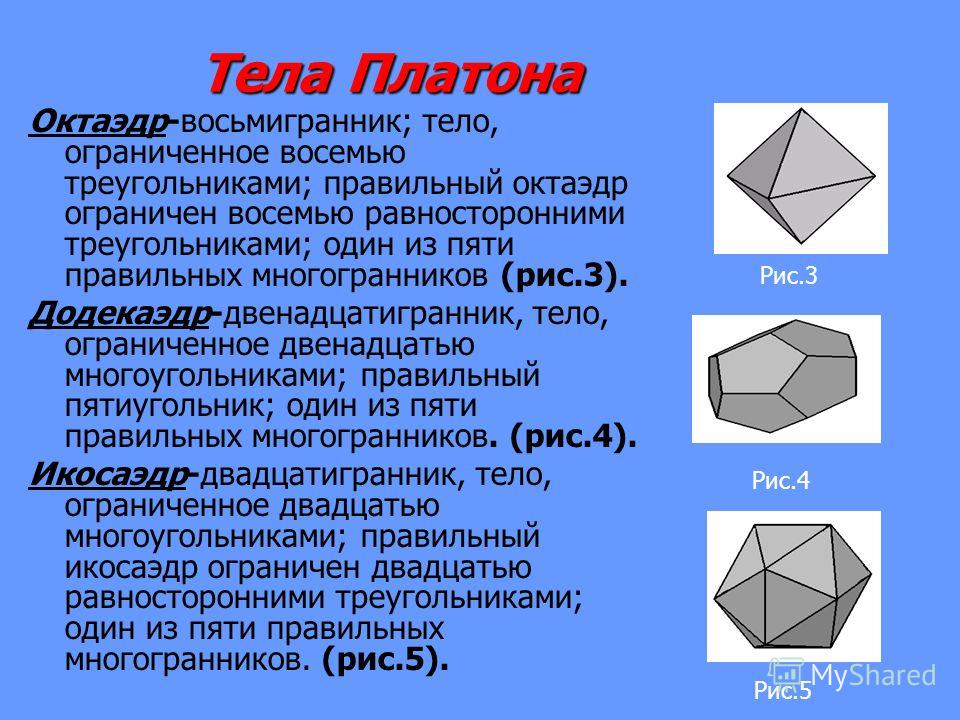
(3) Именно Платоном была впервые задумана программа, впоследствии реализованная Евклидом: Платон первым осознал необходимость перестройки и, выбрав геометрию в качестве нового фундамента и метод геометрических пропорций в качестве нового метода, выдвинул программу геометризации математики, включая арифметику, астрономию и космологию; именно его идеи легли в основу геометрической картины мира, а, следовательно, и современной науки — науки Коперника, Галилея, Кеплера и Ньютона.
Я высказал предположение, что знаменитая надпись над входом в платоновскую Академию (см. с. 308, (2)) имела в виду эту программу геометризации. (То, что было намерение провозгласить инверсию пифагорейской программы, подтверждает Архит — см. Diels-Kranz, фрагмент А.)
На
с. 310 я высказал предположение о том, что
«Платон был одним из первых создателей
специфически геометрической методологии,
цель которой состояла в спасении того,
что можно было в математике спасти, и в
покрытии издержек «краха пифагореизма»,
охарактеризовав это предположение как
«весьма смелую историческую гипотезу».
Я не считаю отныне эту гипотезу столь
уж сомнительной. Напротив, теперь я
чувствую, что, прочитав заново в свете
этой гипотезы сочинения Платона,
Аристотеля, Евклида и Прокла, можно
получить столько подкрепляющих ее
свидетельств, сколько трудно было бы
даже вообразить. В дополнение к
убедительным фактам, на которые есть
ссылка в только что цитированном абзаце,
я хотел бы также обратить внимание на
то, что уже «Горгий» (451 а/b; с; 453 е) относит
обсуждение «четного» и «нечетного» к
компетенции арифметики, тем самым четко
отождествляя последнюю с пифагорейской
теорией чисел, тогда как геометр
характеризуется в нем как человек,
овладевший методом пропорций (465 b/с).
Более того, в другом отрывке из «Горгия»
(508 а) Платон не только говорит о
геометрическом равенстве (см. прим. 48 к
гл. 8), но также вводит неявно принцип,
который позднее был развит им во всей
полноте в «Тимее» и согласно которому
космический порядок есть порядок
геометрический. В этой связи из «Горгия»
следует также, что термин не ассоциируется
у Платона с иррациональными числами,
ибо, как сказано в отрывке 465 а, даже
умение, или искусство, не должно быть
для такой же науки, как геометрия, это
верно a fortiori.
Я думаю, чтоможно перевести
просто как «алогичный» (см. также
«Горгий», 496 а/b и 522 е). Эта деталь важна
для интерпретации названия утерянного
сочинения Демокрита, упомянутого на с.
309.
Моя статья «The Nature of Philosophical Problems and Their Roots in Science» содержит ряд идущих еще дальше предположений, касающихся платоновской геометризации арифметики и космологии в целом, осуществленной им инверсии пифагорейской программы, а также его теории форм.
Добавлено в 1961 г.
Поскольку
это «Дополнение» было впервые опубликовано
в 1957 г., в третьем издании настоящей
книги я почти случайно обнаружил
интересное подтверждение сформулированной
мною исторической гипотезы (см. пункт
(2) первого абзаца этого «Дополнения»).
Речь идет об одном месте в комментариях
Прокла к Первой книге «Начал» Евклида
(ed. Friedlein, 1873, Prologus II, p. 71, 2-5), ясно
показывающем, что существовала традиция,
рассматривавшая евклидовы «Начала»
как платоновскую космологию, т. е. как
разработку проблематики «Тимея».
Платон был прав. Земля состоит в среднем из кубов
Платон, греческий философ, живший в V веке до н. э., считал, что Вселенная состоит из пяти типов материи: земли, воздуха, огня, воды и космоса. Каждая была описана с определенной геометрией, платонической формой. Для Земли такой формой был куб.
Наука неуклонно выходит за рамки догадок Платона, вместо этого рассматривая атом как строительный блок Вселенной. Тем не менее Платон, похоже, что-то понял, как обнаружили исследователи.
В новой статье в Proceedings of the National Academy of Sciences группа из Университета Пенсильвании, Будапештского университета технологии и экономики и Университета Дебрецена использует математику, геологию и физику, чтобы продемонстрировать, что средняя форма скалы на Земле представляют собой куб.
«Платон широко известен как первый человек, разработавший концепцию атома, идею о том, что материя состоит из некоего неделимого компонента в мельчайших масштабах», — говорит Дуглас Джеролмак, геофизик из Пенсильванской школы искусств и наук.
Науки о Земле и окружающей среде и на факультете машиностроения и прикладной механики Школы инженерных и прикладных наук. «Но это понимание было только концептуальным; ничего в нашем современном понимании атомов не происходит из того, что сказал нам Платон.
«Интересно, что то, что мы находим в камне или земле, это нечто большее, чем концептуальная родословная, восходящая к Платону. Оказывается, что концепция Платона о том, что элемент земли состоит из кубов, — это, в буквальном смысле, среднестатистическая модель реальной земли. И это просто сногсшибательно».
Открытие группы началось с геометрических моделей, разработанных математиком Габором Домокосом из Будапештского университета технологии и экономики, чья работа предсказала, что природные породы будут фрагментироваться в кубические формы.
«Эта статья — результат трех лет серьезных размышлений и работы, но она возвращается к одной основной идее, — говорит Домокос. «Если вы возьмете трехмерную многогранную форму, разрежете ее случайным образом на два фрагмента, а затем разрежете эти фрагменты снова и снова, вы получите огромное количество различных многогранных форм.
Но в среднем результирующая форма фрагментов — куб».
г. Домокош втянул в петлю двух венгерских физиков-теоретиков: Ференца Куна, эксперта по фрагментации, и Яноша Торёка, эксперта по статистическим и вычислительным моделям. После обсуждения потенциала открытия, говорит Джеролмак, венгерские исследователи привезли свое открытие в Джеролмак, чтобы вместе работать над геофизическими вопросами; Другими словами, «Как природа позволяет этому случиться?»
«Когда мы отнесли это Дугу, он сказал: «Либо это ошибка, либо это большая ошибка», — вспоминает Домокос. «Мы работали в обратном направлении, чтобы понять физику, которая приводит к этим формам».
По сути, они ответили на вопрос, какие формы образуются, когда камни разбиваются на куски. Примечательно, что они обнаружили, что основная математическая гипотеза объединяет геологические процессы не только на Земле, но и во всей Солнечной системе.
«Фрагментация — это повсеместный процесс измельчения планетарных материалов», — говорит Джеролмак. «Солнечная система усеяна льдом и камнями, которые непрерывно разбиваются на части. Эта работа дает нам сигнатуру этого процесса, которую мы никогда раньше не видели».
Частично это понимание заключается в том, что компоненты, отделяющиеся от ранее твердого объекта, должны подходить друг к другу без каких-либо зазоров, как упавшая тарелка, которая вот-вот разобьется. Как оказалось, единственная из так называемых платоновых форм — многогранников со сторонами равной длины — которые подходят друг к другу без зазоров, — это кубы.
«Одна вещь, которую мы предположили в нашей группе, это то, что, вполне возможно, Платон смотрел на выход скалы и после обработки или анализа изображения подсознательно в своем уме, он предположил, что средняя форма чем-то похожа на куб», — говорит Джеролмак.
«Платон был очень чувствителен к геометрии, — добавляет Домокос. Согласно преданию, фраза «Пусть не войдет никто, не знающий геометрии» была выгравирована на двери в Академию Платона.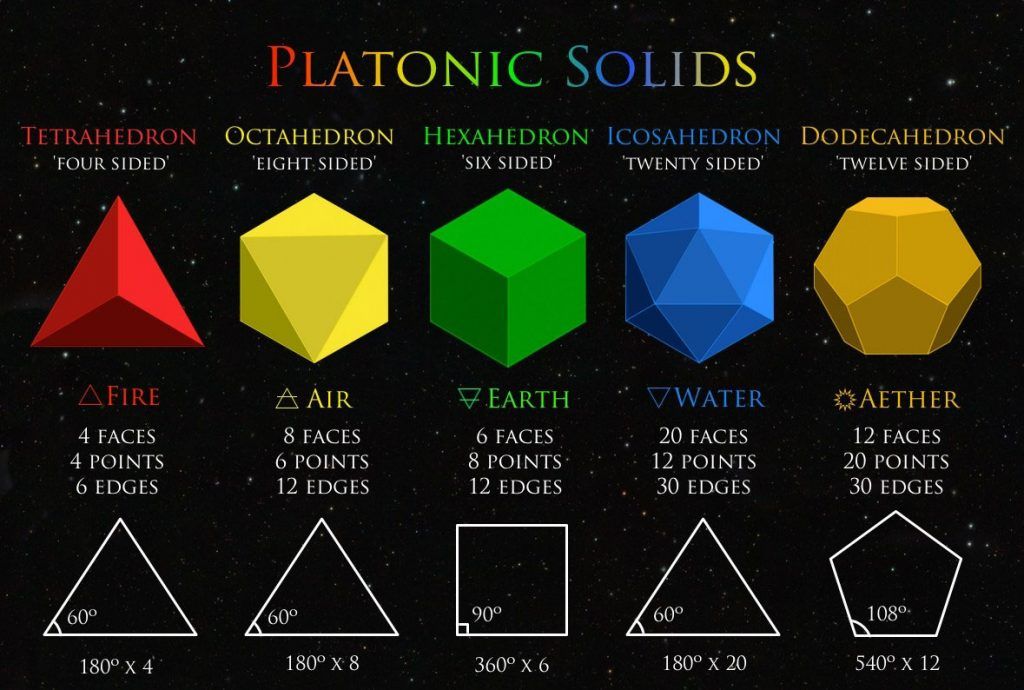
«Его интуиция, подкрепленная его широкими представлениями о науке, возможно, привела его к этой идее о кубах», — говорит Домокос.
Чтобы проверить, соответствуют ли их математические модели природе, команда измерила большое разнообразие горных пород, сотни собранных ими и тысячи других из ранее собранных наборов данных. Независимо от того, были ли камни естественным образом выветрены из-за большого обнажения или были взорваны людьми, команда нашла хорошее соответствие среднему кубическому значению.
Однако существуют особые скальные образования, которые, кажется, нарушают кубическое «правило». Одним из примеров является Дорога гигантов в Северной Ирландии с ее высокими вертикальными колоннами, образованными в результате необычного процесса охлаждения базальта. Эти образования, хотя и редкие, все же охватываются математической концепцией фрагментации команды; они просто объясняются необычными процессами в работе.
«Мир — грязное место, — говорит Джеролмак. «В девяти случаях из 10, если камень разрывается, сжимается или раскалывается — а обычно эти силы действуют вместе — в итоге вы получаете фрагменты, которые в среднем имеют кубическую форму.
Только если у вас особое стрессовое состояние, вы получаете что-то еще. Земля просто не делает этого часто».
Исследователи также исследовали фрагментацию в двух измерениях или на тонких поверхностях, функционирующих как двумерные формы, с глубиной, которая значительно меньше ширины и длины. Там узоры разломов другие, хотя центральная концепция разбиения полигонов и получения предсказуемых средних форм все еще остается в силе.
«Оказывается, в двух измерениях вы с одинаковой вероятностью получите либо прямоугольник, либо шестиугольник в природе», — говорит Джеролмак. «Это не настоящие шестиугольники, но они являются статистическим эквивалентом в геометрическом смысле. Вы можете думать об этом как о растрескивании краски; сила действует, чтобы разорвать краску на равные части с разных сторон, создавая шестиугольную форму, когда она трескается».
В природе примеры таких двумерных структур разломов можно найти в ледяных щитах, высыхающей грязи или даже в земной коре, глубина которых значительно превышает ее поперечную протяженность, что позволяет ей фактически функционировать как двух- габаритный материал. Ранее было известно, что земная кора раскололась таким образом, но наблюдения группы подтверждают идею о том, что картина фрагментации является результатом тектоники плит.
Выявление этих закономерностей в горных породах может помочь в прогнозировании таких явлений , как опасность обвала камней или вероятность и расположение потоков жидкости, такой как нефть или вода, в горных породах.
Для исследователей обнаружение того, что кажется фундаментальным законом природы, вытекающим из тысячелетних открытий, было интенсивным, но удовлетворительным опытом.
«Существует множество песчинок, гальки и астероидов, и все они эволюционируют путем измельчения универсальным образом», — говорит Домокос, который также является одним из изобретателей Гёмбока, первой известной выпуклой формы вместе с минимальное количество — всего две — точек статического баланса.
Выкрашивание в результате столкновений постепенно устраняет точки баланса, но формы не превращаются в гёмбок; последняя выступает как недостижимая конечная точка этого естественного процесса.
Текущий результат показывает, что отправной точкой может быть похожая знаковая геометрическая форма: куб с 26 точками баланса. «Тот факт, что чистая геометрия дает эти скобки для вездесущего естественного процесса, доставляет мне удовольствие», — говорит он.
«Когда вы берете в руки камень в природе, это не идеальный куб, но каждый из них является своего рода статистической тенью куба», — добавляет Джеролмак. «Это напоминает аллегорию Платона о пещере. Он постулировал идеализированную форму, которая была необходима для понимания вселенной, но все, что мы видим, — это искаженные тени этой совершенной формы».
Дуглас Джеролмак — профессор кафедры наук о Земле и окружающей среде Школы искусств и наук и кафедры машиностроения и прикладной механики Школы инженерии и прикладных наук Пенсильванского университета.
Габор Домокос — профессор и директор исследовательской группы MTA-BME по морфодинамике Будапештского университета технологии и экономики.
Ференц Кун — профессор кафедры теоретической физики Дебреценского университета.
Янош Торёк — доцент кафедры теоретической физики Будапештского университета технологии и экономики.
Сакральная геометрия в «Тимее» Платона: цифровое подполье
Следующим после Пифагора в деле распространения основных математических конструкций, не только самих чисел, но опять же и геометрии, как ключевых элементов универсального мирового порядка, является Платон. Говорят, что за пределами Академии, основанной Платоном, была надпись: «Да не войдет никто, не знающий геометрии», и хотя невозможно подтвердить, действительно ли существовала эта надпись, она очень хорошо согласуется с философской системой, которую излагает Платон. в его диалогах, особенно Республика и Тимей , которые охватывают его теорию форм, ее связь с числами и математикой в целом, а также его теорию платоновых тел, которая лежит в основе его физической космологии.
И особенно в платоновской школе, которая, как считается, находилась под влиянием предшествовавших им пифагорейцев, мы видим выдающуюся роль нумерологии и геометрии, которая не зависит от космологических и физических взглядов школы — как возникла Вселенная. и поддерживается, но как можно понять саму вселенную во всей ее великой тайне. Дар математики, геометрии, как священной науки, несомненно, не был изобретен греками, но ее акцент, а также большая часть ее широты и раннего объяснения являются наследием греков.
Влияние математики и нумерологии на философию Платона, вероятно, лучше всего видно позднейшим интерпретаторам его работ, поскольку его Бытие и Становление, а его представление о Добре, представляющем Форму Форм, трансформируется в Единое Нео- Платоническая традиция, принцип которой очень тесно связан с Пифагорейской Монадой. Кроме того, в интерпретациях отрывков из Республики ссылка на числовые и математические конструкции как на вещи, которые могут быть постигнуты только в мыслях, т.
е. примеры Форм или Идеи [1] .
Платоновский « Тимей » дает более систематическое описание роли математики и геометрии в универсальном мировом порядке. Здесь мы можем найти не только некоторые следы пифагорейской мысли (поскольку большое значение придается роли треугольников в формулировке и построении физического мира, один из которых, так сказать, пифагорейский), но и роль геометрии вообще. поскольку он обрисовывает в общих чертах основной набор геометрических форм, которые стали известны как Платоновые тела, которые образуют основную форму и строительные блоки четырех первичных элементов — земли, воздуха, воды, огня — из которых построена физическая вселенная.
В Тимее Платон описывает вселенную, которая живет сама по себе, т. е. Мировую Душу, которая управляется фундаментальным порядком, т. е. пифагорейским космосом . Универсальный порядок, о котором говорит Платон, родственный вечному Бытию, но все же находящийся в движении и управляемый временем , которое, в свою очередь, управляется числом и основными математическими принципами.
Эта концепция времени, его связь с числом и движением самих небесных тел является основной характеристикой Мировой Души, вселенной, и одним из ключевых атрибутов самого космоса.
Платон далее обрисовывает иерархию существ в космосе , которая находится с Демиургом на вершине иерархии, и под ним у вас есть различные боги, которые связаны с небесами, а затем с миром смертных, которые созданы богами, все они созданы через Демиурга и представляют собой проявления nous , или интеллекта Демиурга, принципа, который стал известен как сам Интеллект в более поздних неоплатонических интерпретациях Тимей и заключавший в себе мир Форм и Идей, представляющий собой ядро платоновской метафизики [2] .
В платоновском «вероятном повествовании» ( eikôs logos ) или «вероятной истории» ( eikôs muthos ) вселенского творения, описанного в Тимее , Демиург, или Мировая Душа, формирует телесный мир из двух первоначальных субстанции вселенной – то, что большинство переводчиков именует «Тот же» и «Другой», обозначая свою (Тот же) неделимую природу и делимую природу Другого – и промежуточную субстанцию между двумя и создала два великих круга, внешнее из которых он совершал движение Тождественного, а внутреннее — движение Другого, каждое из которых двигалось в противоположных направлениях.
Затем внутренний круг он разделил на семь частей, чтобы получить 7 небесных сфер или 8, считая самую внешнюю сферу неподвижных звезд, то есть круг Того же самого. [3]
После того, как была установлена сама модель и ее движение, Платон затем помещает самих божественных существ, т. заботиться и создавать конструкцию времени, отражая вечное и неизменное в подвижной модели, созданной самим Демиургом. Боги или планеты, как они сияли в небе, были большей частью сделаны из огня и были самыми божественными из всех созданных существ, а вслед за ними Демиург создал существ земли, воздуха и воды, следуя за ними. четыре основных элемента материальной вселенной, каждый из которых участвует в божественной и разумной гармонии вселенского творения, все они движутся в соответствии с числом и составляют представление человечества о Времени.
Таким образом, время возникло вместе с небом для того, чтобы, порожденные вместе, они могли также вместе и разрушиться, если когда-либо произойдет их растворение; и он был сделан по образцу Вечной Природы, чтобы быть как можно более похожим на нее; ибо в то время как образец существует на протяжении всей вечности, копия, с другой стороны, существует на протяжении всего времени, постоянно существовавшая, существующая и готовая существовать.
А потому, как следствие этого рассуждения и замысла со стороны Бога, с целью порождения Времени, солнце, луна и пять других звезд, носящих название «планеты», возникли для определяющего и сохранение чисел Времени. И когда Бог создал тела каждого из них, Он поместил их на орбиты, по которым двигалось вращение Другого, семь орбит для семи тел.[4]
А потому, как следствие этого рассуждения и замысла со стороны Бога, с целью порождения Времени, солнце, луна и пять других звезд, носящих название «планеты», возникли для определяющего и сохранение чисел Времени. И когда Бог создал тела каждого из них, Он поместил их на орбиты, по которым двигалось вращение Другого, семь орбит для семи тел.[4]Обрисовав в общих чертах сотворение неба и живых существ в том, что Платон называет «операциями Разума», он затем обрисовывает в общих чертах то, что возникло через «Необходимость», начиная снова с четырех элементов (земли, воздуха, огня и вода), которые являются основными составляющими внутри «вместилища» вселенной, кормилицей всего Становления и тем, что содержит копию Мировой Души.
Учитывая, что эти четыре элемента имеют глубину и существуют в трехмерном пространстве, Платон, несомненно, под влиянием атомиста Демокрита и пифагорейцев до него, постулирует, что эти основные элементы в своей основе состоят из геометрических фигур, из которых треугольник является наиболее «справедливый», или наиболее совершенный.
Прямоугольный равнобедренный треугольник и прямоугольный разносторонний треугольник — это те, которые он использует в качестве основных строительных блоков элементов, поскольку из них, говоря геометрически, могут быть построены все остальные треугольники. В свою очередь, из этих треугольных форм он описывает конструкцию того, что стало известно как Платоновые тела, каждому из которых соответствует один из основных элементов. Тела — это тетраэдр или пирамида, связанная с огнем, октаэдр, связанный с воздухом, икосаэдр, связанный с водой, и куб, связанный с землей. [5]
[1] Платон, Республика 7.526a.
См. http://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.01.0168%3Abook%3D7%3Asection%3D526a
[2] См. https://faculty. washington.edu/smcohen/320/timaeus.htm для хорошего краткого изложения космологии Платона, изложенной в Timaeus .
[3] Фактические размеры или, точнее говоря, длины вещества, которое использовалось для создания различных кругов, можно рассматривать как небольшой вариант тетрактиса Пифагора (числа 1, 2, 3 и 4 расположены как размеры треугольника в порядке убывания), поскольку Платон использует тот же ряд цифр, за исключением степени 2 для четных чисел и степени 3 для нечетных чисел, чтобы создать серию, в качестве его основных размеров для различных кругов, которые вылеплены Демиургом для построения небесных сфер являются 1, 2, 4, 8 и 1, 3, 9и 27 соответственно, хотя и не в таком порядке.