ЕВКЛИД | Энциклопедия Кругосвет
ЕВКЛИД (расцвет деятельности ок. 300 до н.э.), также Эвклид, древнегреческий математик, известный прежде всего как автор Начал, самого знаменитого учебника в истории. Сведения об Евклиде крайне скудны. Кроме нескольких анекдотов, нам известно лишь, что учителями Евклида в Афинах были ученики Платона, а в правление Птолемея I (306–283 до н.э.) он преподавал во вновь основанной школе в Александрии.
Сочинения под названием Начала появлялись еще до Евклида. Так, мы знаем о существовании Начал Гиппократа Хиосского (ок. 430–400 до н.э.) и некоторых других авторов, но Начала Евклида превзошли сочинения его предшественников и на протяжении более двух тысячелетий оставались основным трудом по элементарной математике. В 13 частях, или книгах, Начал содержится большая часть знаний по геометрии и арифметике эпохи Евклида. Его личный вклад сводился к такому расположению материала, при котором каждая теорема логически следовала бы из предыдущих.
I книга начинается с определений, недоказываемых постулатов и «общих понятий», а заканчивается теоремой Пифагора и обратной ей теоремой. Со времен античности и до 19 в. неоднократно предпринимались попытки доказать пятый постулат («о параллельных»). Лишь в 19 в. было окончательно признано, что Евклид был прав, полагая, что V постулат невозможно вывести из четырех других постулатов. Отрицание V постулата лежит в основе так называемых неевклидовых геометрий – эллиптической и гиперболической (в первой из них отрицается не только V, но и II постулат). II книга содержит геометрические теоремы, эквивалентные некоторым алгебраическим формулам, в том числе и построение корней квадратных уравнений. III и IV книги посвящены окружности (при работе над ними Евклид мог воспользоваться сочинением Гиппократа). В V и VI книгах излагается теория пропорций Эвдокса и ее приложения, в VII, VIII и IX книгах – теория чисел, в т.ч. формула для «совершенных» чисел, алгоритм Евклида нахождения наибольшего общего делителя и доказательство несуществования наибольшего простого числа.
По мнению многих, X книга – наиболее красивая часть Начал. Она посвящена несоизмеримым величинам (парам величин одинаковой размерности, не представимых в виде отношения целых чисел). Возможно, что в основу этой книги Евклид положил теорию Теэтета (умер в 369 до н.э.). Последние три книги Начал посвящены стереометрии и завершаются доказательством того, что существуют пять и только пять правильных многогранников. Авторство т.н. ХIV и ХV книг сомнительно: ХIV книга, возможно, принадлежит Гипсиклу (ок. 180 до н.э.), а XV книга, быть может, написана Исидором Милетским (ок. 520 н.э.).
Текст Начал сохранился в шести греческих рукописях, датируемых 9–12 вв. Имеются и арабские рукописи того же периода, но они столь же фрагментарны, как и более древние греческие рукописи. Две из ранних греческих рукописей содержат также менее крупные сочинения Евклида – Оптику (геометрические теоремы о прямолинейном распространении света) и Феномены (об астрономии и сферической геометрии).
Последнее сочинение написано в стиле более раннего трактата О движущейся сфере Автолика (ок. 330 до н.э.). Это свидетельствует о том, что Евклид мог позаимствовать форму своих сочинений у более ранних авторов. Сохранились еще два сочинения Евклида, одно на древнегреческом, другое только в арабском переводе. В первом из них (Данные) рассматривается вопрос о том, что необходимо знать, чтобы задать фигуру, во втором (О делении фигур) решается задача о разбиении данной фигуры на другие с требуемыми свойствами формы и площади. (Это сочинение использовал Леонардо Пизанский в трактате 1120 года Практика геометрии.)
Пять дошедших до нас сочинений Евклида составляют лишь малую часть его наследия. Названия многих его утерянных сочинений известны со слов древнегреческих комментаторов: Псевдария (о логических ошибках), Поризмы (об условиях, определяющих кривые), Конические сечения (это сочинение Евклида послужило основой для более обширного сочинения Аполлония с тем же названием), Геометрические места на поверхностях (по-видимому, о конусах, сферах и цилиндрах или о кривых на этих поверхностях), Начала музыки (возможно, с изложением пифагорейской теории гармонии) и Катоптрика (о свойствах зеркал).
Дошедшая до нас Катоптрика, хотя и носит имя Евклида, в действительности представляет собой более позднюю компиляцию, возможно, составленную Теоном Александрийским (ок. 350 н.э.), но не исключено, что в ее основу положено сочинение Евклида, написанное под тем же названием и в той же форме. Арабские авторы приписывают Евклиду и различные трактаты по механике, в том числе сочинения о весах и об определении удельного веса.
Проверь себя!
Ответь на вопросы викторины «Математика»
Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?
Пройти тест
Евклид – древнегреческий математик
Евклид – древнегреческий математик- Рефераты на русском
- Математика
- Евклид – древнегреческий математик
Евклид
Евклид – древнегреческий математик (III века до н.э.) работал в Александрии и написал несколько трудов, которые стали основой для образования и использовались около 2200 лет.
Главный труд Евклида – «Начала» (по-другому «Элементы»). Все книги Евклида основываются на аксиомах – утверждениях, не требующих доказательств. Например, аксиома о точке. Вот ее формулировка: «Точка есть то, что не имеет частей и не имеет величины».
«Начала» Евклида, законченные около 325 года до н. э., оказали значительное влияние на развитие математики вплоть до 19 века. В его 13 книгах систематически изложены существенные разделы математики, являвшиеся итогом ее развития до Евклида. Труд был построен на основе аксиом, постулатов и определений. Пожалуй, самым главным и широко изучаемым постулатом является пятый (одиннадцатая аксиома). Вот его формулировка: «Если дана прямая и точка не лежащая на ней, то можно провести только одну прямую, проходящую через точку и не пересекающуюся с данной прямой».
В книгах VII-IX содержалось учение о числах, представляющее разработки пифагорейских первоисточников. Книги X-XIII посвящены стереометрии и теории иррациональности. Личный вклад Евклида в «Начала», по-видимому, состоял главным образом в систематизации и логическом упорядочении разрозненных результатов его предшественников и современников, а его целью было дать такое связное убедительное изложение элементарной геометрии, чтобы каждое утверждение всего большого сочинения можно было свести к постулатам. Начала Евклида оказали огромное влияние на развитие математики. Евклиду также принадлежат работы по астрономии, оптике и теории музыки.
г. Сумы 14.09.00
Реферат по математике
ученицы 7 «Б» класса ВЮ лицея
Берестовской Дарьи
Евклид
Евклид – древнегреческий математик (III века до н.э.) работал в Александрии и написал несколько трудов, которые стали основой для образования и использовались около 2200 лет.
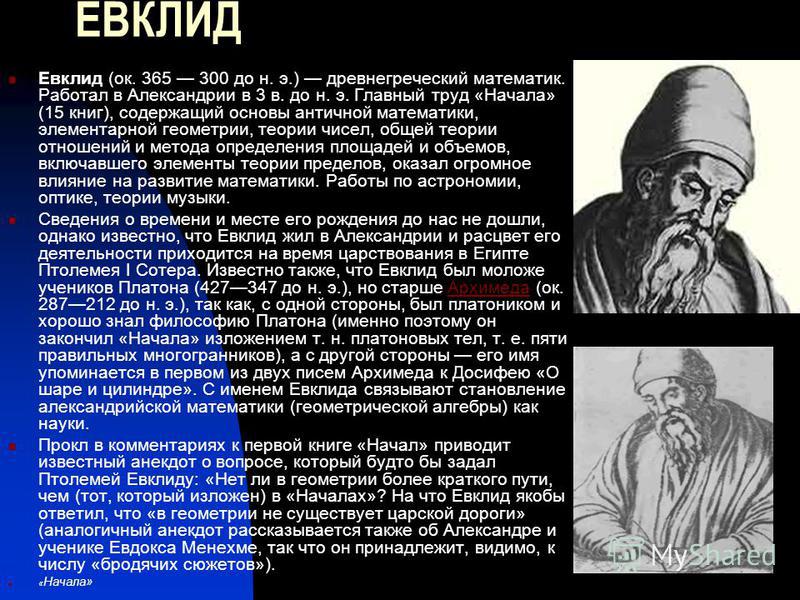
Главный труд Евклида – «Начала» (по-другому «Элементы»). Все книги Евклида основываются на аксиомах – утверждениях, не требующих доказательств. Например, аксиома о точке. Вот ее формулировка: «Точка есть то, что не имеет частей и не имеет величины».
«Начала» Евклида, законченные около 325 года до н. э., оказали значительное влияние на развитие математики вплоть до 19 века. В его 13 книгах систематически изложены существенные разделы математики, являвшиеся итогом ее развития до Евклида. Труд был построен на основе аксиом, постулатов и определений. Пожалуй, самым главным и широко изучаемым постулатом является пятый (одиннадцатая аксиома). Вот его формулировка: «Если дана прямая и точка не лежащая на ней, то можно провести только одну прямую, проходящую через точку и не пересекающуюся с данной прямой».
В книгах VII-IX содержалось учение о числах, представляющее разработки пифагорейских первоисточников. Книги X-XIII посвящены стереометрии и теории иррациональности. Личный вклад Евклида в «Начала», по-видимому, состоял главным образом в систематизации и логическом упорядочении разрозненных результатов его предшественников и современников, а его целью было дать такое связное убедительное изложение элементарной геометрии, чтобы каждое утверждение всего большого сочинения можно было свести к постулатам. Начала Евклида оказали огромное влияние на развитие математики. Евклиду также принадлежат работы по астрономии, оптике и теории музыки.
г. Сумы 14.09.00
Рефераты на русском языке — Математика
Меню
| Главная |
| Новости |
| Краеведение История и современность Герои ВКО Почетные граждане Искусство Театр История театра Деятели театра Музыкальное искусство Народные композиторы Певцы и композиторы Изобразительное искусство Танцевальное искусство Киноискусство |
| Рефераты на русском |
| Рефераты на казахском |
| Литературная карта Усть-Каменогорск Катон-Карагай Курчум Тарбагатай Зайсан Улан Семей Глубокое Риддер Зыряновск Большенарым Аягуз Шемонаиха |
| Образцы документов |
Кем был Евклид? | Издательство Принстонского университета
Макс Эрнст, «Евклид».
1945.
К Бенджамин Уордхо
Евклид Александрийский: математик, автор Элементов геометрии . Автор апокрифических шуток, в том числе знаменитой критики Птолемея I: «К геометрии нет царской дороги». Кто был он? Как он выглядел?
Настоящие биографические подробности скудны: немного больше, чем единичный факт, что его ученики все еще жили в Александрии в середине третьего века, во времена более позднего геометра Аполлония. Таким образом, мы не знаем, был ли он уроженцем Александрии или иммигрантом (как Птолемей) откуда-то еще в греческом мире. Мы точно не знаем, как он выглядел. Но это не остановило людей. Слава его книги означает, что этот человек и его жизнь являются магнитом для переосмысления в зависимости от того, что вы думаете о геометрии и как вы думаете, какое место она занимает в культуре.
На рис. 1 представлена типичная картина эпохи Возрождения. На нем изображен Евклид в классической позе геометра, с делителем или циркулем, наклонившийся, чтобы нарисовать красивую большую диаграмму, чтобы ученики могли ее увидеть. Это была давняя традиция того, как должны были выглядеть геометры: существовала средневековая версия, в которой олицетворенная геометрия сама владела разделителями в интересах иногда крошечных учеников. Существует более поздняя традиция, в которой геометры и математики обычно изображаются примерно в одной и той же позе: от вероятного Архимеда в «Афинской школе» Рафаэля [рис. 1а] до массивной статуи Исаака Ньютона работы Паолоцци, установленной возле Британской библиотеки в Лондоне в 19 году.95 [Рис. 1b]. Известная версия — это видение Уильяма Блейка об Уризене, владеющем «золотым компасом», чтобы навязать математические законы сопротивляющемуся миру [рис. 1c]. Поза подчеркивает физический — иногда неудобный — процесс рисования и отображения геометрических диаграмм, а также тот факт, что геометрию нужно было выполнять перед аудиторией (циркули часто бывают массивными).
Вот средневековый Евклид, с другим набором инструментов и другой позой. Евклид (и это ясно обозначено как он) смотрит на луну и звезды вдоль палки, держа в левой руке сферу или круг на палке, вероятно, предназначенный для какого-то земного шара. Он сидит и одет. Его спутник протягивает ему астролябию; на этикетке написано Герман, и почти наверняка это Герман Хромой, автор трактата об астролябии, а также гимнов Alma Redemptoris Mater и Salve Regina.
На другом конце шкалы направление в древней и ранней современной философии рассматривало геометрию как важное связующее звено между миром явлений и возвышенным: инструмент для направления разума от мира к вечному. Именно по этой причине геометрия изучалась в платоновской школе, и мыслители вплоть до эпохи Возрождения и в 18 и 19 веках продолжали продвигать ее изучение как способ очищения ума и привития правильного рассуждения.
Рисунок 3: Пьетро делла Веккья, «Философы (Птолемей и Евклид со своими учениками)». Середина 17 века. Вот Евклид, который кажется больше философом, чем кто-либо еще, в классической позе «мыслителя» и читает книгу, а не рисует диаграмму. Совершенно иное представление о том, кем был Евклид, и оно является результатом многовекового смешения геометра Евклида с его почти современником Евклидом из Мегары, философом, знавшим Сократа.
В конце концов все идолы падают, и 19-й и 20-й века занялись уничтожением репутации великих писателей и мыслителей. После Лобачевского и Эйнштейна евклидова геометрия больше не была лучшим доступным описанием реального пространства; после новой работы над рукописями в 19 веке исходный текст Евклида все больше и больше казался предметом догадок; и направление мысли 19-го века утверждало, что чрезмерное изучение геометрии не столько улучшает ум, сколько делает вас антисоциальным и даже психически больным. Таким образом, к 20 веку Евклид казался не более чем исполнителем долгоживущего трюка. И в этом контексте Макс Эрнст представил свой знаменитый «портрет» Евклида.
Рисунок 4: Макс Эрнст, «Евклид». 1945 год. Лицо — пустая маска для фигуры, биография которой совершенно неизвестна (есть ли вообще кто-то за ней? Некоторые предположили, что «Евклид» — это название команды).
Одежда принадлежит женщине, что напоминает греческую историю, в которой другой Евклид, переодевшись, пробрался в Афины, чтобы послушать учение Сократа. Геометрические формы фона искажаются на манер неевклидова пространства: они просачиваются и в фигуру переднего плана. Здесь нет ничего стабильного, и любая интерпретация условна.
Элементы Евклида прожили столько же, сколько любой учебник по любому предмету, и его репутация далеко не умерла: хотя справедливо сказать, что современный мир немного проблематизировал его. Если Евклид сейчас кажется неуловимой фигурой, то, возможно, так было всегда, поскольку всегда можно было видеть его и его книгу по-разному: как автора, как философа, как героя практической жизни.
Бенджамин Уордхау — историк математики. Он автор Порох и геометрия: жизнь Чарльза Хаттона, питбоя, математика и научного бунтаря и Как читать историческую математику (Принстон) и редактора Богатство чисел: антология 500 лет написания популярной математики (Принстон).
Он живет в Оксфорде, Англия.
Евклид, отец геометрии
Евклид вошел в историю как один из величайших математиков, и его часто называют отцом геометрии. Стандартная геометрия, которую большинство из нас изучали в школе, называется евклидовой геометрией.
Откройте для себя еще 44 статьи по этой теме
Не пропустите эти статьи по теме:
- История научного метода
- Психология Аристотеля
- Кто изобрел научный метод?
- Медицина
- Греческая астрономия
| Статуя Евклида в Оксфорде (Общественный дом) |
Euclid собрался на общении. , книга под названием «Элементы» (ок. 300 г. до н.э.). Этот трактат не имеет себе равных в истории науки и может смело претендовать на звание самой влиятельной нерелигиозной книги всех времен.
Евклид, вероятно, посещал академию Платона в Афинах, прежде чем переехать в Александрию в Египте.
В то время в городе была огромная библиотека, а наличие папируса сделало его центром книг, что было основной причиной, по которой великие умы, такие как Герон Александрийский и Евклид, обосновались здесь.
Euclid’s Elements
| Euclid’s Elements Title Page (Public Domain) |
Euclid’s great work consisted of thirteen books covering a vast body of mathematical knowledge, spanning arithmetic, geometry and number theory. Книги организованы по предметам, охватывающим все области математики, разработанные греками:
Книги I — IV, и Книга VI: Геометрия плоскости
Книги XI — XIII: Сплошная геометрия
Книги V и X: MAGILUDES and Catios
Книги VII-: IX -IX.
Базовая структура элементов начинается с того, что Евклид устанавливает аксиомы, отправную точку, из которой он разработал 465 утверждений, продвигаясь от своих первых установленных принципов к неизвестному в ряд шагов, процесс, который он назвал «синтетическим подходом».
‘ Он смотрел на математику в целом, но сосредоточился на геометрии, и именно эта дисциплина легла в основу его работы.
Аксиомы Евклида
Евклид основывал свой подход на 10 аксиомах, утверждениях, которые можно принять за истину. Он назвал эти аксиомы своими «постулатами» и разделил их на две группы по пять штук, первая из которых является общей для всей математики, а вторая — специфичной для геометрии. Некоторые из этих постулатов кажутся нам очевидными, но Евклид исходил из принципа, что ни одна аксиома не может быть принята без доказательства.
Первая группа постулатов Евклида — общие понятия:
Вещи, равные одной и той же вещи, равны и друг другу
Если к равным прибавляется равное, получается равенство
Целое больше части
| Из Euclids Elements Book I, Proposition 3 (Creative Commons) |
Остальные пять постулатов относились конкретно к геометрии:
Прямая линия может быть проведена между любыми двумя точками.
Любая конечная прямая может быть неограниченно продолжена в виде прямой.
Для любого отрезка можно нарисовать окружность, используя отрезок в качестве радиуса и одну конечную точку в качестве центра.
Все прямые углы конгруэнтны (одинаковы).
Если прямая линия, пересекающая две другие прямые, дает в результате сумму углов с одной и той же стороны меньше двух прямых углов, то две прямые, если их продолжить на неопределенный срок, пересекаются на той же стороне, что и сторона, на которой сумма углов меньше двух прямых углов.
Евклид чувствовал, что любой, кто может читать и понимать слова, может понять его понятия и постулаты, но, чтобы убедиться, он включил 23 определения общеупотребительных слов, таких как «точка» и «линия», чтобы гарантировать, что могут быть отсутствие смысловых ошибок. На этой основе он построил всю свою теорию плоской геометрии, которая веками формировала математику, науку и философию.