Формальная логика Аристотеля — Libtime

1. Главная
2. Экспертные системы
3. Формальная логика Аристотеля

libre24 Декабрь 2011 7529

В экспертных системах для представления знаний кроме правил могут использоваться символы формальной логики. Напомним, что логика — это наука, изучающая правила формирования обоснованных соображений.

Термин «формальный» означает, что логика, к которой он относится, распространяется только на форму логических утверждений, но не учитывает их значение. Иными словами, в формальной логике рассматривается только синтаксис утверждений и не рассматривается их семантика.

В результате отделения формы от семантики появляется возможность объективно оценивать правильность доказательства, не подвергаясь действию предубеждений, вызванных семантикой. В качестве аналогии, по отношению к формальной логике, может рассматриваться алгебра, в которой правильность таких выражений, как X + X = 2X остается неоспоримым, независимо от того, что обозначает X: количество яблок или аэропланов.

Такое свойство формальной логики является полезной при создании экспертных систем, поскольку позволяет отделить знания от соображений. То есть, высказывания, которые, на первый взгляд, выглядят, как рассуждения, могут, в действительности, выполнять роль знаний.

Формальная логика философа Аристотеля

Важной частью процесса проведения рассуждений является логический вывод выводов из посылок.

На этом основывается наиболее ранняя система формальной логики, которая была разработана древнегреческим философом Аристотелем в IV веке до н.э..

Ключевым понятием Аристотелевой логики является силлогизм. В силлогизме посылки выполняют роль свидетельств, из которых должен обязательно быть сформирован вывод.

Силлогизмы имеют две посылки и один вывод, который из них вытекает. Классический пример силлогизма может иметь следующий вид: Посылка 1: Все люди смертны Посылка 2: Преподаватель — человек Вывод: Преподаватель смертный.

Для графического способа представления силлогизмов хорошо подходят диаграммы Венна. С точки зрения математики, каждый эллипс на диаграмме Венна представляет некоторое множество, то есть коллекцию объектов. Таким образом, механизм теории множеств может быть успешно применен для формального представления знаний в логической модели.

Джордж Буль и символическая логика

Аристотеля силлогизмы оставались фундаментом логики до 1847 года, в котором английский математик Джордж Буль (George Boole) опубликовал первую книгу с описанием символической логики. Одним из новых понятий, предложенных Булем, появилась модификация аристотелевского представление под названием «экзистенциальное значение», согласно которому субъект рассуждений должен существовать.

Например, согласно классическим Аристотелевским взглядам, такое выражение, как «Дед Мороз приносит подарки 31 декабря», не может использоваться, как посылка или следствие, поскольку Деда Мороза в действительности не существует.

Булевы представления, имеющие пока статус современных представлений, позволяют рассуждать о пустых классы объектов. То есть, позволяют создавать логические конструкции для прогнозирования последствий использования результатов последовательности действий, которые планируется получить впервые.

Еще один вклад в развитие символической логики, сделанный Булем, заключался в том, что ученый дал определение понятия формулировкой аксиом.

Формулировка аксиом, согласно Булем, состоит из символов, которые используется для представления объектов и классов, а также операций алгебры — для манипулирования этими символами.

Рейтинг: 5/5 — 2 голосов

Основы формальной логики: как не дать собой манипулировать

Мы начинаем серию материалов о манипулятивных техниках, автором которой выступил известный журналист, редактор (и преподаватель философии) Дмитрий Шишкин. В первой части разберёмся, как связаны казахстанские медийные скандалы последнего времени с древними греками Протагором и Аристотелем.

А связаны они очень даже явно — через приёмы словесного мошенничества, названного 2500 лет назад «софизмом». Древние греки научились распознавать ложь по формальным признаками, пора бы заново овладеть этим знанием и нам. 

Искусство манипуляции людьми появилось вместе с речью. Правильно подобранными словами можно отправлять в атаку на врага или обращать в бегство, ввергать в депрессию или мотивировать к свершениям. Но в целом смысл манипуляции всегда один — заставлять делать или думать что-то, что мы делать и думать не собирались — то есть, использовать нас.

Что не так в противостоянии людей, желающих сохранить урочище Кок-Жайляу диким местом, и теми, кто хочет его застроить? На первый взгляд обычный гражданский конфликт — урбанистов и экологов. Но если обратить внимание на нюансы: когда «экологи» приводят аргументы против застройки, а их в ответ называют «экологическим талибаном», и взглянуть на список логических уловок, составленный древними, становится понятно, что это классический пример применения уловки Argumentum ad hominem («аргумент к человеку/личности» или «атака на человека»).

Или, например, когда вся страна была взбудоражена новостями о распространении менингита, на одном из ресурсов вышла статья «Кто заказал министра здравоохранения Елжана Биртанова?». Это – классическая уловка Ignoratio elenchi («невежественное опровержение» или подмена тезиса). (Подробно об этом во второй части материала).Со

Такие примеры встречаются ежедневно. И мы предлагаем вам учиться разбираться в них не по наитию, а научно.

Немного истории

Софистика

Более 2500 лет назад в Древней Греции активно распространились школы софистики. Там давали уроки начинающим политикам: как при помощи ораторского искусства добиваться своих целей. От философов, также процветавших в древних полисах, софисты отличались в основном тем, что не считали важными какие-то универсальные задачи и теоретические размышления, а главным признавали достижение практической цели.

Интересно, что софистика появилась раньше логики как оформленной науки, и, скорее всего, именно софисты подтолкнули философов к её созданию (в качестве инструмента противодействия демагогам, вводившим народ в заблуждение ради собственных целей).  

«Он (Протагор, живший примерно в период 485 – 410 годов до нашей эры, за сто лет до Аристотеля – прим. авт.) первый заявил, что о всяком предмете можно сказать двояко и противоположным образом… о мысли он не заботился, спорил о словах, и повсеместное нынешнее племя спорщиков берёт своё начало от него», – писал о самом ярком представителе софистов Диоген Лаэртский в своей книге «О жизни, учениях и изречениях знаменитых философов». 

Аристотель побеждает всех

Софистов ругал ещё Платон, а его ученик Аристотель решил положить конец одурачиванию народа (по крайней мере, попытался — мы и сейчас попадаемся на те же самые уловки, что были известны ещё 2500 лет назад). Он создал научную базу формальной логики (которую сам он называл «Аналитикой») и классифицировал логические ошибки, используемые софистами.

В принципе, логическая ошибка и логическая уловка — это одно и то же, просто ошибка допускается несознательно, а уловка специально вводится в речь.  

Аристотель в своём труде «О софистических опровержениях» наглядно показал, что если разложить любой софизм, будет видна специально внедрённая в него ошибка, благодаря которой выводы софиста кажутся логичными. 

После Аристотеля немало в развитие формальной логики внесли римляне Цицерон и Квинтилиан, а затем и средневековые схоласты – мы будем в дальнейшем пользоваться их типологией логических ошибок, так что пусть вас не удивляют латинские термины.

Немного теории

Теория — это самая скучная часть формальной логики, и передо мной стоит трудная задача: уложить в рамки современного «лонгрида» курс, который в институте преподаётся в течение года. Поэтому отсечём всё ненужное современному человеку, имеющему интернет и способному самостоятельно найти недостающие фрагменты. 

Главное, что есть в формальной логике — это её четыре основных закона

Три из них сформулировал ещё Аристотель:

— закон тождества,
— закон противоречия,
— закон исключённого третьего.

А четвертый закон – достаточного основания — был добавлен немецким математиком и философом Лейбницем в начале XVIII века. 

Закон тождества

«…иметь не одно значение — значит не иметь ни одного значения», писал по этому поводу Аристотель в своей «Метафизике». 

То есть каждая мысль и каждый термин в процессе рассуждения должны иметь одно и то же значение. Подмена понятия в ходе рассуждения — это классическая логическая ошибка (или уловка).

Например: 

– Гражданин N хороший человек, скромный и любит ездить на велосипеде.
– Из него получится хороший аким города!

Здесь мы видим, как в первой части утверждения говорится о личных качествах человека, а вывод делается о его профессиональных качествах — что далеко не тождественно.  

Закон противоречия

Два противоречащих друг другу суждения не могут быть одновременно истинными. По крайней мере, одно из них ложно. 

… невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении (Аристотель, «Метафизика»)

Например:

Мы часто встречаем заявления от официальных лиц и даже целых институтов о том, что:

– Народ Казахстана неоднократно демонстрировал свою политическую зрелость, отдавая голоса на выборах президента и депутатов парламента за стабильность!
– Вместе с тем, наш народ не готов пока к выборности акимов и прочим демократическим преобразованиям.

Налицо явное противоречие: получается, народ Казахстана с одной стороны политически подкован, а с другой — настолько дремуч, что не готов к такому элементарному процессу, как выборы акима. 

Закон исключённого третьего

Два противоречащих друг другу суждения не могут быть одновременно оба истинными или оба ложными.

…ничего не может быть посредине между двумя противоречивыми суждениями об одном, каждый отдельный предикат необходимо либо утверждать, либо отрицать (Аристотель, «Метафизика»)

Противоречащими называют такие два суждения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается. 

Например:

– Цензура запрещена!
– Если в интересах общества, то цензура разрешена.

Оба эти утверждения об одном и том же явлении не могут быть одновременно правдивыми или ложными. Если делается исключение, то первое утверждение ложное – «третьего не дано». 

Закон достаточного основания

Всякая правильная мысль должна быть обусловлена другими мыслями, истинность которых доказана.  

…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, – без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны (Готфрид Вильгельм Лейбниц, «Монадология»)

Это, в общем — именно то, чем занимается «Фактчек в Казахстане» — поиском достаточных оснований для публикаций. В отличие от первых трёх законов, которые можно применять формальными методами, просто соотнося какие-то утверждения с правилами, для установки достаточности основания необходимо включать критическое мышление и затем прилагать усилия для проверки суждений, в которых вы засомневались.

Например, самые яркие примеры мы встречаем довольно часто в виде панических слухов, распространяемых через мессенджеры и социальные сети.

В случае со скандалом вокруг заболеваемости менингитом: неверными оказались как утверждения об эпидемии, так и «рецепт», в котором утверждалось, что для профилактики менингита всем необходимо пропить курс антибиотиков (что, как пояснили затем врачи, назначается только людям, контактировавшим с больными).  

На законе достаточного основания также базируется важный юридический принцип: «презумпция невиновности», гласящий, что никто не виновен, пока его вина не была доказана.

В соцсетях и даже СМИ он нарушается настолько часто, практически ежедневно, что примеры вы легко найдёте сами. Людей называют ворами и убийцами до судов, друг друга лжецами безо всяких доказательств и опровержений и т.д.

В следующей части читайте о логических уловках, построенных на нарушении этих законов логики:

• Ignoratio elenchi или «подмена тезиса»
• Argumentum Ad Hominem или «переход на личности»

Дмитрий Шишкин

Журналист, редактор, преподаватель философии. Возглавлял ряд казахстанских общественно-политических изданий.Все материалы Дмитрий Шишкин

Аристотелевская логика: Логика категорий

[Обратите внимание: описание, которое я здесь даю, не отражает исторических мотивов Аристотеля и интерпретации разработанной им логической системы, которая очень сильно связана с его более широким философским мировоззрением.

То, что я здесь описываю, скорее является стандартной интерпретацией аристотелевской логики в том виде, в каком она представлена ​​в современных текстах по символической логике.]

Аристотелевская логика — это логика классов или категорий — поэтому ее часто называют «категориальной логикой».

Вернее, это логика утверждений, которые могут быть представлены в терминах классов вещей, и отношений между этими классами .

Например, высказывание на естественном языке «Все коровы — млекопитающие» будет представлено как отношение между классом коров и классом млекопитающих (а именно, что класс коров является подмножеством класса млекопитающих или, что то же самое, что все представители класса коров также являются членами класса млекопитающих).

Аристотелевская логика дает нам инструменты для представления утверждений следующей формы, которые называются «категориальными высказываниями»:

• Все S есть P
• Некоторые S являются P
• Нет S или P
• Некоторые S не являются P

Они отражают субъектно-предикатную структуру широкого класса высказываний, но, конечно, не всех высказываний.

Категорический силлогизм — это рассуждение, состоящее ровно из трех категорических утверждений (двух посылок и заключения), в которых фигурирует ровно три категорических термина, каждый из которых используется ровно дважды.

Примеры:

1. Все люди — млекопитающие.
2. Некоторые строители — люди.

Следовательно, некоторые млекопитающие являются строителями.

1. Гуси не относятся к кошкам.
2. Некоторые птицы — гуси.
Следовательно, некоторые птицы не относятся к кошачьим.

Аристотель исследовал все логически различные типы силлогизмов, которые могут быть созданы с использованием основных категориальных утверждений, и определил, какие из них являются дедуктивно верными, а какие нет. (В системе Аристотеля есть четырнадцать действительных форм. Средневековые логики дали им всем имена.)

Итак, что представляет собой фрагмент естественного языка, логическую структуру которого способна моделировать аристотелевская логика?

Фрагмент естественного языка, содержащий высказывания с двуместной субъектно-предикатной структурой, где подлежащее и предикатные термы могут быть представлены как классы объектов, а логические отношения между высказываниями определяются отношениями включение, исключение и совпадение между классами.

Вот и все.

Одно из самых увлекательных занятий на уроке символической логики — научиться преобразовывать выражения естественного языка в логический синтаксис конкретной логической системы. Неформально мы называем этот перевод с английского (скажем) на «логический» (по аналогии с «китайским», «японским» и т. д.).

Основное преимущество таких упражнений для студентов-лингвистов состоит в том, что они помогают вам осознать грамматические и логические особенности языка, на которые иначе вы не обратили бы внимания.

Например, легко перевести «Некоторые подростки работают в McDonald’s» , потому что и подлежащее, и сказуемое представляют собой существительных во множественном числе — каждое из которых обозначает класс объектов. Именно для этого была создана категориальная логика.

Существительные во множественном числе могут функционировать как подлежащие или предикатные термины в категориальном утверждении. «Некоторые сотрудники McDonald’s — подростки » так же грамматически правильно сформированы, как и « Некоторые подростки — сотрудники McDonald’s» .

А теперь рассмотрите это утверждение: «Некоторые подростки дезорганизованы» .

Если поменять местами подлежащее и сказуемое, получится следующее: « Некоторые неорганизованные — подростки» . Это уже не грамматически правильно построенное предложение.

Проблема в том, что слово «дезорганизованный» является прилагательным , а не существительным. Прилагательные используются для изменения существительных, они обычно не могут стоять отдельно.

Чтобы записать это в «логике» аристотелевской логики, вам нужно переписать прилагательное как существительное во множественном числе, например:

«Некоторые неорганизованные люди — подростки».

Теперь предметный термин обозначает класс людей, а не просто голое прилагательное.

Еще примеры упражнений по переводу с английского на логический синтаксис аристотелевской логики:

• «Нарушители будут привлечены к ответственности».
  • = «Все нарушители — это люди, которые будут привлечены к ответственности».
• «Требуется сборка».
  • = «Некоторые части этого предмета нуждаются в сборке».
• «Нет боли, нет выгоды».
  • = «Упражнения без физической боли — это упражнения, приносящие физическую пользу».

Весело, правда? Конечно, они могут быть неуклюжими и роботизированными, но эти переводы вносят определенную ясность в то, что на самом деле утверждается.

Аристотелевская логика была разработана таким образом, что позволяет нам переводить многие виды утверждений естественного языка в утверждения об отношениях между классами. Полный модуль по этой теме покажет вам, как переводить утверждения, подобные следующим:

• «Сократ — человек».
  • (Термин относится к физическому лицу)
• «Где дым, там и огонь».
  • (В предметном термине используется наречие)
• «В местном аквариуме есть акулы».
  • (Термин предмета имеет подразумеваемый квантификатор — некоторые акул, не все акулы)
• «Не каждый любовный роман интересен».
  • (нестандартный квантификатор)
• «На арену допускаются только лица с билетами».
  • (Эксклюзивное предложение)
• «Пицца — это здоровое блюдо, если в ней есть овощная начинка».
  • (условные связи)

Аристотелевская логика сильна и оставалась доминирующей системой логики, преподаваемой в университетах в течение 2400 лет. Но как теория дедуктивного рассуждения она имеет важные ограничения. Аристотель рассматривает некоторые формы аргументов как действительные, которых мы сегодня не считаем, и он не включает формы аргументов, которые мы признали бы действительными.

Одна из ироний интеллектуальной истории заключается в том, что, хотя евклидова геометрия является величайшим достижением греческой дедуктивной науки, а теория силлогизма Аристотеля задумывалась как теория дедуктивного доказательства

, , теория силлогизма не может объяснить даже простейшие доказательства в евклидовой геометрии.

Этому есть несколько причин, но главная причина в том, что не все предложения геометрии имеют простую субъектно-предикатную форму. На самом деле их довольно мало. Вместо этого геометрические доказательства имеют дело с отношений между объектами, а система Аристотеля не предназначена для моделирования отношений. Кроме того, не все предложения геометрии имеют только один квантор; они могут по существу включать повторных использований слов «все» и «существует».

Есть и другие причины, но получается так, что даже простые математические выражения и математические доказательства не могут быть представлены в логике Аристотеля, и это связано с выразительными ограничениями системы — она только моделирует 0015 фрагмент естественного языка и рассуждений на естественном языке.

Природа логики Аристотеля

Диалектика — самая мощная и всеобъемлющая теория изменений, доступная в настоящее время. Тем не менее, он остается как в значительной степени неизвестным, так и широко неправильно понятым. Это очень сложная теория, которая почти не поддается определению: действительно, в некоторых кругах ведутся жаркие споры о том, следует ли описывать ее как «теорию», «метод», «форму логики» или просто как «диалектику». Она также коренным образом изменилась за столетия, прошедшие с тех пор, как она была впервые задумана, и существует почти столько же версий диалектики, сколько людей пытаются ее описать.

Здесь я пытаюсь изложить диалектику в том виде, в каком она была сформулирована Аристотелем (382 г. до н. э. – 322 г. до н. э.), а затем развита Г. В. Ф. Гегелем (1770–18310) и применена Карлом Марксом (1818–1883). Диалектика – это универсальная теория, утверждающая, что все связано со всем остальным (хотя некоторые вещи связаны более тесно, чем другие) и что все всегда меняется (поэтому интересно, почему некоторые вещи кажутся статичными), что может быть полезно применено в любой интеллектуальной дисциплине (от квантовой механики до психологии). Но это гораздо больше. 

Диалектика может способствовать более всестороннему анализу отношений между природой и человеческими обществами, между группами и населяющими их индивидуумами, а также между индивидуумом и другими. Это универсальная теория, которая остается в противоречии с преобладающими представлениями о том, как функционирует Вселенная. Далее следует моя попытка представить диалектику таким образом, чтобы он был доступен тому, кто никогда раньше не слышал этого термина, как можно короче, и который содержит в себе все, что полезно для попытки произвести изменения на уровне самости. , группа и все человеческое общество.

Система

Представленная здесь диалектика начинается с аристотелевской логики, но отличается от того, что часто называют диалектикой Аристотеля. Аристотель утверждал, что знание может быть получено путем обсуждения. Первый человек выдвигал бы тезис, второй его противоположность — антитезис, и путем рациональной дискуссии проверялись бы утверждения каждого, устранялась бы ложность и возникал бы более совершенный синтез. Это вполне может иметь место. Но она гораздо более ограничена и гораздо менее полезна, чем диалектика, которую я хочу развить.

Стоит потратить время и усилия, чтобы начать с Аристотеля и его логики, не в последнюю очередь потому, что именно здесь используются и определяются многие термины, которые будут использоваться далее в этом изложении (я выделил самые важные слова полужирный ). Эти же слова существуют в обычном языке, но очень часто с другими или менее конкретными определениями. Это, на мой взгляд, привело к тому, что люди читают авторов, которые полагаются на диалектический анализ, не понимая полного смысла того, о чем говорится. Когда я говорю «люди», я определенно имею в виду и «я». Логика Аристотеля выглядит и ощущается как компьютерный код, почти сводящий все заявления, сделанные в языке, к бинарной форме. Действительно, логика лежит в основе некоторых компьютерных языков.

Мы еще вернемся к термину противоречие при объяснении диалектики, а также организационной науки и теории систем.

Аристотель как естествоиспытатель и как философ стремился классифицировать почти все, от животных до понятий. Действительно, он классифицировал различные аспекты того, что можно узнать о любой вещи. Он перечислил 10 типов информации, которые могут относиться к предмету, и назвал их « категорий ». Категории — это классы информации, которые могут относиться к любой «вещи». Он перечислил их как « субстанция , количество , качество , отношение , место, время, положение, состояние, действие или привязанность». описываются как «случайности», которые могут описывать существенную вещь. Мы можем сказать, что человеческое существо является субстантивным. Это человеческое существо может иметь количество 140 фунтов, качество быть умным, отношение быть вдвое ниже другого человека, место нахождения на рынке и время вчерашнего пребывания. Эти классы информации передаются через предложения, которые имеют подлежащее и предикат, где подлежащее — это вещь, к которой относится информация, а предикат включает информацию.  

В чем преуспел Аристотель, так это в том, чтобы представить целую систему логики, которая упорядочивает информацию обо всех вещах и обо всех вещах. Его очень сложный и обширный аргумент состоит из паутины утверждений, где каждый вывод можно проследить до его предпосылок. Логика изложена посредством пропозиций , определяемых как «утверждение или утверждение, выражающее суждение или мнение». Предложения содержат подлежащее и сказуемое . Субъектно-объектное отношение также является основой для грамматики, формой, через которую язык (по крайней мере, западный язык) организует значение. Мы можем систематизировать все, что знаем о мире, используя всего четыре формы предложения, как показано ниже: весь день светлый, ночи не светлые, некоторые дни теплые, некоторые дни не теплые. Мы можем описать любую вещь, которую мы видим, с точки зрения того, на что она похожа и чем отличается. Субъект — это агент, о котором у нас есть мнение, а сказуемое в грамматике — это предложение, содержащее глагол и утверждающее что-то о субъекте.

Аристотель строит свою логическую систему из предложений, которые подтверждаются истинностью более ранних предложений, на которых они покоятся, и соблюдением законов и правил логики. Эта система логики создает ряд непротиворечивых, внутренне непротиворечивых аргументов . Если мы начнем с двух предпосылок, основанных на наблюдении за материальной реальностью, мы сможем прийти к заключению, которое также будет соответствовать материальной реальности. Каждый вывод из серии аргументов можно использовать в качестве гипотезы, которую затем можно проверить на соответствие действительности, часто с помощью эмпирической науки. Здесь есть значительный риск: если хотя бы одна посылка ложна, огромная и запутанная система логического мышления, в свою очередь, может оказаться полностью ложной. Если вы полностью полагаетесь на логику, вы должны быть уверены в своих предпосылках.

Аристотель начинает свою логическую систему с утверждения: «все s есть р». Это абстрактное утверждение, на данном этапе оно не описывает конкретную реальность. Слово «абстрактный» здесь очень важно. Я собираюсь много использовать абстракцию и абстракцию в представлении диалектики. Здесь я определяю абстрактное как «существующее в мысли или в виде идеи, но не имеющее физического или конкретного существования». Это происходит от латинского abstractus , «увлеченный». Здесь содержание было удалено от символов s и p. «Абстрактный» часто используется как уничижительный термин, например, «это просто абстрактный аргумент». Однако акт абстрагирования невероятно полезен. Математика — это именно такая форма абстракции. Мы знаем, что 1 плюс 1 равно 2. Здесь 1 абстрактно и может представлять что угодно. Но из этого предложения мы знаем, что если у нас есть одна корова и у нас есть другая корова, у нас есть две коровы. Это, очевидно, более полезно, когда используемые термины более сложны. Противоположностью абстрактного является конкретное, часто определяемое как «реальное», «материальное», «существующее». Сегодня довольно сложно не думать о строительном материале. Бетон происходит от латинского concrescere , или «расти вместе».

A, E, I, O

Предложение «все s есть p» настолько абстрактно и так просто, что кажется бесполезным. Но это предпосылка, на которой основывается эта логическая система. Это первичное предложение входит в набор из четырех, представленных Аристотелем, каждое из которых обозначено буквой:

A Все s есть p

E Нет s есть p

I Некоторые s есть p

O Некоторые s не есть p

Здесь «s» и «p» — это условий предложения. Буква «s» представляет подлежащее , которое, в свою очередь, представляет все подлежащие, которые можно использовать в этом предложении. Оно абстрактно в том смысле, что оно отделено от любых реальных примеров. Р в нашем предложении представляет предикат . «s» связано с «p», и предложение устанавливает природу отношения. Мы также можем сказать, что «s» — это , определяемое посредством «p»: в нашем утверждении s стоит само по себе, а p полезно, потому что оно говорит нам что-то о s. Что действительно важно здесь — фактически все, что мы можем узнать из этого утверждения, — это отношение между «s» и «p». Одна из самых важных вещей в диалектике состоит в том, что отношения имеют наибольшее значение, даже больше, чем природа s или p. Диалектика — это альтернатива философии Рене Декарта (159 г.6-1650), который в самых простых выражениях предположил, что разум (человеческое сознание) и материя (все остальное) разделены и что материя механична. Если бы вы использовали декартовский научный метод, вы бы разбили s и узнали, из чего они сделаны. Предполагается, что это поможет нам раскрыть истинную природу «s». В диалектике s определяется его отношением к p. Теперь мы хотим определить это отношение

В нашем основном утверждении «все s есть р» «все» называется квалификатор , а «есть» известен как связка. Аристотеля интересуют отношения между этими утверждениями. Используемые здесь квалификаторы «все» и «нет» описываются как универсальные ; «некоторые», а также «некоторые… не» как в частности . Философия была глубоко озабочена тем, что является универсальным. Если мы знаем, что факт верен для всех вещей, это значительно полезнее, чем знание того, что верно только для некоторых вещей. Меня это интересует, потому что проблемы, с которыми мы сталкиваемся, и решения, которые нам нужны, затрагивают всех нас и приведут всех нас к успеху. Разница между всеми и некоторыми долгое время была фундаментальной для политики: универсальная декларация прав человека логически должна применяться ко всем людям (а не, например, только к мужчинам или белым мужчинам). Различие между всеобщим и частным описывается как различие в количество . Все что-то минус какое-то количество чего-то становится чем-то: и в этом случае что-то есть, а что-то нет.

Описано также отличие определителей «все» и «некоторые. ..есть» от определителей «нет» и «некоторые…нет». Первый (все) именуется утвердительным , а второе (нет) — это отрицательное . Разница между утвердительным и отрицательным описывается как различие качества . Определение и использование отрицательного, а также отношения между качеством и количеством — навязчивая идея диалектики. Отсюда мы можем сделать вывод, что когда происходит изменение количества между всеобщим (всем) и частным (некоторым), происходит также изменение качества между утвердительным и отрицательным. Начнем с того, что «все s есть р», где количество «все» применимо к s. Мы знаем, что s имеет свойство быть утвердительным по отношению к p во всех случаях. Когда мы меняем предложение с «все s есть p» на «некоторое s есть p», мы должны заключить, что «некоторое s не есть p», по крайней мере возможно. Здесь качество s в первом предложении остается утвердительным но из этого следует, что «некоторое s не есть р» возможно, и поэтому s может иметь в некоторых случаях и качество отрицательности. Это означает, что когда мы меняем количество s со всех на некоторые, качество также меняется с утвердительного на возможное как утвердительное, так и отрицательное по отношению к p.

Все это начинает выглядеть полезным здесь и сейчас, когда мы можем вывести одно предложение из одного или двух других в процессе, известном как дедукция . Это один из способов расширения нашего знания за пределы того, что мы можем наблюдать, за пределы наших ощущений. Аристотель использовал следующий пример. Возможно, мы знаем, что «у всех собак четыре ноги». Затем нам говорят, что «Фидо — это собака». Затем мы можем дедуктивно заключить, что у Фидо четыре ноги, без необходимости наблюдать за Фидо. Это очень полезная гипотеза, но ее необходимо проверить на практике. Мы могли узнать новую информацию, например, «Фидо сделали операцию по удалению ноги». Однако статистически вероятно, что у Фидо четыре ноги — полезная информация, если мы покупаем ему в подарок собачьи тапочки.

Предложение, с которого мы начинаем, известно как посылка , а то, которым мы заканчиваем, называется заключением . Действие перехода от начала к заключению состоит в том, чтобы вывести . Если мы начнем с одной посылки, вывод будет непосредственным . Если мы начнем с двух или более посылок, вывод будет опосредованным : первая посылка опосредована второй, чтобы сделать вывод. (Обратите внимание, что здесь «немедленно» означает не «без промежутка времени», а вместо этого «с одной предпосылкой, а не с двумя». использовал). Вот что произошло с Фидо: предпосылка, что Фидо — это собака, опосредована предпосылкой, что у всех собак четыре ноги, чтобы сделать вывод, что у Фидо четыре ноги.

Как мы видим, при представлении аргумента или предложения первое, что нужно сделать, это проверить, согласны ли вы с предпосылками. Если вы не согласны с тем, что у всех собак четыре ноги — некоторые попадали в аварии, — то вам также следует оспорить вывод. Мы можем понять, почему универсальные утверждения более полезны, чем частные утверждения: если вы замените все на некоторые в предпосылке Фидо, вы получите «у некоторых собак четыре ноги» и сможете только сделать вывод, что у Фидо может быть четыре ноги, а может и не быть. Логика более полезна, когда мы можем вывести ряд утверждений из посылки или предпосылок, создавая совокупность знаний из того, что может быть единым фактом. Длинная цепочка предложений, каждое из которых опирается на первое, называется соритом, а сориты с двумя посылками известны как 9.0007 силлогизм .

Атомы

Демократ (ок. 460 г. до н. э. — ок. 370 г. до н. э.), древнегреческий философ и современник Аристотеля, заметил, что каменные статуи выветриваются. Он отметил а. твердые физические объекты будут изнашиваться и терять свои края и б. вещество, которое должно было быть удалено, было невидимо невооруженным глазом. Приняв эти две посылки, он пришел к выводу, что даже большие твердые материальные объекты на самом деле состоят из частей, которые настолько малы, что не могут быть обнаружены человеческим зрением. Он отмечал, что на самом деле все объекты материальной реальности со временем трансформируются. Из этого он сделал вывод, что все материальные объекты были сделаны из объектов, слишком маленьких, чтобы их можно было увидеть. Он описал их как «атомы» или неделимое. Спекулятивная философия, логическая дедукция, привели к знаниям, опередившим естественные науки на тысячи лет.

Аристотель приложил невероятные усилия, чтобы выяснить, что произойдет, если вы измените каждую из различных частей предложения, и что произойдет, если вы наложите одно предложение на другое. Он начал с того, что считал «s» и «p» одинаковыми во всех предложениях, как ученый, изолирующий переменные в эксперименте. Далее он смотрит на то, что произошло бы, если бы вы просто поменяли местами подлежащее и сказуемое; и что произойдет, если вы поменяете определители, заменив «все» на «некоторые» (и наоборот). Сейчас это может показаться мучительно скучным, но позже оно станет увлекательным и полезным — и мы знаем, что должны привести в порядок свои предпосылки, если хотим вывести что-то полезное.

Начнем с непосредственного вывода, потому что это проще. Когда мы начинаем менять местами части посылки, это называется эдукцией (а различные способы называются простой конверсией; конверсией путем ограничения и опровержением). Аристотель установил, что в предложении «все s есть р» нельзя предположить, что можно поменять местами s и р. Все s есть p не эквивалентно всем p есть s (если только s не есть p). Как мы можем просто показать, когда мы меняем местами s и p таким образом, иногда то, что мы создаем, является действительным, а иногда — недействительным. Например, мы знаем, что утверждение «все люди — животные» верно, но мы также знаем, что утверждение «все животные — люди» ложно. Аристотель прошел через постулаты и работал во всех случаях, когда вы могли поменять местами вещи и по-прежнему иметь предложения, которые были логически обоснованы. Вот почему логика полезна — мы можем проверить, является ли вывод, который мы сделали из одной истины, чтобы установить более позднюю, выведенную истину, действительным или недействительным. В какой-то степени это может помочь нам узнать, кому верить, а кому не верить, без необходимости врываться в химическую лабораторию во время поздней ночной беседы в пабе о том, «вся философия бесполезна» или просто «некоторая философия бесполезна».

Аристотель особенно интересовался тем, как все без исключения формы предложения A, E, I и O соотносятся с другими формами, когда s одно и то же в каждом предложении и p тоже одно и то же. Мы знаем, что каждая из четырех форм предложений различна либо по качеству, либо по количеству. Он установил, что в некоторых предложениях вы можете поменять местами подлежащее и сказуемое, и ваш вывод останется верным, но некоторые окажутся ложными. Но мы также можем видеть, что некоторые формы находятся в оппозиции другим — если одно верно, то другое ложно. Совершенно очевидно, что «все s есть р» противоположно утверждению, что «ни одно s не есть р». Оба они не могут быть истинными. Однако «некоторое s есть р» согласуется с «некоторое s не есть р».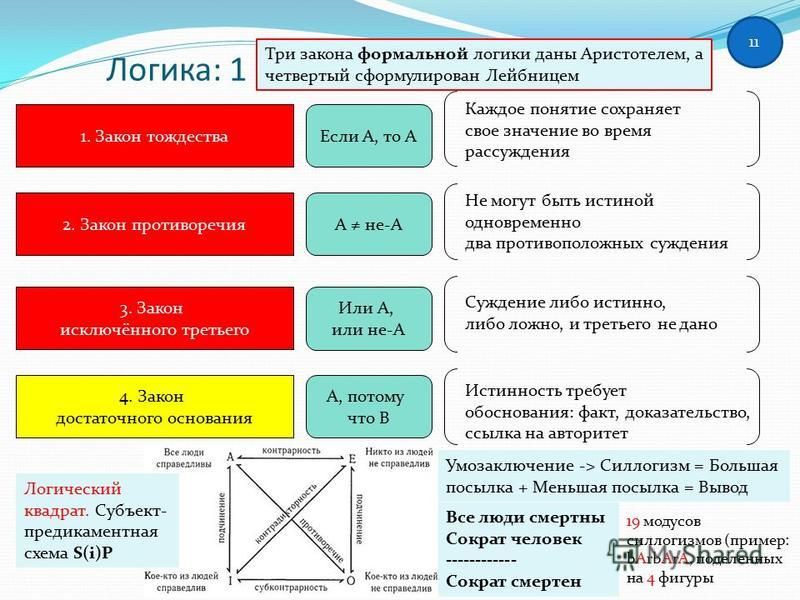 Как мы вскоре увидим, понятие оппозиции, пожалуй, самое важное в диалектике.

Природа оппозиций между предложениями завораживает. Различают четыре вида оппозиции: противоречие , противоречие, субпротиворечие и субатернирование. Это «противоречие» будет для нас наиболее полезным. Предложение находится в противоречии со вторым предложением, когда из истинности первого непосредственно следует ложность второго и, далее, когда из истинности второго непосредственно следует ложность первого. Из этого мы можем видеть, что А противоречит О: если «все s есть р», то мы знаем, что «некоторое s не есть р» не может быть истинным, но ложным. Мы также знаем, что если утверждение «некоторое s не есть р» истинно, то утверждение «все s есть р» ложно. Это определение противоречия в диалектической логике. В обычном языке противоречие часто можно использовать для всех противопоставлений. Однако определение противоположного несколько иное. Здесь мы можем заключить из истинности первой посылки, что вторая посылка ложна; но мы можем только заключить из ложности первой посылки, что вторая посылка истинна или ложна. Итак, если мы знаем, что утверждение «все s есть р» истинно, мы можем сделать вывод, что «ни одно s не есть р» ложно. Но если мы знаем, что утверждение «все s есть р» ложно, мы можем знать только то, что «некоторое s есть р» может быть либо истинным, либо ложным. Таким образом, противоречие является более основательным, а также симметричным.

Со времен Аристотеля в традиционной логике произошли два особенно полезных для нашего анализа развития: акцент на отрицании в девятнадцатом веке, а также современный акцент на высказываниях, в которых термины «s» и «р» являются « категориями ‘, который я объясню более подробно при следующем обсуждении Гегеля. Логика Аристотеля подвергалась серьезной проверке на протяжении столетий с тех пор, как он впервые выдвинул ее. Более поздние разработки, включая концепцию отрицания и концепцию о, расширили и продвинули их.

Отрицательное

Введение отрицательных значений для s и p расширяет и улучшает исходную логику Аристотеля. Профессор Джеймс Викенсон Миллер утверждал в The Structure of Aristotelian Logic в 1938 году, что «отрицательные термины имеют большое преимущество для традиционной логики. С одной стороны, они увеличивают мощность и масштабы системы. С другой стороны, они приводят к подлинному упрощению системы». (стр. 93). Второе из утверждений Аристотеля (E), «no s is p», включает в себя отрицательный квалификатор «no», как отмечалось выше. Однако это расширилось Гегелем и другими, чтобы включить отрицательные значения для самих терминов: «не-s» и «не-р». Теперь у нас может быть предложение «все s не является р» и предложения с двойным отрицанием, такие как «ни одно s не является р». Это можно обозначить как отрицание отрицания, что опять-таки существенно для гегелевской диалектики. Это подводит нас к особо важному моменту. Предложение «все s есть s» теперь не то же самое и не эквивалентно «s есть s», поскольку «все s» включает термин с отрицательным значением «не-s». Предложение «s есть не-s» есть противоречие, оно по определению ложно. «Закон тождества», лежащий в основе диалектики, описывает «s есть s», но не может быть распространен на «все s есть s». Мы вернемся к этому позже.

Вторым недавним дополнением к традиционной логике является введение понятия «класс». Класс или классификация подобны корзине объектов, где эти объекты, собранные в корзину, имеют одну или несколько общих характеристик. Следовательно, «красный» — это класс объектов, которые представляются человеческому глазу красным цветом. Красный класс существует независимо от того, нет ли объектов красного цвета и когда все объекты класса красные. Слова могут функционировать в языке как категории. Слово «люди» относится к тем вещам, которые могут быть классифицированы как «человеческие». У них есть любые свойства, которые идентифицируют их как людей. Предложения, которые мы представили до сих пор, содержат переменные «s» и «p». Эти термины являются пропозициональными функциями. Когда мы заменяем эти переменные термины фиксированным значением, мы получаем предложение. Например, «x — человек» — это пропозициональная функция. Когда переменная x заменяется значением «Энни», мы получаем «Энни — человек», что является верным утверждением. Когда мы заменяем переменную x на Фидо, мы получаем утверждение, что Фидо — это человек, что неверно. Говорят, что те значения, которые заменяют переменную для создания истинного предложения, удовлетворяют пропозициональной функции.

Класс «человек» — это объекты, удовлетворяющие пропозициональной функции «х есть человек». (p85) Наиболее общее определение класса содержится в описаниях «класс, который не имеет членов» и «класс, членство в котором совпадает со всей вселенной дискурса». (p85) Класс без членов называется нулевым классом, а последний называется классом юниверса. Профессор Миллер представил доказательство, демонстрирующее, что включение современного определения и использования класса в традиционную логику непротиворечиво. Далее он утверждал: «Традиционная логика и современная логика находятся в полном согласии друг с другом. Очевидные разногласия между ними отражают просто разницу в словарном запасе … Современная логика, конечно, гораздо более обширная система, чем традиционная логика. [Традиционная логика] действительно является частью Логики, но только частью. Это особый случай».

Преимущество представленной здесь логики — формы чистого разума — состоит в том, что как идеализированная систематизация понятий она не зависит от нашей интерпретации окружающего мира. Наука продвинулась вперед за последние две тысячи лет, но аристотелевская логика осталась такой же надежной и полезной, как и тогда, когда она была впервые развита. Однако использование логики сильно ограничено, когда она не связана с материальной реальностью или не основана на ней.

Реальность

Так чем же нам сегодня полезна логика? Я хочу представить аргумент о природе изменений на личном, групповом и социальном уровне. Этот аргумент относится к нашей материальной реальности: каков мир на самом деле и каковы люди, населяющие этот мир. Первая предпосылка этого аргумента проста: Вселенная состоит из дифференцированной материи. Это утверждение основано на наблюдении, а не на предварительном утверждении. Например, в нашем мире есть вещи, которые мы можем ощущать посредством зрения, звука, осязания, обоняния и вкуса, а есть вещи, которые мы не можем. Для Демокрита, древнегреческого философа, который ввел понятие атома, есть материя и пустота. Это отличается от идеалиста Гегеля, чья система логики не опирается на материальную реальность. Первыми посылками являются понятия чистого бытия и небытия. Отношения между этими понятиями и природой, которую мы ощущаем, очень сложны, и мы вернемся к этому позже.

Вторая предпосылка этой серии состоит в том, что человеческий разум — это дифференцирующая машина. Это также основано на наблюдениях. Благодаря зрению я могу различать световые волны разной длины, создавая ощущение цвета. Мозг — это дифференцирующая машина, но в равной степени это и машина, выявляющая сходства. Он может идентифицировать два яблока как одинаковые, а апельсин как разные. Это дуэльное движение категоризации. Это материалистическое (где мы начинаем с существующей реальности, а не логических понятий), а не идеалистическое основание для большей части того, что следует в нашем определении и обсуждении тождества и различия. Между материальной вселенной и человеческим разумом есть разница. Однако есть и тождество: материальный мир может быть дифференцирован, и человеческий разум может его дифференцировать. Здесь нас интересует тождество — общие свойства, пересекающаяся реальность — между миром и разумом. Это, выражаясь очень простыми словами, и есть то, что Гегель описал как 9.0207 Geist , что переводится как «дух» и «разум».

Цель этой книги — понять изменения в личном, коллективном и общественном масштабе. Каждая из них явно существует на пересечении человеческого разума и материальной вселенной. Следовательно, природа ума (без материальной реальности) и материальная реальность (без ума) — это философская сфера, выходящая за рамки рассмотрения. Спор о том, существует ли диалектика в естественном мире или является просто продуктом человеческого разума, здесь не рассматривается. Но я утверждаю, что мы получим огромную пользу от интерпретации и организации информации с помощью диалектики, поскольку мы пытаемся понять все, что может быть известно человеческому разуму обо всей естественной вселенной.

Этот краткий обзор аристотелевской логики необходим, но недостаточен для моего изложения диалектики. Он вводит определения таких слов, как субъект и сказуемое, тождество, отрицание, отрицание отрицания, непосредственное и опосредованное, противопоставление и противоречие и другие. Эти определения окажутся бесценными, когда мы будем исследовать гегелевское представление диалектики. Мой собственный опыт изучал значение диалектики в обратном порядке: начиная с грубой и неточной версии, которую я узнал от некоторых академических марксистов, затем от моего собственного (неправильного) понимания сочинений Маркса, затем от Гегеля и, наконец, от Аристотеля.