Эратосфен — краткая биография, достижения и открытия — Природа Мира

Содержание

1. Первые годы жизни Эратосфена
2. Жизнедеятельность молодого учёного в Афинах
3. Немного об открытиях и достижениях Эратосфена
4. Переезд в Александрию и смерть

Эратосфен является великим человеком, который внёс огромный вклад в науку. Учёный в первую очередь стал известен в том, что со значительной точностью вычислил окружность Земли. Также философ и одновременно географ работал в таких сферах, как математика, геометрия и даже поэзия. В этой статье мы кратко рассмотрим биографию Эратосфена и узнаем, что он открыл?

Первые годы жизни Эратосфена

Учёный и философ родился в 276 году до нашей эры в Кирене, это небольшой греческий город, который был расположен в северной части Африки. Эратосфен был сыном Аглауса и об его отце ничего неизвестно, поэтому специалисты считают, что родственники учёного не считалась важными в тот период времени.

Даже, не входя в список тех, кто родился в выдающейся семье, Эратосфен смог получить признание в городе, из которого в скором времени переехал.

Молодой учёный всегда стремился к тому, чтобы заниматься подробным изучением многих предметов. Поэтому Эратосфен пошёл по пути популярных учёных и получал знания у главного эксперта по грамматике в родном городе. Стоит отметить, что юноши из богатых семей всегда могли получить образование, но это не мешало бедному ученику поступить в специальную академию для мальчиков.

В Кирене уже с 7 лет обучали литературе, физкультуре и музыке, поэтому творческий потенциал был заложен изначально в Эратосфена и других юношей.

Жизнедеятельность молодого учёного в Афинах

Когда Эратосфен был ещё юным, он интересовался философией, и это являлось его главным хобби и любимым предметом. Само призвание философия, привело учёного в Афины уже в 15 лет, тут он прожил более 20 лет.

Изначально в Афинах молодой юноша нашёл много философов и крайне поразился этому. Сначала юноша поступил к Зенону и учился со стоиками, познакомился с Аристоном, из которого создал биографию. Однако Эратосфен не нашёл так и воодушевляющего стиля, который бы его удовлетворил. Из-за чего был крайне расстроен.

После юный учёный получал знания с платониками, именно в этот период Эратосфен написал произведение, названное «Platonicus». В этом произведение юноша следовал по методу Платона и изучал математические, а также космологически темы.

Недолго юноша изучал философию и даже разочаровался в ней, поэтому решил посвятить жизнь поэзии. И в этот период времени началась слава философа, т.к. в поэзии он добился признания, которого так давно желал.

Писания, конечно, не сохранились от самых первых произведений Эратосфена, но некоторые имена передались потомкам в цитатах других личностей.

Немного об открытиях и достижениях Эратосфена

Эратосфен посвятил много времени чтению, особенно, когда работал руководителем в Александрийской библиотеке. Поэтому он знал, что в летнее солнцестояния в Сиене в полдень солнце стояло над головой учёного. После чего учёный сразу нашёл угол возвышения при помощи гномона. По данным, которые получились у Эратосфена, он смог рассчитать угол солнечных лучей в одной окружности. И вычислил окружность Земли с особой точностью, что стало его главной заслугой.

Учёному было доступно много архивов, в которых найдено расстояние между Сиеной и Александрией, что составляет 5 тысяч стадионов. Также среди изучающих творчество Эратосфена был Колумб, что хоть и не верил в проекции, но понял, когда прибудет в Азию при помощи изучений философа.

Карта мира Эратосфена

Немалый вклад Эратосфен внёс в предмет географию. Ведь учёный нанёс на карту популярные территории, именно в этот период времени Эратосфен ввёл термин «география». Собственные открытия известный философ использовал с точки зрения размеров и форм Земли, чтобы наглядно увидеть.

Также Эратосфен объединил всю информацию, которую получил в области географии и поделил Землю на пять климатических территорий. При помощи вычисления параллелей и меридианов учёный нашёл популярные страны и города. Географ, таким образом, рассчитал расстояние между странами и даже городами. В работах учёного имеется более 300 мест, но проект был потерян.

Ученый являлся не только географом и философом, но и внёс вклад в математические исследования. Эратосфен сделал алгоритм для того, чтобы найти простые числа. Метод состоял из таблиц с натуральными числами. Учёный даже нашёл решение по проблеме Делиана, иначе её называют дублирование куба. Математик сделал прибор, который создан для счёта измерений и пропорций. В математических изучениях Эратосфену помогал Аристотель, вместе они создали мезолабию.

Пускай и люди по сей день не знают, где побывал великий учёный Эратосфен, кроме греческих территорий, но изучения и открытия философа, математика, географа и поэта распространились по всей Земле. Поэтому он считается тем, кто внёс не маленький вклад во множество важных наук.

Переезд в Александрию и смерть

Эратосфен учит в Александрии (работа художника Бернардо Строцци, 1635)

Слава учёного начала бурно привлекать внимание некоторых известных людей, таких как Птолемей 3, именно он ему предложил переехать в Александрию. Учитель плотно занялся репетиторством философа и предложил ему работать директором в местной главной библиотеке.

Учитель Птолемей не только был рад интересу юноши, но и приветствовал его политические взгляды. Когда Эратосфен начал руководить библиотекой, то достиг огромных успехов, которые пошли на пользу учёному. Книги, что самостоятельно читал и изучал Эратосфен, расширили его исследования и принесли славу.

Однако многие упрекали его за то, что он не желает специализироваться на одном предмете и хочет изучать всё. Но ему ничего не мешало воспользоваться положением, а именно руководство библиотекой и Эратосфен продолжал заниматься изучением математики, географии, поэзии и т.д.

Умер учёный в Александрии в 194 году до нашей эры, тогда ему было 82 года. До этого он потерял зрение, и ему пришлось нелегко в последние годы. Поэтому он совершил самоубийство.

Несмотря на то, что всю жизнь учёный любил получать знания в каждой из областей. Вклад в изучение Земли, ему принёс самый важный титул «Отец Географии».

Гугломаг

Спрашивай! Не стесняйся!

Задать вопрос

Не все нашли? Используйте поиск по сайту

Search for:

ЭРАТОСФЕН | Энциклопедия Кругосвет

ЭРАТОСФЕН (ок. 275–194 до н.э.), один из самых разносторонних ученых античности. Особенно прославили Эратосфена труды по астрономии, географии и математике, однако он успешно трудился и в области филологии, поэзии, музыки и философии, за что современники дали ему прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. «второй», по-видимому, также не содержит ничего уничижительного: им желали показать, что во всех науках Эратосфен достигает не высшего, но превосходного результата.

Эратосфен родился в Африке, в Кирене. Учился сначала в Александрии, а затем в Афинах у известных наставников, поэта Каллимаха, грамматика Лисания, а также философов – стоика Аристона и платоника Аркесилая. Вероятно, именно благодаря столь широкому образованию и разнообразию интересов ок. 245 до н.э. Эратосфен получил от Птолемея III Эвергета приглашение вернуться в Александрию, чтобы стать воспитателем наследника престола и возглавить Александрийскую библиотеку. Эратосфен принял это предложение и занимал должность библиотекаря вплоть до своей кончины. Его научные таланты удостоились высокой оценки современника Эратосфена, Архимеда, который посвятил ему свою книгу Эфодик (т.е. Метод).

Сочинения Эратосфена не сохранились, мы имеем от них лишь фрагменты. Трактаты Эратосфена Удвоение куба и О среднем были посвящены решению геометрических и арифметических задач, в Платонике он обращается к математическим и музыкальным основам платоновской философии. Самым знаменитым математическим открытием Эратосфена стало т.н. «решето», с помощью которого находятся простые числа. Эратосфен является основоположником научной географии. В его Географии в 3 книгах содержалась история географических открытий, а также рассматривался ряд физических и математических проблем, связанных с географией, включая указание на сферическую форму Земли и описание ее поверхности.

Однако самым известным достижением Эратосфена в области географии был изобретенный им способ измерения размеров Земли, изложению которого посвящен трактат Об измерении Земли. Метод основывался на одновременном измерении высоты Солнца в Сиене (на юге Египта) и в Александрии, лежащих примерно на одном меридиане, в момент летнего солнцестояния. И хотя остается спорным, получилось ли у Эратосфена в итоге 250 000 стадий (согласно Клеомеду) или 252 000 (по сообщению Страбона и Теона Смирнского), в любом случае этот результат замечателен – диаметр Земли оказался всего лишь на 80 км меньше, чем фактический полярный диаметр. В этой же работе были рассмотрены и астрономические задачи, такие, как оценка размера Солнца и Луны и расстояния до них, солнечные и лунные затмения и продолжительность дня в зависимости от географической широты.

Эратосфена можно считать также основателем научной хронологии. В своих Хронографиях он пытался установить даты, связанные с политической и литературной историей Древней Греции, составил список победителей Олимпийских игр. В трактате О древней комедии, где анализировались произведения афинских драматургов, Эратосфен выступил как литературный критик и филолог. Эратосфен написал также поэму Гермес, повествующую о рождении, подвигах и гибели бога, до нас дошли ее фрагменты. Другой короткий эпос, Гесиод, посвящен смерти поэта и каре, постигшей его убийц. Эратосфен написал также трактат Катастеризмы – описание созвездий и изложение посвященных им мифов (сохранившееся сочинение под таким названием вызывает сомнения в смысле подлинности). Эратосфену принадлежал еще ряд работ по истории и философии, которые не сохранились.

Проверь себя!
Ответь на вопросы викторины «Древний мир»

На какой реке находился древний город Вавилон?

Пройти тест

Размер Земли

Эратосфен и размер Земли

В котором жители причудливых городков Среднего Запада Америки могут взять короткий отпуск и определить размер Земли, используя простые предметы домашнего обихода и немного средней школы арифметика без продвинутой математики, такая как тригонометрия

(Чтобы узнать о родственном методе, нажмите здесь. )

 

Эратосфен измерил это.

Эратосфен не получил уважения. О да, его друзья говорили, что он умный и много знает. Но он никогда не мог сосредоточиться на чем-либо достаточно долго, чтобы стать настоящим экспертом. Его приятели-философы даже называли его «Бета», что означает «второсортный». В конце концов, если вы мастер на все руки, то вы… ну, вы мастер на все руки.

Но для второсортного философа Эратосфен вполне годился. Вероятно, вы впервые услышали о нем в начальной школе. Он разработал знаменитое «решето Эратосфена», которое было первым практическим способом определения того, какие числа являются простыми. Решето до сих пор используется в современной теории чисел. Неплохо для старой Беты.

Но, вероятно, Эратосфен до сих пор удивляет людей тем, что измерил размер Земли. Мало того, мы читали, но он правильно назвал номер. Для этого также не требовалась продвинутая математика, и любой, кто закончил среднюю школу, может легко понять, как он это сделал.

Эратосфен родился в Кирене, Ливия, недалеко от побережья Средиземного моря, и большую часть своей жизни прожил в Египте. Он знал, что в определенный день в Асуане — на юге Египта — полуденное солнце светило прямо в колодец. Или, другими словами, вертикальная конструкция, подобная египетским обелискам, не будет отбрасывать тени.

Но к северу от Асуана, в прибрежном средиземноморском городе Александрия, обелиски

отбрасывали тени в тот день, и Солнце никогда не было прямо над головой 0021 любой день. Эратосфен понял, что причина разной длины теней связана с кривизной Земли. Эратосфен полагал, что по разнице длин теней он теперь вычисляет размер Земли. Конечно, это означает, что Эратосфен знал о том, что Земля круглая, что и так знали греки.

Современные ученые отмечают, что Эратосфен, вероятно, не измерял Землю так точно, как иногда утверждают. Но что его и других греческих математиков интересовало, так это получение числа 9.0021 метод вниз и не беспокоились о том, чтобы получить правильные числа (цитируя Шекспира). И Эратосфен правильно понял метод.

Метод, который Эратосфен использовал для расчета размера Земли, был основан на простом правиле, которое он узнал от Евклида. Правило заключалось в том, что если у вас есть прямая линия, пересекающая две параллельные линии, то

альтернативных углов одинаковы. И он понял, что две параллельные линии — это лучи Солнца.

Альтернативные (и равные) углы

Да, да, это правда, что солнечные лучи, когда они падают на Землю, не точно параллельны. Но поскольку Солнце намного больше Земли, для Эратосфена лучи были достаточно параллельны.

Достаточно параллельных

Теперь, если вы хотите рассчитать действительные числа , вам нужно знать не только метод Эратосфена, но и некоторые эмпирические данные. Во-первых, вы должны знать высоту обелиска в Александрии и длину его тени в полдень 21 июня. Это когда полуденное Солнце находится над головой в Асуане.

Другая необходимая информация — расстояние с севера на юг от Асуана до Александрии. Сегодня мы знаем, что это около 490 миль.

Эратосфен, конечно, пользовался греческими мерками, и мили у них не было. Вместо этого использовалась единица измерения, называемая стадион ( στάδιον ). Это была длина стадиона в Олимпии, где проходили Олимпийские игры. Греческий историк Геродот сказал, что длина стадиона составляет 600 футов, но он использовал греческие футы, которые, по мнению современных ученых, были немного длиннее современного фута. Но мы остановимся на стадионе в 600 футов.

Итак, если Эратосфен говорит, что расстояние от Асуана до Александрии составляет 5000 стадий , это 3 000 000 миллионов футов или 568 миль. Но поскольку Эратосфен, вероятно, говорил о расстоянии вдоль Нила, который немного колеблется взад и вперед, мы пойдем с 500 милями.

ОК. Теперь нам нужно нарисовать схему, показывающую всю систему обелиск-колодец-Земля. Конечно, вы не рисуете его в масштабе, но это не имеет значения. На самом деле, это помогает, если вы этого не делаете.

The Big Picture

Здесь r — радиус Земли (отрезок AB), h — высота обелиска в Александрии (AD), s — длина тени обелиска (AE) , а d — расстояние от Асуана до Александрии (AC).

Во-первых, обратите внимание, что мы изображаем солнечные лучи двумя вертикальными (и, следовательно, параллельными) линиями, CB и DE. Таким образом, линия, проведенная вершиной обелиска к центру Земли, DB, образует два острых чередующихся внутренних угла с солнечными лучами, &угол; ABC и под углом; АДЭ .

Как сказал нам Евклид, эти углы равны.

&угол; ABC = &угол; АДЭ

Итак, все, что вам нужно сделать, это рассчитать размер ∠ ADE , который формируется от основания обелиска ( A ) до вершины ( D ) и затем до конца тени на земле ( E ). Этот угол будет таким же, как угол, образуемый колодцем с центром Земли на обелиск,

&угол; АВС .

Как только размер ∠ ABC в руках, разделите это число на 360. Умножьте это число на расстояние от колодца до обелиска (т. е. от Асуана до Александрии) и, вуаля! Земля.

с

=

360 × D _{Асуан — Александрия} / &угол; АБВ

Так что все сводится к фокусу точно измерение угла ∠ ABC, то, что было трудно сделать в старые времена, и не так просто даже сейчас.

У нас нет оригинальной бумаги Эратосфена (точнее, его папируса), поэтому мы не знаем точных цифр, которые у него были. Но предположим, что он использовал 68-футовый обелиск (например, Иглу Клеопатры) и обнаружил, что Солнце отбрасывает тень длиной 8 футов 7 дюймов.

Что касается измерения высоты обелиска, то это можно сделать разными способами. Один из способов, хотя и не самый практичный, состоит в том, чтобы подождать, пока длина вашей тени не станет такой же длины, как ваш реальный рост. Это означает, что длина тени обелиска такая же, как и его фактическая высота. Или, что еще проще, вы можете в любой момент измерить отношение своего роста к тени и умножить это отношение на длину тени обелиска.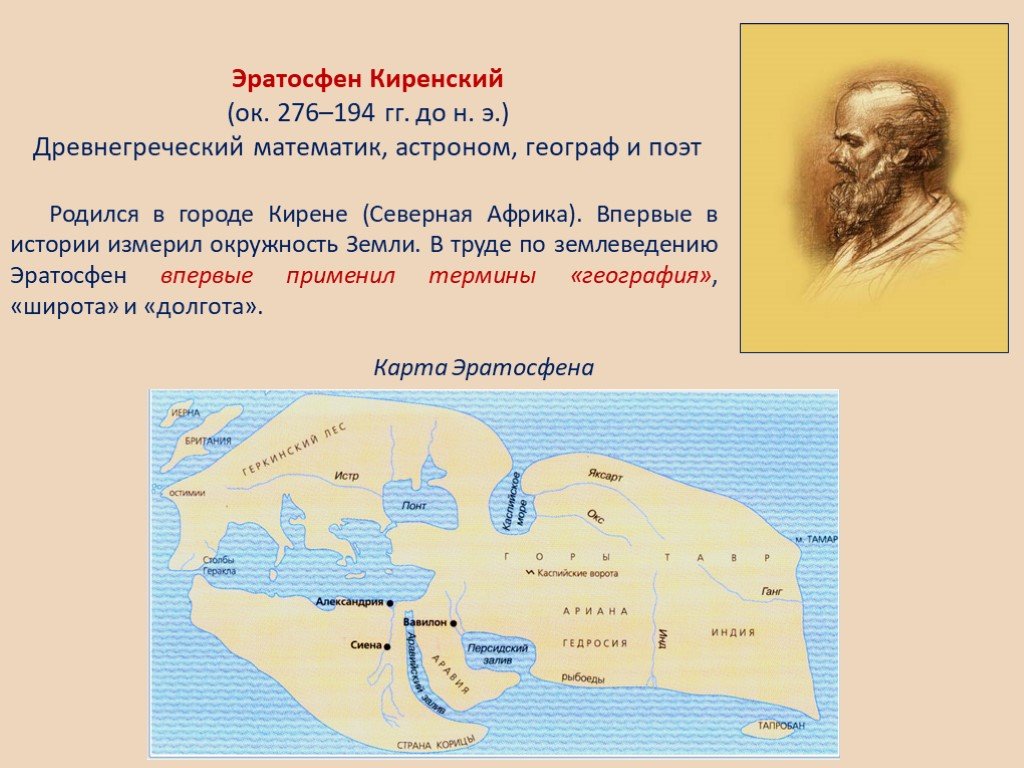

На данный момент нам нужно сделать довольно простую математику. Хотя мы сказали, что можем выполнять арифметику без тригонометрии, сейчас мы продолжим и будем использовать тригонометрию только для того, чтобы получить основы.

Если немного увеличить масштаб обелиска, вы увидите, что обелиск, тень и Земля образуют прямоугольный треугольник (кривая Земли слишком мала, чтобы повлиять на расчет). То есть &угол DAE равен 90 градусам.

Прямоугольный треугольник

Теперь определение

тангенса непрямого угла прямоугольного треугольника представляет собой отношение двух сторон, противоположных и примыкающих к углу .

загар(&угол; ADE)

=

наоборот / Смежные

=

с / ч

Это означает, что если тень составляет 8 футов 7 дюймов (8,58 фута), а обелиск — 68 футов, тангенс угла ∠ АДЭ = 8,58/68 = 0,1262. Если вы посмотрите угол этой касательной — это арктангенс 0,1262 — вы находите угол 7,2 градуса.

тан(&угол; ADE)	=	s / h
	=	8,58 / 68
	=	0,1262

… и …

атан(0,1262) = 7,2 градуса

Но так как ∠ ADE и &угол; ABC — альтернативные углы от параллельных лучей Солнца. Итак, мы знаем, что

&угол; АДЭ = &угол; АВС = 7,2 градуса

Теперь градусы — это не абсолютные числа, а относительные значения того, какую часть окружности охватывает угол. Например, угол в 36 градусов охватывает 100 × 36/360 = 10 % окружности. Угол 90 градусов охватывает 100 × 90/360 = 25 % окружности. Неважно, каков фактический размер круга. 90 градусов охватывают 25% окружности, независимо от того, размером ли он с булавочную головку или — да — размером с Землю.

Таким образом, из вычислений Эратосфена мы знаем, что 7,2 градуса охватывают дугу окружности Земли, которая проходит от Асуана до Александрии. Таким образом, процент окружности между двумя городами равен:

% Окружность	=	100 × 7,2 / 360
	=	2 %

Теперь 2 % такие же, как 1/50 ^-й . Значит, расстояние от Асуана до Александрии равно 1/509.0162-й -й общей окружности Земли. Поскольку расстояние от Асуана до Александрии составляет 500 миль, то окружность Земли в пятьдесят раз больше этого расстояния. Итак:

% Окружность	=	50 × 500 миль
	=	25 000 миль

Согласно последним данным НАСА, окружность Земли составляет 24 900 миль (на самом деле 24 901 миля, но кто считает?). Это всего 0,4 процента от.

Εὕρηκα!

(Что бы это ни стоило, Христофор Колумб обратился к различным источникам, а также рассчитал размер Земли. Он определил, что Земля имеет окружность около 15 000 миль — отклонение почти на 40 %.

Кристофер лучше владел парусным спортом, чем он. по математике.)

Помните, однако, что Эратосфен был заинтересован в правильности метода. Сегодня это означает, что мы вычислим общую формулу для длины окружности. К счастью, это довольно легко сделать. Вы просто выполняете вычисления, используя буквы, и не вычисляете фактические числа.

Помните, что угол между обелиском и его тенью равен углу между двумя городами и центром Земли. Этот угол, разделенный на 360 долей окружности, составляет расстояние от Асуана до Александрии.

А так как угол равен арктангенсу высоты тени и высоты обелиска, то получается:

атан( с / ч ) / 360

=

д / с

Элементарная алгебра затем позволяет нам найти c и эй, вуаля!, у нас есть формула.

с

=

360 × д / атан( с / ч )

Для этой формулы атан ( ^с / _ч ) должно быть в градусах. Но обычно лучше, если вы используете тригонометрические функции, чтобы поместить углы в радиан . Радиан определяется как:

2π Радианы = 360 градусов

… и в радианах формула:

с

=

2π × d / атан( с / ч )

И, как мы увидим, если вы хотите избежать использования тригонометрических функций (а именно это мы и обещали), использование радианов упрощает задачу.

Чтобы избежать тригонометрии, посмотрите еще раз на обелиск в Александрии и колодец в Асуане. Общая схема расчетов:

И снова посмотрите на схему:

Схема

… и формулу с использованием тригонометрии:

с

=

2π × d / атан( с / ч )

Теперь вспомним, что ^s / _h — это тангенс прямого угла, где s и s и h — противоположные и противоположные стороны h 900. 0030 α . Таким образом, арктангенс atan( ^s / _h ) — это просто угол α .

Уравнение примет следующий вид:

с

=

2π × d / α

Теперь в тригонометрии есть широко используемый прием, называемый приближением малых углов . В приближении малого угла, если угол, α , является — кавычки — «достаточно малым» — без кавычек — мы можем написать:

sin(α)	=	α
cos(α)	=	1 —  α 2 / 2
тангенс (α)	=	α

Таким образом, мы можем заменить значение угла α тангенсом, который равен ^s / _h , если угол достаточно мал.

с

=

2π × d / с / ч

. .. можно немного упростить:

с

=

2πhd / с

Насколько мало достаточно мало, вы можете просто вычислить некоторые значения тангенса:

с	h	с / h [tan(α)]	α	Error
0.0	68	0.0000	0.0000	0.00%
5	68	0.0735	0.0734	0.14%
10	68	0.147	0.146	0.75%
15	68	0.221	0.217	1.61%
20	68	0.294	0.286	2.80%
25	68	0.368	0.352	4.34%

So as long as the angle is under around 20 degrees or so we should be all right .

В измерениях Эратосфена много приближений. Расстояние от Асуана и Александрии не по прямой. И эти два города не находятся на прямой линии север-юг.

Также Солнце не сияют прямо в Асуане в любой день. Это потому, что он находится в 45 милях к северу от Тропика Рака. Только в тропиках бывают дни, когда полуденное Солнце находится прямо над головой.

Но расчеты все еще работают по той причине, что ни одна из ошибок не настолько велика, чтобы иметь значение. Даже если Солнце не светит прямо в Асуане, как сказал Эратосфен, это довольно хорошее приближение. Вы всегда можете сделать неверные вычисления, если ошибки достаточно малы, или (что еще лучше) если у вас есть «компенсирующие ошибки». Таким образом, если вы не получите верный ответ, ответ будет достаточно верным.0003

Попробовать дома

Ну, это все и хорошо, если вы живете в Александрии или Асуане, Египет. Но предположим, что вы живете, скажем, в городе Джин Отри, штат Оклахома? Вам навсегда запрещено измерять окружность Земли?

Ну, не бойся! Добрые граждане Джина Отри могут вычислить длину окружности так же хорошо, как Эратосфен. Ключ — как показано ниже — это все, что вам нужно, это два города, разделенные разумным расстоянием с севера на юг, и несколько предметов домашнего обихода.

Точного ответа на вопрос о том, как далеко они должны быть разделены, нет. Но разница длин теней в двух городах должна быть достаточно большой, чтобы ее можно было надежно измерить. Пока вы это делаете, мы можем получить окружность Земли.

Но сначала мы проверим, как это будет работать, взглянув на карту. Там мы видим, что Уичито, штат Канзас, находится почти прямо к северу от Джина Отри, но также и довольно далеко.

От Джина Отри до Уичито

Итак, мы можем создать схему.

Сначала мы проведем самый точный расчет, используя, да, тригонометрию.

Вы помните, что мы показали, что формула из эксперимента Эратосфена с использованием приближения малых углов:

с

=

2πhd / с

. .. где d — расстояние от Асуана до Александрии, h — высота обелиска, а с — длина тени.

Теперь это уравнение работает для любых двух городов, один из которых находится в месте, где в день измерения солнце светит прямо над головой — , а не должны быть Асуаном. Таким образом, мы можем решить уравнение для расстояния d , которое представляет собой расстояние между городами с севера на юг.

г

=

кс / 2πh

Теперь посчитаем расстояние два разных города, которые находятся на заданном расстоянии от города, над которым находится Солнце.

г 1

=

кс 1 / 2πh

и

г 2

=

кс 2 / 2πh

. .. где с ₁ и с ₂ — длина тени. Обратите внимание, что нам нужно только одно значение h , поскольку мы гарантируем, что все, что отбрасывает тени в двух городах, имеет одинаковую высоту.

Теперь возьмем разность двух расстояний, d ₁ и d ₂ :

д 2 — д 1

=

кс 2 / 2πч — кс 1 / 2πч

Можно переставить как:

д 2 — д 1

=

с × (с 2 — с 1 ) / 2πч

И решение для c:

с

=

2πh(д 2 — д 1 ) / (с 2 — с 1 )

Итак, вы видите все, что нам нужно знать длину двух теней ( s ₁ и s ₂ ), высота штифта, h , и расстояние с севера на юг между двумя городами, которое составляет d ₂

5 — 1 d 1 Неважно, где находятся города, если они находятся на линии север-юг.

Конечно, чем больше расстояние между городами, тем лучше, потому что чем длиннее тень, тем точнее ее можно измерить.

Итак, давайте прогуляемся по тропе Санта-Фе — или, как некоторые называют ее, 35-й межштатной автомагистралью США — к Джину Отри, штат Оклахома. На самом деле, вы можете отправиться либо из Оклахома-Сити, либо из Далласа.

Но сначала вам следует найти скобяной магазин и купить 60-дюймовый (то есть 5 футов) стержень для дюбеля. Пока вы в магазине, вы можете купить столярный угольник и сделать отвес, чтобы помочь Вы точно устанавливаете дюбель перпендикулярно

Для тех, кто не знаком с Джином Отри, вы едете по I-35, а затем, когда вы доедете до съезда 40, вы увидите знак, направляющий вас на Оклахомское шоссе 53 на восток в сторону Спрингера, и да, Джин Отри. Если вы выберете выезд и повернете на восток, вы можете проехать около 8 миль, пока не увидите прямо впереди вход в муниципальный аэропорт Ардмора. чуть более полумили вы увидите, что бульвар Джина Отри поворачивает налево и снова возвращается к старой доброй OK 53. Вместо того, чтобы следовать по этому левому повороту, продолжайте двигаться прямо по улице Фрост (OK 53A). Строго говоря, Фрост-стрит будет ти на Мелтон-авеню, хотя кажется, что Фрост просто сгибаясь вправо. Вскоре после этого Мелтон поворачивает налево и превращается в Северную главную улицу. Продолжайте двигаться на юг, и вскоре вы окажетесь на углу Мэйн и Коммерс. Вы в Джине Отри.

Теперь, если вы найдете удобное место для долгожданной передышки, вы можете установить свой стержень. Вы хотите, чтобы он был прочно установлен и перпендикулярен поверхности. Конечно, чем ровнее поверхность, тем лучше, и хочется найти место, где можно провести должное количество времени и не раздражать никого из местных жителей. Если у вас есть 5-дюймовый дюбель, то вы сможете установить его так, чтобы по крайней мере 4,5 фута находились над землей. Но суть в том, чтобы установить дюбель перпендикулярно и точно измерить его высоту над землей.

Строго говоря, вы можете выбрать любой день в году. Но мы выберем 21 июня по причинам, о которых расскажем позже. Однако, какой бы день вы ни выбрали, измерение следует проводить в солнечный полдень . Это когда Солнце находится в самой высокой точке неба.

Конечно, вы можете найти правильное время солнечного полудня (убедитесь, что вы ввели летнее время, если это необходимо). А затем вы измеряете высоту тени.

Но вы также можете определить солнечный полдень, измерив движение солнечного вершина с использованием самой тени. Что вы делаете, так это настраиваете все за пару часов до полудня, делаете повторные измерения длины тени и отмечаете время. Убедитесь, что вы измеряете длину с точностью до шестнадцатой дюйма, а время — с точностью до секунды или около того. Вы продолжаете делать это до полудня. Затем вы можете нарисовать кривую и выбрать время, когда длина тени наименьшая.

Что касается того, какой день лучше, помните, что мы хотим, чтобы отношение тени к высоте штифта было достаточно малым, чтобы наша аппроксимация с малым углом работала. Так что лучший день — летнее солнцестояние или 21 июня. Дни длиннее, и поэтому полуденная тень — самая короткая в году. Итак, треугольники длинные и высокие.

На данный момент, если все d’accord с надлежащей техникой и процедурой, вы обнаружите, что длина полуденной тени 4½-футового стержня в Джине Отри 21 июня составляет около 10 дюймов ³ / ₈ дюймов или 0,8646 фута.

Теперь страница 2 (кто бы это ни сказал).

После того, как вы записали свои измерения — время и длину тени — садитесь в машину. Запишите показания одометра, как только вы повернете на I-35 и направитесь на север в Уичито, штат Канзас. Конечно, это немного — 4 с лишним часа — но вы все равно можете добраться туда, когда светло.

Затем на следующий день — в Уичито много мотелей — запишите, сколько вы проехали, должно быть около 245 миль. Затем установите дюбель, как вы это делали накануне, и заблаговременно до полудня. Снова убедитесь, что вы отметили время солнечного полудня, которое во всех смыслах совпадает со временем Джина Отри.

Измерьте тень и о чудо! Вы должны найти длину тени около 1 фута и 1 ³ / ₄ дюймов или 1,1458 фута.

Следует признать, что два измерения разделены на один день, и лучше всего провести оба измерения в один и тот же день. Вы можете исправить разницу, повторно измерив высоту тени на следующий день в Gene Autry и добавив ½ разницы двух измерений к первому измерению. Но оказывается, что это еще одна ошибка, которая достаточно мала, чтобы не иметь значения, и длина тени практически не изменится. Так что мы просто будем придерживаться 10 ³ / ₈ дюймов.

Итак, теперь мы можем вернуться к нашему уравнению:

с

=

2πh(д 2 — д 1 ) / с 2 — с 1

Теперь разница в расстояниях d ₂  — d ₁ равна расстоянию от Джина Отри до Уичито. Строго говоря, это расстояние с севера на юг, но мы просто остановимся на расстоянии одометра и будем использовать 245 миль.

Теперь мы можем подставить числа:

с

=

2π × 4,5 × 245 / 1,1458 — 0,8646

миль

.. что дает нам длину окружности:

с	=	2π × 4,5 × 245 / 1,1458 — 0,8646
	=	6927 / 0,2812
	=	24634 миль

Учитывая, что «лучшая» современная стоимость составляет 24 901 милю, скидка составляет всего 1 %. Не так уж и плохо, учитывая.

Мы упоминали, что расчет лучше всего проводить в солнечный полдень 21 июня. Однако, если требования современной жизни делают это неудобным, вы можете провести эксперимент в другие дни, хотя вам, возможно, придется использовать тригонометрию.

Например, если вам случится навестить родственников на юге центральной части Оклахомы 21 декабря, вы обнаружите, что тени длиннее, чем летом. Тень Джина Отри от 4,5-футового дюбеля будет примерно 7 футов и 10 ¹⁵ / ₁₆ дюймов или 7,916 футов. В Уичито тень будет 9 футов и 13/16 дюймов или 9,073 фута.

Теперь, если мы используем нетригонометрическую формулу:

с

=

2πh(д 2 — д 1 ) / с 2 — с 1

Подстановка цифр:

с	=	2π × 4,5 × 245 / 9.073 — 7.916
	=	6927 / 1,157
	=	5987 миль

Хм. Не очень хорошо. Так что, эй, случилось?

Ну посмотрите на ракурсы. Тангенс угла в Джине Отри равен ^7,911 / _4,5 . Это равно 1,758. Но арктангенс, то есть угол, равен 1,054 радиана. Таким образом, аппроксимация малого угла ошибочна на 66%! Прибавляя ошибку от измерения в Уичито, получаем ошибку 74%

Однако, если вы пойдете и воспользуетесь тригонометрической формулой.

с

=

2π(д 2 — д 1 ) / атан( с 2 / ч ) — атан( с 1 / ч )

… и цифры:

с	=	2π × 245 / атан( 9,073 / 4,5 ) — атан( 7,916 / 4,5 )
	=	1539 / атан(2.01622) — атан(1.79511)
	=	1539 / 1.11037 — 1.05388
	=	1539 / 0,05649
	=	27084 миль

Что опять же не так уж плохо.

А Эратосфен?

На самом деле, несмотря на современные писания, у Эратосфена дела обстояли не лучше, чем у нас, когда мы ехали из Джина Отри в Уичито.

Заметьте, мы сказали, что в справочниках говорится, что стадион составляет около около 600 футов. Но Эратосфен измерил бы расстояние либо по суше, либо по Нилу. Поскольку Нил в какой-то момент делает петлю север-юг, пройденное расстояние составляет 745 миль. Так что пойдем по суше. Это расстояние составляет около 670 миль. Итак, мили, которые Эратосфен на самом деле насчитал , были:

. Окружность = 50 × 670 миль = 33 500 миль

Значит, он ошибся больше, чем мы ехали от Джина Отри до Уичито. Тем не менее, старый добрый Бета неплохо справлялся, хотя и не был идеальным.

«Измерьте окружность Земли с помощью тени», Бен Финио, Scientific American , 7 сентября 2017 г.

«Эратосфен из Кирены», Архив истории математики MacTutor , Сент-Эндрюсский университет, Шотландия.

Мера за меру , Р. А. Янг и Т. Дж. Гловер, Blue Willow Press, 1996.

«Археологические раскопки Кирены», ЮНЕСКО, http://whc. unesco.org/en/list/190

«Длина тени», PlanetCalc .

 

Эратосфен и тайна стадионов

Автор(ы): 

Ньюлин Уолкуп (Университет Миссури – Канзас-Сити)

Примечание редактора:  статьи студента по математике, спонсируемой организацией History of Mathematics SIGMAA Математической ассоциации Америки.

 

В третьем веке до н. э. блестящий библиотекарь Эратосфен из Кирены (276–195 гг. до н. э.) разработал оригинальный метод измерения окружности Земли. Используя геометрию и Солнце, Эратосфен совершил невозможное. Хотя его оригинальные работы давно утеряны, легендарную историю пересказывают уже более двух тысяч лет. Как и во всех легендах, стало трудно отделить факты от вымысла. Некоторые ученые утверждают, что Эратосфен приблизил размер Земли к 2% от ее фактического значения; в то время как другие считают, что точность его измерения сильно преувеличена. Ключом к этой древней загадке является не совсем стандартная древняя единица длины – стад. Существует большая неопределенность относительно фактической длины стада, который использовал Эратосфен. Также неясно, производил ли он измерения, использованные в расчетах, или полагался на информацию других. Возможно, самый загадочный вопрос заключается в том, почему Эратосфен необъяснимым образом добавил 2000 стадий к своей первоначальной цифре окружности Земли. Эта тайна движет учеными даже сегодня.

Эратосфен был выдающимся ученым древнего мира. Он был хорошим другом известного греческого ученого Архимеда Сиракузского (287–212 гг. до н. э.). На самом деле одно из величайших произведений Архимеда, «Метод», было посвящено Эратосфену [12, с.104].

Я послал вам ранее некоторые из открытых мной теорем, просто написав формулировки и пригласив вас найти доказательства, которые в данный момент я не дал. […]  Доказательства этих теорем я послал вам. Кроме того, видя в тебе, как я уже сказал, серьезного ученика, человека, выдающегося в философии, и поклонника […] [13, с. 12-13]

 

Поскольку Эратосфен был хорошо осведомлен во всех областях науки, но не был «Альфой» (величайшим) ни в одной области, его сверстники дали ему прозвище «Бета» [12, с.104]. Эратосфен получил эквивалент высшего образования в Афинах, а затем отправился в египетский город Александрию [1, с.388]. Привлекая ученых и студентов со всего древнего мира, великая библиотека в Александрии стала центром научных достижений. Пишется, что в библиотеке было более 500 000 свитков [15, с.59]. Около 235 г. до н.э. Эратосфен был назначен главным библиотекарем библиотеки в Александрии [1, с.388]. Именно в этот период Эратосфен изобрел свой метод аппроксимации окружности Земли.

Все работы, победившие в студенческом конкурсе HOM SIGMAA, публикуются в Convergence ; многие также доступны в архивах HOM SIGMAA по адресу http://homsigmaa.net/writing-prizes/.

Другие студенческие конкурсные работы HOM SIGMAA в Convergence

2020: Джеффри Пауэрс (Общественный колледж Гранд-Рапидс), «Вычислил ли Архимед вычисления?»

2019: Аманда Нетингтон (Университет Миссури, Канзас-Сити), «Достижение философского совершенства: успешная замена постулата Евклида Омаром Хайямом».

2018: Первое место – Калли Лейн (Университет Миссури – Канзас-Сити), «Гонка к преломлению: повторное открытие закона Снелла»; Второе место – Кристен Питерс (Университет Ли) «Реальность комплекса: открытие и развитие мнимых чисел» и Рэйчел Талмадж (Университет Миссури – Канзас-Сити) «Франсуа Виет использует геометрию для решения трех задач».

2017: Со-победители – Аманда Акин (Университет Ли), «В бесконечность и дальше: историческое путешествие в созерцании бесконечности», Иоганн Геблер (Гарвардский университет), «Традиционализм: 1894–1925» и Натан Оттен (Университет Миссури — Канзас-Сити), «Гюйгенс и : ценность всех шансов в играх удачи».

2016: Со-победители – Бриттани Энн Карлсон (Общественный колледж Солт-Лейк-Сити), «Скрытый элемент деятельности Алисы в стране чудес: консервативная викторианская математика», и Уильям Коул (Университет Ли), «Эволюция круга». Метод в аддитивной теории простых чисел».

2015: Со-победители — Сэмюэл Паттерсон (Университет Миссури, Канзас-Сити), «Бернард Больцано, незамеченный в свое время гений», и Бриана Янки (Университет Ли), «Исследование опровергнутых математических идей через призму Философия».

2014: Первое место – Дженна Миллер (Университет Миссури – Канзас-Сити), «Проливая свет на статистическую жизнь Флоренс Найтингейл», и Анна Рифф (Университет Миссури – Канзас-Сити), «Невозможное доказательство: Анализ попыток Адриана-Мари Лежандра доказать пятый постулат Евклида»; Второе место – Пол Айерс (Университет Миссури – Канзас-Сити), « Габриэль Крамер: Более 260 лет сокрушения неизвестных », и Мэри Рафф (Университет штата Колорадо, Пуэбло), «Вероятность до 1750». : A Creative Perspective».

2012: Первое место – Джесси Хамер (Университет Миссури – Канзас-Сити), «Неделимые и циклоиды в начале 17 века»; Второе место – Кевин Л. Винингер (Университет Оттербейна), «Об основах рентгеновской компьютерной томографии в медицине: фундаментальный обзор« преобразования Радона »и дань уважения Иоганну Радону».

2011: Первое место – Пол Шталь (Университет Миссури – Канзас-Сити), «Развитие математической астрономии Кеплером»; Второе место – Сара Кострелл (Университет Брандейса), «Математика и математическая мысль в квадривиуме Исидора Севильского» и Рик Хилл (Университет Миссури – Канзас-Сити), « Artis Analyticae Praxis Томаса Хэрриота и корни современной алгебры». ».

2010: Со-победители – Дженнифер Нильсен (Университет Миссури – Канзас-Сити), «Сердце – это пыльная доска: Абу’л Вафа Аль-Бузджани, Препарирование, строительство и диалог между искусством и математикой в ​​средневековье» Исламская культура», Палмер Рэмпелл (Академия Филлипса и Гарвардский университет), «Использование подобия в древневавилонской математике», и Стефани Стрек (Тихоокеанский лютеранский университет), «Проблема Ферма».

2009: Первое место – Натан Маклафлин (Университет Монтаны), «Математическая оптика сэра Уильяма Гамильтона: коническое преломление и кватернионы»; Второе место – Тим Чалберг (Тихоокеанский лютеранский университет), «Регрессионный анализ: мощный инструмент и захватывающая драма»; Почетное упоминание – Эми Бухманн (Университет Чепмена), «Краткая история кватернионов и теория голоморфных функций кватернионных переменных».

2008: Первое место – Мейм Мэлони (Чикагский университет), «Конструктивизм: реалистичный подход к математике?»; Второе место – Вуди Берчетт (Джорджтаунский колледж), «Нестандартное мышление: геометрическая интерпретация квадратичных задач в BM 139».01» и Коул МакГи (Университет штата Колорадо, Пуэбло), «Жан Ле Ронд Д’Аламбер: биография математика, философа и литератора»; Почетное упоминание – Мейм Мэлони (Чикагский университет), «Патологические функции в 18-м и 19-м веках».

2007: Со-победители — Рори Плант, « Libra Astronomica и его математика», и Дуглас Смит (Университет Майами, Огайо), «Теорема Лукаса: великая теорема».

2006: Со-победители – Дженнифер Вигерт, «Проницательность кругов: история изопериметрической проблемы», и Саманта Рейнольдс (Университет Миссури, Канзас-Сити), «Мария Гаэтана Аньези: женщина-математик и блестящий толкователь 18 ^-й век.

2005: Первое место – Newlyn Walkup (Университет Миссури – Канзас-Сити), «Эратосфен и тайна стадиона»; Второе место – Джеймс Коллингвуд (Университет Дрейка), «Строгость анализа: от Ньютона до Коши».