Краткие изложения 1и 2 главы «Дубровский» — Спрашивалка

СС

Сергей Сирица

Глава1. “Несколько лет тому назад в одном из своих поместий жил старинный русский барин, Кирила Петрович Троекуров. Его богатство, знатный род и связи давали ему большой вес в губерниях, где находилось его имение”. Дом его был полон гостями, готовыми разделять его шумные, а порой и буйные увеселения. Со своими крестьянами он был строг до жестокости. Приятелей у него не было, кроме Андрея Гавриловича Дубровского. Этот Дубровский был ближайший сосед Троекурова, отставной военный, владеющий семьюдесятью душами. Став соседями, они съезжались каждый день. Многое в их судьбах было похожим: женившись по любви, они вскоре овдовели, имели детей. Сын Дубровского, Владимир, воспитывался в Петербурге, Маша Троекурова “росла в, глазах родителя”. Троекуров часто говаривал, что отдаст свою дочь за Володьку, если тот будет путевым человеком, но Андрей Гаврилович возражал: бедному дворянину лучше жениться на ровне, “чем сделаться приказчиком избалованной бабенки”.

Дубровский всегда смело высказывал свое мнение, не оглядываясь на Троекурова. Ему это сходило с рук. Если кто-то пробовал ему подражать, Троекуров быстро ставил на место зарвавшегося смельчака. Дубровский один оставался “вне общего закона”. “Нечаянный случай все расстроил и переменил”. Раз осенью, готовясь к охоте, Троекуров с гостями пошел на псарню, которая была прекрасно организована. Один из псарей обиженно ответил: на свое житье не жалуемся, а вот иному дворянину не мешало бы променять свою усадьбу на местную конуру. “Ему было б и сытнее и теплее”. Троекуров громко рассмеялся на дервость своего псаря, Дубровский побледнел и промолчал. Сев за стол, Троекуров хватился Дубровского, послал своих людей за ним. “Отроду не выезжал он на охоту без Дубровского… ”. Но сосед не вернулся, вторично послали человека, он привез записку, в которой Дубровский требовал прислать к нему дерзкого псаря, а уж он сам решит: “наказать его или помиловать”. А сносить дерзости от кого бы то ни было он не намерен, так как является старинным дворянином. Письмо Дубровского рассердило Троекурова. Охота состоялась без Дубровского и была неудачна. Троекуров сердился на всех подряд, однако Дубровский так и не появлялся в Покровском. Кирила Петрович скучал, злился, высказывал самые оскорбительные выражения о своем бывшем приятеле, которые с удовольствием доносились до адресата соседями. Новое обстоятельство уничтожило последнюю надежду на примирение: Дубровский поймал в своей роще порубщиков-мужиков Троекурова. До этого троекуровские мужики не позволяли себе “шалить в пределах его владений”, зная о дружеских отношениях между господами. Теперь же они воспользовались размолвкой приятелей. Дубровский наказал мужиков прутьями, а их лошадей взял в работы. Троекуров был взбешен самовольством Дубровского, решил отнять имение Дубровского. Для этого случая был призван заседатель Шабашкин. Троекуров высказал желание “безо всякого права отнять имение” соседа, Шабашкин обрадовался, узнав, что все документы на имение сгорели при пожаре. Это заметно облегчало дело, кроме того, Дубровский мало смыслил в делах, был горяч и полагался на закон. Троекуров доверился Шабашкину, который занимался подкупом судей, всяко толковал закон и добился рассмотрения дела в суде.
Глава2.Приехавший в суд Дубровский почти не обратил на себя внимания, Троекуров же был встречен с подобострастием. Судом было установлено, что Дубровский владеет Кистеневкой незаконно, и имение должно быть передано законному владельцу — Троекурову. Дубровскому же предлагается подать апелляцию, если он не согласен с решением суда. Дубровский поднял голову, глаза его горели, схватив чернильницу, он пустил ею в председателя суда; разбушевавшегося помещика едва уняли сбежавшиеся сторожа. Затем больной Дубровский был отвезен в Кистеневку, “почти уже ему не принадлежащую”. Внезапное сумасшествие Дубровского сильно подействовало на Троекурова, отравив ему торжество победы.

Краткое содержание книги Дубровский по главам (Пушкин) за 2 минуты пересказ сюжета

• Краткие содержания
• Пушкин
• Дубровский по главам

Глава 1

В селе Покровском, в своём имении жил богатый помещик Кирилл Петрович Троекуров. Вся его жизнь проходила в кутежах и проказах. Крепостные крестьяне боялись его и, в то же время, гордились богатством своего барина. Соседи Кирилла Петровича старались ему во всём угодить.

У помещика был единственный друг, которого он уважал и с которым поддерживал отношения с молодости. Это был Дубровский Андрей Гаврилович, живший недалеко от Покровского в своём небольшом имении. Друзья были вдовцами и имели детей. У Троекурова была семнадцатилетняя дочь Маша и сын Саша, которого родила помещику гувернантка, у Дубровского – сын, которого звали Владимиром.

Несмотря на дружбу, Дубровский часто высказывал Троекурову своё негативное мнение в отношении жизни его крепостных. Однажды к Троекурову приехали гости, и он с гордостью показывал им свою псарню. Дубровский и здесь не смог промолчать. Он напомнил Кириллу Петровичу о том, как плохо живут в его имении слуги.

За охотничьими собаками следили специально обученные люди. Один из них, оскорбившись, сказал Дубровскому, что есть помещики, которым, не мешало бы, обменять их нищенское существование на конуру в псарне хозяина. Андрей Гаврилович, не сказав ни слова, развернулся и уехал домой. Вскоре Троекуров получил от него письмо, в котором тот требовал наказать наглого слугу. В тот же день крестьянами Дубровского были пойманы мужики из имения Троекурова, которые рубили чужой лес. Андрей Гаврилович приказал забрать у них лошадей, а самих воров высечь на конюшне.

Троекуров решил отомстить Дубровскому за самоуправство. Он подкупил судебного заседателя Шабашкина, чтобы тот помог ему отобрать у Андрея Гавриловича его единственное имение.

Глава 2

Документы Дубровского на владение Кистенёвкой были уничтожены во время пожара, поэтому он не смог доказать, что имение принадлежит ему по закону. Заручившись поддержкой продажного заседателя, Троекуров выиграл этот суд, и имение перешло к нему. Когда Андрею Гавриловичу предложили подписать решение суда, с ним случился нервный срыв. Дубровского отвезли в родной дом, который у него отобрали.

Глава 3

Андрею Гавриловичу с каждым днём становилось всё хуже. За ним присматривала старая нянька Егоровна.

Сын Дубровского Владимир только недавно окончил Кадетский корпус и получил звание корнета. Отец старался, чтобы сын ни в чём не нуждался, поэтому Владимир позволял себе проиграть в карты последние деньги или устроить весёлую пирушку. Он был хорош собой и мечтал жениться на богатой наследнице. Его нянька Егоровна сообщила своему воспитаннику о случившемся горе и о состоянии отца. Владимир с восьми лет учился в Петербурге, но всё равно любил отца и был сильно к нему привязан. Узнав о случившемся из письма Егоровны, он взял отпуск и через три дня уже был на своей станции.

Владимира встретил старый кучер Антон, который ждал его на станции четвёртый день. По дороге домой они разговорились, и кучер рассказал молодому барину о деревенских слухах. Подробностей он не знал. На крыльце Владимира встретила старая няня и повела его к отцу, который ждал его на пороге своей комнаты.

Глава 4

Андрей Гаврилович из-за своей болезни не сумел объяснить сыну суть дела. Сам Владимир не мог разобраться в нём, так как многих документов не хватало. В это время судебный заседатель прибыл в имение Троекурова, чтобы поздравить его с новым приобретением, так как срок апелляции уже прошёл. Но Кирилла Петровича мучила совесть, поэтому он был не в духе. В конце концов, он собрался и поехал к другу, чтобы помириться и вернуть ему Кистенёвку. Андрею Гавриловичу, который увидел в окно подъезжающего Троекурова, стало плохо. Испуганный Владимир послал слугу за врачом, а Троекурова приказал гнать со двора. Вскоре старый барин умер.

Глава 5

Похоронили Дубровского на старом кладбище рядом со своей женой. Егоровна пригласила попа и церковный причет на поминальный обед. Владимир Дубровский на нём отсутствовал. Он скрылся в берёзовой роще и долго думал о своей дальнейшей судьбе. Вернулся он в имение поздним вечером и узнал, что в доме его ждут судебные чиновники. Вместе с ними прибыл и заседатель Шабашкин. Он сообщил крестьянам, что имение является собственностью Троекурова.

Время было позднее, поэтому чиновники остались ночевать в доме. В это время Владимир долго успокаивал крестьян, собравшихся во дворе.

Глава 6

До поздней ночи Владимир разбирал бумаги отца. Среди них он нашёл письма матери к отцу во время Турецкой кампании и долго читал их. Потом он спрятал письма в карман и вышел из дома. Владимир приказал вывести из барской усадьбы своих людей. Остались только пьяные судебные чиновники, спящие на полу. Владимир приказал принести соломы и обложить ею дом. Перед тем, как поднести огонь к куче соломы, он послал кузнеца Архипа проверить, не закрыл ли он случайно входную дверь. Кузнец попробовал – дверь была открыта. Перекрестившись, Архип закрыл её на ключ и выскочил во двор.

Владимир сел на телегу вместе с няней и её сыном Гришкой и выехал со двора. В это время огонь охватил здание. Из него были слышны вопли чиновников, но крыша обвалилась, и крики затихли.

Глава 7

После пожара в Кистенёвке сам Троекуров пытался найти виновника. Шли слухи, что это сделал кузнец Архип. Но найти его не смогли. Вскоре в округе появилась шайка разбойников, которая грабила и сжигала богатые имения. Поговаривали, что предводителем этой шайки был Владимир Дубровский. Только усадьбу Троекурова разбойники обходили стороной. Кирилл Петрович на званых вечерах хвалился, что разбойники сами боятся его.

Глава 8

Дочь Троекурова Маша росла без матери. Кирилл Петрович очень любил дочь, но она избегала его общества. Часто её можно было увидеть в библиотеке. Её образованием пыталась заниматься гувернантка Мими, к которой был не равнодушен сам Троекуров. Вскоре эта симпатия стала явной. Мими родила мальчика, в котором он признал своего сына. Хотя таких мальчиков, очень похожих лицом на своего барина, можно было немало встретить и в деревне, и во дворе имения.

Саше исполнилось девять лет. Для него Троекуров выписал из столицы учителя-француза. Вскоре он явился в Покровское и предоставил ему свои рекомендации. Барину понравилось его спокойное открытое лицо.

Однажды по приказу Троекурова слуги втолкнули учителя в комнату, где на цепи сидел голодный медведь. Молодой человек спокойно достал из кармана пистолет и пристрелил животное. После этого случая в доме все стали уважать его. Троекуров хвалился его бесстрашием перед своими гостями. Маше учитель давал уроки музыки.

Том 2

Глава 9

На праздник в имение Кирилла Петровича съехались гости. Последним явился Спицын Антон Пафнутьевич. Он был сильно напуган, так как очень боялся разбойников. За праздничным столом исправник зачитал приметы Дубровского, но Троекуров высмеял его, так как под такое описание мог попасть любой молодой мужчина. Небогатая помещица Анна Савишна заявила, что лично видела Дубровского и считает его справедливым человеком. Когда он узнал, кому предназначены деньги, он не взял из них ни копейки.

Глава 10

Услышав, как помещик расхваливает своего учителя-француза, Антон Пафнутьевич напросился к нему во флигель переночевать. В ту же ночь француз, который на самом деле был Дубровским, забрал у Спицына все его деньги. Тот прятал их на груди в кожаном мешочке.

Глава 11

С настоящим учителем-французом Дубровский встретился на станции и предложил ему большую сумму денег взамен на его документы. Дефорж согласился, так как ехать в провинцию ему не хотелось.

Дубровский поселился в доме Троекурова. Все полюбили молодого человека за смелость, доброту и внимание.

Глава 12

Владимир рассказал Маше о своей судьбе и признался ей в любви. Он обещал прийти ей на помощь, если вдруг она ей понадобится. В этот же день в имении Троекурова появился исправник. Он приехал арестовать француза, так как он и был Дубровским. Но молодого учителя не смогли найти.

Глава 13

В конце весны в поместье Арбатовом появился его хозяин – князь Верейский. Он стал частым гостем в имении Троекурова и много внимания уделял Маше, восхищаясь её красотой. Ему было пятьдесят лет, и он был интересным собеседником, так как много путешествовал.

Глава 14

Троекуров дал согласие на брак Маши с князем Верейским, не считаясь с чувствами и желаниями дочери. В этот же день девушка получила письмо от Дубровского, где он просил её о встрече в назначенном месте.

Глава 15

Дубровский встретился с Машей, чтобы предложить ей свою помощь. Он уже знал о сватовстве престарелого князя. Девушка попросила дать ей время – может, ей удастся уговорить отца. Расставаясь, Дубровский оставил девушке кольцо. Если ей понадобится помощь, она должна положить кольцо в дупло старого дуба. И тогда он будет знать, что ей нужна его помощь.

Глава 16

Маша послала письмо князю Верейскому, в котором просила его отказаться от этого брака, так как не испытывала к нему никаких чувств. Князь приехал к Кириллу Петровичу и показал ему письмо девушки. Рассерженный отец приказал запереть Машу в её комнате и ускорить приготовления к свадьбе.

Глава 17

Маша попросила брата, чтобы он положил её кольцо в дупло старого дуба. Когда Саша выполнил просьбу сестры и собрался вернуться домой, возле дуба появился деревенский мальчишка. На крик Саши прибежали слуги и схватили незнакомого мальчика. Допрашивал его сам Троекуров, но ничего добиться от него не смог. Пришлось мальчика отпустить.

Глава 18

Всю дорогу до церкви Маша с нетерпением ждала помощи, но Владимир не появлялся. После венчания карету остановили разбойники во главе с Дубровским. Но Маша отказалась ехать с ним, так как он опоздал, и теперь она жена князя Верейского. Во время этого разговора князь ранил Владимира, и его увели его люди.

Глава 19

На лагерь разбойников напали солдаты. Дубровский и его люди храбро отражали их атаки. Но силы их были неравны. Дубровский жалел своих преданных товарищей, поэтому распустил шайку. Куда он делся, никто не знал, но грабежи и пожары прекратились. Прошёл слух, что Владимир Дубровский покинул Россию.

Чему учит роман

Произведение учит справедливости, чувству собственного достоинства, благородству.

Можете использовать этот текст для читательского дневника

Пушкин. Все произведения

• Арап Петра Великого
• Барышня-крестьянка
• Бахчисарайский фонтан
• Борис Годунов
• Братья разбойники
• Выстрел
• Гаврилиада
• Граф Нулин
• Гробовщик
• Домик в Коломне
• Дубровский
• Дубровский по главам
• Евгений Онегин
• Евгений Онегин по главам
• Жених
• История Пугачёва
• Кавказский пленник
• Каменный гость
• Капитанская дочка
• Кирджали
• Маленькие трагедии
• Медведиха
• Медный всадник
• Метель
• Моцарт и Сальери
• Песнь о Вещем Олеге
• Пиковая дама
• Пиковая дама по главам
• Пир во время чумы
• Повести Белкина
• Полтава
• Русалка
• Руслан и Людмила
• Сказка о золотом петушке
• Сказка о мертвой царевне и о семи богатырях
• Сказка о попе и его работнике Балде
• Сказка о рыбаке и рыбке
• Сказка о царе Салтане
• Скупой рыцарь
• Станционный смотритель
• У Лукоморья дуб зелёный
• Цыганы

Сочинение: Образ отца Дубровского в романе «Дубровский» (А.

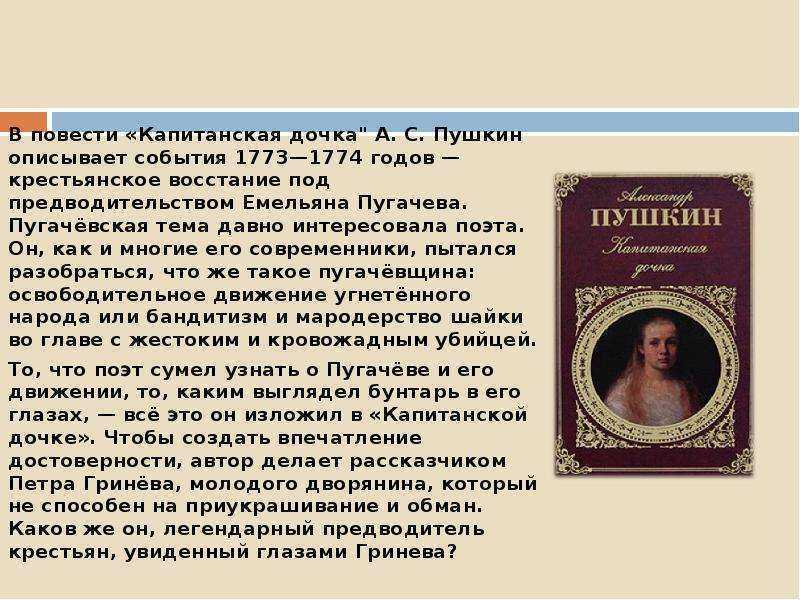С. Пушкин)

(466 слов) В романе «Дубровский» главным героем становится сын Андрея Гавриловича – Владимир Дубровский. Но события жизни отца, его решения и поступки послужили отправной точкой в судьбе главного героя. Фигура старшего Дубровского очень важна для понимания романа.

Андрей Гаврилович – единственный, кто в сложных взаимоотношениях с Троекуровым не боится потерять его расположения. Он боится потерять себя и свои представления о чести и уважении, что характеризует его как человека принципиального, не способного пойти на сделку с совестью или отклониться от собственных убеждений. С первых строк читатель узнаёт об особенном положении отца Дубровского. В молодости он служил вместе с Троекуровым, и последний ценит его дружбу, уважает мнение. Дубровский — единственный человек в окружении Кирилла Петровича, кто смеет высказывать своё подлинное мнение, даже если оно идёт в разрез с мнением Троекурова.

Андрей Гаврилович рано потерял жену, сын уже взрослый, и одним из немногих развлечений для него становится охота с Троекуровым. Но он не побоится потерять это развлечение. Старший Дубровский относится к себе уважительно, и потому искренне оскорбляется, когда слуга отвечает ему, не соблюдая субординацию, нарушая все правила. Старший Дубровский оскорбился в большей степени тем, что хозяин дома – его друг – никак не вмешался и не принёс извинений за поведение слуги. Глубоко обиженный поведением Кирилла Петровича и его слуги, Андрей Гаврилович незамедлительно уезжает, прерывая любые отношения до того момента, как будут принесены извинения. К сожалению, этому не суждено было произойти. Отсутствие Андрея Гавриловича было замечено Троекуровым не сразу, но, когда он разобрался в сути вопроса, стало понятно, что на примирение он идти не хочет.

Когда старший Дубровский узнаёт о желании Троекурова забрать его имение, он не придаёт делу должного внимания. Но не только потому, что не может или не знает, каким образом лучше поступить. Просто он не верит в бесчестность. Он уверен, что выиграет дело, так как правда на его стороне. Так как сам Андрей Гаврилович никогда не поступил бы подобным образом, ему бы просто не пришло в голову пытаться отобрать имение нечестным путём, он не может представить, что его могут обмануть. Именно из-за этой веры в невозможность такого масштабного обмана, Дубровский теряет имение. И не только усадьбу и землю, но и собственную жизнь. Он не пережил таких больших потрясений, и умер на руках сына.

Пушкин в образах Троекурова и Дубровского даёт нам портрет людей того времени: один заносчивый и ограниченный человек (назвать его злым трудно, так как он одумался и хотел примириться, но не успел) – Троекуров, который владеет обществом. И довольствующийся своим положением, уважающий собственные принципы, Андрей Дубровский. Во многом это герои-антагонисты, но между ними есть нечто общее: они одинаково любят своих детей, у них общее прошлое, и некоторые интересы их совпадают.

Однако образ Андрея Гавриловича Дубровского – это образ человека принципиального, твёрдого в своих решениях, и не способного пойти на обман. Главным ударом для него стал не столько факт потери имения, но сама возможность этой потери. Ведь он был уверен, что правда всегда защит его.

Автор: Таисия Ишниазова

Сценка «Отказ Маши выходить замуж за князя Верейского», Подведение итогов.

Когда дочитываешь последние страницы повести, охватывает целая буря самых разнообразных чувств. Прежде всего, удивляешься, что повествование окончилось так внезапно, и мы совершенно не знаем, как сложилась дальше жизнь главного героя. Такое впечатление, что Пушкин просто отложил рукопись в сторону, сказав то главное, что хотел сказать нам. Повесть действительно считалась неоконченной и не имела названия, именем главного героя произведение назвали, готовя к посмертному изданию сочинения Пушкина (при жизни поэта повесть не была напечатана).

Подумайте, как могла бы сложиться дальнейшая судьба героев.

Урок по литературе на тему «Отец и сын Дубровские» ( 6 класс)

Конспект урока по литературе 6 класс

Тема: «Отец и сын Дубровские»

Дата:

Тип урока:

изучение нового материала

Цели урока

:

— продолжить работу над романом, вникнуть в суть взаимоотношений между героями;

— раскрыть характер Владимира Дубровского.

Планируемые результаты образования:

Предметные:

умение выразительно читать и анализировать произведение, определение центральной проблемы романа, проявляющейся в столкновении независимой личности с произволом, деспотизмом, беззаконием, опирающимся на богатство, всевластие; показать духовную преемственность отца и сына Дубровских;

Личностные:

формирование положительного отношения и интереса к урокам литературы,опыт оценки своих эмоциональных реакций на прочитанное произведение, формирование нравственно-эстетические представления учащихся в ходе выявления значений понятий «честность», «своеволие», «духовный», «преемник».

Метапредметные:

Познавательные: учатся анализировать, обобщать факты, выявлять причины и следствия простых явлений

Регулятивные: умение планировать свои действия в соответствии с поставленной задачей и условиями ее реализации

Коммуникативные: умение строить монологическое высказывание на заданную тему.

Оборудование:

учебник-хрестоматия; компьютер, проектор; презентация; карточки; словари.

Методы

: аналитическая беседа, работа с книгой, анализ эпизода, устное рисование, выразительное чтение, словарная работа, рассказ учителя.

Формы:

коллективная, частично индивидуальная.

Ход урока

1.
Организационный момент.
2.
Актуализация знаний
Проверка домашнего задания. Конкурс на лучшее название второй, третьей и четвёртой глав романа.

3.
Выявление места и причины затруднения.
Как в суде принимают Дубровского и Троекурова? Найдите в тексте слова, характеризующие отношение писарей к бывшим друзьям, и заполните таблицу.

Отношение присутствующих в суде
К Дубровскому	К Троекурову
«Никто не обратил на него внимания», «Андрей Гаврилович стоя прислонился к стенке».	«Писаря встали, встретили его с изъявлениями глубокого подобострастия, придвинули ему кресла из уважения к его чину, летам и дородности, заседатель встал и с низким поклоном обратился к Троекурову».

Как вы думаете, какова тема нашего урока, каковы наши цели.

Учащиеся формулируют тему урока.

4. Изучение нового материала.

4.I. Анализ II главы романа.

Зачем Троекурову нужен был суд?

Ему не нужна деревня Дубровского,

для него главным было желание сломить гордость и независимость А.Г. Дубровского.

4.2. Как встретили члены суда А.Г. Дубровского и К.П. Троекурова?

При появлении Дубровского «никто не обратил на него внимания». Он «стоя прислонился к стенке». Когда же приехал Троекуров, «писаря встали и заложили перья за ухо. Члены встретили его с изъявлениями глубокого подобострастия, подвинули ему кресло из уважения к его чину, летам и дородности».

4.3. Как вели себя чиновники после оглашения решения суда?

«Заседатель встал и с низким поклоном обратился к Троекурову, приглашая его подписать предлагаемую бумагу»; Троекуров вышел, «сопровождаемый всем судом»; «Секретарь поднес ему [Дубровскому] бумагу».

4.4.
Как вели себя герои?
«Торжествующий Троекуров… подписал под решением суда совершенное свое удовольствие»; «Дубровский стал неподвижен, потупя голову». Несправедливое решение суда привело А. Г. Дубровского к внезапному сумасшествию.

4.5.
Как ты понимаешь выражение:
«Внезапное сумасшествие Дубровскогосильно подействовало на его воображение и отравило его торжество»? В Троекурове проснулся человек, обнаружилась совесть.

Отец и сын Дубровские

Жизнь Владимира Дубровского в Петербурге:

Владимир считался одним из лучших офицеров. Его любили за честность и независимость. Владимир вел в Петербурге жизнь, по его мнению, приличную гвардейскому офицеру. Отец посылал ему деньги, себе не оставляя почти ничего, и Дубровский, расточительный и честолюбивый молодой человек, «позволял себе роскошные прихоти, играл в карты и входил в долги, не заботясь о будущем». Он надеялся на отца и на то, что сможет найти себе богатую невесту.

Отношения отца и сына:

Владимир лишился матери с малолетства и, почти не зная отца своего, был привезен в Петербург на восьмом году своего возраста; со всем тем, он романтически был к нему привязан и тем более любил семейственную жизнь, чем менее успел насладиться ее тихими радостями.

Как воспринял Владимир известие о болезни отца?

Любовь и сила привязанности к отцу заставляют его отказаться от беспечной жизни и ехать в Кистеневку. Известие о болезни отца Дубровский воспринял «с необыкновенным волнением». Его ужасало положение отца, и он «упрекал себя в преступном небрежении». В характере Дубровского проявились любовь к своей семье и готовность прийти на помощь отцу.

Отношение крепостных крестьян к Троекурову и Дубровскому

Обратимся к I главе, где сказано: «Троекуров с крепостными и дворовыми обходился… строго и своенравно, но они тщеславились богатством и славою своего господина и в свою очередь позволяли себе много в отношении к их соседям, надеясь на его сильное покровительство. Поэтому становится ясно, что прав Антон, который на вопрос Владимира Дубровского: «Стало быть, вы не желаете перейти во владение Троекурову?» — отвечает: «Господи, упаси и избавь: у него часом и своим плохо приходится, а достанутся чужие, так он с них не только шкуру, да и мясо-то отдерет».

Совершенно по-другому относятся крестьяне к отцу и сыну Дубровским: «Не надо нам никого, кроме тебя, наш кормилец. Не выдавай ты нас, а мы уж за тебя станем». К крепостным крестьянам Дубровские относятся по-человечески, не презирают их и не грабят. Крестьяне понимали, какая участь ждет их, если они окажутся у Троекурова, поэтому молодой Дубровский находит сочувствие и поддержку у своих крепостных.

Вывод:

стремление жить, соблюдая законы чести, не завися от своеволия сильных мира сего, присущи отцу и сыну Дубровским. По этой причине они оба находятся в положении «вне общего закона», пытаясь противостоять несправедливости.

Андрею Гавриловичу не удалось что-либо изменить. Владимир Дубровский- духовный наследник отца, полный чувства дворянской ответственности за судьбу народа, вступает на путь противостояния злу.

5.
Физкультминутка
6.
Закрепление изученного материала.
6.1. Лексическая работа.

Подберите синонимы к слову своеволие. (Самодурство, своевластность, упрямство).

Назовите понятия, противоположные по смыслу слову честность. (Обман, ложь, лицемерие).

Каким героям романа присущи эти качества? (Троекурову и его приспешникам, которые во всем потакают самодурству барина).

Почему крестьяне Кистеневки отзывчивы, верны, решительны и участливы, наделены чувством человеческого достоинства, а люди Троекурова «известные разбойники»? (Крестьяне во многом походят на помещика, которому принадлежат. Человеческие качества людей Дубровского отражают искренность, независимость и справедливость семьи Дубровских. Крепостным Троекурова присуща наглость – следствие своеволия их барина).

7.
Самоконтроль
.

Найдите в тексте цитаты, свидетельствующие о подлинной преданности Владимира Дубровского отцу.

8.

8.1.Выразительное чтение эпизода от слов «Дубровский поднял голову…» до слов «… на котором паслась запутанная лошадь».

8.2. Анализ эпизодов, свидетельствующих об отношении Дубровских к крестьянам, о многоплановости народного характера.

— Каковы крепостные крестьяне Дубровских?

8.3. Выразительное чтение письма Орины Егоровны Бузырёвой.

— Как раскрывается характер героини в письме?

8.4. Выразительное чтение по ролям диалога кучера Антона и Владимира Дубровского.

— Как относится к событиям кучер Антон? Какие черты народного характера раскрываются автором в образе Антона?

— Зачем автор вводит в речь Антона пословицы: «Плетью обуха не перешибёшь», «Было бы корыто, а свиньи-то найдутся», «На чужой рот пуговицы не нашьешь»? Как, судя по пословицам, простые люди отнеслись к ссоре господ?

— Почему крестьяне Кистеневки отзывчивы, верны, решительны и участливы, наделены чувством человеческого достоинства, а люди Троекурова — «известные разбойники»?

9. Рефлексия. Подведение итогов.

10. Домашнее задание:

Дать название главам V—XI.

Составить цитатный план

главы VI.

Групповое задание.

Выписать из текста эпизода«Дубровский в Кистеневской

роще» цитаты, характеризующие состояние героя. Подготовить чтение по ролям.

А. С. Пушкин «Дубровский». Изображение русского барства. Конфликт Дубровского и Троекурова.

Тема:

А. С. Пушкин «Дубровский». Изображение русского барства. Конфликт Дубровского и Троекурова.

Цели урока

: 1)выработать навыки работы с текстом произведения большого объема с помощью предварительно объявленных вопросов; 2) развивать умение выделять главную мысль, делать выводы, сопоставляя описанные события с историей; 3) совершенствовать навыки составления плана текста, навыки текстологического анализа произведения; 4) работать над выразительным чтением; 5) воспитывать культуру связной речи; 6) совершенствовать умение выражать свое мнение.

Ход урока:

1. Слово учителя

После «Повестей Белкина», в октябре 1832 года, А. С. Пушкин принялся за роман в трех частях, который остался незаконченным и был напечатан только после его смерти. Это был «Дубровский», названный так по имени главного героя. В рукописи заглавия нет, на первом листе просто сказано: «Том первый. Глава первая». Пушкиным были написаны только два тома. Как показывают отметки в рукописи, второй том был закончен в феврале 1833 года. В основу романа Пушкин положил случай, довольно характерный для отношений между помещиками и для судебного произвола, существовавшего в то время. Пользуясь своим влиянием, сильный и богатый помещик всегда мог притеснить бедного соседа и даже отнять у него законно принадлежащее ему имение.

Об одном таком случае рассказал Пушкину его приятель В. П. Нащокин, знавший некоего помещика Островского, который был разорен своим знатным соседом, лишился имения и вместе со своими крестьянами организовал разбойничью шайку. Писатель заботился о реалистической правдивости своего романа, о приближении его к подлинной действительности.

Решения дробных уравнений Конопельченко-Дубровского и Нижника-Новикова-Веселова с помощью обобщенного метода дробных подуравнений

На этой странице

АннотацияВведениеЗаключениеСсылкиАвторское правоСтатьи по теме

Предлагается новый обобщенный метод дробных подуравнений, основанный на связи дробно-связанных уравнений. Этот метод применяется к пространственно-временным дробно-связанным уравнениям Конопельченко-Дубровского и уравнениям Нижника-Новикова-Веселова. В результате получается много точных решений, включая решения гиперболических функций, решения тригонометрических функций и рациональные решения. Отмечается, что предлагаемый подход обеспечивает простой и надежный инструмент для решения многих других дифференциальных уравнений с дробной связью.

1. Введение

Дробное исчисление является одним из обобщений обычного исчисления. Вообще говоря, есть два вида дробных производных. Одним из них является нелокальная дробная производная [1, 2], то есть производная Капуто и производная Римана-Лиувилля, которые успешно используются в различных областях науки и техники. Другой — локальная дробная производная, то есть производная Колванкара-Гангала (K-G) [3, 4], фрактальная производная Чена [5, 6], производная Крессона [7] и модифицированная производная Римана-Лиувилля Жюмари [8] . В то же время дробные дифференциальные уравнения привлекают большое внимание в различных прикладных науках. Однако у нас возникают трудности с нахождением точных аналитических решений [9].–12] дифференциальных уравнений дробного порядка, которые все чаще появляются в различных областях исследований и технических приложениях. Таким образом, для решения этих уравнений использовались численные методы, а также некоторые полуаналитические методы [13–16].

На основе принципа однородного баланса [17], модифицированной производной Римана-Лиувилля Джумари [8] и символьных вычислений С. Чжан и Х.-К. Чжан предложил метод дробного подуравнения для поиска явных решений ФДУ. Используя этот метод, С. Чжан и Х.-К. Чжан успешно получил некоторые точные решения пространственно-временной дробной модели биологической популяции и дробного уравнения Фокаса [18]. Джафари и др. дали некоторые решения дробных уравнений Кана-Хиллиарда и Клейна-Гордона [19].]. Танг и др. В [20] предложен обобщенный метод дробных подуравнений для дробных дифференциальных уравнений с переменными коэффициентами. Гуо и др. [21] и Чжао и соавт. [22] улучшили дробное подуравнение и применили его к дифференциальным уравнениям с дробной связью в пространстве-времени; в своей статье они выбирают два или три подходящих анзаца. Однако для некоторых связанных уравнений [23, 24], даже для некоторых уравнений с дробной связью, мы можем получить связь функций. Итак, мы предлагаем новое обобщенное дробное подуравнение, которое выбирает только один подходящий анзац, и используем этот метод для решения следующих двух NFDE.

(1) Пространственно-временные дробно-связанные уравнения Конопельченко-Дубровского (КД) в виде которое является преобразованным обобщением уравнений КД [25], где и – вещественные константы. Уравнение (1) представляет собой дробное эволюционное уравнение в двух пространственных измерениях и одном временном, где и – текущие координаты, – время, и – амплитуды соответствующих волн. и представляют собой модифицированную Жюмари производную Римана-Лиувилля порядка, определенного в разделе 2, . Модифицированная производная Джумари Римана-Лиувилля обладает многими интересными свойствами. Уравнения КД можно использовать для описания динамики океана, гидромеханики и физики плазмы, а уравнения Гарднера, КП, модифицированные КП и уравнения КД являются частными случаями уравнения (1). При , , (1) – уравнение Гарднера (объединенное КдФ и модифицированное уравнение). При , , (1) – известное уравнение Кадомцева-Петвиашвили (КП), а модифицированное уравнение КП читается из (1) при , .

(2) Пространственно-временное уравнение с дробной связью Нижника-Новикова-Веселова (ННВ) в виде где , и – заданные константы, удовлетворяющие , и , , и – функции от , случай, когда был изучен в [26].

Уравнения NNV изучались в нескольких областях физики, включая физику конденсированного состояния, гидромеханику, физику плазмы и оптику.

Остальная часть этого документа организована следующим образом. В разделе 2 даны некоторые основные определения модифицированной Джумари производной Римана-Лиувилля и основные этапы метода обобщенного дробного подуравнения. В разделе 3 мы строим точные решения вышеупомянутых пространственно-временных уравнений с дробной связью с помощью этого нового обобщенного метода. Некоторые выводы и обсуждения представлены в разделе 4.

2. Модифицированная производная Римана-Лиувилля Жюмари и метод обобщенного дробного подуравнения

Модифицированная производная Римана-Лиувилля [8] порядка дробной производной по времени определяется как

Некоторые свойства предложенной модифицированной производной Римана-Лиувилля перечислены в [8] следующим образом: Приведенные выше уравнения играют важную роль в дробном исчислении в следующих разделах.

мы предлагаем метод обобщенного дробного подуравнения; Основные этапы этого метода описаны ниже.

Шаг 1. Предположим, что NFDE с независимыми переменными заданы формулой где и — модифицированная производная Жюмари Римана-Лиувилля относительно и , — неизвестные функции, — полином от , и их различные частные производные, — многочлен от и их различные частные производные, а также производные высшего порядка и нелинейные члены вовлечены.

Шаг 2. Используя преобразования бегущей волны где – константа, которую необходимо определить позже, НОДУ (7) сводится к следующему нелинейному обыкновенному дифференциальному уравнению (ОДУ) дробного порядка для и :

Шаг 3. Для некоторых связанных уравнений получаем соотношение и подставляя в (8), имеем

Шаг 4. Предположим, что (12) имеет следующее решение: где – константы, которые будут определены позднее, – натуральное число, определяемое балансировкой производных высших порядков и нелинейных членов в (12) (подробности см.

в [17]), и удовлетворяет следующему дробному уравнению Риккати: Используя метод обобщенной Exp-функции через функции Миттаг-Леффлера, С. Чжан и Х.-К. Чжан впервые получил обобщенные гиперболические и тригонометрические функции дробного уравнения Риккати [18], а полученные пять решений (14) имеют вид где – обобщенные гиперболические и тригонометрические функции, определенные в [18] как где – функция Миттаг-Леффлера.

Шаг 5. Подставляя (13) в (12) вместе с (14) и используя свойства модифицированной Джумари производной Римана-Лиувилля (4)–(7), можно получить многочлен от . Обнуление всех коэффициентов дает набор переопределенных нелинейных алгебраических уравнений для , , .

Шаг 6. Воспользуйтесь известными решениями (14), чтобы получить решения рассматриваемых частично связанных NPDE.

3. Решения уравнения КД с дробной связью и уравнения ННС

В этом разделе мы применяем метод обобщенного дробного подуравнения для решения NPDE (1) и (2).

Пример 1. Дробные пространственно-временные уравнения КД. Рассматривая преобразования бегущей волны , (1) можно свести к следующим нелинейным дробным ОДУ: Из (18) и определения модифицированной Жюмари производной Римана-Лиувилля получаем где – произвольная постоянная. Подставляя (19) в (17), получаем Уравновешивая члены производных высшего порядка и нелинейные члены в (20), мы предполагаем, что (20) имеет следующее формальное решение: Подставляя (21) в (20) вместе с (14) и собирая коэффициенты и приравнивая их к нулю, мы можем получить систему алгебраических уравнений относительно , ​​, , , , , и . Решая алгебраические уравнения с помощью Mathematica, получаем следующее.

Дело 1. Есть

Случай 2. Один имеет

Случай 3. Один имеет

Случай 4. Один имеет

Дело 5. Есть

Случай 6. Один имеет

Случай 7. Один имеет

Случай 8. Один имеет
Используя случай 1, (21) и решения (14), мы можем найти следующие точные решения NFDE (1):
где , ,
где , , куда , , куда , , куда , . И ,  , , , и – произвольные константы.
Из случаев 2, 3, 4, 5, 6, 7 и 8 мы получаем множество других точных решений уравнения (1). Здесь мы опускаем их для простоты.
При , решения обобщенной гиперболической функции и решения обобщенной тригонометрической функции деградируют в решения гиперболической функции и решения тригонометрической функции. Подчеркнем, что при этом полученные точные решения, включая уединенные решения и рациональные решения, дают решения стандартного вида пространственно-временного дробного уравнения КД (1).

Пример 2 (пространственно-временные дробные уравнения NNV). Рассматривая преобразования бегущей волны , ,  и , (2) можно свести к следующим нелинейным дробным ОДУ: Из (36)-(37) и используя определение модифицированной Жюмари производной Римана-Лиувилля, получаем где и – произвольные константы. Подставляя (38) в (35), получаем Уравновешивая производные высшего порядка и нелинейные члены в (39), мы предполагаем, что (39) имеет следующее формальное решение: Подставляя (40) в (39) вместе с (14) и собирая коэффициенты и приравнивая их к нулю, мы можем получить набор алгебраических уравнений относительно , ​​, , , , , , , , и . Решая алгебраические уравнения с помощью Mathematica, мы имеем

Случай 1.

Случай 2. Один имеет

Случай 3. Один имеет
Используя случай 1, (40) и решения (14), мы можем найти следующие точные решения NFDE (2): куда , , куда , , куда , . куда , , куда , . И , , , и – произвольные константы, , , , и – обобщенные гиперболические и тригонометрические функции.
Из случаев 2 и 3 мы получаем много других точных решений уравнения (2). Здесь мы их тоже опускаем для простоты.
При полученные выше решения (44)–(48) переходят в уравнения стандартного вида модели NNV, и решения не могут быть построены напрямую другими методами.

4. Заключение

В работе, основанной на связи уравнений с дробной связью и свойствах модифицированной производной Римана-Лиувилля Джумари, мы предложили новый обобщенный метод дробных подуравнений для построения точных решений пространственно-временных уравнений с дробной связью дифференциальные уравнения. Чтобы проиллюстрировать правильность и преимущества алгоритма, мы применяем его к пространственно-временным дробно-связанным уравнениям Конопельченко-Дубровского и уравнениям Нижника-Новикова-Веселова. В результате получается много точных решений. Результаты показывают, что этот новый обобщенный метод дробных подуравнений является прямым, эффективным и может использоваться для многих других дробно-связанных дифференциальных уравнений.

Благодарность

Авторы выражают благодарность рецензентам за полезные советы и комментарии.

Литература

1. И. Подлубный, Уравнения дробных производных , том. 198 of Mathematics in Science and Engineering , Academic Press, Сан-Диего, Калифорния, США, 1999.

   Посмотреть по адресу:

   Zentralblatt MATH | MathSciNet

2. Р. Метцлер и Дж. Клафтер, «Руководство по случайным блужданиям по аномальной диффузии: подход дробной динамики», Отчеты по физике , том. 339, нет. 1, с. 77, 2000.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | MathSciNet

3. К. М. Колванкар и А. Д. Гангал, «Локальное дробное уравнение Фоккера-Планка», Physical Review Letters , vol. 80, нет. 2, стр. 214–217, 1998.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

4. Г. К. Ву, «Метод дробной вариационной итерации для решения дробных нелинейных дифференциальных уравнений», Компьютеры и математика с приложениями , том. 61, нет. 8, стр. 2186–2190, 2011.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

5. HG Sun and W. Chen, «Многомасштабная модель фрактальных производных поперечных ускорений частиц жидкости в полностью развитой турбулентности», Science in China, Series E , vol. 52, нет. 3, стр. 680–683, 2009 г.

   Посмотреть по адресу:

   Сайт издателя | Академия Google

6. В. Чен и Х. Г. Сан, «Многомасштабная статистическая модель полностью развитого ускорения частиц турбулентности», Modern Physics Letters B , vol. 23, нет. 3, стр. 449–452, 2009 г.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

7. Дж. Крессон, «Масштабное исчисление и уравнение Шрёдингера», Journal of Mathematical Physics , vol. 44, нет. 11, стр. 4907–4938, 2003.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

8. Г. Джумари, «Модифицированная производная Римана-Лиувилля и дробный ряд Тейлора недифференцируемых функций, дополнительные результаты», Computers & Mathematics with Applications , vol. 51, нет. 9–10, стр. 1367–1376, 2006.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

9. С. В. Ван и М. Ю. Сюй, «Аксиальное течение Куэтта двух типов фракционных вязкоупругих жидкостей в кольцевом пространстве», Нелинейный анализ. Реальные приложения , том. 10, нет. 2, стр. 1087–1096, 2009.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

10. Цзян X.Y., Сюй М.Ю., «Уравнение теплопроводности относительного времени в общей ортогональной криволинейной системе координат и цилиндрической системе координат», Physica A , vol. 389, нет. 17, стр. 3368–3374, 2010.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

11. Ю. -К. Лю и Дж.-Х. Ма, «Точные решения обобщенного многофракционного уравнения нелинейной диффузии в радикальной симметрии», Сообщения по теоретической физике , вып. 52, нет. 5, стр. 857–861, 2009 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

12. Дж. Х. Ма и Ю. К. Лю, «Точные решения для обобщенного нелинейного дробного уравнения Фоккера-Планка», Нелинейный анализ. Реальные приложения , т. 1, с. 11, нет. 1, стр. 515–521, 2010.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

13. Ю. К. Лю, «Приближенные решения нелинейных уравнений дробного порядка с использованием метода преобразования гомотопических возмущений», Abstract and Applied Analysis , vol. 2012 г., идентификатор статьи 752869, 14 страниц, 2012 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

14. Ю. К. Лю, «Исследование пространственно-временного дробно-нелинейного биологического уравнения в радиальной симметрии», Mathematical Problems in Engineering , vol. 2013 г., номер статьи 654759, 6 страниц, 2013 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

15. Ю. К. Лю, «Вариационный гомотопический метод возмущения для решения дробных начально-краевых задач», Abstract and Applied Analysis , vol. 2012 г., идентификатор статьи 727031, 10 страниц, 2012 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

16. Х. А. Гани и М. С. Мохаммед, «Функциональные решения белого шума для стохастических дробных уравнений КдФ-Бюргерса-Курамото типа Вика», Китайский журнал физики , том. 50, нет. 4, стр. 619–627, 2012.

    Посмотреть по адресу:

    Google Scholar | MathSciNet

17. М. Л. Ван, «Уединенные волновые решения для вариантов уравнений Буссинеска», Physics Letters A , vol. 199, нет. 3–4, стр. 169–172, 1995.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

18. С. Чжан и Х.-К. Чжан, «Метод дробных подуравнений и его приложения к нелинейным дробным уравнениям в частных производных», Письма по физике A , том. 375, нет. 7, стр. 1069–1073, 2011.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

19. Х. Джафари, Х. Таджадоди, Н. Кадхода и Д. Балеану, «Метод дробного подуравнения для уравнений Кана-Хилларда и Клейна-Гордона», Abstract and Applied Analysis , vol. 2012 г., идентификатор статьи 587179, 5 страниц, 2013 г.

    Посмотреть по адресу:

    Сайт издателя | Академия Google

20. B. Tang, Y. He, L. Wei и X. Zhang, «Обобщенный дробный метод подуравнения для дробных дифференциальных уравнений с переменными коэффициентами», Physics Letters A , vol. 376, нет. 38–39, стр. 2588–2590, 2012.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

21. Го С. М., Мей Л. К., Ли Ю. и Сунь Ю. Усовершенствованный метод дробных подуравнений и его приложения к дробным дифференциальным уравнениям пространства-времени в гидромеханике, Письма по физике A , том. 376, нет. 4, стр. 407–411, 2012 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

22. Дж. П. Чжао, Б. Тан, С. Кумар и Ю. Р. Хоу, «Расширенный метод дробного подуравнения для нелинейных дробно-дифференциальных уравнений», Математические проблемы в технике , том. 2012 г., идентификатор статьи 924956, 11 страниц, 2012 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

23. Х. А. Гани, «Точные решения для стохастических обобщенных уравнений КдФ, связанных Хирота-Сацума», Китайский журнал физики , том. 49, нет. 4, pp. 926–940, 2011.

    Посмотреть по адресу:

    Google Scholar

24. А. Х. Гани, А. С. О. Эль Баб, А. М. Забель и А.-А. Хайдер, «Дробно-связанные уравнения Кдв: точные решения и функциональный подход белого шума», , Китайская физика, B , том. 22, нет. 8, артикул ID 080501.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

25. Чжан С., «Метод эксп-функций для уравнения Риккати и новые точные решения с двумя произвольными функциями (2 + 1)-мерных уравнений Конопельченко-Дубровского», Applied Mathematics and Computation , vol. 216, нет. 5, стр. 1546–1552, 2010.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

26. Б.-К. Шин, М.Т. Дарвиши, А. Барати, «Некоторые точные и новые решения уравнения Нижника-Новикова-Веселова с использованием метода Exp-функции», Компьютеры и математика с приложениями , том. 58, нет. 11–12, стр. 2147–2151, 2009.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

Copyright

Copyright © 2013 Yanqin Liu and Limei Yan. Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Идиот Часть I, Главы 1–2 Сводка и анализ

Сводка

Туманным утром в конце ноября поезд из Варшавы прибывает в Санкт-Петербург. Двое мужчин в третьем классе заводят разговор. Один из них — князь Лев Николаевич Мышкин, светловолосый мужчина с седой бородой и голубыми глазами. Другой — Парфен Рогожин, невысокий темноволосый мужчина с маленькими серыми глазами. Вскоре к разговору присоединяется третий мужчина, невысокий, коренастый, с красным носом. Низкопоставленный госслужащий по имени Лебедев, он, кажется, знает все обо всех в Петербурге. Рогожин относится к Лебедеву несколько пренебрежительно.

Князь Мышкин, одежда которого для русского человека кажется несколько странной и все вещи которого умещаются в небольшой узел, возвращается в Россию из Швейцарии после четырехлетнего отсутствия. Покинул Россию из-за болезни, «идиотизма» в сочетании с разновидностью эпилепсии. Господин Николай Андреевич Павлишев поддерживал лечение Мышкина до самой его смерти два года назад. После смерти Павлышева лечащий врач князя, доктор Шнайдер, финансировал пребывание его пациента в клинике в Швейцарии. В Петербурге Мышкин надеется встретиться со своей дальней родственницей госпожой Епанчиной, которой он написал письмо, но не получил ответа. Она жена генерала Епанчина и последняя княгиня в роду Мышкиных, как и Мышкин — последний князь.

Рогожин в большом тулупе на овчине возвращается из российского города Пскова, чтобы потребовать свое наследство в два с половиной миллиона рублей после недавней смерти отца. Рогожин уехал из Петербурга пять недель назад, рассердив отца инцидентом с некой Анастасией Филипповной Барашковой, бывшей любовницей богатого пятидесятипятилетнего дворянина Афанасия Ивановича Тоцкого. Услышав о Настасье Филипповне и увидев ее однажды в балете, Рогожин стал питать к ней глубокую страсть. Когда отец дал ему несколько облигаций в счет погашения некоторых семейных долгов, Рогожин продал облигации и купил Настасье Филипповне бриллиантовые серьги стоимостью десять тысяч рублей. После того, как отец узнал об этом, Рогожин сбежал к тетке в Псков, где внезапно заболел горячкой.

Когда поезд подъезжает к станции, Рогожин приглашает князя и обещает сшить ему новую одежду, после чего они оба могут отправиться к Настасье Филипповне.