Аристотелевская логика: Законы логики Аристотеля, которыми пользуются до сих пор

Содержание

6.3. Аристотелевская логика. Феномен науки [Кибернетический подход к эволюции]

6.3. Аристотелевская логика

Понятия, выражающие свойства ситуации в целом, мы будем называть аристотелевскими, ибо логика Аристотеля есть как раз не что иное, как последовательная теория правильного использования таких понятий. Каждому аристотелевскому понятию соответствует определенное множество ситуаций, а именно тех ситуаций, когда свойство, выражаемое этим понятием, имеет место. Поэтому аристотелевское понятие можно также описать как некое множество или класс ситуаций (явлений, объектов — в том предельно общем смысле, в котором эти термины здесь употребляются, все они равнозначны друг другу и термину «нечто», который из них самый точный, но и самый неудобный из-за необходимости считаться с грамматикой). Поэтому же все законы аристотелевской логики легко выводятся из простейших свойств операций над множествами.

Рассмотрим классический пример силлогизма.

Все люди смертны.

Сократ — человек.

Следовательно, Сократ смертен.

В этом рассуждении участвуют три аристотелевских понятия: «человек», «смертен» и «Сократ». Понятие «человек» характеризуется множеством ситуаций, в которых мы говорим: это — человек. То же относится и к остальным понятиям. Чтобы сделать наглядными свойства множеств, представим каждую ситуацию в виде точки внутри некоторого квадрата (рис. 6.3). Тогда этот квадрат будет олицетворять множество всех мыслимых ситуаций, что соответствует предельно общему понятию «нечто». Остальные понятия, которым соответствуют различные множества точек, будут изображаться различными областями в квадрате. Утверждение «все люди смертны», иначе говоря «каждый человек смертен», означает, что каждая точка, входящая в область «человек», входит также в область «смертен» («смертное существо»), т. е. область «человек» находится целиком в области «смертен». Точно так же вторая посылка силлогизма означает, что область «Сократ» находится целиком внутри области «человек». Отсюда следует, что область «Сократ» находится внутри области «смертен», т.

е. верно утверждение «Сократ смертен».

Нечто

Рис. 6.3. Схема силлогизма о Сократе

Нечто

Рис. 6.4. Схема умозаключения disamis

На рис. 6.4 продемонстрирована справедливость следующей схемы умозаключения (disamis по логической терминологии).

Все A суть B. Некоторые A суть C. Следовательно, некоторые B суть C.

Логика Аристотеля играла важную роль в развитии европейской культуры. Однако она недостаточно глубоко проникает в структуру нашего мышления, она неспособна отразить процесс расчленения ситуации на отдельные части (объекты) и исследования отношений между этими частями. Когда речь идет о свойствах объектов, аристотелевская логика вполне адекватна, ибо можно представить себе изолированный объект как некую ситуацию. Образуя множество таких ситуаций-объектов, мы получаем отвлеченное понятие, выражающее одно из свойств объекта.

Не так обстоит дело с отношениями. Аристотелевская логика может выразить понятие о совокупности объектов, находящихся в данном отношении, но не имеет средств выражения понятия об отношении как таковом. Можно представить множество картинок, имеющих вид контура с пятном внутри; это множество порождает аристотелевское понятие (свойство) «быть контуром с пятном внутри». Но не существует аристотелевского понятия «быть внутри». Логика Аристотеля слишком глобальна, поверхностна. Возьмем такое умозаключение:

Иван — брат Петра. ———————- Следовательно, Петр — брат Ивана.

Умозаключение это правильно, но чтобы его обосновать, надо в явном виде добавить посылку о симметричности отношения «брат», которая здесь неявно подразумевается. Эту посылку можно выразить фразой:

Если х — брат у, то у — брат х.

Здесь буквами x и у обозначаются любые лица мужского пола. Однако такая символика выходит за пределы логики Аристотеля.

Можно ли на языке логики Аристотеля выразить этот силлогизм? Можно, если не рассматривать отдельных людей, а пары людей, точнее, упорядоченные пары, т. е. такие пары, где одному лицу приписывается номер один, а другому — номер два. Вот этот силлогизм совершенно законный с точки зрения аристотелевской логики.

Пара (Иван, Петр) обладает свойством: первый — брат второго. Каждая пара, обладающая свойством: первый — брат второго, обладает свойством: второй — брат первого. ——————— Следовательно, пара (Иван, Петр) обладает свойством: второй — брат первого.

Это громоздкое рассуждение, хотя оно формально и совпадает с предыдущим, бъёт мимо цели, ибо оно не отражает главного в нашем исходном силлогизме — симметричности отношения «брат». Свойства «первый — брат второго» и «второй — брат первого» никак не расчленены, никак не связаны друг с другом и с тем фактом, что они прилагаются к объектам, имеющим вид упорядоченной пары.

Мы не случайно начали кибернетическое исследование понятий с аристотелевских понятий. Они проще, ибо допускают определение исключительно в терминах входных и выходных состояний, без обращения к внутренней структуре распознающей системы. Так было и в истории человеческой мысли. Сначала было осознано наличие аристотелевских понятий и только гораздо позже — отношений.

Так как в математике главное — это исследование отношений между объектами, аристотелевская логика совершенно недостаточна для выражения математических доказательств. Это было замечено давно; примеры из математики, которыми пользуется традиционная логика, говорят сами за себя, они чрезвычайно примитивны и неинтересны. До самого конца XIX в., когда началось создание новой («математической») логики, математика и логика развивались независимо.

Magisteria

MagisteriaÐCreated using FigmaVectorCreated using FigmaПеремоткаCreated using FigmaКнигиCreated using FigmaÐ¡Created using FigmaComponent 3Created using FigmaOkCreated using FigmaOkCreated using FigmaOkЗакрытьCreated using FigmaЗакрытьCreated using FigmaGroupCreated using FigmaVectorCreated using FigmaVectorCreated using Figma�� Created using FigmaEye 2Created using FigmafacebookCreated using FigmaVectorCreated using FigmaRectangleCreated using FigmafacebookCreated using FigmaGroupCreated using FigmaRectangleCreated using FigmaRectangleCreated using FigmaНа полный экранCreated using FigmagoogleCreated using FigmaÐ˜Created using FigmaÐ˜Ð´ÐµÑCreated using FigmaVectorCreated using FigmaÐ¡Ñ‚Ñ€ÐµÐ»ÐºÐ°Created using FigmaGroupCreated using FigmaLoginCreated using Figmalogo_blackCreated using FigmaLogoutCreated using FigmaMail.

ruCreated using FigmaÐœÐ°Ñ€ÐºÐµÑ€ ÑŽÐ½Ð¸Ñ‚Ð°Created using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaРазвернуть лекциюCreated using FigmaГромкость (выкл)Created using FigmaСтрелкаCreated using FigmaodnoklassnikiCreated using FigmaÐCreated using FigmaПаузаCreated using FigmaПаузаCreated using FigmaRectangleCreated using FigmaRectangleCreated using FigmaПлейCreated using FigmaДоп эпизодыCreated using FigmaVectorCreated using FigmaVectorCreated using FigmaСвернуть экранCreated using FigmaComponentCreated using FigmaÐ¡Ñ‚Ñ€ÐµÐ»ÐºÐ°Created using FigmaÐ¨ÑÑ€Ð¸Ð½Ð³Created using FigmaГромкостьCreated using FigmaÐ¡ÐºÐ¾Ñ€Ð¾ÑÑ‚ÑŒ Ð¿Ñ€Ð¾Ð¸Ð³Ñ€Ñ‹Ð²Ð°Ð½Ð¸ÑCreated using FigmatelegramCreated using FigmatwitterCreated using FigmaCreated using FigmaÐ˜Created using FigmavkCreated using FigmavkCreated using FigmaÐ¯Created using FigmaЯндексCreated using FigmayoutubeCreated using FigmaXCreated using Figma

предикатная, формальная и сентенциальная.

Кванторы и возникновение информатики / Хабр

1 | Введение

Логика, как эпистемологический инструмент, — исследующий знание как таковое, — изобретена независимо в трёх отдельных государствах: Греции (Аристотелем), Китае (до правления Цинь Шихуанди) и Индии. В последних двух государствах логика не распространилась настолько, чтобы получить полноценное развитие. В античной же Греции логика сформировалась в своих основах столь определённо, что дополнилась только через 2 тысячелетия…

Значительные изменения в греческую логику, помимо Буля, Моргана и Рассела, внёс Фреге — самая важная фигура основателей формальной семантики. Он разработал логику предикатов и 2 вида кванторов, попытавшись создать «логически совершенный язык» о котором мечтал Лейбниц. Значимой личностью является также Гёдель, который открыл знаменитые две теоремы о неполноте, описывающие невозможность объединения множества доказуемых утверждений со множеством истинных. Он утверждал, что доказательства математики зависят от начальных предположений, а не фундаментальной истины, из которой происходят ответы. Одна из главных идей его работ состоит в том, что ни один набор аксиом, — в том числе математических, — не способен доказать свою непротиворечивость.

На этом этапе некоторые заметят влияние платонизма на австрийского логика. Совершенно верно, ведь Гёдель не раз заявлял о влиянии метафизики Платона на собственную деятельность. Но сам Платон развитию формальной логики способствовал лишь косвенно: в истории он вносит вклад в развитие другого направления — философской логики. Платоном созданы вопросы, на которых основывается вся западная академическая философия вплоть до наших дней. Философия, в том виде, котором она известна, возникла только благодаря учителю Аристотеля.

Платон — учитель Аристотеля

В другие периоды в логику также вносили дополнения:

античной школой стоицизма введены термины «модальности», «материальной импликации», «оценки смысла и истины», которые являются задатками логики высказываний;
также средневековыми схоластами введены несколько понятий;
Готфридом Лейбницем изменена нотация.

Но главное, что сами логические операции не изменились. «Органон» Аристотеля, как сборник из 6 книг — первоисточник, где подробно описаны главные логические законы. «Органон» (с древнегреческого ὄργανον), означает — инструмент. Аристотель считал, что логика является инструментом к познанию. Он объединяет методом получения информации такие науки:

Физика — наука о природе;
Метафизика — наука о природе природы;
Биология — раздел физики, наука о жизни;
Психология — раздел физики, наука о душе;
Кинематика — раздел физики, наука о движении;
И др.

2 | Терминология

У каждой из наук должен быть идентичный фундамент в способе получения гнозисов (знаний), который позволит упорядочить информацию и вывести новые силлогизмы (умозаключения). Только таким образом получится прогресс в познании истины. Без логики наука была бы похожа на коллекционирование фактов, ибо информация бы не поддавалась анализу.

Сам Аристотель находит логике как средству убеждения иное применение: в риторике, спорах, дебатах, выступлениях и т.д., описывая это в труде «Риторика». В западной философии принято давать чёткие определения перед рассуждениями, поэтому определимся с терминами. Логика — наука о правильном мышлении.

В языковой зависимости возникают трудности трактовки термина «наука», но даже в оригинальном названии труда Фридриха Гегеля «Наука логики» — «Wissenschaft der Logik», употребляется слово «наука» (Wissenschaft). Поэтому придём к консенсусу и будем считать, что научной можно назвать ту дисциплину, в которой возможны открытия, исследование и анализ. Логика в таком случае — наука, ибо внутри неё возможно совершать открытия. Яркий пример — комбинаторика Лейбница.

Слово «правильный» веет нормативными коннотациями: правильное поведение, правильное выражение лица, и т.д. Перечисленное соответствует некоторым критериям и логика выставляет их (критерии) для правильного мышления.

Слово «мышление» понимается на интуитивном уровне, но чёткое объяснение затруднительно, обширно и иногда не объективно.

Бюст Аристотеля

3 | Формальная и неформальная логика

Первоначально, деление логики происходит на формальную и неформальную. Формальная логика отличается тем, что, в отличие от неформальной, записывается уравнениями. Неформальная же логика пишется выражениями в форме языка, поэтому она подходит для риторики, а формальная логика для абстрактных наук.

Формальная логика равным образом делится на дедуктивную и индуктивную. Они различаются тем, что в дедуктивном аргументе истинность условий гарантирует истинность умозаключения или вывода. В индукции же, при истинности условий одинаково возможен ложный и истинный вывод.

Законы формальной логики:

1. Закон тождества (А = А): эквивокация или двусмысленность недопустимы. Нельзя подменять одно понятие, другим.

2. Закон непротиворечия (А ∧ ¬А = 0): одно и то же утверждение не может быть истинным и ложным одновременно.

3. Закон исключения третьего или бивалентности (А ∨ ¬А = 1): утверждение может быть либо истинным, либо ложным — третьего не дано.

Принципы формальной логики:

1. Принцип достаточного обоснования: достаточными являются такие фактические и теоретические обоснования, из которых данное суждение следует с логической необходимостью.

4 | Сентенциальная логика (алгебра высказываний)

Базовые операции сентенциальной логики — логики высказываний, где заглавная буква означает предложение:

Отрицание (Утверждение ¬A истинно тогда и только тогда, когда A ложно): если имеем утверждение «А» и имеем утверждение «не А», то, когда утверждение «А» будет истинным — утверждение «не А» будет ложным. Также и когда утверждение «А» будет ложным — утверждение «не А» будет истинным.

Конъюнкция (Утверждение A ∧ B истинно, если и A, и B — истинны. Ложно в противном случае): в английском языке — союз «and/&»; в русском — «и». В утверждении «А и В», между «А» с «В» стоит знак конъюнкции — «∧». Утверждение «А и В» является истинным, если «А» с «В» являются истинными одновременно. Если хоть один элемент ложен, то всё утверждение ложно. «А и В» подразумевает, во-первых: истинность «А», во-вторых: истинность «В».

Дизъюнкция (Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны — утверждение ложно): в английском языке — союз «or»; в русском — «или». Существует два типа дизъюнкции — включающая и исключающая (в логике используется включающее «или»). Условия таковы, что утверждение «А или В» будет истинным, когда один или оба элемента истинны, но никогда — когда оба элемента ложны. Это противоречит нашему обыденному мышлению, т.к. когда спрашивают: «Чай или кофе?» мы выбираем один элемент, но в логике подразумевается выбор не только одного, а нескольких возможных.

Импликация (Утверждение A ⇒ B ложно, только когда A истинно, а B ложно): в английском языке — «therefore»; в русском языке — «следовательно». Подразумевает истинность одного элемента при истинности другого. Потому что условия истинности соблюдаются всегда, кроме случая, когда «А» истинно, а «B» ложно. Поэтому утверждение: «А» ложно, следовательно «B» ложно — истинно. Покажется, что когда «А» ложно, а «В» истинно — не соблюдаются условия, но это не так. Если вы скажете, что после дождя промокните — это утверждение будет истинным вне зависимости от того, пошёл дождь или нет.

Эквивалентность (Утверждение A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны): если истинно утверждение «А, следовательно В» и истинно утверждение «В, следовательно А», то истинными являются выражения «А эквивалентно В» и соответственно «В эквивалентно А». Условия истинности соблюдаются в случаях, когда оба элемента истинны или оба ложны.

Значение переменных		Отрицание (для А)	Конъюнкция («И»)	Дизъюнкция («Или»)	Импликация («Следует»)	Эквивалентность («Равносильно»)
A	B	¬A	A ∧ B	A ∨ B	A ⇒ B	A ⇔ B
0	0	0	0	0	1	1
0	1	0	0	1	1	0
1	0	1	0	1	0	0
1	1	1	1	1	1	1

5 | Предикатная логика первого порядка

В XX веке, после добавлений в область логики работ Лейбница и Фреге, на основе этой дисциплины создаётся новая — информатика. Программирование сохраняет преемственность с видоизменённой логикой Аристотеля — предикатной логикой, описательная способность которой выше, чем у логики высказываний (сентенциальной).

Прежде чем разобрать этот новый тип логики, поговорим об её отличии от сентенциальной. Главная особенность предикатной логики, что заглавными буквами обозначаются предикаты, а не целые высказывания. Можно сказать, что предикат — это математическая функция, которая «накладывает» множество субъектов на множество утверждений.

Высказывание «Я пошёл в зоопарк» — состоит из субъекта и предиката. В нём субъект — «Я», а предикат — то, что остаётся кроме субъекта («пошёл в зоопарк»). Субъект — тот, кто совершает действие в предложении или имеет выраженное свойство; предикат — всё оставшееся. Таким образом, если в сентенциальной логике высказывание «Я пошёл в зоопарк» выражалось бы одной заглавной буквой, то в логике предикатов использовались бы две буквы (заглавная и подстрочная): «P» — для предиката; «x» — для субъекта. Субъекты обозначаются переменной («x»), потому что в предикатной логике появляются две относительно новые операции: универсальный и экзистенциальный кванторы. Особенность кванторов заключается в том, что ими возможно записать выражение истинное при всех возможных переменных «х» или хотя бы при одном.

Универсальный квантор (квантор всеобщности) обозначается символом — «∀», с указанием переменной под ним. Возьмём утверждение «Все пингвины чёрно-белые». В логике высказываний оно бы выражалось как «X ⇒ P», где «X» — нечто являющееся пингвином, а «P» — нечто являющееся чёрно-белым. В предикатной логике же используются субъекты и предикаты, поэтому нечто являющееся пингвином (субъект), обозначалось бы переменной «х» снизу под предикатом. «»х» — является пингвином, следовательно, является чёрно-белым». Записывается так: P(х) ⇒ B(х), где P(х): х — пингвин; B(х): x — чёрно-белый.

Однако этого недостаточно, ведь непонятно, один субъект «х» чёрно-белый или больше одного, а может вообще все. Поэтому утверждение «»х» — является пингвином, следовательно, является чёрно-белым», берётся в скобки и перед скобками используется символ «∀» с переменной «х» под ним — которые вместе и будут универсальным квантором.

Универсальный квантор переводится как: «Для всех «х» истинно, что …». Теперь утверждение «х — является пингвином, следовательно, является чёрно-белым» с универсальным квантором перед ним, расшифровывается так: «Для всех «х» истинно, что «х» — является пингвином, следовательно, является чёрно-белым». Это означает, что чем бы ни был объект во вселенной, если этот объект пингвин — он является чёрно-белым. Полная запись будет выглядеть так:

Экзистенциальный квантор (квантор существования) обозначается символом — «∃» с указанием переменной под ним. Возьмём утверждение «Некоторые пингвины серые». Как и в прошлый раз, выражение «»x» — является пингвином и «х» — является серым» возносим в скобки и ставим перед ними квантор, в этом случае экзистенциальный с указанной переменной. «»x» — является пингвином и «х» — является серым» записывается так: P(х) ∧ C(х), где P(х): х — пингвин; C(х): x — серый.

Экзистенциальный квантор можно перевести так: «Есть такой «х», для которого будет истинно, что …». Подразумевается, что есть как минимум один «х», для которого выполняются условия выражения. Если вам говорят, что ДНК не существует, достаточно показать одну молекулу дезоксирибонуклеиновой кислоты для опровержения этого утверждения. Также и с кванторами, если существует хотя бы один серый пингвин, то утверждение об отсутствии серых пингвинов будет ложно. Полная запись экзистенциального квантора для выражения «Есть такой «х», для которого будет истинно, что «x» — является пингвином и «х» — является серым», будет выглядеть так:

6 | Заключение

Примечательно, что есть возможность перевода одного вида квантора в другой. Возьмём утверждение «Все пингвины не являются серыми». Для универсального квантора текстовая запись будет такая: «Для всех «х», будет истинным утверждение о том, что если «х» — является пингвином, то «х» — не является серым объектом». Но утверждение изменяется и для экзистенциального квантора, используя знак отрицания: «Нет такого «х», для которого бы было истинным утверждение о том, что «x»— является пингвином и «х»— является серым».

В середине XIX века, Готлоб Фреге дополнил логику Аристотеля двумя этими операциями, которые позже сформировались в отдельную дисциплину — предикатную логику. С введением в логику экзистенциального квантора (после универсального) — предикатная логика, в основе своей, завершилась как система…

Источники:

1 — Аристотель: «Органон» — «Первая аналитика» и «Вторая аналитика»;

2 — Аристотель: «Риторика»;

3 — Готлоб Фреге: «Исчисление понятий»;

4 — «Monatshefte für Mathematik und Physik» 1931 г.: Курт Гёдель «О принципиально неразрешимых положениях в системе Principia Mathematica и родственных ей системах»;

5 — The Early Mathematical Manuscripts of Leibniz;

6 — Мельников Сергей: «Введение в философию Аристотеля»;

7 — Гильмутдинова Нина: «Логика и теория аргументации»;

8 — youtube. com;

9 — cyberleninka.ru.

Проблемы бинарной логики, или Почему ИИ — просто усовершенствованный калькулятор

Бинарная логика основана на двух утверждениях: истина (логическая единица) или ложь (логический нуль). Благодаря такому простому механизму возможно быстро и эффективно проводить вычисления. Чтобы машина могла понимать печатные символы и алфавит, используется кодировка ASCII (American Standard Code for Information Interchange). С ее помощью привычный человеку текст переводится в понятные машине нули и единицы.

Однако это не означает, что машина понимает мир и слова так же, как и мы. Нам приходится пользоваться бинарной логикой, чтобы общаться с машиной, но машина не может говорить с нами, пользуясь человеческими мыслительными процессами.

Мы не мыслим нулями, единицами и исключительно количественными категориями. Мы оперируем деталями, контекстами, разными измерениями, динамикой процессов, ценностями и богатством опыта.

Но самое интересное во всём этом, что бинарная логика — это вовсе не изобретение сумасшедших инженеров начала XX века. За бинарную логику стоит говорить спасибо Аристотелю.

Бинарная логика и сексизм Аристотеля

Что? Аристотелю? Отцу демократии и великому философу? За вот эту ущербную машинную логику?

Вообще да, именно ему и его теории дуализма. За 350 лет до нашей эры Аристотелю захотелось сделать мир проще и понятнее. За основу он взял пифагорейскую таблицу противоположностей, которая выглядела примерно так:

Конечность — бесконечность
Чёт — нечет
Единство — множество
Правый — левый
Покой — движение
Прямой — кривой
Добро — зло
и т. д.

Пифагор с помощью этой таблицы демонстрировал, что числа — это не про количество единиц, а про некую силу и вектор ее направления.

Аристотель посмотрел на нее и подумал: ведь разделение на противоположности работает и с людьми, и с животными, и с обществом. Кто-то занимает один полюс, а кто-то — другой. Кто-то прав, а кто-то виноват. Кто-то добр, а кто-то зол.

Аристотель соорудил на фундаменте дуализма иерархическую систему и снабдил ее собственными представлениями о носителях одной полярности (со значением «1») и другой (со значением «0»). Ну, к примеру:

1 = истина = разум = правый = мужчина
0 = ложь = чувства = левый = женщина

Вот такой сексизм 2000-летней давности.

Если бы Аристотель прислушивался к своим предшественникам, Сократу и Платону, он бы, возможно, не был бы так уверен в подчиненном положении женщин и ущербности их разума, и право голоса женщины получили бы не в начале XX века, а гораздо раньше.

В диалоге Платона «Пир» Сократ с большим уважением отзывался о мудрости жрицы Диотимы из Мантинеи, а в Книге 5 «Государства» он говорит, что управлять городом с равным успехом может и мужчина, и женщина.

Тем не менее именно аристотелевская логика легла в основу западной мысли и продолжает пускать ростки стереотипов и предубеждений.

Бинарная логика Декарта и китайская ошибка Лейбница

Эстафетную палочку Аристотеля перехватили в XVII–XVIII веках Декарт и Лейбниц. Декарт, изобретатель афоризма «Я мыслю, следовательно, я существую», зародил идею о том, что любой субъект имеет только ту ценность, которую ему приписывает наблюдатель.

Кроме того, рассуждения Декарта продолжали тенденцию отделения разума от телесных и чувственных проявлений: в «Размышлениях о первой философии» ученый отнес разум к миру идеального, а тела и чувства — к миру материального, где эти два мира не пересекаются.

Плюс Декарт был разочарован несистемными методами, которыми пользовались математики в его время и разработал дедуктивно-индуктивную логику, основы которой изложил в «Рассуждениях о познании». Математика в представлении Декарта должна иметь крепкий фундамент, и в качестве него он использовал аристотелевскую бинарную логику (1 = истина = действительно, 0 = ложь = недействительно), только упаковал ее в древовидную структуру. Теперь она используется в нейросетях при обработке естественных языков.

Немецкий мыслитель и юрист Лейбниц, создатель математического анализа (одновременно с Ньютоном), разработал бинарную модель счисления как быстрый способ получать готовые расчеты.

Интересно, что Лейбниц был ярым китаистом. В 1703 году священник Буве высылает мыслителю копию «Книги перемен» («И Цзин»), древний китайский философский текст. Книга состоит из 64 гексаграмм, в которых Лейбниц уловил сходство с собственными бинарными таблицами и пришел в восторг.

В одних гексаграммах Лейбниц увидел нули, а в других — единицы, что утвердило его в мысли о том, насколько бинарная логическая система универсальна и всеобъемлюща.

Вот только Лейбниц ошибся: во-первых, он рассматривал гексаграммы, перевернув их вверх ногами. Во-вторых, он не учел, что каждая гексаграмма соответствовала определенному описанию на китайском. В третьих, каждая из них представляла собой запись двух противоборствующих энергий — положительной и негативной, инь и ян.

В любом случае и Лейбниц, и Декарт сделали свой вклад в развитие западного мышления, замкнутого в противоестественной дуальной логике.

Бинарная логика сегодня

На бинарной логике построены все современные системы данных. Нулями и единицами пронизаны любые действия, которые производятся сегодня в цифровом поле. Вот, например:

Свайп вправо = 1, свайп влево = 0
Поставили лайк =1, не поставили = 0
Кажется, пользователь испытывает положительные эмоции = 1, отрицательные = 0
Группируем объекты по красному цвету: яблоко = 1, апельсин = 0

Машина лишь регистрирует, какой выбор сделал человек, и дает соответствующую реакцию, выбирая из двух вариантов.

Бинарная логика не предоставляет пространства для моделирования причин принятия подобных решений. Мы собираем черно-белые данные, сортируя их по оттенкам серого, когда мир вокруг — это целая радуга.

Окружающий нас мир не терпит бинарности.

Частицы в квантовой суперпозиции могут быть одновременно и нулем, и единицей. Взаимосвязи между явлениями и свойствами богаче и неоднозначнее, чем чёт и нечет.

Бинарностью легко оперировать, но в таком случае нам стоит смириться с тем, что искусственный интеллект так и останется усовершенствованной моделью калькулятора.

Троичная диалектическая информатика

Н.П. Брусенцов, Ю.В. Владимирова

Неполноценность современной двоичной информатики, наглядно проявляющаяся в невозможности естественного представления чисел со знаком двоичным кодом, обусловлена неадекватностью ее основы — двухзначной логики. Эта так называемая классическая формальная логика, базирующаяся на априорном законе исключенного третьего, не составляет совершенного отображения реальности, не согласуется со здравым смыслом. Потому она, в отличие, например, от арифметики, практически не используется для решения реальных проблем. По существу это логика искусственного дискретного мира двоичных компьютеров. В ней отсутствуют модальности, возможность неотличима от необходимости. Даже фундаментальнейшее логическое отношение содержательного следования вырождено в “материальную импликацию”, парадоксы которой выдающиеся логики упорно, но тщетно пытаются преодолеть на протяжении почти ста лет.

Понятно, почему не удается сделать логику школьным предметом, несмотря на то, что воспитание логичного мышления — первейшая задача школы, как и вузов, в которых логика, хотя и преподается, но не способствует совершенствованию умов. Положение крайне ухудшилось с компьютеризацией образования: ведь при практической безрезультатности разговоров об интеллектуализации машинной обработки информации и об информационной безопасности совершается повсеместное подавление творческого человеческого интеллекта ходульной двухзначной логикой.

Основоположником логики справедливо считается Аристотель, создавший систему доказательного умозаключения — силлогистику, которая все еще остается непревзойденным интеллектуальным инструментом. Силлогистика диалектична, и в ней нет парадоксов, но она не отобразима в современных логических исчислениях, что стало поводом для подозрений, будто у Аристотеля что-то не так, например, будто он не признавал пустых множеств. На самом деле в силлогистике налицо не только пустые, но и нечеткие множества, открытые Л. Заде в 1965 г . и все еще “не освоенные” современной логикой. Но принципиальное отличие логики Аристотеля от современной “классической” в том, что она не двухзначна, а трехзначна [3]. Вопреки “закону исключенного третьего” у Аристотеля наряду с “необходимо есть” и “необходимо нет”, имеется третье — “возможно, есть и, возможно, нет”. Трехзначность присуща отношению следования, исчерпывающе определенному Аристотелем в “Первой аналитике”:

“…Когда два [объекта] относятся друг к другу так, что если есть один, необходимо есть и второй, тогда, если нет второго, не будет и первого, однако если второй есть, то не необходимо, чтобы был первый. Но невозможно, чтобы одно и то же было необходимо и когда другое есть и когда его нет ”.

В силлогистике отношение следования представлено общеутвердительной посылкой Всякое x есть у , сущность которой в том, что всякая x -вещь необходимо есть xy -вещь, а всякая y ? -вещь (не- y -вещь) необходимо есть x?y?-вещь. При этом естественно исключены (невозможны) xy ?-вещи, поскольку x необходимо должно быть у (не может быть у ?). Однако вместе с тем x ? y -вещи не исключены, они возможны , но не необходимы в силу наличия xy — и x ? y ? -вещей. Если же наряду с “Всякое x есть у ” выполняется “Всякое у есть x ”, то будут исключены как xy?-, так и x?y-вещи, т.е. получится отношение эквивалентности — х равнозначно у , выразимое в двухзначной логике: “равнозначно/неравнозначно”. Для отношения же следования требуются три значения: “необходимо есть” / “возможно, но не необходимо” / “невозможно”, поэтому двухзначной импликации для адекватного выражения следования недостаточно. При наличии xy ? -вещей следование невозможно, а если х -вещей нет, то следование не исключено, т.е. возможно, но не необходимо. В случаях же несуществования х -вещей, либо у -вещей, импликация вообще не выражает никакой взаимосвязи между терминами, не составляет двухместного отношения. В этих случаях другой термин волен принимать любое значение независимо.

Для устранения “парадоксов” импликации достаточно предотвратить эти случаи непеременности (константности) ее терминов. Так, строгая импликация Льюиса, представляющая собой несуществование ху? -вещей, т.е. V ?ху? , парадоксально выполняется при несуществовании х -вещей, а также при несуществовании y?-вещей, т.е. при V?х и при V?у?. Парадоксов не станет, если наряду с V ?ху? потребовать V х и V у? — существования х -вещей и у? -вещей. В результате импликация Льюиса превращается в аристотелево необходимое следование VxV?xy?Vу? [1]. В совершенной дизъюнктной нормальной форме этого отношения — VхуV?хVх? — очевидна его трехзначность: наряду с принадлежностью рассматриваемому подмножеству декартова произведения {х, х?} х {у, y ?} членов ху, х?у? и антипринадлежностью ху? умалчивается член х?у . Умалчиванием выражена третья разновидность принадлежности — привходящая, возможная, но не необходимая. Подмножество, допускающее привходящую принадлежность, нечетко, а представленное им отношение трехзначно.

В математической логике отклонение от аристотелева истолкования общеутвердительной посылки “Все А суть В”, превратившее ее из содержательного следования в двухзначную импликацию, Гильберт и Аккерман оправдывали потребностями математических применений логики, “где класть в основу аристотелево понимание было бы нецелесообразно” [2, с. 79]. Они не придавали значения тому, что логика при этом утратила содержательность, полагая, что их логическое исчисление “делает возможным успешный охват проблем, перед которыми принципиально бессильно чисто содержательное логическое мышление” [2, с. 17].

На самом деле бессодержательной логику сделали 2,3 тыс. лет тому назад античные стоики, также стремившиеся к запредельной абстрактности, которая была осуществлена посредством “высказываний”, подчиненных “закону исключенного третьего”, допускавшему для высказывания только два значения “истинности” — “истина / ложь”. Именно двухзначностью адекватная живой реальности силлогистика Аристотеля превращена в мертвую схоластику. Математическая логика лишь выразила эту “классику” в строгих алгебраических формах, с очевидностью выявивших ее неадекватность [3].

Стоики “скомпенсировали” отсутствие в их логике отношения следования с необходимостью осуществлением умозаключений по правилам modus ponens и modus tollens . В математической логике также указывают на то, что импликация — это не следование: “Соотношение”если Х то Y “не следует понимать как выражение для отношения основания и следствия. Напротив, высказывание Х→Y истинно всегда уже в том случае, когда X есть ложное или же Y истинное высказывание [2, с. 20]. Однако вместе с тем в математической логике даже сами ее основоположники отождествляют двухзначную импликацию с трехзначным аристотелевым следованием, поскольку и то и другое ассоциируется с суждением “Все А суть В”. В результате с точки зрения математической логики признаны ошибочными безупречные в действительности модусы силлогистики darapti, damalip, felapton, fesapo [2, с. 79] и отвергается силлогизм подчинения частного общему, ибо согласно отклонению от аристотелева истолкования в суждении “Все А суть В” не содержится с необходимостью “Некоторые А суть В”.

Ян Лукасевич, изобретя в 1920 г . трехзначную модальную логику, в своей обстоятельной книге “Аристотелевская силлогистика с точки зрения современной формальной логики” [4] алгебраически “доказал” путем отождествления трехзначного следования с материальной импликацией, что цитированное выше аристотелево утверждение: “Но невозможно, чтобы одно и то же было необходимо и когда другое есть, и когда его нет” неверно. Оно неверно с точки зрения логики, не соблюдающей основной логический закон — закон тождества. Суждение “Все А суть В”, выражающее отношение следования В из А , нельзя отождествлять с “Ни одно А не есть не-В”, которым в естественном языке представлено двухзначное отношение импликации.

Беда, по-видимому, в том, что логика немыслима без отношения следования, которое в сущности трехзначно и в двухзначной логике естественно отсутствует. Отношение, называемое импликацией, подобно следованию, выражается тем же “если… то” и обозначается той же стрелкой →. Не удивительно, что импликацию принимают за следование. Но если без следования нет логики, то логика с импликацией в качестве следования тем более не логика. В ней из несуществующего следует “все, что угодно”, из “2 в 2 = 4” следует, что “снег бел”.

Это все та же ущербная, пренебрегающая здравым смыслом двухзначная логика, и результат ее внедрения, естественно, не оправдывает ожиданий. Так, в книге Т. Оппенгеймера [5] неопровержимо доказана пагубность компьютеризации обучения в школах США. Автор настаивает на удалении компьютеров из школы, что едва ли осуществимо в сложившейся ситуации. Но ведь корень зла не в компьютерах, а в заложенной в них примитивной, противоестественной логике дискретного двоичного мира, которая прививается учащимся, блокируя их способность овладеть логикой мира реального. Окажись в компьютерах благоразумная естественная логика, результат компьютеризации обучения был бы диаметрально противоположным.

Однако адекватной (диалектической) логики сегодня нет не только в компьютерах, но и во всей “науке о мышлении”, даже в той ее части, которая не подчинена догматическому “закону исключенного третьего” (неправомерно приписываемому Аристотелю) и сосредоточилась на изобретении недвухзначных (“неаристотелевых”) логик. Изобретательство это безуспешно, потому что носит чисто формальный характер. Если бы исследовали проблему по существу, то обнаружили бы, во-первых, что логика Аристотеля трехзначна, а во-вторых, что трехзначность — необходимое, но не достаточное условие адекватности логики. Логика же Аристотеля адекватна, поэтому изобретать неаристотелевы логики нет смысла.

Отрадным исключением является “Символическая логика” Льюиса Кэрролла [6], не нашедшая (как и аристотелева) должного понимания и надлежащего развития. У Кэрролла нет ни бессодержательных “истинных” / “ложных” высказываний, ни “закона исключенного третьего”. Его логика исследует суждения, выражающие взаимосвязи (отношения) вещей, охарактеризованных совокупностями признаков (особенностей). “Во Вселенной множество вещей … Вещи обладают признаками … Любой признак или любую совокупность признаков будем называть также особенностью вещи”.

Суждение рассматривается как естественноязыковое выражение отношения, которым связаны обозначаемые посредством терминов x, y, z, … особенности вещей. Вместе с тем сущность того же отношения Кэрролл наглядно отображает на изобретенной им диаграмме и алгебраически так называемым “методом индексов”, позволяющим формально получить содержательное умозаключение из данных суждений, если оно существует.

Диаграмма Кэрролла внешне тождественна таблице истинности Пирса, используемой для определения булевых функций. Однако истолковывается представленное диаграммой не экстенсионально (не как класс вещей), а интенсионально — как множество вещей, а точнее, как подмножество декартова произведения попарно противоположных особенностей. Кроме того, клеткам диаграммы присваивается не одно из двух, а одно из трех значений — наряду с содержащими “0” либо “1” допускаются незанятые (пустые) клетки, означающие несущественность принадлежности соответствующих им вещей представленному на диаграмме подмножеству. Правда, сам Кэрролл понимал значение “1” как существование, значение “0” как несуществование вещи, а незанятость клетки у него не утверждает ни того, ни другого.

Например, отношение строгой импликации Льюиса V?xy? на двухтерминной диаграмме Кэрролла представлено единственным значением “0” в xy ? -клетке. Кэрролл выражал это отношение трояко: общеотрицательным суждением “Ни один xy? не существует”, либо “Ни один х не есть у? ”, либо “Ни один у? не есть х ”.

Общеутвердительное суждение “Все х суть у ” у Кэрролла содержало в себе необходимо следующее из него частноутвердительное “Некоторые х суть у ”, равносильное суждению существования “Некоторые x у существуют”. Кэрролл называл “Все х суть у” двойным суждением, эквивалентным двум суждениям: “Ни один х не есть у?” и “Некоторые х суть у”, т.е. V?ху?Vху — на диаграмме “0” в клетке xу? и “1” в клетке ху.

Ясно, что это уже не импликация (один из ее парадоксов устранен), но еще и не полноценное аристотелево следование. Не учтена контрапозитивность следования — оплошность, присущая, по-видимому, всем известным попыткам алгебраизации силлогистики. Восполнением этого упущения [7] “Символическая логика” Кэрролла превращается в наредкость стройное и безупречное изложение категорической силлогистики Аристотеля — фундамента диалектической логики.

Важнейшим критерием содержательности логики оказался выявленный в основании силлогистики Аристотеля диалектический принцип сосуществования противоположностей [8]. Контрапозитивность общеутвердительного суждения, как и симметричность отношения, выражаемого общеотрицательным суждением, представляют собой очевидные проявления этого принципа. Сущность же его в том, что обозначаемые посредством терминов x, y, z, … первичные (несоставные) особенности x, x?, y, y?, z, z?, … обретают смысл только в результате сопоставления вещей, обладающих противоположными особенностями, например x-вещи с x?-вещью.

Другими словами, принцип сосуществования противоположностей означает, что подмножеству декартова произведения {х, х?} x {у, у?}, отображающему содержательное отношение, необходимо принадлежат (сосуществуют в нем) все попарно противоположные особенности — V х Vх?VуVу?. На диаграмме Кэрролла выражение VхVх?VуVу? отображается наличием фишки существования “1” на каждой из четырех внутренних стенок, означающим непустоту классов х, х?, у, у?.

Это адекватный реальности Универсум Аристотеля (УА) — основа содержательной логики [8]. Именно в нем льюисова имлликация V?xy? и кэрроллово VхV?xy? необходимо превращаются в полноценное следование:

(V’ху’)(VхVх’VуVу’) ≡ VхуV’ху’Vх’у’;

(VхV’ху’)(VхVх’VуVу’) ≡ VхуV’ху’Vу’.

Несуществование какой-либо из возможных на двухтерминной диаграмме вещей, например ху -вещи, в УА означает существование двух смежных с ней вещей:

(V’ху)(VхVx’VуVу’) ≡ V’хуVхVу ≡ V’хуVху’Vх’у .

Существование же, например, ху’ -вещи в силу принципа сосуществования противоположностей необходимо влечет также существование ее антипода — х’у -вещи. Поэтому частноутвердительная и частноотрицательная посылки силлогистики оказываются двойными и их всего две, а не четыре:

Iху ≡ АхуAух ≡ VхуVх’у’;

Оху ≡ ЕхуЕх’у’ ≡ Vху’Vху’.

Вместе с тем общих посылок оказывается не две, а четыре, впрочем, сводящиеся к одной инвертированием терминов: Еху ≡ Аху’, Ех’у’≡ Aх’у, Aух ≡ A х’у’.

Алгебра силлогистики, соответствующая кэрроллову истолкованию его диаграммы с фишками, символизирующими существование и несуществование вещей, сопоставленных клеткам и разделяющим клетки стенкам, аналогична методу индексов, но вместо индексов использует префиксный функтор существования V — дизъюнкт (интегральная дизъюнкция, подобная интегральной сумме ∑) и его инверсию V’ — символ несуществования. Представленное на диаграмме отношение отображается конъюнкцией дизъюнктов, неинвертированньтх и инвертированных, а члены конъюнкции, соответствующие пустым клеткам, умалчиваются.

Дизъюнктная алгебра компьютеризована путем отображения диаграммы-матрицы в одномерную ДК-шкалу тритов [9], сопоставленных клеткам диаграммы в порядке убывания соответствующих им особенностей: ху, ху’, х’у, х’у’ . Каждый трит принимает одно из трех значений: «+» — существование, «–»- несуществование, «0» — умалчивание. Например, следование (х⇒у)≡ VхуV’ху’Vх отображается значением четырехтритной шкалы: +–0+, частноотрицательная посылка Оху кодируется значением: 0++0.

Всего в силлогистике восемь двухместных отношений [10]:

Аху ≡ Ау’х’ ≡ Еху’ ≡ Еу’х ≡ +–0+

Аух ≡ Ах’у’ ≡ Еух’ ≡ Ех’у ≡ +0–+

Еху ≡ Еух ≡ Аху’ ≡ Аух’ ≡–++0

Ех’у’ ≡ Еу’х’ ≡ Ах’у ≡ Ау’х ≡ 0++–

Iху ≡ I х’у’≡ Iух ≡ Iу’х’ ≡ Оху’ ≡ Оух’ ≡ Ох’у ≡ Оу’х ≡ +00+

Оху ≡ Оу’х’ ≡ Оух ≡ Ох’у’ ≡ Iху’ ≡ Iу’х ≡ Iх’у ≡ Iух’ ≡ 0++0

x ⇔ у ≡ Аху ≡ Аух ≡ Еху’ ≡ Еух’

х ⇔ у’ ≡ Еху ≡ Еух ≡ Аху’≡ Аух’

Компьютеризованное доказательство умозаключений (правильных модусов силлогизма) осуществляется путем представления двухтерминных посылок трехтерминными шкалами, из пересечения которых элиминацией среднего термина выявляется искомое заключение, если оно существует. Например, модус barbara : AуzAху ⇒ Aхz в трехтерминных x , y , z -шкалах реализуется так:

Aуz ≡ + – 0 + + – 0+

Aху ≡ ++– – 00 ++

Aуz ∩ Aху ≡ + – – – 000+

Элиминация y дает x , z -шкалу +–0+, т. е. Axz .

Подчиненность частных посылок общим доказывается пересечением кодирующих эти посылки шкал. Так, подчинение Аху ⇒ Ixy , равносильное АxуIxу = Axу , удостоверяется пересечением +–0+ ∩ +00+ = +–0+

В базируемой на сосуществовании противоположностей силлогистике доказуемы все сомнительные с точки зрения классической логики модусы, а также ряд модусов, упущенных традиционной силлогистикой. Например, из посылок сомнительного модуса bamalip на самом деле следует не только частное, но и общее заключение:

Azy ≡ +0–++0–+

Aух ≡ ++00 – – ++

Azy ∩ Aух ≡ +0 – 0 – – – +

Элиминировав у, имеем +0–+ ≡ Azх ≡ Aх’z’, т. е. AzуAух ⇒ Azх.

Коррекцией традиционной теории является доказательство отрицаемого ею модуса первой фигуры Iyz Аху ⇒ I х z :

Iуz ≡ +00++00+

Aху ≡ ++– – 00++

Iуz ∩ Aху ≡ +0– – 000+,

что по исключении у есть +00+, т. е. I х z

Таким же образом доказуема правильность другого непризнанного модуса первой фигуры IуzЕху ⇒ Охz а также аналогичных модусов других фигур.

Литература

Брусенцов Н.П. Трехзначная интерпретация силлогистики Аристотеля // Историко-математические исследования. Вторая серия. Вып. 8 (43). М.: «Янус-К», 2003.
Гильберт Д., Аккерман В. Основы теоретической логики. М.: ИЛ, 1947.
Лосев Л.Ф. Критические заметки о буржуазной математической логике // Историко-математические исследования.
Лукасевич Я. Аристотелевская силлогистика с точки зрения современной формальной логики. М.: ИЛ, 1959.
Oppenheimer T. The Flickering Mind: The False Promise of Technology in the Classroom and How Learning Can Be Saved. – New York, Random House , 2003.
Кэрролл Л. Символическая логика // Кэрролл Л. История с узелками. М.: Мир, 1973.
Брусенцов Н.П. Диаграммы Льюиса Кэрролла и аристотелева силлогистика // Вычислительная техника и вопросы кибернетики. Вып. 13. М.: Изд-во Моск. ун-та, 1977.
Брусенцов НП. Блуждание в трех соснах: (Приключения диалектики в информатике). М.: SVR — Аргус, 2000. (www.computer-museum.ru)
Брусенцов Н.П., Владимирова Ю.С. Троичная компьютеризация логики // Математические методы распознавания образов: 12-я Всероссийская конференция: сб. докл. М.: МАКС Пресс, 2005.
Брусенцов Н.П. Реанимация аристотелевой силлогистики // Реставрация логики. М.: Фонд Новое тысячелетие, 2005.

Материалы международной конференции SORUCOM 2006 (3—7 июля 2006 года)
Развитие вычислительной техники в России и странах бывшего СССС: история и перспективы
Статья помещена в музей 31.10.2007 с разрешения автора

Лекция 5: Аристотель и его логика

Лекция 5:
Аристотель — Логика

(Продолжение. Начало и полный список лекций вот здесь)

Не менее, если не более, знаменитый, чем его учитель Платон, великий Аристотель появился на свет в Стагрии, Македония в 384 г. д.н.э. В восемнадцать лет он стал студентом платоновской Академии, где обучался и, в последствии, обучал других наравне с самим Платоном вплоть до смерти последнего в 347/8 г.д.н.э

После этого Аристотель, возможно по причине своего макендонского происхождения (понаехали тут…) , не получил позиции главы Академии, и уехал из Афин, занявшись исследованиями в области морской биологии.

В 342 г.д.н.э. Аристотеля призвали ко двору царя Македонии и возложили на него почетную обязанность стать учителем молодого, тогда еще тринадцатилетнего принца Александра. Того самого, впоследствии ставшего Александром Великим.
Закончив обучение семь лет спустя, в 335 году, Аристотель вернулся в Афины, где основал свою собственную школу и исследовательский центр под названием Лицея (да, как и Академия, наименование это вошло в века и используется по сей день).
После смерти Алекстандра в 323 году он вынужден был покинуть Афины. В это время начались гонения на македонян, и он предпринял меры, дабы афиняне «не согрешили против философии второй раз» (первым была казнь Сократа, как вы понимаете). К сожалению, это не сильно помогло – вскоре Аристотель умер, хотя и по естественным причинам.

Уже первоначальное сравнение Аристотеля с Платоном указывает нам на существенную разницу между ними. Так, если Платон был идеалистом, писавшем о потусторонней реальности, то Аристотель выступает как реалист, сторонник научных методов и прагматик.
До некоторой степени это верно, хотя может быть отчасти упрощением и преувеличением. В первую очередь нужно иметь ввиду, что оставшиеся нам от Платона работы представляют собой исключительно его литературные труды, рассчитанные на широкого читателя. Есть сведения, что он так же давал лекции, и имел работы более технического характера, до нас недошедшие. В то же время от Аристотеля нам остались только его рабочие записи, конспекты лекций. Опять же есть основания полагать, что у Аристотеля имелись и литературные труды, которые были впоследствии утрачены.
Так или иначе, разница между учителем и учеником есть, и очень существенная, и мы еще о ней поговорим. Для начала дадим общий обзор его подхода к теории познания.

Опыт

Аристотель начинает свою «Метафизику» знаменитой фразой:
«Все люди от природы стремятся к знанию.» (980а)

Но как получить знание? В отличие от Платона, Аристотель уверен, что знание можно получить только посредством опыта.
Для Аристотеля, знание начинается с изучения конкретных, а не общих вещей. Только начав с конкретного можно перейти к более фундаментальным, общим истинам. Врач, говорит Аристотель, не пытается излечить «идею человека», он пытается излечить конкретных людей – Сократа или Каллия. Таким образом, практическое знание начинается с индуктивных обобщений, сделанных на основании опыта.

Дерево.

Предположим, перед нами дерево. Насколько различен подход к его изучению мог бы быть у артиста, садовника и ученого?

Артист: пришел бы в восторг от индивидуальности и особенности данного дерева (нет должного обобщения)
Садовник: задумался бы, какие удобрения для него использовать? (его знание – функционально, и пытается ответить на вопрос «как?» а не «почему?»)
Ученый: ищет понимания деревьев посредством их универсальных характеристик:

— пытается извлечь суть дерева и отделить ее от случайных его черт
— пытается понять причины каждого отдельного факта и какое место они занимают в общей схеме необходимых связей.

ОРГАНОН

Язык, мысль, реальность

Одним из фундаментальных принципов у Аристотеля является единство структуры языка, мысли и реальности. С его точки зрения, когда мы рассуждаем от одного утверждения к другому, мы не просто совершаем мысленный процесс. На самом деле мы переходим от одного фрагмента информации об окружающем нас мире к другим фактам, составляющим его реальность.
Возникающая в результате цель состоит в том, чтобы поняв базовую структуру языка и мысли понять через них и базовую структуру реальности как таковой, ибо язык является сочленением реальности, ее наиболее фундаментальным фактором.
Именно этой цели служит набор книг о логике, традиционно именуемый «Органоном» (др.-греч. Ὄργανον — инструмент, метод ). В средние века именно Органон был основным набором сочинений Аристотеля, над которым трудились схоласты, устанавливая отношения между субстанциями и универсалиями.

Десять основных категорий.

Категории (др. -греч. Κατηγορίαι, лат. Categoriae или Praedicamenta) — первое по порядку сочинение в «Органоне» Аристотеля, в котором перечисляются все возможные виды того, что может быть субъектом или предикатом суждения.

Десять категорий определяются Аристотелем исходя из вопросов, ответ на который дает каждая категория. Так,

1. Субстанция, или «сущность» (др.-греч. οὐσία, отвечает на вопрос «Что это?») Примеры: «этот единичный человек» или «это единичное дерево».

2. Количество (др.-греч. τὸ πόσον — отвечает на вопрос «сколько?») Количество дает, таким образом, пространственно-числовые характеристики вещи. Примеры – «два метра длинной», «два килограмма весом».

3. Качество (др.-греч. τὸ πόιον отвечает на вопрос «какое?») Качество, таким образом, это предикат, который характеризует все неколичественные свойства предмета. Примером качества может служить «мудрый», «железный», «красный», «твердый».

4. Отношение (др.-греч. τὸ πρὸς τί — «то, по отношению к чему», отвечает на вопрос «как это соотносится?») Отношение, таким образом, это тот способ, которым одна вещь может быть связана с другой. Примеры: «половина», «больше», «меньше».

5. Пространство (отвечает на вопрос «где это?») определяет положение вещи относительно ближайшего окружения. Примеры: «на площади», «в саду»

6. Время (отвечает на вопрос «когда?») определяет положение вещи относительно последовательности событий. Примеры: «вчера», «сегодня».

7. Состояние (ситуация, отвечает на вопрос «в каком положении?») определяет положение друг относительно друга. Примеры: «лежит», «сидит».

8. Обладание (отвечает на вопрос «в каком состоянии?») указывает на наличие внешнего обстоятельства вещи. Примеры: «одетый», «цветущий».

9. Действие (др.-греч. τὸ ποιει̃ν — «действовать», отвечает на вопрос «что это делает?») Примеры «говорит», «смеется».

10. Претерпевание (отвечает на вопрос «что на это действует?»), передает принятие изменения от некоторого другого предмета. Примеры: «обжигается», «арестовывается».

Субстанция

Субстанция для Аристотеля – особая категория. Субстанция лежит «в основе всего», и все остальное является ее предикатом либо находится «в ней». Субстанции могут быть субъектом утверждений, к которым относятся остальные девять категорий. В то же время они единственные имеют независимое существование в реальности, в то время как остальные категории существуют только лишь постольку, поскольку «находятся» в субстанциях.

Среди субстанций Аристотель отличает «первые сущности», индивидуальные субстанции, от «вторых сущностей», которые являются универсалиями. Согласно этому, «Сократ» — первая сущность, в то время как «человек» — вторая сущность.

Логика

Аристотель по праву считается первым, кто обнаружил и описал основные правила рассуждения, которые мы называем «логикой». Смысл тут в том, что для того, чтобы рассуждение было действенным, оно должно следовать определенной процедуре, гарантирующей, что из истинных утверждений в аргументе всегда будет следовать истинное заключение.

Логика Аристотеля касалась тех возможных вариантов, посредством которых мы можем рассуждать о взаимодействиях между категориями.
В целом, мы можем сделать четыре варианта утверждений касательно отношений меж двумя категориями. Допустим, мы относим категории «студентов» и «поэтов», тогда следующие варианты соотношения становятся возможны:

1. Все студенты это поэты
2. Ни один студент не является поэтом
3. Некоторые студенты это поэты
4. Некоторые студенты это не поэты

Из таких предпосылок складывается аргумент.

Аргумент

Аргумент это такая конструкция, в которой одна группа утверждений, посылки, дает основания для другого утверждения, заключения. Одна из наиболее распространенных форм аргумента это силлогизм.

Силлогизм

Силлогизм (др.-греч. συλ-λογισμός — «подытоживание, подсчёт, умозаключение», от др.-греч. συλ- (συν-) — приставка со значением совместности действия, соучастия и др.-греч. λογισμός — «счёт, подсчёт; рассуждение, размышление») это такое рассуждение мысли, которое состоит из трех утверждений: двух посылок и одного заключения.

Пример силлогизма:

Все матери это женщины (большая посылка)
Некоторые родители это не женщины (меньшая посылка)
————
Следовательно, некоторые родители это не матери (заключение)

Валидность

Валидность рассуждения не зависит от содержания аргумента, и определяется его структурой.
Аргумент вверху имеет следующую структуру:

Все П это М
Некоторые С это не М
Следовательно, некоторые С это не П

Где С – субъект, П – предикат и М – средний термин.
Валидной считается та форма, в которой любые последовательно вставленные на место соответствующих обозначений (С, П и М в данном случае) термины сохраняют истинность посылок и следующего из них заключения (истинно-предохраняющая форма).
Некоторые формы исходно невалидны.

Первые принципы

Аристотель понимал, что не все утверждения могут быть дедуктивно продемонстрированы. Как основание для аргументов необходимы некие аксиомы, или посылки, истинные сами по себе, и не зависящие ни от чего другого. Такие аксиомы он именовал «первыми принципами».
Первые принципы могут быть установлены через процесс индукции и интуиции.

Индукция

Универсальные и необходимые свойства неустойчивого мира единичных вещей могут быть познаны посредством индукции (обобщения).
Это происходит, в частности, когда многочисленные ощущения одного и того же типа подтверждают друг друга и накапливаются в памяти, и из них начинает возникать знание сходных универсальных качеств реальности. По сравнению, сделанному самим Аристотелем, это как солдаты, удержавшие позиции и продвинувшиеся все дальше на территорию противника. Так же и универсалы продвигаю наше познание все дальше и дальше в сторону обобщенного знания.

Интуиция

Основные предпосылки для обоснования через интуицию следующие:
— Мир устроен рационально
— Эта рациональность не может быть познана только на основании опыта, но опыт может подсказать нам ее очертания
— Только посредством интеллектуальной интуиции мы в состоянии познать универсальные и неизменные истины, лежащие в основе всего подлинного знания

Интуиция, таким образом, является следующим шагом после процесса индукции. В определенном смысле она похожа на «воспоминание» Платона, однако у Аристотеля это скорее «узнавание», чем «воспоминание».

Два основных класса Первых Принципов

1. Уникальные, фундаментальные принципы и определения, присущие каждой отдельной области науки

2. Законы логики:

а) Закон не-противоречия: «А не может быть одновременно Б и не-Б»
б) Закон исключенной середины: «А должно быть или Б или не Б»
в) Закон идентичности «А это А»

О метафизике Аристотеля — в следующий раз

4. ЛОГИКА | Симпосий Συμπόσιον

Аристотелевская логика излагается в собрании текстов, получившем название Органон (что означает «орудие» или «инструмент» науки). Представленная в более или менее аксиоматической форме, логика позволяет с помощью особых правил и процедур вывести знания, уже некоторым образом имеющиеся в наличии или же подлинно новые (об этом часто идут споры) из непосредственно истинных положений, которые есть в каждой науке.
Первые два сочинения, входящие в Органон, — Категории и Об истолковании — трактуют одно о понятиях, другое — о высказываниях. В 1-й главе Категорий Аристотель различает одноименные предметы (у которых общее имя, а соответствующие этому имени определения разные) и соименные (когда определение у двух различных слов одно и то же: человек и бык называются «живыми существами»). Одноименность очень важна для аристотелевской онтологии, поскольку благодаря отношению одноименности о сущем говорится в различных смыслах.
Одна из основных задач Аристотелевой логики — устранение двусмысленностей в рассуждениях. В Софистических опровержениях, последнем сочинении из Органона, скрупулезно перечисляются разные виды погрешностей и двусмысленностей, допускаемых в доказательствах, будь то намеренно или неосознанно. А в книге Δ Метафизики помещен целый философский словарь, который дает ясное представление о многозначности каждого термина.
Желание Аристотеля устранить двусмысленность связано с его стремлением постичь всю действительность в категориях, или общих понятиях. Мы видели, что перечень категорий включает субстанцию, количество, качество, отношение, место, время, положение, состояние, действие и претерпевание (Категории, 4; несколько отличный перечень категорий мы находим в Топике I, 9: примечательно, что первая названная здесь категория — ti esti / τί εστί, «суть бытия» или «определение», а не oysia/ούσία, «субстанция»). Аристотель делает упор на то, что «каждое из перечисленного [т. е. каждая из категорий] само по себе не содержит никакого утверждения; утверждение или отрицание получается сочетанием их» (Категории, 4, 2 а 4-8).
Греческое слово katēgoria/κατηγορία, традиционно передаваемое как «категория», может быть переведено и термином «предикат», более ясно выражающим функцию категорий. Поскольку всякое высказывание имеет вид «Р принадлежит S»[1] (или же: «Р есть свойство S»), предикат Ρ соединяется с субъектом S посредством связки «быть (свойством)»[2] соответственно различным формам, которые Аристотель называет также «схемами предикации» (skhēmata tes katēgorias), или, иначе, соответственно различным схемам соединения предиката с субъектом. Грамматическая структура играет здесь существенную роль: она раскрывает, что в совокупности высказываний типа «Р принадлежит S» и «S принадлежит Q», следовательно, «Р принадлежит Q» есть один термин (в данном случае S), который может выполнять функцию среднего термина — среднего в буквальном смысле, так как он находится между меньшим и большим терминами. Классификация категорий у Аристотеля, как мы видели, непосредственно связана с обыденной языковой практикой. Категории — это и неразложимые семантические единицы, и выражение различных смыслов «сущего», которые соотносятся с его основным смыслом, состоящим в обозначении субстанции. Хотя Аристотель и не доказывает, что приведенный им перечень категорий является полным, он, очевидно, полагает, что всякая атрибуция предикатов укладывается в одну из десяти установленных схем предикации. Аристотель подчеркивает, что у категорий нет общего элемента. Он не допускает, например, возможность квантификации качества (характеризующей современную физику) , но зато допускает, что можно мыслить субстанцию предмета независимо от мест, последовательно занимаемых им в пространстве, от проявляемых им качеств, от его количественных изменений и т. д.
Главный вопрос, который ставит перед нами понятие категории вместе с перечнем категорий, равнозначным для Аристотеля перечню предикатов, — дает ли этот перечень логическую или же онтологическую классификацию. Когда Аристотель заявляет, что из «сказанного (ta legomena) без какой-либо связи» каждое означает или субстанцию, или другие категории (1 b 25), он, видимо, подразумевает, что категории охватывают всю реальность и что, следовательно, предложенная классификация носит онтологический характер. Однако различия, существующие в реальности, постижимы только через языковые разграничения (еще раз напомним, что katēgoria означает также «предикат», хотя термин «предикат» не подходит в том случае, когда речь идет о первых субстанциях: они логически не предикаты, а субъекты, о которых сказываются другие вещи). Категории, представляющие, по Аристотелю, предельно широкие классы, на которые делится вся реальность, служат и военной машиной против платонизма. В своей критике положения Платона о том, что умопостигаемые идеи онтологически предшествуют реальным единичным вещам, Аристотель прямо не прибегает к определению категорий; однако он особо подчеркивает, что все либо сказывается о единичных субстанциях, либо находится в этих субстанциях (2 b15-37).
Основной объект логических исследований Аристотеля — высказывания (apophansis/άπόφανσις, logos apophantikos / λόγος άποφαντικός)[3]. В 4-й главе трактата Об истолковании он проводит различие между «речами» (logoi), означающими всякое словосочетание, обладающее смыслом, и «высказываниями» (apophanseis/άποφάνσεις), которые утверждают или отрицают нечто о предмете. «Всякая речь (logos), — пишет Аристотель, — что-то обозначает, но не как естественное орудие, а, как было оказано, в силу соглашения. Но не всякая речь есть высказывающая речь, а лишь та, в которой содержатся истинность или ложность чего-либо» (4, 17 а 1-4). Предмет аристотелевской логики, таким образом, составляют преимущественно высказывания, которые могут быть истинными и ложными (повеления же, просьбы, вопросы и т. п. оставлены для риторики: 17 а 4-6). Речь может быть истинной или ложной постольку, поскольку она утверждает либо отрицает одно относительно другого. Высказывания, или речи, бывающие истинными или ложными, всегда сводятся к приписыванию некоторого предиката некоторому субъекту посредством связки «есть». «Сократ говорит» преобразуется в «Сократ есть говорящий». Речи, составляющие предмет логики, могут быть простыми либо сложными. Но Аристотель, видимо, колеблется, называть ли речью в строгом смысле слова, logos, сложные формулировки, образованные, например, соединением простых речей; ведь не всегда на вопрос об истинности формулировок такого рода можно ответить «да» или «нет». Логику сложных «речей», или логику высказываний, позднее разработают стоики.
Два других важнейших сочинения, излагающих аристотелевскую логику, — Первая Аналитика и Вторая Аналитика. Их главная цель — установить правила вывода. Хотя этот раздел Аристотелевой логики, вопреки притязаниям автора Аналитик, не исчерпывает логику во всей ее полноте, он представляет собой величайшее философское достижение. Теория силлогизма преподавалась до конца XVIII в.; Кант и Гегель еще указывали на нее как на самую совершенную по форме логическую дисциплину. Она замечательно построена и обнаруживает решительное притязание на всеобщность.
Аристотель отмечает, в Первой Аналитике, что существует четыре типа высказываний, в которых один термин (предикат) утверждается или отрицается относительно другого термина (субъекта): общеутвердительные высказывания (утверждающие Ρ относительно всякого S; такие высказывания стали обозначать буквой А), общеотрицательные высказывания (отрицающие Ρ относительно всякого S; обозначаются буквой Е), частноутвердительные (утверждающие Ρ относительно некоторого S; обозначаются буквой I) и частноотрицательные (отрицающие Ρ относительно некоторого S; их обозначают буквой О). Общее высказывание — это такое высказывание, в котором предикат принадлежит либо не принадлежит субъекту во всем его объеме, а частное высказывание — высказывание, в котором предикат принадлежит либо не принадлежит части объема субъекта. Например, высказывание: «Быть живыми существами присуще (hyparkhei/ύπάρχει) всем людям» (или: «Живые существа — это признак всех людей», или же: «Все люди — живые существа»), в котором «быть живым существом» присуще всякому человеку или сказывается (katēgoreitai/κατηγορείται) о всяком человеке, — это общее высказывание. Общее (katholoy/καθόλου) высказывание не всегда истинно («Все люди бессмертны» — пример ложного общего высказывания). Оно истинно в частном случае, когда предикат принадлежит всем индивидуумам, подпадающим под понятие данного субъекта, субъекта per se[4], в отношении которого это высказывание должно быть сущностно, а не акцидентально истинным. Возможно также, что некоторый атрибут приписывается всем индивидуумам, подпадающим под понятие данного субъекта, и этот субъект представляет самый широкий класс, какому данный атрибут может быть приписан. В этом случае атрибут является общим. «Под общим я разумею то, что присуще всем <предметам, принадлежащим к данному роду,> само по себе и поскольку оно есть то, что оно есть. Очевидно поэтому, что все, что есть общее, присуще вещам необходимо. «Само по себе» и «поскольку оно есть то, что оно есть» означают одно и то же, как, например, точка и прямая сами по себе присущи линии, ибо они присущи, поскольку линия есть линия. Точно так же треугольнику, поскольку он треугольник, присущи <в совокупности> два прямых угла, ибо и сам по себе треугольник равен двум прямым {углам}. Общее же присуще тогда, когда оно может быть доказано относительно любого <из предметов данного рода> и относительно первого <из них>; например, иметь <в совокупности> два прямых угла присуще не всякой фигуре; хотя относительно некоторой фигуры и можно доказать, что она имеет <в совокупности два прямых угла, однако не относительно любой фигуры […] Любой же равнобедренный треугольник имеет углы, равные <в совокупности> двум прямым, однако не как первое, так как первее это имеет треугольник <вообще>. Стало быть, тому, относительно чего как любого первого можно доказать, что оно имеет <в совокупности> два прямых угла или что-либо другое, — этому первому присуще общее, и доказательство этого само по себе есть <доказательство> общего; доказательство же другого есть доказательство как-то по-иному, не само по себе, и доказательство общего дается не относительно равнобедренного треугольника, а простирается на большее» (Вторая Аналитика I, 4, 7з b 26-74 а 3)[5].
Существуют также неопределенные высказывания, в которых не уточняется, принадлежит ли предикат субъекту во всем его объеме или же он принадлежит только части объема субъекта. Кроме того, высказывания могут представлять различные модальности: «Всякая… посылка есть посылка или о том, что присуще, или о том, что необходимо присуще, или о том, что возможно присуще» (Первая Аналитика I, 2, 25 а 1-2). Высказывания различных модальностей, определенных Аристотелем, впоследствии получили название ассерторических, аподиктических и проблематических.
Итак, высказывания бывают простыми либо состоящими из простых (не будем забывать сделанную выше оговорку об оценке истинности сложных высказываний), утвердительными либо отрицательными, общими либо частными, ассерторическими, аподиктическими либо проблематическими. Эти подразделения, возможно, покажутся современному читателю самоочевидными, но Аристотель первым осмыслил и ясно сформулировал их. Например, в 10-й главе трактата Об истолковании (19 b 10 сл. ) он пунктуально разбирает, как могут попарно комбинироваться утверждения и отрицания, и показывает, в частности, что противоречащим высказыванию «Всякий человек справедлив» будет не «Всякий человек несправедлив», а «Неверно, что всякий человек справедлив».
Первая Аналитика внешне очень похожа на современные труды по логике, потому что Аристотель заменяет предложения схемами предложений. Конкретные термины замещены у него буквами (А, Б, В). Формула силлогизма по первой фигуре выглядит так: «если А сказывается обо всех Б, а Б — обо всех В, то А необходимо сказывается обо всех В» (Первая Аналитика I, 4, 25 b 37-39). Огромное преимущество подобной формулировки — в ее обобщенности: если общая схема правильна, она окажется верифицированной для любого частного значения букв. Использование букв вместо терминов позволяет выявить соотношения между схемами высказываний, представляющими известные общие характеристики; если бы высказывания были сформулированы с помощью частных терминов, их правильность казалась бы проблематичной.
Другой существенный элемент логического учения, изложенного в Первой Аналитике, — распознание, каким образом простые высказывания могут составлять совокупность посылок, позволяющую выводить заключения. Это то, что Аристотель называет syllogismos/συλλογίσμός; («силлогизм»): «силлогизм… есть речь, в которой если нечто предположено, то с необходимостью вытекает нечто отличное от положенного, в силу того что положенное есть» (Первая Аналитика I, 1, 24 b 18-20). Истинное заключение может быть выведено не из всякого сочетания посылок; с другой стороны, некоторые сочетания посылок не позволяют вывести никакого заключения. Поэтому Аристотель объединяет группы посылок в фигуры и для каждой из фигур указывает, в соответствии с характерными для нее модусами, какой тип заключения может быть в данном случае выведен. Это систематичное представление групп посылок с целью выведения заключения и есть силлогистика в строгом смысле слова. Силлогистику можно рассматривать и как развитие теории вывода, и как первый опыт создания особой науки — формальной логики. Аристотель стремился вместить все дедуктивные выводы в определенные схемы доказательств, группируя посылки, из которых выводятся заключения. Но, вопреки уверенному заявлению Аристотеля, что «всякое доказательство и всякий силлогизм необходимо получаются посредством трех ранее указанных фигур» (I, 23, 41 b 1-3), многие дедуктивные выводы, формальная структура которых не укладывается в схемы Аристотелевой теории простого высказывания, остаются за рамками этой теории.
Силлогизм в его наиболее распространенной форме состоит из двух посылок и заключения. Иногда Аристотель представляет его как вывод: «А присуще всякому Б; Б присуще всякому В; следовательно, А присуще всякому В». Но чаще всего силлогизм выражается в виде условного предложения: «Если А присуще всякому Б и если Б присуще всякому В, то А присуще всякому В». В одном пассаже из Первой Аналитики четко излагается общая формула такого силлогизма по первой фигуре, в котором есть только общие высказывания, утвердительные либо отрицательные: «. ..Если три термина так относятся между собой, что последний {т. е. меньший[6]} термин целиком содержится в среднем, а средний целиком содержится в первом {т. е. в большем} или вовсе не содержится в нем, то для этих крайних терминов необходимо имеется совершенный силлогизм. Средним термином я называю тот, который сам содержится в одном, в то время как в нем самом содержится другой, и который по положению оказывается средним. Крайними же я называю и тот, который содержится в другом, и тот, в котором содержится другой. […] Если же первый термин сопутствует всему среднему, а средний не присущ ни одному последнему, то крайние термины не составят заключения, ибо при таком <отношении термииов> ничего с необходимостью не вытекает… А если из этих терминов ничего с необходимостью не вытекает, то нет и силлогизма» (I, 4, 25 b 32-26 а 8). Например: А присуще всем Б, Б присуще всем В, следовательно, А присуще всем В; Б служит здесь средним термином. Но не все силлогизмы правильны: сочетание трех высказываний «А говорится обо всех Б», «А говорится обо всех В», следовательно, «Б говорится обо всех В» не образует правильного силлогизма. Из 256 возможных форм силлогизма правильны только 24.
Силлогистика Аристотеля — большое достижение в истории логики. Аристотель был не первым философом, попытавшимся представить правильные доказательства в формальном виде. Формализацией умозаключений до него интересовался Платон (см., например, Федон, 92 c-d и Теэтет, 162 е). Но Аристотель предложил первое систематичное описание форм дедуктивных выводов; он ввел символы, распространяющиеся на любой термин, он изучил условия правильности доказательств и сформулировал правила следования. Однако силлогистика Аристотеля имеет дело лишь с такими высказываниями, которые выражают отношения включения либо исключения классов. Она, собственно, не затрагивает других отношений между классами. Кроме того, символы, применяемые Аристотелем, относятся к терминам, но не к высказываниям. Логика высказываний будет разработана через несколько десятилетий стоиками.
Первой Аналитике, в которой содержится довольно стройная концепция силлогизма, можно противопоставить трактат Об истолковании, где рассматриваются проблемы, касающиеся статуса высказываний. Верно ли, что все высказывания состоят из простых высказываний? Верно ли, что все высказывания включают только два термина? Как быть с отдельной категорией имен — именами собственными, ни частными, ни общими? Наконец, в какой мере установленное Аристотелем деление высказываний на частные и общие учитывает эпистемологический статус положений естественных наук, констатирующих, что по природе такое-то животное «чаще всего» бывает таким-то или таким-то? Подобные высказывания можно выразить общей формулой «В большинстве случаев S есть Р», поскольку всегда сохраняется возможность, что некоторое животное не будет таким-то или таким-то. Как бы то ни было, одна из трудностей аристотелевской логики заключается в том, что выражение «чаще всего», обозначающее у Аристотеля модальность, в которой описываются природные явления, нельзя понять, если придерживаться строгого разделения общего и частного.
Наконец, надо сказать несколько слов об исследовании правил диалектической дискуссии, составляющей предмет одного из самых ранних философских произведений Аристотеля — Топики, последняя книга которой была издана отдельно под заглавием О софистических опровержениях. Этот тип спора, когда обе позиции определены и один из собеседников старается защитить свой тезис от аргументов противника, требует применения диалектического силлогизма. Диалектический силлогизм основывается на посылках, выражающих не истины, а всего лишь правдоподобные (endoxa) мнения, или же мнения, имеющие определенную значимость, так как их придерживаются мудрые люди — «все, или большинство из них, или самые известные и славные».
Заключим этот беглый обзор аристотелевской логики словами из последней главы Софистических опровержений, в которой Аристотель изъясняет замысел и цель своего сочинения: «Итак, о том, на скольких основаниях получаются паралогизмы в рассуждениях… для чего полезны все такого рода доводы, как вообще следует отвечать и как надо раскрывать доводы и погрешности в речи, — обо всем этом было сказано нами» (34, 183 а 26-34). «Что касается настоящего учения, то дело обстояло не так, что частью оно было заранее разработано, а частью нет: в наличии не было ровно ничего. […] Если же вам, рассматривающим это учение, созданное вначале при таких обстоятельствах, оно кажется вполне удовлетворительным по сравнению с другими учениями, расширявшимися на основе предания, то остается сказать, что вам, слушателям, следует быть снисходительными к упущениям в этом учении, а за все изобретенное нами — глубоко признательными» (183 b 3336,184 b 2-8).

[1] В русских переводах логических сочинений Аристотеля принадлежность предиката субъекту принято передавать словом «присуще» («А присуще (hyparkhei) Б»). Однако такой перевод едва ли удачен, когда логическим предикатом является случайное свойство или состояние. Одно из значений глагола hyparkhein — «иметься, быть в наличии». Поэтому универсальный вариант, подходящий для всех типов предикатов, — «Р есть (имеется) у S», или «Р принадлежит S». Французский переводчик во всех аналогичных случаях пользуется словом appartenir («принадлежать»).
[2] Более привычная для нашего читателя формулировка при помощи глагола-связки — «S есть Р».

[3] Греческому apophansis (и его латинскому эквиваленту propositio) в русской логической литературе соответствуют термины «суждение» и «высказывание». В настоящее время преобладает второй вариант.
[4] Самого по себе (лат.).
[5] Перевод Б. А. Фохта («ФН») с изменением в первой фразе: вместо «…и само по себе, и поскольку…» — само по себе и поскольку…
[6] Рассматриваемый здесь модус силлогизма по первой фигуре (AAA) в традиционной логике обычно обозначается так:
Все M суть Р.
Все S суть М.
Все S суть Р.

В символах Аристотеля —

Все Б суть А.
Все В суть Б.
Все В суть А.

У Аристотеля, поскольку он пользуется другой формой обозначения, меньший термин В (субъект заключения) — последний, а больший А (предикат заключения) — первый:

А присуще всем Б.
Б присуще всем В.
А присуще всем В.

Аристотелевская логика: логика категорий

[Обратите внимание: описание, которое я здесь даю, не отражает исторические мотивы Аристотеля и его интерпретацию логической системы, которую он разработал, которая очень сильно связана с его более широким философским мировоззрением. То, что я здесь описываю, скорее, является стандартной интерпретацией аристотелевской логики в том виде, в каком она представлена в современных текстах по символической логике.]

Аристотелевская логика — это логика классов или категорий, поэтому ее часто называют «категориальной логикой».

Или, скорее, это логика утверждений, которая может быть представлена в терминах классов вещей, и отношений между этими классами .

Например, утверждение на естественном языке «Все коровы — млекопитающие» будет представлено как отношение между классом коров и классом млекопитающих (а именно, что класс коров является подмножеством из класс млекопитающих или, что то же самое, что все члены класса коров также являются членами класса млекопитающих).

Аристотелевская логика дает нам инструменты для представления утверждений следующей формы, которые называются «категориальными утверждениями»:

Все S являются P
Некоторые S P
№ S а р
Некоторые S не-P

Они отражают структуру субъект-предикат широкого класса утверждений, но, конечно, не всех утверждений.

Категориальный силлогизм — это аргумент, состоящий ровно из трех категориальных утверждений (двух посылок и заключения), в которых фигурируют в общей сложности ровно три категориальных термина, каждый из которых используется ровно дважды.

Примеры:

1. Все люди — млекопитающие.
2. Некоторые строители — люди.
Следовательно, некоторые млекопитающие — строители.

1. Гуси не относятся к кошачьим.
2. Некоторые птицы гуси.
Следовательно, некоторые птицы не относятся к кошачьим.

Аристотель исследовал все логически различные типы силлогизмов, которые можно было создать с помощью основных категориальных утверждений, и определил, какие дедуктивно действительные, а какие нет.(В системе Аристотеля существует четырнадцать действительных форм. Средневековые логики дали им всем имена.)

Итак, какой фрагмент естественного языка, логическая структура которого способна моделировать аристотелевская логика?

Это фрагмент естественного языка, который включает утверждения с двухместной структурой субъект-предикат, где субъект и предикатные термины могут быть представлены как классы объектов, а логические отношения между утверждениями определяются отношениями включения. , исключение и перекрытие между классами.

Вот и все.

Одно из самых увлекательных занятий на уроках символьной логики — это научиться переводить выражения естественного языка в логический синтаксис конкретной логической системы. Неформально мы называем этот перевод с английского (say) на «logicese» (по аналогии с «китайским», «японским» и т. Д.).

Для лингвистов, специализирующихся в области лингвистики, основное преимущество работы с подобными упражнениями заключается в том, что они помогают осознать грамматические и логические особенности языка, на которые в противном случае вы бы не обратили внимания.

Например, «Некоторые подростки — сотрудники McDonald’s» легко перевести , потому что и подлежащее, и предикатные термины — это существительные во множественном числе — каждое обозначает класс объектов. Вот для чего была создана категориальная логика.

Существительные множественного числа могут функционировать как подлежащие или предикатные термины в категориальном высказывании. «Некоторые сотрудники McDonald’s — подростки » так же грамматически правильно сформированы, как « Некоторые подростки — сотрудники McDonald’s» .

Но теперь рассмотрим это утверждение: «Некоторые подростки дезорганизованы» .

Если вы поменяете подлежащее и сказуемое термины, то получите следующее: « Некоторые неорганизованные — подростки» . Это уже не грамматически правильно построенное предложение.

Проблема в том, что слово «неорганизованный» — это прилагательное , а не существительное. Прилагательные используются для модификации существительных, обычно они не могут существовать отдельно.

Чтобы записать это в «logicese» аристотелевской логики, вам нужно переписать прилагательное как существительное во множественном числе, например:

«Некоторые неорганизованные люди — подростки.”

Теперь подлежащий термин обозначает класс людей, а не просто прилагательное.

Еще примеры переводов упражнений с английского на логический синтаксис аристотелевской логики:

«Нарушители будут привлечены к ответственности».
- = «Все нарушители — это люди, которым грозит судебное преследование».
«Требуется некоторая сборка».
- = «Некоторые части этого предмета требуют сборки.”
«Нет боли — нет выгоды».
- = «Никакие упражнения без физической боли не являются упражнениями, дающими физическую выгоду».

Весело, правда? Конечно, они могут быть неудобными и роботизированными, но эти переводы действительно предлагают определенную ясность в отношении того, что на самом деле утверждается.

Аристотелевская логика была разработана таким образом, чтобы мы могли переводить многие виды утверждений естественного языка в утверждения об отношениях между классами. Полный блок по этой теме покажет вам, как переводить такие утверждения:

«Сократ — человек».
- (предметный термин относится к физическому лицу)
«Где дым, там и огонь».
- (в подлежащем термине используется наречие)
«В местном аквариуме водятся акулы».
- (предметный термин имеет подразумеваемый количественный показатель — некоторые акул, не все акулы)
«Не всякий роман о романтике интересен.”
«На арену могут выходить только люди с билетами».
«Пицца — это здоровое блюдо, если в ней есть овощная начинка».
- (Условные отношения)

Аристотелевская логика мощна и оставалась доминирующей системой логики, преподаваемой в университетах в течение 2400 лет. Но как теория дедуктивного мышления она имеет важные ограничения. Аристотель считает некоторые формы аргументов действительными, чего мы не сделали бы сегодня, и не включает формы аргументов, которые мы могли бы признать действительными.

Один из парадоксов интеллектуальной истории состоит в том, что, хотя евклидова геометрия является величайшим достижением греческой дедуктивной науки, а теория силлогизма Аристотеля была задумана как теория дедуктивного доказательства , , теория силлогизма не может объяснить даже простейшего доказательства в евклидовой геометрии.

Для этого есть несколько причин, но основная причина в том, что не все предложения геометрии имеют простую форму субъект-предикат.На самом деле их довольно мало. Вместо этого геометрические доказательства имеют дело с отношениями между объектами, а система Аристотеля не предназначена для моделирования отношений. Кроме того, не все утверждения геометрии имеют только один квантор; по существу они могут включать повторных использований слов «все» и «существует».

Есть и другие причины, но в результате даже простые математические выражения и математические доказательства не могут быть представлены в аристотелевской логике, и это связано с выразительными ограничениями системы — она моделирует только фрагмент естественного язык и рассуждения на естественном языке.

Природа логики Аристотеля

Аристотель, как естествоиспытатель и философ, пытался классифицировать почти все, от животных до понятий. Более того, он классифицировал различные аспекты того, что может быть известно о любой вещи. Он перечислил 10 типов информации, которые могут относиться к предмету, и назвал их « категорий ». Категории — это классы информации, которые могут относиться к любой «вещи». Он перечислил их как « вещество , количество , качество , отношение , место, время, положение, состояние, действие или привязанность».Субстанцию можно понять как реальную существующую вещь, которую можно познать с помощью наших органов чувств. Остальные категории он назвал «случайностями», которые могут описать существенное. Можно сказать, что человек субстантивен. Этот человек может иметь вес в 140 фунтов, качество интеллекта, отношение быть вдвое ниже другого человека, место нахождения на рынке и время вчерашнего дня. Эти классы информации передаются через предложения, у которых есть субъект и предикат, где субъект — это то, к чему относится информация, а предикат включает в себя информацию.

Что удалось сделать Аристотелю, так это представить целую систему логики, которая систематизирует информацию о любых вещах и обо всех вещах. Это очень сложный и разносторонний аргумент, состоящий из сети предложений, каждый вывод которых можно проследить до его предпосылок. Логика изложена через предложений , определяемых как «утверждение или утверждение, выражающее суждение или мнение». Предложения содержат субъект и предикат .Отношения субъект-объект также являются основой грамматики, формы, с помощью которой язык (по крайней мере, западный язык) организует значение. Мы можем организовать все, что мы знаем о мире, используя всего четыре формы предложения, как изложено ниже: весь день светлый, никакая ночь не светлая, некоторые дни теплые, некоторые дни нет. Мы можем описать любую вещь, которую мы видим, с точки зрения того, что она собой представляет и от чего отличается. Субъект — это агент, о котором у нас есть мнение, а в грамматике сказуемое — это предложение, содержащее глагол и говорящее о субъекте.

Аристотель строит свою систему логики из предложений, которые подтверждаются истинностью более ранних предложений, на которых они основаны, и соблюдением законов и правил логики. Эта система логики создает серию последовательных, внутренне связанных, аргументов . Если мы начнем с двух предпосылок, основанных на наблюдении за материальной реальностью, мы можем прийти к заключению, которое также будет соответствовать материальной реальности. Каждый вывод из серии аргументов можно использовать в качестве гипотезы, которую затем можно проверить на предмет реальности, часто с помощью эмпирической науки. Здесь есть значительный риск: если какая-либо посылка ложна, огромная и сложная система логического мышления, в свою очередь, может оказаться полностью ложной. Если вы полностью полагаетесь на логику, вы должны быть уверены в своих предпосылках.

Аристотель начинает свою систему логики с утверждения: «все s есть p». Это абстрактное утверждение , на данном этапе оно не описывает конкретную реальность . Слово «абстрактный» здесь действительно важно. Я собираюсь много использовать абстракцию и абстракцию в представлении диалектики.Здесь я определяю абстрактное как «существующее в мысли или в качестве идеи, но не имеющее физического или конкретного существования». Это слово происходит от латинского abstractus , «вытянутый». Здесь содержание было удалено от символов s и p. «Абстрактный» часто используется как уничижительный термин, например, «это просто абстрактный аргумент». Однако абстрагирование невероятно полезно. Математика и есть такая форма абстракции. Мы знаем, что 1 плюс 1 равно 2. Здесь 1 является абстрактным и может представлять собой что угодно.Но из этого утверждения мы знаем, что если у нас есть одна корова, и у нас есть другая корова, у нас есть две коровы. Очевидно, что это более полезно, когда используемые термины более сложные. Противоположностью абстрактному является конкретное, часто определяемое как «реальное», «материальное», «существующее». Сегодня довольно сложно не думать о строительном материале. Бетон происходит от латинского concrescere , или «расти вместе».

A, E, I, O

Утверждение «all s is p» настолько абстрактно и настолько просто, что кажется бесполезным.Но это предпосылка, на которой основана эта логическая система. Это первичное предложение входит в набор из четырех, представленных Аристотелем, каждое из которых известно буквой:

A Все s is p

E Номер p

I Some s is p

O Некоторые s не p

Здесь «s» и «p» оба являются терминами предложения. Буква «s» представляет тему , которая, в свою очередь, представляет все предметы, которые могут быть использованы в этом предложении. Он абстрактен в том смысле, что отделен от любых реальных примеров.Буква p в нашем предложении представляет собой предикат . «S» — это , связанное с «p», и предложение устанавливает характер отношения. Мы также можем сказать, что «s» — это , определяемое как «p»: в нашем утверждении s стоит само по себе, а p полезно, потому что оно что-то говорит нам о s. Что действительно важно здесь — фактически, все, что мы можем узнать из этого утверждения, — это соотношение между «s» и «p». Одна из самых важных вещей в диалектике заключается в том, что отношения имеют наибольшее значение, даже больше, чем природа s или p.Диалектика — альтернатива философии Рене Декарта (1596-1650), который, говоря простыми словами, предположил, что существует разделение разума (человеческого сознания) и материи (всего остального) и что материя является механической. Если бы вы использовали декартовский научный метод, вы бы разбили s на части и выяснили, из чего они сделаны. Предполагается, что это поможет нам раскрыть истинную природу «s». В диалектике s определяется своим отношением к p. Теперь мы хотим определить это отношение

В нашем основном утверждении «all s is p», «all» называется квалификатором , а «is» — связкой.Аристотеля интересует соотношение между этими высказываниями. Используемые здесь квалификаторы «все» и «нет» описываются как универсальный ; «некоторые», а также «некоторые … не» как , в частности . Философия глубоко озабочена универсальностью. Если мы знаем, что факт верен в отношении всех вещей, это намного полезнее, чем знать, что верно только в отношении некоторых вещей. Это меня интересует, потому что проблемы, с которыми мы сталкиваемся, и решения, которые нам нужны, влияют на всех нас и потребуют от всех нас, чтобы добиться успеха.Разница между всеми и некоторыми уже давно является фундаментальной для политики: универсальная декларация прав человека логически должна применяться ко всем людям (а не, например, только к мужчинам или белым людям). Разница между универсальным и частным описывается как разница в количестве . Все что-то за вычетом некоторого количества чего-то становится каким-то: и в этом случае какое-то есть, а какое-то нет.

Разница между квалификаторами «all» и «some … is» в отличие от квалификаторов «no» и «some»… не ». Первый (все) называется утвердительно , а второй (нет) отрицательно . Разница между положительным и отрицательным описывается как разница качества . Определение и использование отрицания, а также отношения между качеством и количеством — это навязчивая идея диалектики. Здесь мы можем сделать вывод, что при изменении количества между универсальным (всем) и частным (некоторыми) происходит также качественное изменение между положительным и отрицательным.Давайте начнем с «все s есть p», где величина «all» применима к s. Мы знаем, что s имеет свойство утвердительно относиться к p во всех случаях. Когда мы меняем предложение с «все s есть p» на «некоторое s есть p», мы должны сделать вывод, что «некоторое s не является p», по крайней мере, возможно. Здесь качество s в первом предложении остается положительным, но из этого следует, что «some s не p» возможно — и, следовательно, s также может иметь качество отрицательного в некоторых случаях. Это означает, что когда мы меняем количество s со всех на некоторые, качество также меняется с положительного на, возможно, и утвердительное, и отрицательное по отношению к p.

Все это начинает казаться полезным здесь и сейчас, когда мы можем вывести одно утверждение из одного или двух других в процессе, известном как вычет . Это один из методов расширения наших знаний за пределы того, что мы можем наблюдать, за пределы наших ощущений. Аристотель использовал следующий пример. Возможно, мы знаем, что «у всех собак четыре ноги». Затем нам говорят, что «Фидо — собака». Тогда мы можем сделать вывод, что у Фидо четыре ноги, без необходимости наблюдать за Фидо. Это очень полезная гипотеза, но ее нужно проверить на практике.Мы смогли узнать новую информацию, например, «Фидо перенес операцию по удалению ноги». Однако статистически вполне вероятно, что у Фидо четыре ноги — полезная информация, если мы покупаем ему в подарок собачьи тапочки.

Утверждение, с которого мы начинаем, известно как предпосылка , а то, с которым мы делаем вывод, называется выводом . Акт перехода от начала к заключению — это , вывести . Если мы начнем с одной посылки, мы получим сразу .Если мы начнем с двух или более предпосылок, вывод будет опосредован : первая посылка опосредована вторым, чтобы сделать вывод. (Обратите внимание, что здесь «немедленно» не будет означать «без долгого прохождения времени», а вместо этого «с одной предпосылкой, а не с двумя». Это хороший пример того, где определения, используемые в логике, похожи, но не такие, как обычно использовал). Вот что произошло с Фидо: предпосылка о том, что Фидо — собака, опосредована предпосылкой о том, что у всех собак четыре ноги, чтобы сделать вывод о том, что у Фидо четыре ноги.

Как мы видим, при представлении аргумента или предложения первое, что нужно сделать, — это проверить, согласны ли вы с предпосылками. Если вы не согласны с тем, что у всех собак по четыре ноги — некоторые попали в аварию — тогда вам также следует оспорить этот вывод. Мы можем видеть, почему универсальные утверждения более полезны, чем конкретные утверждения: если вы замените все некоторыми в предпосылке Фидо, вы получите «у некоторых собак четыре ноги» и сможете только сделать вывод, что у Фидо может быть четыре ноги, а может и нет.Логика более полезна, когда мы можем вывести серию предложений из предпосылки или предпосылок, создавая совокупность знаний из того, что может быть единичным фактом. Длинная цепочка предложений, каждое из которых основано на первом, известна как сориты — сориты с двумя предпосылками известны как силлогизм .

Атомы

Демократ (c460 до н.э. — c370 до н.э.), древнегреческий философ и современник Аристотеля, заметил, что каменные статуи выдерживают атмосферные воздействия. Он отметил a. твердые, физические объекты изнашиваются и теряют свои края и b.вещество, которое необходимо удалить, было невидимо невооруженным глазом. Исходя из этих двух посылок, он пришел к выводу, что даже большие объекты из твердого материала на самом деле состоят из частей, которые были настолько малы, что их нельзя было обнаружить человеческим зрением. Он отметил, что на самом деле все объекты материальной реальности со временем трансформируются. Из этого он пришел к выводу, что все материальные объекты были сделаны из объектов, слишком маленьких, чтобы их можно было увидеть. Он описал их как «атомы» или неделимое. Спекулятивная философия, логическая дедукция привели к знанию, которое на тысячи лет опередило естественные науки.

Аристотель пошел на все, чтобы выяснить, что произойдет, если вы измените каждую из различных частей предложения, и что произойдет, если вы сложите одно предложение поверх другого. Он начал с того, что утверждал, что «s» и «p» одинаковы во всех предложениях, как ученый, выделяющий переменные в эксперименте. Он продолжает, глядя на то, что произошло бы, если бы вы просто поменяли местами подлежащее и сказуемое; и что произойдет, если вы измените квалификаторы, заменив «все» на «некоторые» (и наоборот).Сейчас это может показаться до боли скучным, но позже станет увлекательным и полезным — и мы знаем, что должны привести наши предпосылки в порядок, если хотим вывести что-нибудь полезное.

Начнем с немедленного вывода, потому что это проще. Когда мы начинаем менять местами части предпосылки, это называется воспитанием (а различные способы называются простым преобразованием; преобразование путем ограничения и возражения). Аристотель установил, что в предложении «все s есть p» нельзя предполагать, что можно поменять местами s и p.Все s равно p не эквивалентно всем p is s (если s равно p). Как мы можем просто показать, когда мы меняем местами s и p вот так, иногда то, что мы создаем, является допустимым, а иногда — недействительным. Например, мы знаем, что «все люди — животные» — это правда, но мы также знаем, что «все животные — люди» — ложь. Аристотель изучил постулаты и разработал каждый случай, когда можно было поменять местами вещи и при этом иметь предположения, которые были логически верными. Вот почему полезна логика — мы можем проверить, является ли вывод, который мы сделали из одной истины, чтобы установить более позднюю, предполагаемую истину, действительным или недействительным.В некоторой степени это может помочь нам узнать, кому верить, а кому не верить, без необходимости выходить из химической лаборатории во время ночного разговора в пабе о том, «вся ли философия бесполезна» или просто «какая-то философия бесполезна».

Аристотеля особенно интересовало, как каждая форма предложения A, E, I и O соотносится с другими формами, когда s одинаково во всех предложениях и p также одинаково. Мы знаем, что каждая из четырех форм предложений различна либо по качеству, либо по количеству.Он установил, что с некоторыми предложениями вы можете поменять местами подлежащее и сказуемое, и ваше заключение останется верным, но некоторые окажутся ложными. Но мы также можем видеть, что некоторые формы противостоят другим — если одна из них истинна, другая ложна. Совершенно очевидно, что «все есть р» противоречит утверждению, что «нет есть р». Они не могут быть правдой одновременно. Однако «some s is p» согласуется с «some s is not p». Как мы вскоре увидим, концепция оппозиции, пожалуй, самая важная в диалектике.

Природа противоположностей между предложениями завораживает. Существует четыре типа противодействия: , противоречие, , противодействие, субсогласование и субатернизация. Нам больше всего пригодится «противоречие». Предложение находится в противоречии со вторым утверждением, когда истинность первого сразу же подразумевает ложность второго, и, более того, когда истинность второго немедленно предполагает ложность первого. Из этого мы можем видеть, что A противоречит O: если «все s есть p», то мы знаем, что «some s не p» не может быть истинным, но ложным.Мы также знаем, что если «some s is not p» истинно, то «all s is p» ложно. Это определение противоречия в диалектической логике. В общем языке противоречие часто можно использовать для всех противопоставлений. Однако определение обратного несколько иное. Здесь мы можем сделать вывод из истинности первой посылки, что вторая посылка ложна; но мы можем только заключить из ложности первой посылки, что вторая посылка истинна или ложна. Итак, если мы знаем, что «all s is p» истинно, мы можем сделать вывод, что «no s is p» ложно.Но если мы знаем, что «all s is p» ложно, мы можем знать только то, что «some s is p» может быть либо истинным, либо ложным. Таким образом, противоречие более радикальное и к тому же симметричное.

Со времен Аристотеля произошло два особенно полезных развития традиционной логики для нашего анализа: акцент на отрицании в девятнадцатом веке, а также современный акцент на предложениях, где термины «s» и «p» представляют собой « категорий ». , который я объясню более полно при следующем обсуждении Гегеля. Логика Аристотеля выдерживала серьезную проверку за столетия с тех пор, как он впервые ее выдвинул. Более поздние разработки, включая концепцию отрицания и концепцию o, расширили и продвинули их.

Отрицательный

Введение отрицательных значений для s и p расширяет и улучшает исходную логику Аристотеля. Профессор Джеймс Викенсон Миллер утверждал в статье Структура аристотелевской логики в 1938 году, что «отрицательные термины имеют большое преимущество перед традиционной логикой.С одной стороны, они увеличивают мощность и масштаб системы. С другой стороны, они приводят к подлинному упрощению системы ». (стр. 93). Второе утверждение Аристотеля (E), «нет s есть p», включает отрицательный определитель «нет», как отмечалось выше. Однако Гегель и другие расширили его, чтобы включить отрицательные значения для самих терминов: «не-s» и «не-р». Теперь у нас может быть пропозиция «все не-р» и пропозиции с двойным отрицанием, такие как «нет s не-р». Это можно охарактеризовать как отрицание отрицания, опять же, термин, существенный для диалектики Гегеля.Это подводит нас к особенно важному моменту. Утверждение «all s is s» теперь не то же самое, что «s is s» и не эквивалентно ему, поскольку «all s» включает термин с отрицательным значением «non-s». Утверждение «s не-s» является противоречием, оно по определению ложно. «Закон тождества», лежащий в основе диалектики, описывает «s is s», но не может быть расширен до «all s is s». Мы вернемся к этому позже.

Вторым недавним дополнением к традиционной логике является введение концепции «класса».Класс, или классификация, подобен корзине объектов, в которой эти объекты, собранные в корзину, имеют одну или несколько характеристик. Следовательно, «красный» — это класс объектов, которые человеческий глаз видит в красном цвете. Красный класс существует независимо от того, есть ли объекты красного цвета и все объекты в классе красные. Слова могут функционировать в языке как категории. Слово «люди» относится к тем вещам, которые можно классифицировать как «человеческие». У них есть все свойства, которые идентифицируют их как людей.Предложения, которые мы представили до сих пор, содержат переменные «s» и «p». Эти термины являются пропозициональными функциями. Когда мы заменяем эти переменные члены фиксированным значением, мы получаем предложение. Например, «x есть человек» — это пропозициональная функция. Когда переменная x заменяется значением «Энни», мы получаем «Энни — человек», что является истинным утверждением. Когда мы заменяем переменную x на Fido, мы получаем утверждение, что Фидо — человек, которое неверно. Говорят, что те значения, которые заменяют переменную для создания истинного предложения, удовлетворяют пропозициональной функции.

Класс «человек» — это те сущности, которые удовлетворяют пропозициональной функции «x есть человек». (p85) Наиболее общее определение класса содержится в описаниях: «класс, не имеющий членов» и «класс, членство в котором совпадает со всей вселенной дискурса». (p85) Класс без членов называется нулевым классом, а последний — классом юниверса. Профессор Миллер представил доказательство, демонстрирующее, что включение современного определения и использования класса в традиционную логику является последовательным.Далее он утверждал: «Традиционная логика и современная логика полностью согласуются друг с другом. Очевидные разногласия между ними отражают просто разницу в словарном запасе … Современная логика, конечно, гораздо более обширная система, чем традиционная логика. [Традиционная логика] действительно является частью логики, но только ее частью. Это особый случай ».

Преимущество представленной здесь логики — формы чистого разума — состоит в том, что как идеализированная систематизация понятий она не зависит от нашей интерпретации мира вокруг нас.Наука продвинулась вперед за последние две тысячи лет, но аристотелевская логика осталась такой же надежной и полезной, как и тогда, когда она была впервые развита. Однако использование логики сильно ограничено, когда она не связана с материальной реальностью или не основана на ней.

Реальность

Так чем же сегодня нам полезна логика? Я хочу представить аргумент о природе изменений в личном, групповом и социальном масштабе. Этот аргумент относится к нашей материальной реальности: каков мир на самом деле и каковы на самом деле люди, населяющие этот мир.Первая предпосылка этого аргумента проста: Вселенная состоит из дифференцированной материи. Это утверждение основано на наблюдении, а не на предыдущем предположении. В нашем мире есть, например, вещи, которые мы можем ощутить зрением, звуком, осязанием, запахом и вкусом, а есть вещи, которые мы не можем. Для Демокрита, древнегреческого философа, который ввел понятие атома, есть материя и пустота. Это отличается от Гегеля, идеалиста, чья логическая система не опирается на ссылку на материальную реальность.Первые посылки — это концепции чистого бытия и ничто. Отношения между этими концепциями и природой, которую мы ощущаем, очень сложны, и мы вернемся к этому позже.

Вторая предпосылка этой серии состоит в том, что человеческий разум — это дифференцирующая машина. Это тоже основано на наблюдении. Через зрение я могу различать световые волны разной длины, создавая ощущение цветов. Мозг — это дифференцирующая машина, но в равной степени это машина, которая выявляет сходства.Он может идентифицировать два яблока как одинаковые, а апельсин как разные. Это дуэльное движение катагоризации. Это материалистическая (где мы начинаем с существующей реальности, а не логических концепций), а не идеалистическая основа для большей части того, что следует в нашем определении и обсуждении идентичности и различия. Есть разница между материальной вселенной и человеческим разумом. Однако есть и тождество: материальный мир можно дифференцировать, а человеческий разум может его различать.Здесь нас интересует идентичность — общие свойства, пересекающаяся реальность — между миром и разумом. Проще говоря, это то, что Гегель описал как Geist , что переводится как «дух» и «разум».

Цель этой книги — понять изменения в личном, командном и общественном масштабе. Каждый из них явно существует на пересечении человеческого разума и материальной вселенной. Следовательно, природа ума (без материальной реальности) и материальной реальности (без разума) — это философская область, которая выходит за рамки.Спор о том, существует ли диалектика в естественном мире или является просто продуктом человеческого разума, здесь не рассматривается. Но я утверждаю, что мы получим огромную пользу от интерпретации и организации информации с помощью диалектики, поскольку мы пытаемся понять все, что может быть известно человеческому разуму обо всей естественной вселенной.

Этот краткий обзор аристотелевской логики необходим, но недостаточен для моего представления диалектики. Он вводит определения таких слов, как подлежащее и сказуемое, тождество, отрицание, отрицание отрицания, непосредственное и опосредованное, противопоставление и противоречие, среди других.Эти определения окажутся неоценимыми, когда мы исследуем гегелевское изложение диалектики. На собственном опыте я изучал значение диалектики в обратном направлении: начиная с грубой и неточной версии, которую я узнал от некоторых академических марксистов, затем из моего собственного (неправильного) понимания произведений Маркса, затем от Гегеля и, наконец, до Аристотеля. Если эта серия больше ничего не добьется, я надеюсь, что она поможет хотя бы некоторым людям избежать этой ошибки.

Начав с Аристотеля и его определения этих терминов, мы можем продвинуться к пониманию диалектики, которая является последовательной, последовательной и невероятно мощной в нашей интерпретации мира вокруг нас.Хотя, учитывая сложность концепции, это понимание никогда не будет полным, тотальным или фиксированным. Отношения между подлежащим и сказуемым будут основой нашего понимания отношения между человеком и природой. Нас будут особенно интересовать отношения, которые находятся в оппозиции. К термину «противоречие» мы еще вернемся при объяснении диалектики, а также организационной науки и теории систем. В следующем тексте я надеюсь изложить некоторые универсальные утверждения о нас, людях.Я буду утверждать, что некоторые формы поведения можно найти у всех людей, всех человеческих групп и всех взаимодействий между людьми и природой.

Автор

Брендан Монтегю — редактор журнала Эколог.

Арка аристотелевской логики

Доктрина предшествующих моделей

и Posterior Analytics

Аристотель (384-322 до н.э.) родился Ἀριστοτέλης (лат. Aristoteles) в греческой колонии Стагира на полуострове Халкидики, недалеко от того места, где позднее располагались монастыри на горе.Афон. Это было также недалеко от столицы Македонии Пеллы, куда отец Аристотеля пришел работать придворным врачом. В 17 лет Аристотель отправился в Афины, чтобы учиться в Академии Платона, где он был настолько выдающимся учеником, что люди стали называть его «Разумом», νοῦς, Академии.

Однако, когда Платон умер в 347 году, Аристотель не стал его преемником. Это могло быть связано с некоторым кумовством, поскольку племянник Платона был следующим схолархом, Σχολάρχης, «правителем школы».«Аристотель решил искать счастья в другом месте. После некоторых приключений, опасностей и трагедий это в конечном итоге привело его обратно в Пеллу, где он получил работу наставником сына короля, мальчика, который станет будущим Александром Великим. У нас есть понятия не имел, чему его учил Аристотель, или какими будут их отношения, или какими они будут в будущем. Вместо этого, хотя Александр взял с собой племянника Аристотеля Каллисфена во время вторжения в Персию, Александр в конечном итоге казнил его ( 327), очевидно, из-за разногласий.

Между тем Аристотель вернулся в Афины в 335/34 г. и основал свою школу, лицей Λύκειον, который также находился в роще, как и Академия, за пределами Афин, но на противоположной стороне города от Академии. Сократ упоминает, что видел там Евтифрона, что означает, что там, возможно, была спортивная площадка, спортзал , γυμνάσιον («место, где можно раздеться») и, возможно, там была ванна. Именно здесь Аристотель развил свою зрелую мысль, хотя ничего из этого нам не оставили, кроме конспектов лекций, которые нужно было систематизировать, отредактировать и опубликовать после его смерти — с такими аномалиями, как случайное название книги «Метафизика ».

Из всех областей философии Аристотеля логика по-прежнему затрагивает актуальные вопросы. Действительно, современные и недавние философы часто пренебрегали самыми основными вопросами логики. Это одна из причин важности фризской школы, которую Карл Поппер справедливо хвалит за успехи в этих вопросах.

Удивительно, как часто мы обнаруживаем, что вещи игнорируются или неправильно понимаются, что было ясно и решительно описано Аристотелем.Таким образом, и Лейбниц, и логические позитивисты считали, что логика может быть сведена к математической и механической системе, так что все проблемы философии могут быть решены просто «расчетом» без беспорядочного посредничества мысли. Слава Богу! Нам больше не нужно думать ! Что это будет означать, стало очевидным, когда позитивисты унаследовали и развили формы современной символической логики, которая выглядела так, как будто она должна соответствовать условиям того, что первоначально предполагал Лейбниц.

Однако Лейбниц, логические позитивисты и все их дисциплины полностью игнорировали и игнорировали то, что, возможно, является наиболее фундаментальной чертой дедуктивной логической аргументации. Таким образом, само определение действительного дедуктивного аргумента, которое применимо как к символической логике, так и к логике Аристотеля, состоит в том, что аргумент действителен тогда и только тогда, когда невозможно, чтобы посылки были истинными, а заключение — ложным. Таким образом, , если посылки верны, заключение должно быть истинным.Это большое «если». Дедуктивный аргумент и вся символическая логика хороши ровно настолько, насколько хороши его предпосылки. Но что делает посылки верными? Да, вот в чем загвоздка.

Это означает, что принцип компьютерного программирования «Мусор на входе — мусор на выходе» также применим ко всей логике. И это также означает, как сказал Роберт Хайнлайн, что если вы дадите философу достаточно статьи, он сможет доказать все, что угодно. Или, как любила говорить Айн Рэнд: «Каковы ваши предпосылки?»

Это не беспокоило Лейбница, для которого не существовало математической логической системы, и который был полностью уверен и доволен рационалистической уверенностью в том, что все предпосылки его мысли были самоочевидными истинами.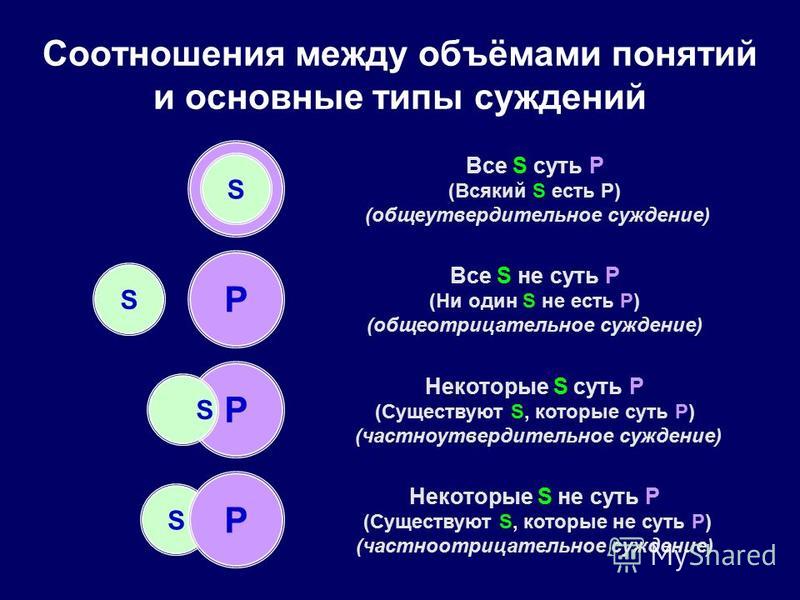 Это все еще было наследием Аристотеля. Крах рационализма в критике Юма и Канта поставил позитивистов в затруднительное положение. Они не могли апеллировать к самоочевидным истинам, кроме как в логике; и их непреклонное преклонение перед наукой не полностью закрыло им глаза на Проблему индукции, которую использовал Юм в качестве оружия. Так что же им было делать со своими предпосылками, своими Первыми принципами? Evasion , кажется, был ответом. Это было сделано либо из-за путаницы, либо из-за нечестности, которые могли быть объединены в смесь самообмана и высокомерия.

«Уклонение», конечно же, означало, что в аргументы тайно использовались необоснованные, бесспорные и неисследованные предпосылки. У позитивистов это обычно было связано с логикой, значением и языком, так что излюбленное отклонение позитивистами предложений, например, в этике или метафизике, было то, что они были связаны с «неправильным использованием языка». Основа или происхождение их авторитетного и нормативного знания языка замалчивались. А поскольку они плохо понимали естественные языки, их утверждения о языке обычно были необоснованными и часто абсурдными.Когда я попытался записаться на курс философии языка в Калифорнийском университете в Лос-Анджелесе в 1968 году, и профессор сказал, что «языком», которым он будет заниматься в этой четверти, будет математика , я понял, что не извлечу ничего ценного из этого класса. Я хотел спросить профессора, как можно спросить: «А где ванная?» на «языке» математики. Очевидно, что академическим философам не нужно спрашивать о ванных комнатах.

Даже когда Витгенштейн нападал на многие принципы логического позитивизма, он продолжал придерживаться подхода, согласно которому его собственное особое, уникальное, нормативное и открывающее понимание сущности языка — в мире, по его словам, без сущностей — позволил ему разрешить все вопросы философии — в основном отбросить их, как это делали позитивисты, как бессмысленные не вопросы.Ответ на один вид нигилизма другим не кажется мне чем-то существенным.

Итак, прославленные современные философы и их школы до сих пор не знают, что делать с предпосылками и Первыми принципами. Вместо того, чтобы позволять им их уклонения, мы можем начать с Аристотеля. Приведенная ниже диаграмма графически представляет взгляд Аристотеля на то, как производятся знания.

Наша попытка логически обосновать наши убеждения, приводя доводы, приводит к «регрессу причин».»Поскольку любая причина может быть дополнительно оспорена, регресс причин грозит бесконечным регрессом. Однако, поскольку это невозможно, должны быть причины, для которых не требуется дополнительных причин: причины, которые не нужно доказывать . По определению, это «первые принципы» (ἀρχαί, Principia prima ) или «первые принципы демонстрации» ( Principia prima manifestrationis ). «Проблема первых принципов» возникает, когда мы спрашиваем: Почему такие причины не нужно доказывать.Ответ Аристотеля заключался в том, что первые принципы не нуждаются в доказательстве, потому что они самоочевидны, , то есть, как известно, они истинны, просто понимая их.

Но Аристотель считает, что знание начинается с опыта. Мы добираемся до первых принципов посредством индукции. Но в обобщениях индукции нет уверенности. «Проблема индукции» — это вопрос Как мы узнаем, когда мы изучили достаточно отдельных случаев, чтобы сделать индуктивное обобщение.Обычно мы не можем знать.

Таким образом, чтобы перейти от неопределенности индуктивных обобщений к достоверности самоочевидных первых принципов, должен быть интуитивный «скачок», через то, что Аристотель называет «Разумом» (νοῦς, noûs ). Это связывает систему воедино. . Дедуктивная система из первых принципов (например, евклидова геометрия) — это то, что Аристотель называет «знанием» (ἐπιστήμη, eptemê по-гречески или scientia по-латыни). Рационалисты , такие как Декарт, Спиноза и Лейбниц, позже считали, что часть системы с очевидными первыми принципами и дедукцией — это все, что необходимо для философии.

Самоочевидность не подходит для решения проблемы первых принципов, потому что нет способа разрешить споры о том, является ли что-то самоочевидным или нет. Область самоочевидного резко сужается Юмом и Кантом. Эмпирики , такие как Локк, Беркли и Юм, считали, что знание — это в основном вопрос индукции. Однако Юм обострил проблему индукции, отметив, что никакие обобщения не являются логически обоснованными.Таким образом, эмпирическая традиция достигла высшей точки в скептицизме, заключении Юма о том, что знания в традиционном смысле не существует. Рационалисты, в свою очередь, были смущены тем, что их системы, предположительно основанные на самоочевидных истинах, тем не менее, противоречат друг другу. Символично, что отдельные ветви арки без краеугольного камня самоочевидности явно нестабильны и не могут стоять самостоятельно.

Кант предложил другое решение проблемы первых принципов: синтетические предложения a priori являются первыми принципами демонстрации, но не самоочевидны.Фрис добавил, что они вообще не были известны интуитивно. Наконец, Карл Поппер разрешает регресс причин, по крайней мере, для научного метода, заменяя проверку фальсификацией. Но оказывается, что это также применимо и к сократовскому методу.

Основы ценности, логические вопросы

Аристотелевские силлогизмы

В защиту Брамантип

Основы ценности, эпистемологические проблемы

Фризская трилемма

Трилеммы Мюнхгаузена и Локка

Основы ценностей, метафизические вопросы

Эпистемология

История философии

Домашняя страница

Как Аристотель создал компьютер

ИСТОРИЯ Компьютеров часто рассказывают как историю объектов, от счетчиков до машины Бэббиджа и машин для взлома кодов времен Второй мировой войны. Фактически, это лучше понимать как историю идей, в основном идей, которые возникли из математической логики, малоизвестной и культовой дисциплины, которая впервые возникла в 19 веке. Пионерами математической логики стали философы-математики, в первую очередь Джордж Буль и Готлоб Фреге, которые сами были вдохновлены мечтой Лейбница об универсальном «языке понятий» и древней логической системой Аристотеля.

Прослушайте аудиоверсию этой статьи: Особые истории, прочтите вслух: загрузите приложение Audm для своего iPhone.
Математическая логика изначально считалась безнадежно абстрактным предметом, не имеющим мыслимых приложений. Как прокомментировал один компьютерный ученый: «Если бы в 1901 году талантливому и отзывчивому стороннему наблюдателю пришлось бы исследовать науку и назвать отрасль, которая была бы наименее плодотворной в [] столетие вперед, его выбор вполне мог бы остановиться на математической логике. .И тем не менее, это обеспечит основу для области, которая окажет большее влияние на современный мир, чем любая другая.
Развитие информатики из математической логики завершилось в 1930-х годах двумя знаковыми статьями: «Символьный анализ коммутационных и релейных схем» Клода Шеннона и «О вычислимых числах в приложении Entscheidungsproblem » Алана Тьюринга. ” В истории информатики Шеннон и Тьюринг — выдающиеся личности, но важность предшествовавших им философов и логиков часто упускается из виду.
В хорошо известной истории компьютерных наук статья Шеннона описывается как «возможно, самая важная, а также самая известная магистерская диссертация века». Шеннон написал ее, будучи студентом-электротехником в Массачусетском технологическом институте. Его советник Ванневар Буш построил прототип компьютера, известного как дифференциальный анализатор, который мог быстро вычислять дифференциальные уравнения. Устройство было в основном механическим, с подсистемами, управляемыми электрическими реле, которые были организованы специальным образом, поскольку еще не существовало систематической теории, лежащей в основе проектирования схем.Тема диссертации Шеннона возникла, когда Буш порекомендовал ему попытаться открыть такую теорию.
«Математику можно определить как предмет, в котором мы никогда не знаем, о чем говорим».
Статья Шеннона во многом является типичной статьей по электротехнике, наполненной уравнениями и диаграммами электрических цепей. Что необычно, так это то, что в первую очередь ссылались на работу по математической философии Джорджа Буля «Законы мышления », написанную 90 лет назад.
Сегодня имя Буля хорошо известно компьютерщикам (многие языки программирования имеют базовый тип данных, называемый логическим), но в 1938 году его редко читали за пределами философских факультетов.Сам Шеннон познакомился с работами Буля на студенческом курсе философии. «Просто так получилось, что никто другой не был знаком с обоими месторождениями одновременно», — комментировал он позже.
Буля часто называют математиком, но он видел себя философом, идущим по стопам Аристотеля. Законы мысли начинается с описания его целей — исследования фундаментальных законов работы человеческого разума:
Цель следующего трактата — исследовать фундаментальные законы тех операций разума, с помощью которых рассуждение проводится; дать им выражение на символическом языке исчисления и на этом основании основать науку логики…. и, наконец, собрать … некоторые вероятные сведения о природе и строении человеческого разума.
Затем он отдает дань уважения Аристотелю, изобретателю логики, и первостепенному влиянию на его собственные работы:
Действительно, в своей древней схоластической форме предмет логики почти исключительно связан с великим именем Аристотеля. . Поскольку он был представлен Древней Греции в частично технических, частично метафизических исследованиях T he Organon , то без каких-либо существенных изменений он сохранился до наших дней.
Попытка улучшить логическую работу Аристотеля была интеллектуально смелым шагом. Логика Аристотеля, представленная в его книге « Органон » из шести частей, более 2000 лет занимала центральное место в научном каноне. Было широко распространено мнение, что Аристотель написал почти все, что можно было сказать по этой теме. Великий философ Иммануил Кант заметил, что со времен Аристотеля логика «не могла сделать ни единого шага вперед, и поэтому, по всей видимости, она кажется законченной и законченной.
Центральное наблюдение Аристотеля заключалось в том, что аргументы действительны или не основаны на их логической структуре, независимо от используемых нелогических слов. Самая известная схема аргументов, которую он обсуждал, известна как силлогизм:
Все люди смертны.
Сократ — мужчина.
Следовательно, Сократ смертен.
Вы можете заменить «Сократ» любым другим объектом, а «смертный» — любым другим предикатом, и аргумент останется в силе. Достоверность аргумента определяется исключительно логической структурой.Логические слова — «все», «есть», «есть» и «поэтому» — делают всю работу.
Аристотель также определил набор основных аксиом, из которых он вывел остальную часть своей логической системы:
Объект — это то, что он есть (Закон тождества)
Никакое утверждение не может быть одновременно истинным и ложным (Закон не- противоречие)
Каждое утверждение истинно или ложно (Закон исключенного среднего)
Эти аксиомы были предназначены не для описания того, как люди на самом деле думают (это было бы областью психологии), но как идеализированное, совершенно рациональное человек должен думать.
Аксиоматический метод Аристотеля повлиял на еще более известную книгу Евклида Elements , которая, по оценкам, уступает только Библии по количеству напечатанных изданий.
Фрагмент Elements (Wikimedia Commons)
Хотя якобы о геометрии, Elements стал стандартным учебником для обучения строгому дедуктивному мышлению. (Авраам Линкольн однажды сказал, что он научился здравой правовой аргументации, изучая Евклида.) В системе Евклида геометрические идеи были представлены в виде пространственных диаграмм.Так продолжали практиковаться в геометрии, пока Рене Декарт в 1630-х годах не показал, что вместо этого геометрию можно представить в виде формул. Его «Рассуждение о методе » было первым учебником по математике на Западе, который популяризировал то, что сейчас является стандартным алгебраическим обозначением — x, y, z для переменных, a, b, c для известных величин и так далее.
Алгебра Декарта позволила математикам выйти за рамки пространственной интуиции и манипулировать символами, используя точно определенные формальные правила. Это сместило доминирующий вид математики с диаграмм на формулы, что привело, среди прочего, к развитию исчисления, изобретенного примерно через 30 лет после Декарта, независимо Исааком Ньютоном и Готфридом Лейбницем.
Целью Буля было сделать для логики Аристотеля то, что Декарт сделал для евклидовой геометрии: освободить ее от ограничений человеческой интуиции, придав ей точную алгебраическую нотацию. Приведу простой пример, когда Аристотель писал:
Все люди смертны.
Boole заменил слова «мужчины» и «смертные» на переменные, а логические слова «all» и «are» — на арифметические операторы:
x = x * y
Что можно интерпретировать как « Все в наборе x также есть в наборе y .
законов мысли создал новую научную область — математическую логику, которая в последующие годы стала одной из самых активных областей исследований математиков и философов. Бертран Рассел назвал « законов мысли » «работой, в которой была открыта чистая математика».
Шеннон понял, что систему Буля можно отображать непосредственно на электрические цепи. В то время электрические схемы не имели систематической теории, регулирующей их конструкцию. Шеннон понял, что правильная теория будет «в точности аналогична исчислению предложений, используемому в символическом изучении логики».
Он показал соответствие между электрическими цепями и булевыми операциями в простой диаграмме:
Отображение Шеннона электрических цепей в символическую логику (Университет Вирджинии)
Это соответствие позволило компьютерным ученым перенести десятилетия работы по логике и математике Буля и последующих логики. Во второй половине своей статьи Шеннон показал, как булеву логику можно использовать для создания схемы для сложения двух двоичных цифр.
Сумматор Шеннона (Университет Вирджинии, )
Соединяя эти схемы сумматора вместе, можно было построить произвольно сложные арифметические операции. Эти схемы станут основными строительными блоками того, что сейчас известно как арифметические логические блоки, ключевого компонента современных компьютеров.
Еще один способ охарактеризовать достижения Шеннона состоит в том, что он первым различил компьютеры логического уровня и физического уровня компьютеров. (Это различие стало настолько фундаментальным для информатики, что современным читателям может показаться удивительным, насколько проницательным оно было в то время — напоминание о пословице о том, что «философия одного века — это здравый смысл следующего».)
Со времени публикации статьи Шеннона на физическом уровне компьютеров был достигнут огромный прогресс, включая изобретение транзистора в 1947 году Уильямом Шокли и его коллегами из Bell Labs. Транзисторы представляют собой значительно улучшенные версии электрических реле Шеннона — наиболее известного способа физического кодирования логических операций.В течение следующих 70 лет полупроводниковая промышленность упаковывала все больше и больше транзисторов в меньшие пространства. В iPhone 2016 года около 3,3 миллиарда транзисторов, каждый из которых представляет собой «релейный переключатель», как те, что изображены на диаграммах Шеннона.
В то время как Шеннон показал, как отображать логику в физическом мире, Тьюринг показал, как проектировать компьютеры на языке математической логики. Когда Тьюринг писал свою статью в 1936 году, он пытался решить «проблему принятия решения», впервые идентифицированную математиком Дэвидом Гильбертом, который спросил, существует ли алгоритм, который мог бы определить, истинно или ложно произвольное математическое утверждение.В отличие от статьи Шеннона, статья Тьюринга носит сугубо технический характер. Его основное историческое значение заключается не в ответе на проблему принятия решения, а в шаблоне для компьютерного дизайна, который он предоставил по ходу дела.
Тьюринг работал в традициях, восходящих к Готфриду Лейбницу, философскому гиганту, который разработал исчисление независимо от Ньютона. Среди множества вкладов Лейбница в современную мысль одной из самых интригующих была идея нового языка, который он назвал «универсальной характеристикой», который, как он представлял, может представлять все возможные математические и научные знания.Частично вдохновленный религиозным философом 13-го века Рамоном Лулллом, Лейбниц предположил, что язык будет идеографическим, как египетские иероглифы, за исключением того, что символы будут соответствовать «атомарным» концепциям математики и естествознания. Он утверждал, что этот язык даст человечеству «инструмент», который может усилить человеческий разум «в гораздо большей степени, чем оптические инструменты», такие как микроскоп и телескоп.
Он также вообразил машину, которая может обрабатывать язык, которую он назвал логическим вычислителем.
Если бы возникли разногласия, не было бы необходимости в диспуте между двумя философами больше, чем между двумя бухгалтерами. Ибо достаточно было бы взять их карандаши в руки и сказать друг другу: Calculemus — Давайте посчитаем.
Лейбниц не получил возможности разработать свой универсальный язык или соответствующую машину (хотя он действительно изобрел относительно простую вычислительную машину, ступенчатый счетчик). Первая убедительная попытка осуществить мечту Лейбница была предпринята в 1879 году, когда немецкий философ Готлоб Фреге опубликовал свой исторический трактат по логике Begriffsschrift . Вдохновленный попыткой Буля улучшить логику Аристотеля, Фреге разработал гораздо более совершенную логическую систему. Логика, которую сегодня преподают на курсах философии и информатики — логика первого порядка или логика предикатов — является лишь небольшой модификацией системы Фреге.
Фреге считается одним из самых выдающихся философов XIX века. Среди прочего, ему приписывают катализатор того, что известный философ Ричард Рорти назвал «лингвистическим поворотом» в философии. Поскольку философия Просвещения была одержима вопросами знания, философия после Фреге стала одержима вопросами языка.Среди его учеников были два самых важных философа 20 века — Бертран Рассел и Людвиг Витгенштейн.
Главное нововведение логики Фреге состоит в том, что она гораздо точнее представляет логическую структуру обычного языка. Среди прочего, Фреге был первым, кто использовал кванторы («для каждого», «существует») и для отделения объектов от предикатов. Он также был первым, кто разработал то, что сегодня является фундаментальными концепциями в информатике, такими как рекурсивные функции и переменные с областью видимости и привязкой.
Формальный язык Фреге — то, что он назвал своим «концептуальным сценарием» — состоит из бессмысленных символов, которыми манипулируют по четко определенным правилам. Языку придается значение только посредством интерпретации, которая указывается отдельно (это различие позже будет названо синтаксисом по сравнению с семантикой). Это превратило логику в то, что выдающиеся компьютерные ученые Аллан Ньюэлл и Герберт Саймон назвали «символьной игрой», «в которую играют бессмысленными токенами по определенным чисто синтаксическим правилам.
Все смыслы были очищены. У одного была механическая система, относительно которой можно было доказать разные вещи. Таким образом, прогресс был сначала достигнут путем отхода от всего, что казалось относящимся к значению и человеческим символам.
Как заметил Бертран Рассел: «Математику можно определить как предмет, в котором мы никогда не узнаем, о чем говорим, и не знаем, правда ли то, что мы говорим».
Неожиданным следствием работы Фреге стало обнаружение слабых мест в основах математики. Например, книга Евклида « элементов» — , считавшаяся золотым стандартом логической строгости в течение тысяч лет — оказалась полна логических ошибок. Поскольку Евклид использовал обычные слова, такие как «линия» и «точка», он — и столетия читателей — обманывали себя, делая предположения о предложениях, содержащих эти слова. Приведу один относительно простой пример: в обычном использовании слово «линия» подразумевает, что если вам даны три различные точки на линии, одна точка должна находиться между двумя другими.Но когда вы определяете «линию», используя формальную логику, оказывается, что «промежуточность» также должна быть определена — то, что Евклид упустил из виду. Формальная логика позволяет легко обнаружить подобные пробелы.
Осознание этого привело к кризису в основах математики. Если Elements — библия математики — содержали логические ошибки, то в каких других областях математики тоже? А как насчет таких наук, как физика, которые были построены на основе математики?
Хорошая новость заключается в том, что те же логические методы, которые использовались для обнаружения этих ошибок, также можно использовать для их исправления. Математики начали восстанавливать основы математики снизу вверх. В 1889 году Джузеппе Пеано разработал аксиомы для арифметики, а в 1899 году Давид Гильберт сделал то же самое для геометрии. Гильберт также изложил программу формализации оставшейся части математики с особыми требованиями, которым должна удовлетворять любая такая попытка, в том числе:
Полнота: Должно быть доказательство того, что все истинные математические утверждения могут быть доказаны в формальной системе.
Разрешимость: Должен существовать алгоритм для определения истинности или ложности любого математического утверждения.(Это « Entscheidungsproblem » или «проблема решения», о которой упоминается в статье Тьюринга.)
Перестройка математики таким образом, чтобы удовлетворять этим требованиям, стала известна как программа Гильберта. Вплоть до 1930-х годов это было в центре внимания основной группы логиков, включая Гильберта, Рассела, Курта Гёделя, Джона фон Неймана, Алонзо Черча и, конечно же, Алана Тьюринга.
«В науке новизна возникает с трудом».
Программа Гильберта действовала по крайней мере на двух фронтах.На первом этапе логики создали логические системы, которые пытались доказать, что требования Гильберта выполняются или нет.
На втором фронте математики использовали логические концепции для восстановления классической математики. Например, арифметическая система Пеано начинается с простой функции, называемой функцией-преемником, которая увеличивает любое число на единицу. Он использует функцию-преемник для рекурсивного определения сложения, использует сложение для рекурсивного определения умножения и так далее, пока не будут определены все операции теории чисел.Затем он использует эти определения вместе с формальной логикой для доказательства теорем об арифметике.
Историк Томас Кун однажды заметил, что «в науке новизна возникает с трудом». В эпоху программы Гильберта логика представляла собой бурный процесс созидания и разрушения. Один логик построил бы сложную систему, а другой разрушил бы ее.
Излюбленным орудием разрушения было построение самореферентных, парадоксальных утверждений, показывающих, что аксиомы, из которых они были выведены, непоследовательны.Простая форма этого «парадокса лжеца» — это предложение:
Это предложение неверно.
Если это правда, то это ложь, а если ложь, то это правда, что ведет к бесконечной петле внутреннего противоречия.
Рассел первым заметным образом применил парадокс лжеца в математической логике. Он показал, что система Фреге позволяет выводить противоречащие друг другу множества:
Пусть R будет набором всех множеств, которые не являются членами самих себя. Если R не является членом самого себя, то его определение требует, чтобы он содержал себя, а если он содержит себя, то он противоречит своему собственному определению как совокупность всех множеств, которые не являются членами самих себя.
Это стало известно как парадокс Рассела и рассматривалось как серьезный изъян в достижении Фреге. (Сам Фреге был шокирован этим открытием. Он ответил Расселу: «Ваше открытие противоречия вызвало у меня величайшее удивление и, я бы сказал, испуг, поскольку оно пошатнуло основу, на которой я намеревался строить свою арифметику». )
Рассел и его коллега Альфред Норт Уайтхед предприняли наиболее амбициозную попытку дополнить программу Гильберта «Принципами математики , », опубликованными в трех томах между 1910 и 1913 годами . Метод компании Principia был настолько подробным, что потребовалось более 300 страниц, чтобы получить доказательство того, что 1 + 1 = 2.
Рассел и Уайтхед пытались разрешить парадокс Фреге, представив то, что они назвали теорией типов. Идея заключалась в том, чтобы разделить формальные языки на несколько уровней или типов. Каждый уровень может относиться к уровням ниже, но не к их собственным или более высоким уровням. Это разрешило парадоксы самоотнесения, фактически запретив самореференцию. (Это решение не было популярным среди логиков, но оно повлияло на информатику — большинство современных компьютерных языков имеют функции, вдохновленные теорией типов. )
Парадоксы самореференции в конечном итоге показали, что программа Гильберта никогда не может быть успешной. Первый удар был нанесен в 1931 году, когда Гёдель опубликовал свою теперь знаменитую теорему о неполноте, которая доказала, что любая последовательная логическая система, достаточно мощная, чтобы охватить арифметику, также должна содержать утверждения, которые верны, но не могут быть доказаны. (Теорема Гёделя о неполноте — один из немногих логических результатов, получивших широкую популяризацию благодаря таким книгам, как Gödel, Escher, Bach и The Emperor’s New Mind).
Последний удар был нанесен, когда Тьюринг и Алонзо Черч независимо друг от друга доказали, что не может существовать никакого алгоритма, определяющего, истинно или ложно произвольное математическое утверждение. (Черч сделал это, изобретя совершенно другую систему, названную лямбда-исчислением, которая позже вдохновила компьютерные языки, такие как Лисп.) Ответ на проблему принятия решения был отрицательным.
Ключевое открытие Тьюринга было сделано в первом разделе его знаменитой статьи 1936 года «О вычислимых числах в приложении к задаче Entscheidungsproblem ».Чтобы строго сформулировать задачу решения (« Entscheidungsproblem »), Тьюринг сначала создал математическую модель того, что значит быть компьютером (сегодня машины, которые соответствуют этой модели, известны как «универсальные машины Тьюринга»). Логик Мартин Дэвис описывает это:
Тьюринг знал, что алгоритм обычно определяется списком правил, которым человек может следовать точным механическим способом, как рецепт в кулинарной книге. Он смог показать, что такой человек может быть ограничен несколькими чрезвычайно простыми базовыми действиями без изменения конечного результата вычислений.
Затем, доказав, что никакая машина, выполняющая только эти базовые действия, не может определить, следует ли данный предложенный вывод из заданных посылок с использованием правил Фреге, он смог сделать вывод, что не существует алгоритма для задачи Entscheidungsproblem .
В качестве побочного продукта он нашел математическую модель универсальной вычислительной машины.
Затем Тьюринг показал, как программа может храниться внутри компьютера вместе с данными, с которыми она работает.Используя современный словарь, мы бы сказали, что он изобрел архитектуру «хранимых программ», которая лежит в основе большинства современных компьютеров:
До Тьюринга общее предположение заключалось в том, что при работе с такими машинами три категории — машины, программы и данные. — были совершенно отдельными образованиями. Машина была физическим объектом; сегодня мы бы назвали это оборудованием. Программа была планом выполнения вычислений, возможно, воплощенных в перфокартах или соединениях кабелей на коммутационной плате. Наконец, данные были числовым вводом.Универсальная машина Тьюринга показала, что различие этих трех категорий является иллюзией.
Это была первая строгая демонстрация того, что любую вычислительную логику, которая может быть закодирована аппаратно, можно также закодировать программно. Архитектура, описанная Тьюрингом, позже была названа «архитектурой фон Неймана» — но современные историки в целом согласны с тем, что она пришла из Тьюринга, как, по-видимому, сам фон Нейман.
Хотя на техническом уровне программа Гильберта потерпела неудачу, усилия на этом пути продемонстрировали, что большие области математики могут быть построены с помощью логики.А после идей Шеннона и Тьюринга, показывающих связи между электроникой, логикой и вычислениями, появилась возможность экспортировать этот новый концептуальный механизм в компьютерный дизайн.
Во время Второй мировой войны эта теоретическая работа была реализована на практике, когда правительственные лаборатории наняли ряд элитных логиков. Фон Нейман присоединился к проекту атомной бомбы в Лос-Аламосе, где он работал над компьютерным дизайном для поддержки физических исследований. В 1945 году он написал спецификацию EDVAC — первого логического компьютера с хранимой программой, который обычно считается исчерпывающим справочником по источникам для современного компьютерного дизайна.
Тьюринг присоединился к секретному подразделению в Блетчли-парке, к северо-западу от Лондона, где он помогал проектировать компьютеры, которые сыграли важную роль в взломе немецких кодов. Самым большим его вкладом в практический компьютерный дизайн была его спецификация ACE, или Automatic Computing Engine.
Будучи первыми компьютерами, основанными на логической логике и архитектурах хранимых программ, ACE и EDVAC во многом были похожи. Но у них также были интересные различия, некоторые из которых предвещали современные дискуссии в области компьютерного дизайна.Излюбленные дизайны фон Неймана были похожи на современные процессоры CISC («сложные»), воплощая богатую функциональность в аппаратное обеспечение. Дизайн Тьюринга больше походил на современные RISC («сокращенные») процессоры, сводя к минимуму сложность оборудования и передавая больше работы программному обеспечению.
Фон Нейман считал, что программирование компьютеров будет утомительной канцелярской работой. Тьюринг, напротив, сказал, что компьютерное программирование «должно быть очень увлекательным. Нет никакой реальной опасности, что он когда-либо превратится в рутину, поскольку любые процессы, которые являются достаточно механическими, могут быть переданы самой машине.”
С 1940-х годов компьютерное программирование значительно усложнилось. Одна вещь, которая не изменилась, — это то, что она по-прежнему состоит в основном из программистов, определяющих правила, которым должны следовать компьютеры. С философской точки зрения мы бы сказали, что компьютерное программирование следует традиции дедуктивной логики, ветви логики, о которой говорилось выше, которая имеет дело с манипуляциями с символами в соответствии с формальными правилами.
Примерно за последнее десятилетие программирование начало меняться с ростом популярности машинного обучения, которое включает создание структур для обучения машин с помощью статистических выводов.Это приблизило программирование к другой основной ветви логики, индуктивной логике, которая имеет дело с выводом правил из конкретных примеров.
Сегодняшние самые многообещающие методы машинного обучения используют нейронные сети, которые были впервые изобретены в 1940-х годах Уорреном Маккалоком и Уолтером Питтсом, чьей идеей было разработать исчисление для нейронов, которое можно было бы, подобно булевой логике, использовать для построения компьютерных схем. Нейронные сети оставались эзотерическими до тех пор, пока спустя десятилетия они не были объединены со статистическими методами, которые позволили им совершенствоваться по мере поступления большего количества данных.В последнее время, когда компьютеры стали все более искусными в обработке больших наборов данных, эти методы дали замечательные результаты. Программирование в будущем, вероятно, будет означать раскрытие нейронных сетей миру и предоставление им возможности учиться.
Это был бы подходящий второй акт в истории компьютеров. Логика зародилась как способ понять законы мышления. Затем это помогло создать машины, которые могли рассуждать в соответствии с правилами дедуктивной логики. Сегодня дедуктивная и индуктивная логика объединяются для создания машин, которые одновременно рассуждают и обучаются.То, что началось, по словам Буля, с исследования, «касающегося природы и строения человеческого разума», могло привести к созданию новых умов — искусственных умов, — которые когда-нибудь могут сравниться с нашим собственным или даже превзойти его.
Аристотелевская логика — TeacherVision

Было бы трудно обсуждать логические рассуждения без упоминания Аристотеля. Греческий философ, живший с 384 по 322 год до нашей эры, Аристотель был учеником Платона и основателем того, что мы сегодня знаем как формальную логику .

Большая часть произведений Аристотеля утеряна, но его ученики и последующие ученые написали множество комментариев, основанных на его учениях. Группа его трактатов была собрана под названием Органон , что означает «инструмент». Вместо того, чтобы представлять логику как дисциплину, Аристотель считал ее инструментом философского рассуждения. Модель Organon состояла из шести частей: Категории , Об интерпретации , Предварительная аналитика , Последующая аналитика , Темы и Софистические опровержения .

Аристотель утверждал, что все знания должны быть получены из того, что уже известно, и поэтому его логика была сосредоточена вокруг типа мышления, называемого дедукция . Используя дедукцию, вы начинаете с заданного набора правил и условий и определяете, что должно быть истинным, как следствие. Процитируя Prior Analytics , «дедукция — это речь, в которой, при предположении определенных вещей, нечто отличное от этих [вещей] предполагалось как результат необходимости из-за того, что они таковы.«Предполагаемые вещи» — это предпосылки, а «нечто отличное от предполагаемых» — выводы.

Основная форма этого метода рассуждения стала известна как силлогизм . Силлогизмы — это структурированные предложения (называемые утверждениями ) которые являются либо истинными, либо ложными; они должны содержать предикат субъекта и предикат и должны либо подтверждать, либо опровергать предикат субъекта. Другими словами, это предложения, утверждающие, что одно понятие должно или не должно вытекать из Другая.Возможно, вы даже знакомы с этой формой:

Если A основано на всех B ,
и B основано на всех C ,
тогда A основано на всех C .

Знаменитый пример Аристотеля гласит:
Если все люди смертны,
и все греки — люди
, то все греки смертны.
Вы часто можете встретить этот тип утверждения «Если … то» в математических доказательствах, и это связано с далеко идущим влиянием аристотелевских методов.Они изменили облик научной мысли в свое время и в течение почти 2000 лет после этого позволяли делать выводы о новых истинах на основе установленных фактов или принципов. Если бы вы могли переводить аргументы в силлогизмы, тогда вы могли бы предсказывать новые результаты или последствия, будь то в математике, естествознании или философии. Только в прошлом веке методы Аристотеля подверглись сомнению такими учеными, как Готлоб Фреге и Бертран Рассел. Были разработаны новые типы логики, обеспечивающие более точную основу для математических и научных исследований.Однако важность работ Аристотеля никогда не будет забыта.
Платоновское деление и истоки аристотелевской логики
Abstract
Силлогистическая теория Аристотеля, развитая в его «Априорной аналитике», часто рассматривается как рождение логики в западной философии. В течение последнего столетия ученые пытались определить важных предшественников этой теории. Я утверждаю, что платоновское деление, метод, который направлен на объяснение сущностей естественных видов путем постепенного сужения от рода, повлиял на логическую теорию Аристотеля во многих важных аспектах.Чтобы понять, как именно, я анализирую метод деления в том виде, в каком он был первоначально задуман Платоном и принят Аристотелем. Я утверждаю, что, хотя Платон допускал, что некоторые подразделения не могут строго исследовать сущность, он начал программу, продолженную Аристотелем (и другими в древности и средневековье), по поиску норм разделения, которые могли бы применяться в любой области. Идея строгого общего метода была подхвачена и развита Аристотелем в его силлогистике. Аристотель также использовал платоновскую концепцию предикации как части в своей семантике силлогистических суждений.В рамках своей аргументации я доказываю, что семантика, основанная на платоновских разделительных структурах, является правильной и полной для системы дедукции, используемой в литературе для моделирования силлогистики Аристотеля.
Основное содержание
Загрузить PDF для просмотраПросмотреть больше

Дополнительная информация Меньше информации
Закрывать
Введите пароль, чтобы открыть этот PDF-файл:
Отмена В ПОРЯДКЕ
Подготовка документа к печати…
Отмена
3: Дедуктивная логика I — Аристотелевская логика
Последнее обновление
Сохранить как PDF
Без заголовков
В этой и следующей главах мы изучим две дедуктивные логики — два подхода к оценке дедуктивных аргументов. Первый, который является предметом настоящей главы, был разработан Аристотелем почти 2500 лет назад, и мы будем называть его просто аристотелевской логикой; вторая, тема следующей главы, имеет почти такие же древние корни, как у Аристотеля, но не была полностью развита до XIX века и называется сентенциальной логикой.
3.1: Дедуктивная логика
В этой и следующей главах мы изучим две дедуктивные логики — два подхода к оценке дедуктивных аргументов.Первый, который является предметом настоящей главы, был разработан Аристотелем почти 2500 лет назад, и мы будем называть его просто аристотелевской логикой; вторая, тема следующей главы, имеет почти такие же древние корни, как у Аристотеля, но не была полностью развита до XIX века и называется сентенциальной логикой.
3.2: Классы и категориальные предложения
Для Аристотеля фундаментальной логической единицей является класс. Классы — это просто наборы вещей, которые мы можем выделить с помощью языка. Самый простой способ идентифицировать класс — использовать существительное во множественном числе: деревья, облака, астероиды, люди — это все классы. Имена классов могут быть более сложными с грамматической точки зрения. Мы можем заменить существительное во множественном числе прилагательным: «богатые люди» выделяют класс.
3.3: Квадрат оппозиции
Четыре типа категорий систематически связаны друг с другом; мы посмотрим на эти отношения. Отношения являются логическими: мы часто можем сделать вывод, например, из истинности одного из четырех категориальных, являются ли остальные три истинными или ложными.Эти умозаключительные отношения между четырьмя категориальными предложениями графически резюмируются в Квадрате оппозиции.
3.4: Операции над категориальными предложениями
Мы продолжаем исследование той части естественного языка, которой ограничивается логика Аристотеля, — предложений стандартной формы, выражающих категориальные предложения. Чтобы ближе познакомиться с ними, мы рассмотрим, как они реагируют, когда мы выполняем с ними различные операции, когда мы манипулируем ими различными способами.Мы рассмотрим три операции: преобразование, противодействие и противопоставление. Каждый из них каким-то образом изменяет предложения стандартной формы.
3.5: Проблемы с квадратом оппозиции
Квадрат оппозиции — чрезвычайно полезный инструмент: он аккуратно резюмирует в графической форме все, что мы знаем о взаимосвязях между четырьмя типами категориальных утверждений.
3.6: Категорические силлогизмы
Как мы уже сказали, аристотелевская логика ограничивается оценкой аргументов, все утверждения которых — предпосылки и заключения — категоричны.Есть еще одно ограничение: аристотелевская логика оценивает только категориальные силлогизмы. Это особый вид аргументации, отвечающий следующим условиям: категорический силлогизм — это дедуктивный аргумент, состоящий из трех категориальных предложений (двух посылок и заключения).