10 занимательных логических парадоксов

Учёные и мыслители с давних времён любят развлекать себя и коллег постановкой неразрешимых задач и формулированием разного рода парадоксов. Некоторые из подобных мысленных экспериментов сохраняют актуальность на протяжении тысяч лет, что свидетельствует о несовершенстве многих популярных научных моделей и «дырах» в общепринятых теориях, давно считающихся фундаментальными. Предлагаем вам поразмыслить над наиболее интересными и удивительными парадоксами, которые, как сейчас выражаются, «взорвали мозг» не одному поколению логиков, философов и математиков.

1. Апория «Ахиллес и черепаха»

Парадокс Ахиллеса и черепахи — одна из апорий (логически верных, но противоречивых высказываний), сформулированных древнегреческим философом Зеноном Элейским в V-м веке до нашей эры. Суть её в следующем: легендарный герой Ахиллес решил посоревноваться в беге с черепахой. Как известно, черепахи не отличаются прыткостью, поэтому Ахиллес дал сопернику фору в 500 м. Когда черепаха преодолевает эту дистанцию, герой пускается в погоню со скоростью в 10 раз большей, то есть пока черепаха ползёт 50 м, Ахиллес успевает пробежать данные ей 500 м форы. Затем бегун преодолевает следующие 50 м, но черепаха в это время отползает ещё на 5 м, кажется, что Ахиллес вот-вот её догонит, однако соперница всё ещё впереди и пока он бежит 5 м, ей удаётся продвинуться ещё на полметра и так далее. Дистанция между ними бесконечно сокращается, но по идее, герою так и не удаётся догнать медлительную черепаху, она ненамного, но всегда опережает его.

© www.student31.ru

Конечно, с точки зрения физики парадокс не имеет смысла — если Ахиллес движется намного быстрее, он в любом случае вырвется вперёд, однако Зенон, в первую очередь, хотел продемонстрировать своими рассуждениями, что идеализированные математические понятия «точка пространства» и «момент времени» не слишком подходят для корректного применения к реальному движению. Апория выявляет расхождение между математически обоснованной идеей, что ненулевые интервалы пространства и времени можно делить бесконечно (поэтому черепаха должна всегда оставаться впереди) и реальностью, в которой герой, конечно, выигрывает гонку.

2. Парадокс временной петли

«Новые путешественники во времени» Дэвида Туми

Парадоксы, описывающие путешествия во времени, давно служат источником вдохновения для писателей-фантастов и создателей научно-фантастических фильмов и сериалов. Существует несколько вариантов парадоксов временной петли, один из самых простых и наглядных примеров подобной проблемы привёл в своей книге «The New Time Travelers» («Новые путешественники во времени») Дэвид Туми, профессор из Университета Массачусетса.

Представьте себе, что путешественник во времени купил в книжном магазине экземпляр шекспировского «Гамлета». Затем он отправился в Англию времён Королевы-девы Елизаветы I и отыскав Уильяма Шекспира, вручил ему книгу. Тот переписал её и издал, как собственное сочинение. Проходят сотни лет, «Гамлета» переводят на десятки языков, бесконечно переиздают, и одна из копий оказывается в том самом книжном магазине, где путешественник во времени покупает её и отдаёт Шекспиру, а тот снимает копию и так далее… Кого в таком случае нужно считать автором бессмертной трагедии?

3.

Парадокс девочки и мальчика Мартин Гарднер / © www.post-gazette.com

В теории вероятностей этот парадокс также называют «Дети мистера Смита» или «Проблемы миссис Смит». Впервые он был сформулирован американским математиком Мартином Гарднером в одном из номеров журнала «Scientific American». Учёные спорят над парадоксом уже несколько десятилетий и существует несколько способов его разрешения. Поразмыслив над проблемой, вы можете предложить и свой собственный вариант.

В семье есть двое детей и точно известно, что один из них — мальчик. Какова вероятность того, что второй ребёнок тоже имеет мужской пол? На первый взгляд, ответ вполне очевиден — 50 на 50, либо он действительно мальчик, либо девочка, шансы должны быть равными. Проблема в том, что для двухдетных семей существует четыре возможных комбинации полов детей — две девочки, два мальчика, старший мальчик и младшая девочка и наоборот — девочка старшего возраста и мальчик младшего. Первую можно исключить, так как один из детей совершенно точно мальчик, но в таком случае остаются три возможных варианта, а не два и вероятность того, что второе чадо тоже мальчик — один шанс из трёх.

4. Парадокс Журдена с карточкой

Проблему, предложенную британским логиком и математиком Филиппом Журденом в начале XX-го века, можно считать одной из разновидностей знаменитого парадокса лжеца.

Филипп Журден

Представьте себе — вы держите в руках открытку, на которой написано: «Утверждение на обратной стороне открытки истинно». Перевернув открытку, вы обнаруживаете фразу «Утверждение на другой стороне ложно». Как вы понимаете, противоречие налицо: если первое утверждение правдиво, то второе тоже соответствует действительности, но в таком случае первое должно оказаться ложным. Если же первая сторона открытки лжива, то фразу на второй также нельзя считать истинной, а это значит, первое утверждение опять-таки становится правдой… Ещё более интересный вариант парадокса лжеца — в следующем пункте.

5. Софизм «Крокодил»

На берегу реки стоят мать с ребёнком, вдруг к ним подплывает крокодил и затаскивает ребёнка в воду. Безутешная мать просит вернуть её чадо, на что крокодил отвечает, что согласен отдать его целым и невредимым, если женщина правильно ответит на его вопрос: «Вернёт ли он её ребёнка?». Понятно, что у женщины два варианта ответа — да или нет. Если она утверждает, что крокодил отдаст ей ребёнка, то всё зависит от животного — посчитав ответ правдой, похититель отпустит ребёнка, если же он скажет, что мать ошиблась, то ребёнка ей не видать, согласно всем правилам договора.

© Коракс Сиракузский

Отрицательный ответ женщины всё значительно усложняет — если он оказывается верным, похититель должен выполнить условия сделки и отпустить дитя, но таким образом ответ матери не будет соответствовать действительности. Чтобы обеспечить лживость такого ответа, крокодилу нужно вернуть ребёнка матери, но это противоречит договору, ведь её ошибка должна оставить чадо у крокодила.

Стоит отметить, что сделка, предложенная крокодилом, содержит логическое противоречие, поэтому его обещание невыполнимо. Автором этого классического софизма считается оратор, мыслитель и политический деятель Коракс Сиракузский, живший в V-м веке до нашей эры.

6. Апория «Дихотомия»

© www. student31.ru

Ещё один парадокс от Зенона Элейского, демонстрирующий некорректность идеализированной математической модели движения. Проблему можно поставить так — скажем, вы задались целью пройти какую-нибудь улицу вашего города от начала и до конца. Для этого вам необходимо преодолеть первую её половину, затем половину оставшейся половины, далее половину следующего отрезка и так далее. Иначе говоря — вы проходите половину всего расстояния, затем четверть, одну восьмую, одну шестнадцатую — количество уменьшающихся отрезков пути стремится к бесконечности, так как любую оставшуюся часть можно разделить надвое, значит пройти весь путь целиком невозможно. Формулируя несколько надуманный на первый взгляд парадокс, Зенон хотел показать, что математические законы противоречат реальности, ведь на самом деле вы можете без труда пройти всё расстояние без остатка.

7. Апория «Летящая стрела»

Знаменитый парадокс Зенона Элейского затрагивает глубочайшие противоречия в представлениях учёных о природе движения и времени.

Апория сформулирована так: стрела, выпущенная из лука, остаётся неподвижной, так как в любой момент времени она покоится, не совершая перемещения. Если в каждый момент времени стрела покоится, значит она всегда находится в состоянии покоя и не движется вообще, так как нет момента времени, в который стрела перемещается в пространстве.

© www.academic.ru

Выдающиеся умы человечества веками пытаются разрешить парадокс летящей стрелы, однако с логической точки зрения он составлен абсолютно верно. Для его опровержения требуется объяснить, каким образом конечный временной отрезок может состоять из бесконечного числа моментов времени — доказать это не удалось даже Аристотелю, убедительно критиковавшему апорию Зенона. Аристотель справедливо указывал, что отрезок времени нельзя считать суммой неких неделимых изолированных моментов, однако многие учёные считают, что его подход не отличается глубиной и не опровергает наличие парадокса. Стоит отметить, что постановкой проблемы летящей стрелы Зенон стремился не опровергнуть возможность движения, как таковую, а выявить противоречия в идеалистических математических концепциях.

8. Парадокс Галилея

Галилео Галилей / © Wikimedia

В своём труде «Беседы и математические доказательства, касающиеся двух новых отраслей науки» Галилео Галилей предложил парадокс, демонстрирующий любопытные свойства бесконечных множеств. Учёный сформулировал два противоречащих друг другу суждения. Первое: есть числа, представляющие собой квадраты других целых чисел, например 1, 9, 16, 25, 36 и так далее. Существуют и другие числа, у которых нет этого свойства — 2, 3, 5, 6, 7, 8, 10 и тому подобные. Таким образом, общее количество точных квадратов и обычных чисел должно быть больше, чем количество только точных квадратов. Второе суждение: для каждого натурального числа найдётся его точный квадрат, а для каждого квадрата существует целый квадратный корень, то есть, количество квадратов равно количеству натуральных чисел.

На основании этого противоречия Галилей сделал вывод, что рассуждения о количестве элементов применены только к конечным множествам, хотя позже математики ввели понятие, мощности множества — с его помощью была доказана верность второго суждения Галилея и для бесконечных множеств.

9. Парадокс мешка картофеля

© nieidealne-danie.blogspot.com

Допустим, у некоего фермера имеется мешок картофеля весом ровно 100 кг. Изучив его содержимое, фермер обнаруживает, что мешок хранился в сырости — 99% его массы составляет вода и 1% остальные вещества, содержащиеся в картофеле. Он решает немного высушить картофель, чтобы содержание воды в нём снизилось до 98% и переносит мешок в сухое место. На следующий день оказывается, что, один литр (1 кг) воды действительно испарился, но вес мешка уменьшился со 100 до 50 кг, как такое может быть? Давайте посчитаем — 99% от 100 кг это 99 кг, значит соотношение массы сухого остатка и массы воды изначально было равно 1/99. После сушки вода насчитывает 98% от общей массы мешка, значит соотношение массы сухого остатка к массе воды теперь составляет 1/49. Так как масса остатка не изменилась, оставшаяся вода весит 49 кг.

Конечно, внимательный читатель сразу обнаружит грубейшую математическую ошибку в расчётах — мнимый шуточный «парадокс мешка картофеля» можно считать отличным примером того, как с помощью на первый взгляд «логичных» и «научно подкреплённых» рассуждений можно буквально на пустом месте выстроить теорию, противоречащую здравому смыслу.

10. Парадокс воронов

Карл Густав Гемпель / © Wikimedia

Проблема также известна, как парадокс Гемпеля — второе название она получила в честь немецкого математика Карла Густава Гемпеля, автора её классического варианта. Проблема формулируется довольно просто: каждый ворон имеет чёрный цвет. Из этого следует, что всё, что не чёрного цвета, не может быть вороном. Этот закон называется логическая контрапозиция, то есть если некая посылка «А» имеет следствие «Б», то отрицание «Б» равнозначно отрицанию «А». Если человек видит чёрного ворона, это укрепляет его уверенность, что все вороны имеют чёрный окрас, что вполне логично, однако в соответствии с контрапозицией и принципом индукции, закономерно утверждать, что наблюдение предметов не чёрного цвета (скажем, красных яблок) также доказывает, что все вороны окрашены в чёрный цвет. Иными словами — то, что человек живёт в Санкт-Петербурге доказывает, что он живёт не в Москве.

С точки зрения логики парадокс выглядит безукоризненно, однако он противоречит реальной жизни — красные яблоки никоим образом не могут подтверждать тот факт, что все вороны чёрного цвета.

4.12. Парадоксы-апории. Логика. Учебное пособие

4.12. Парадоксы-апории

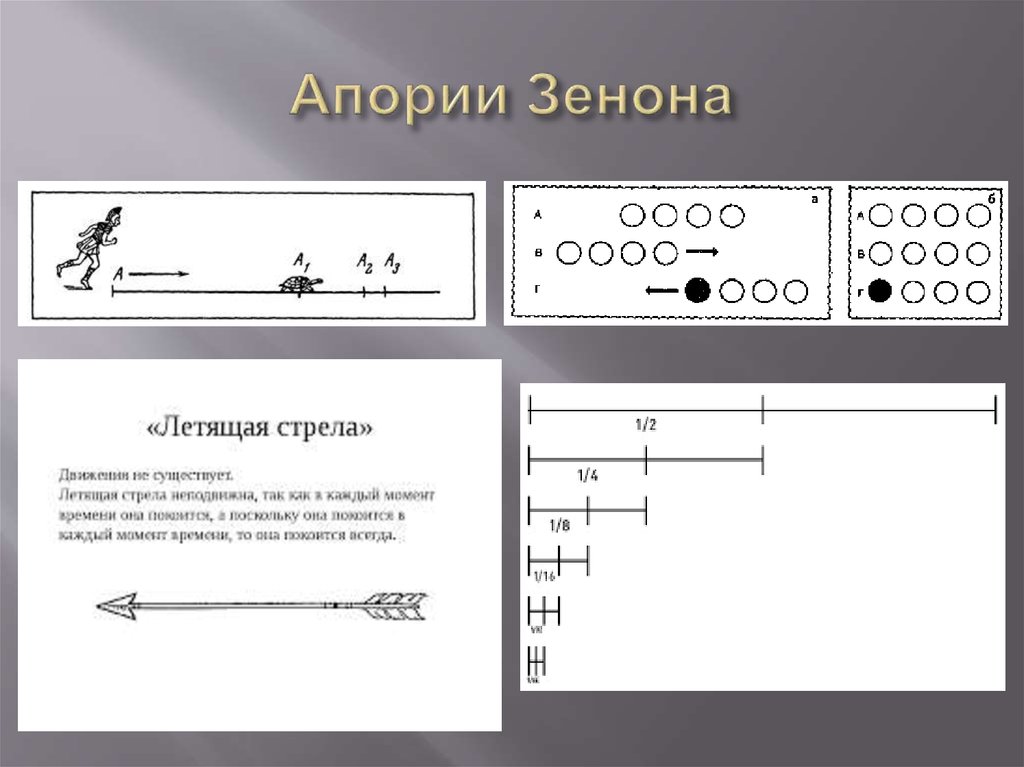
Отдельной группой парадоксов являются апории (греч. aporia – затруднение, недоумение) – рассуждения, которые показывают противоречия между тем, что мы воспринимаем органами чувств (видим, слышим, осязаем и т. п.) и тем, что можно мысленно проанализировать (проще говоря – противоречия между видимым и мыслимым). Наиболее известные апории выдвинул древнегреческий философ Зенон Элейский, который утверждал, что движение, наблюдаемое нами повсюду, невозможно сделать предметом мысленного анализа, т. е. движение можно видеть, но нельзя мыслить. Одна из его апорий называется «Дихотомия» (в пер. с греч. – деление пополам).

Допустим, некому телу надо пройти из пункта А в пункт В. Нет никакого сомнения в том, что мы можем увидеть, как тело, покинув один пункт, через какое-то время достигнет другого.

Однако давайте попробуем не доверять своим глазам, которые говорят нам о том, что тело движется, и попытаемся воспринять движение не глазами, а мыслью, постараемся не увидеть его, а помыслить. В этом случае у нас получится следующее. Прежде чем пройти весь свой путь из пункта А в пункт В, телу надо пройти половину этого пути, ведь если оно не пойдет половину пути, то, конечно же, не пройдет и весь путь. Но прежде чем тело пройдет половину пути, ему надо пройти 1/4 часть пути. Однако до того, как оно пройдет эту 1/4 часть пути, ему надо пройти 1/8 часть пути; а еще раньше ему требуется пройти 1/16 часть пути, а перед этим – 1/32 часть, а прежде того – 1/64 часть, а до этого – 1/128 часть и так до бесконечности. Значит, чтобы пройти из пункта А в пункт В, телу надо пройти бесконечное количество отрезков этого пути. Возможно ли пройти бесконечность? Невозможно! Следовательно, тело никогда не сможет пройти свой путь. Таким образом, глаза свидетельствуют, что путь будет пройден, а мысль, наоборот, отрицает это (видимое противоречит мыслимому).

Другая известная апория Зенона Элейского – «Ахиллес и черепаха» – говорит о том, что мы вполне можем увидеть, как быстроногий Ахиллес догоняет и перегоняет медленно ползущую впереди него черепаху; однако мысленный анализ приводит нас к необычному заключению, что Ахиллес никогда не сможет догнать черепаху, хотя он и движется в 10 раз быстрее нее. Когда он преодолеет расстояние до черепахи, то она за это же время (ведь она тоже движется) пройдет в 10 раз меньше (т. к. движется в 10 раз медленнее), а именно 1/10 часть того пути, который прошел Ахиллес, и на эту 1/10 часть будет впереди него. Когда Ахиллес пройдет эту 1/10 часть пути, то черепаха за это же время пройдет в 10 раз меньшее расстояние, т. е. 1/100 часть пути и на эту 1/100 часть будет впереди Ахиллеса. Когда он пройдет 1/100 часть пути, разделяющую его и черепаху, то она за это же время пройдет 1/1000 часть пути, все равно оставаясь впереди Ахиллеса, и так до бесконечности. Итак, мы вновь убеждаемся в том, что глаза говорят нам об одном, а мысль – о совершенно другом (видимое отрицается мыслимым).

Еще одна апория Зенона – «Стрела» – предлагает нам мысленно рассмотреть полет стрелы из одной точки пространства в другую. Наши глаза, конечно же, говорят о том, что стрела летит, или движется. Однако что будет, если мы попытаемся, отвлекаясь от зрительного впечатления, помыслить ее полет? Для этого, зададим себе простой вопрос: где сейчас находится летящая стрела? Если, отвечая на данный вопрос, мы скажем, что она в настоящий момент находится там-то, или где-то, то в этом случае у нас получится, что стрела не летит, а покоится, ведь находиться где-то, или быть в каком-то определенном месте, – это как раз и означает находиться в неподвижности, или покоиться. Таким образом, единственное, что мы можем ответить на вопрос о том, где сейчас находится летящая стрела, – это следующее: «Везде и нигде конкретно». Но разве возможно быть везде и нигде одновременно? Итак, при попытке помыслить полет стрелы мы натолклулись на логическое противоречие, на нелепость – стрела находится везде и нигде. Получается, что движение стрелы вполне можно увидеть, но его нельзя помыслить, вседствие чего оно невозможно, как и любое движение вообще. Иначе говоря, двигаться, с точки зрения мысли, а не чувственных восприятий, означает – быть в неком месте и не быть в нем одновременно, что, конечно же, невозможно.

В своих апориях Зенон столкнул на «очной ставке» данные органов чувств (говорящие о множественности, делимости и движении всего существующего, уверяющие нас, что быстроногий Ахиллес догонит медлительную черепаху, а стрела долетит до цели) и умозрение (которое не может помыслить движение или множественность объектов мира, не впадая при этом в противоречие).

Однажды, когда Зенон доказывал при стечении народа немыслимость и невозможность движения, среди его слушателей оказался не менее известный в Древней Греции философ Диоген Синопский. Ничего не говоря, он встал и начал расхаживать, полагая, что этим он лучше всяких слов доказывает реальность движения. Однако Зенон не растерялся и ответил:

«Ты не ходи и руками-то не маши, а попробуй разумом разрешить сию сложную проблему». По поводу этой ситуации есть даже следующее стихотворение А. С. Пушкина:

Движенья нет, сказал мудрец брадатый,

Другой смолчал и стал пред ним ходить.

Сильнее бы не мог он возразить;

Хвалили все ответ замысловатый.

Но, господа, забавный случай сей

Другой пример на память мне приводит:

Ведь каждый день пред нами Солнце ходит,

Однако ж прав упрямый Галилей.

И действительно, видим же мы совершенно отчетливо, что Солнце движется по небу каждый день с Востока на Запад, а на самом-то деле оно неподвижно (по отношению к Земле). Так почему бы нам не предположить, что и другие объекты, которые мы видим движущимися, на самом деле могут быть неподвижными, и не спешить с утверждением о том, что элейский мыслитель был неправ?

Данный текст является ознакомительным фрагментом.

Апории Зенона

Апории Зенона Элеаты — авторы первых логических задач и мысленных экспериментов. Они во многом предвосхитили платоновские упражнения в диалектике и аристотелевские упражнения в логике.Зенон из Элеи известен своими апориями (в переводе апория — затруднение, трудность)

4.10. Парадоксы-антиномии

4.10. Парадоксы-антиномии От софизмов следует отличать логические парадоксы (греч. paradoxos – неожиданный, странный). Парадокс в широком смысле слова – это нечто необычное и удивительное, то, что расходится с привычными ожиданиями, здравым смыслом и жизненным опытом.

3. Проблема бесконечности и своеобразие античной диалектики. Апории Зенона

3. Проблема бесконечности и своеобразие античной диалектики. Апории Зенона Зенон выдвинул ряд парадоксальных положений, которые получили название апорий («апория» в переводе с греческого означает «затруднение», «безвыходное положение»). С их помощью он хотел доказать,

Парадоксы времени

Парадоксы времени Предыдущая глава фактически была посвящена проблеме существования мира в пространстве, теперь же обратим внимание на его существование во времени. Что это вообще такое — время? Очевидный ответ: количественная характеристика потока происходящих

Парадоксы морали

Парадоксы морали Автономная мораль с ее претензией на абсолютность неизбежно оборачивается парадоксальностью. Обладая изначальностью по отношению к сознательной (целесообразной) человеческой деятельности и будучи тем самым, ее пределом, мораль не может обнаружиться

ПАРАДОКСЫ

ПАРАДОКСЫ «…Истина все же скорее возникает из ошибки, чем из спутанности…» Ф. Бэкон «Логические парадоксы озадачили с момента своего открытия и, вероятно, будут озадачивать нас всегда. Мы должны, я думаю, рассматривать их не столько как проблемы, ожидающие решения,

ПАРАДОКСЫ И ХИТРЕЦЫ

ПАРАДОКСЫ И ХИТРЕЦЫ В Древней Греции пользовался большой популярностью рассказ о крокодиле и матери. Крокодил выхватил у женщины, стоявшей на берегу реки, ее ребенка. На ее мольбу вернуть ребенка крокодил, пролив, как всегда, крокодилову слезу, ответил: — Твое несчастье

3. Своеобразие античной диалектики.

Апории Зенона

3. Своеобразие античной диалектики. Апории Зенона Зенон выдвинул ряд парадоксальных положений, которые получили название апорий (апория в переводе с греческого означает «затруднение», «безвыходное положение»). С их помощью он хотел доказать, что бытие едино и неподвижно,

Парадоксы сознания[33]

Парадоксы сознания[33] Можно допустить, что все люди обладают сознанием, но это вовсе не означает, что все они отдают себе в этом отчет. Вся эта сфера не предполагает полной однородности. Мы не знаем, как рождается и возникает сознание, мы также не знаем, каковы его связи с

ПАРАДОКСЫ ДЕМОКРАТИИ

ПАРАДОКСЫ ДЕМОКРАТИИ Американский образец демократии, сформировавшийся в XVIII–XIX веках, фактически представлял демократию меньшинства, типичным носителем которой выступал белый, протестант, домовладелец. Так называемое политическое участие — претензия быть

Парадоксы – пища для ума

Парадоксы – пища для ума Онтологически любой объект является конечной реализацией абстрактных систем (параструктур). Параструктуры являются реализациями фрагментов иерархий подобия. Но не существует единой вселенской иерархии, «всемирная пирамида» невозможна.

Истины и парадоксы

Истины и парадоксы Научно-техническая революция поставила ряд сложных философских и психологических вопросов, живо волнующих умы в сегодняшнем мире. Несмотря на ошеломляющую новизну, которую вносит в нашу жизнь бурное развитие науки и техники, многие из этих вопросов

ПАРАДОКСЫ НЕТОЧНОСТИ

ПАРАДОКСЫ НЕТОЧНОСТИ Говорят, главное во всяком деле — уловить момент. Это относится, пожалуй, и к таким делам, как размышление и рассуждение. Однако здесь «момент» улавливается особенно трудно, и существенную роль в этом играют как раз неточные понятия.— Один мальчик

АПОРИИ ЗЕНОНА

АПОРИИ ЗЕНОНА Обратимся теперь к конкретным софизмам и тем проблемам, которые стоят за ними.Знаменитые рассуждения древнегреческого философа Зенона «Ахиллес и черепаха», «дихотомия» и др., называемые обычно «апориями» («затруднениями»), были направлены будто бы против

Определение и примеры апории

Определение апории

Апория — это фигура речи, в которой говорящий выражает или выражает сомнение или недоумение в отношении вопроса (часто притворно) и спрашивает аудиторию, как ему следует действовать. Сомнения могут появляться в виде риторических вопросов, часто в начале текста.

Апория — это логический парадокс, в котором говорящий сеет семена сомнения по поводу предмета. Эта риторическая стратегия может вызвать у аудитории симпатию к говорящему в отношении дилеммы, перед которой он стоит.0005

Особенности апории

• Апория используется как риторический прием в литературе.
• Его также называют «сомнением», что означает, что неуверенность всегда ложна.
• Это может быть вопрос или утверждение.
• Часто используется в философии. Это относится к философским вопросам и темам, на которые нет очевидных ответов.
• Платон и Сократ были известны тем, что использовали апорию.

Примеры апорий в литературе

Пример №1:

Гамлет (Уильям Шекспир)

«Быть ​​или не быть: вот в чем вопрос.
Что благородней духом терпеть
Пращи и стрелы безудержной судьбы,
Иль с оружием в руках против моря бед,
И противоборством покончить с ними? Умереть: спать;
Чем летать к другим, которых мы не знаем?
Таким образом, совесть делает всех нас трусами…»

Это яркий пример апории, доступный в английской литературе. Это вступительный монолог, произнесенный Гамлетом в знаменитой пьесе. Здесь утверждение «Быть ​​или не быть» вносит неопределенность, характеризующую абзац.

Пример #2:

Безымянный (Сэмюэл Беккет)

«Где теперь? Кто сейчас? Когда сейчас? Беспрекословный. Я, говорю я. Неверующий. Вопросы, гипотезы, назовите их так. Продолжайте, продолжайте, называйте это продолжением, называйте это».

«…или утверждениями и отрицаниями, аннулируемыми по мере произнесения, или рано или поздно?»

«…Должны быть другие смены. Иначе было бы совсем безнадежно. Прежде чем идти дальше, я должен упомянуть…»

«Может ли быть афетичен иначе, чем по незнанию? Я не знаю.»

«Что мне делать, что мне делать, что мне делать в моей ситуации, как поступить? Чистой и простой апорией…»

«Это буду я? Это будет тишина, где я, я не знаю, я никогда не узнаю, в тишине, которую ты не знаешь, ты должен продолжать, я не могу продолжать, я буду продолжать».

Вся работа Беккета характеризуется использованием апории. В этих отрывках много вопросов и сомнений, и отсрочка смысла. Для Беккета апория никогда не может рассматриваться как неизменное состояние незнания.

Пример №3:

American Buffalo (от Дэвида Мамета)

Дон :        «У нас есть сделка с этим человеком».
Научите :    «С Флетчером».
Дон        «Да. ”
Научите :    “У нас была сделка с Бобби”.
Дон :        «Что это значит?»
Научите :    «Ничего».
Дон :        «Это не так?»
Научить :    «Нет.
Дон :        «Что вы имели в виду?»
Научите :    «Я ничего не имел в виду».
Дон        «Вы этого не сделали».
Научить :    «Нет?»

Вышеприведенный отрывок является примером апории, иллюстрирующей большое количество сомнений в речи. Есть и неуверенность, и должное вопрошание, но выраженное более светлым тоном.

Пример #4:

Неизбранная дорога (Роберт Фрост)

«Две дороги расходятся в желтом лесу,
И извините, я не смог пройти обе
И будь один путник, долго я стоял
И смотрел вниз, насколько мог
Туда, где он изгибался в подлеске;
Две дороги расходились в лесу, и я…
Я выбрал менее проторенную,
И в этом вся разница.

В последних двух строках данного стихотворения поэт использует апорию, которая представляет собой внутренне противоречивый тупик, неразрешимый в тексте. Точно так же и в поэме читатели оказываются в тупике, а окончательные доказательства впадают в парадокс.

Функция апории

Апория — это выражение сомнения или неуверенности. Когда неуверенность и сомнения являются подлинными, это может указывать на реальный тупик и стимулировать аудиторию к рассмотрению различных вариантов выхода из ситуации. Это может показать смирение говорящего, если сомнение, которое он выражает, искренне. Тем не менее, он предназначен для того, чтобы дать аудитории указания относительно того, что говорящий хочет сказать, если сомнения неискренни.

Апория вызывает неуверенность и заставляет аудиторию обнаружить уверенность через последующие утверждения говорящего. Основная цель – предоставить зрителям возможность проанализировать и оценить ситуацию.

сообщите об этом объявлении

Риторический прием, в котором кто-то выражает сомнение

Этот пост является частью серии статей о риторике и риторических приемах. Для просмотра других сообщений из этой серии перейдите по этой ссылке. Подробный пошаговый обзор того, как написать план выступления, см. в этом посте.

Устройство : Апория

Происхождение : От греческого ἄπορος (апорос), что означает «непроходимый».

На простом английском языке: Выражение неуверенности или сомнения.

Эффект:

• • Когда сомнение или неуверенность являются подлинными, это может сигнализировать о реальной дилемме и побуждать аудиторию думать о различных вариантах решения.
• • В случае искренних сомнений может показать смирение говорящего.
• • Когда сомнение симулируется, оно часто используется для того, чтобы подвести аудиторию к тому, что хочет сказать оратор.

Примечания:

• • Апория также известна как dubitatio , хотя некоторые утверждают, что в dubitatio неопределенность всегда притворна или неискренна.
• • Апория может быть как утверждением, так и вопросом.
• • Распространенный пример притворной апории  можно увидеть, когда кто-то должен произнести речь об очень близком друге или родственнике; например, на свадьбе или в гостях. В таких речах мы часто слышим фразы типа: «Что я могу сказать о таком-то и таком-то?» Нет никаких сомнений в том, что спикеру есть что сказать.
• • Апория также является философским термином. Это относится к философским вопросам, на которые нет четких ответов. Сократ и Платон были известны такими вопросами.
    

Примеры:

«Я не потеряю информацию о вас и вашей семье; , но я не знаю, с чего начать. Рассказать, как твой отец Тромес был рабом в доме Эльпиаса, который держал начальную школу возле храма Тесея, и как он носил кандалы на ногах и деревянный ошейник на шее? Или как твоя мать устраивала свадьбы при дневном свете во флигеле по соседству с костоправом Геросом и так воспитала тебя, чтобы играть в живых картинах и преуспевать в второстепенных ролях на сцене?

—  Демосфен, На короне , 330 г. до н.э.

———

«Забрал ли он их у своих товарищей более нагло, отдал их блуднице более похотливо, отнял их у римского народа более нечестиво или изменил их более самонадеянно, я не могу точно сказать .

— Цицерон

———

«Мы, демократы, считаем, что страна работает лучше с сильным средним классом, с реальными возможностями для бедняков пробиться в него, с неустанной ориентацией на будущее, с бизнесом. и правительство действительно работает вместе, чтобы способствовать росту и всеобщему процветанию. Видите ли, мы считаем, что философия «Мы все вместе» гораздо лучше, чем «Ты сам по себе».   Так кто же прав? Что ж, с 1961 года, в течение 52 лет, республиканцы находились в Белом доме 28 лет, демократы — 24. За эти 52 года наша частная экономика создала 66 миллионов рабочих мест в частном секторе. Итак, какова оценка работы? Республиканцы: 24 миллиона. Демократы: 42 [миллиона]».
…
«Республиканцы называют это Obamacare и говорят, что это государственное поглощение здравоохранения, которое они отменят. Они правы? Давайте посмотрим, что произошло до сих пор».

— Билл Клинтон, Национальный съезд Демократической партии, 5 сентября 2012 г.