Апория Зенона «Стадион»: физическая дискретность и математическая непрерывность | Философские байки
Гоплитодром — бег со щитом. Добавлен в Олимпийские состязания на 65-й Олимпиаде в 520 до н. э. Чернофигурная вазописьГоплитодром — бег со щитом. Добавлен в Олимпийские состязания на 65-й Олимпиаде в 520 до н. э. Чернофигурная вазопись
Одна из оригинальных апорий Зенона, посвященных движению, называется Стадий, Стадион или Ристалище.
Формулировка задачи
На стадионе находится три группы спортсменов. Первая группа (А) не двигается, вторая (В) двигается вправо, а третья (Г) — влево. Вторая группа и третья движутся хоть и в разных направлениях, но с одинаковой скоростью.
Пусть спортсмены внутри каждой группы станут максимально плотно, так, чтобы между ними остался один-единственный неделимый квант пространства.
Какое расстояние спортсмены из группы Б пройдут за один неделимый квант времени? Зенон говорит, что за один квант времени спортсмены пройдут неделимый квант пространства. Ведь меньше они пройти не могут, да и больше тоже: если они пройдут два кванта пространства, то каждый квант пространства они пройдут за 1/2 кванта времени.
Ведь меньше они пройти не могут, да и больше тоже: если они пройдут два кванта пространства, то каждый квант пространства они пройдут за 1/2 кванта времени.
Но спортсмены из группы Г тоже идут с такой же скоростью. Поэтому за этот же квант времени спортсмены из группы В сдвинутся относительно спортсменов из группы Г на два кванта пространства. Таким образом, один квант пространства окажется пройденным за 1/2 кванта времени.
Получается, что неделимый квант времени всё же окажется делимым.
изображение с просторов интернетаизображение с просторов интернета
В чём подвох?
Подвох, как обычно, в самих посылках апории.
В этой апории Зенон берёт три утверждения за основу:
1. существует неделимый квант времени;
2. существует неделимый квант пространства;
3. Любой отрезок можно представить как сумму его частей.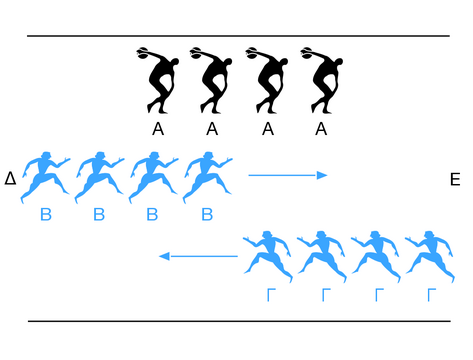
В общем-то, если отринуть любое из этих утверждений (чего и добивался Зенон), апории не получится.
А вот что пишет Джеральд Уитроу (Gerald James Whitrow) в книге «Естественная философия времени» по поводу этой апории:
Джеральд УитроуДжеральд Уитроу
«…даже Зенон при обсуждении апории «Стадий» молчаливо обращался к представлению о непрерывности, хотя данная апория основана на предположении об атомарном характере пространства и времени. Логически непротиворечивое решение этой проблемы должно опираться на представление о последовательных дискретных состояниях, между которыми нельзя вставить никакие другие состояния… »
Иными словами, если квант времени по условиям задачи неделим, то и дробить его на части нельзя.
« Поэтому понятия физической дискретности и математической непрерывности, когда обсуждаются все тонкости, связанные с проблемами, поставленными Зеноном, следует строго различать».
|
Проблема – как, в конечном счете, устроены геометрические объекты, из чего они «состоят» – была важной проблемой для греческой философии. Эта проблема привлекла внимание и Зенона – представителя Элейской философской школы. Элейская школа выступала с парадоксальным учением, что существует только единое и неподвижное и неизменное бытие, повсюду одинаковое: хотя людям кажется, что бытие множественно и подвержено переменам, это мнение ведет к противоречиям и поэтому должно быть отброшено. Наиболее известными и важными для математики стали сформулированные Зеноном четыре апории (т. е. парадокса), направленных против существования движения. По-видимому, первые две апории Зенона подразумевали, что пространство и время делимы до бесконечности, а другие две основывались на противоположном представлении, будто пространственная протяженность и временная длительность состоят из неделимых моментов. Зенон пытался показать, что каждое из двух противоположных воззрений в результате ведет к противоречию, а значит, должна быть отвергнута сама идея движения, которое представляет собой лишь иллюзию.
Хотя большинство философов не могли принять странные выводы Зенона о несуществовании движения, поставленные Зеноном проблемы заставили более пристально вглядываться в понятия, связанные с пространством и временем. Кроме того, апории Зенона связаны и с рядом других вопросов, касающихся математики (суммирование бесконечного числа слагаемых, относительность движения, соотношение математической теории и физической реальности и т. д.). Интересно, а Вы что думаете об этих апориях? |
Ответы на вопрос «4.Апории Зенона»
Задачу отстоять воззрения Парменида против выдвинутых возражений взял на себя ученик и друг Парменида Зенон.
Зенон развил ряд аргументов в защиту учения Парменида. Метод, применённый им в этих аргументах, впоследствии дал основание Аристотелю называть Зенона родоначальником “диалектики”. Под “диалектикой” Аристотель в этом случае понимает искусство выяснения истины путём обнаружения внутренних противоречй, заключающихся в мыслях противника, и путём устранения этих противоречий.
Метод Зенона сходен с тем, который называется в математике <доказательством от противного>. Зенон принимает — условно — тезисы противников Парменида. Он принимает, (1) что пространство может быть мыслимо как пустота, как отдельное от наполняющего пространство вещества; (2) что мыслимо существование множества вещей; (3) что может быть мыслимо движение. Приняв условно эти три предположения, Зенон доказывает, будто признание их ведет с необходимостью к противоречиям. Тем самым доказывается, что предположения эти ложны. Но если они ложны, то необходимо должны быть истинны противоречащие им утверждения. А это и есть утверждения Парменида. Стало быть, утверждения Парменида истинны: пустота, множество и движение немыслимы. Ни Парменид, ни Зенон не отрицают реальности пустоты, множества, движения для наших чувств. Они отрицают лишь возможность мыслить пустоту, мыслить множество и мыслить движение, не впадая при этом в противоречия.
Он принимает, (1) что пространство может быть мыслимо как пустота, как отдельное от наполняющего пространство вещества; (2) что мыслимо существование множества вещей; (3) что может быть мыслимо движение. Приняв условно эти три предположения, Зенон доказывает, будто признание их ведет с необходимостью к противоречиям. Тем самым доказывается, что предположения эти ложны. Но если они ложны, то необходимо должны быть истинны противоречащие им утверждения. А это и есть утверждения Парменида. Стало быть, утверждения Парменида истинны: пустота, множество и движение немыслимы. Ни Парменид, ни Зенон не отрицают реальности пустоты, множества, движения для наших чувств. Они отрицают лишь возможность мыслить пустоту, мыслить множество и мыслить движение, не впадая при этом в противоречия.
Рассмотрим аргументы Зенона в отдельности по этим трем вопросам. Начнем с вопроса о мыслимости пустоты, т. е. пространства, отделенного от вещества. Если мы допустим существование такого пространства, то вступает в силу следующее рассуждение. Все существующее находится где-нибудь в пространстве. Но чтобы существовать, пространство тоже должно находиться <где-нибудь>, т. е. существовать во втором пространстве. Это второе пространство в свою очередь должно существовать в третьем пространстве, и так до бесконечности. Но это абсурдно. Следовательно, пространство как отдельное от вещества немыслимо.
Все существующее находится где-нибудь в пространстве. Но чтобы существовать, пространство тоже должно находиться <где-нибудь>, т. е. существовать во втором пространстве. Это второе пространство в свою очередь должно существовать в третьем пространстве, и так до бесконечности. Но это абсурдно. Следовательно, пространство как отдельное от вещества немыслимо.
Второй вопрос-о мыслимости множества. Допустим, что множество мыслимо. Тогда возникают вопросы: 1. Каким необходимо мыслить каждый в отдельности элемент этого множества?
2. Каким необходимо мыслить общее количество элементов множества: будет ли их сумма числом конечным или бесконечным?
Исследование Зенона показывает, что по обоим этим вопросам получаются противоречивые ответы. По первому вопросу — каким должен мыслиться каждый отдельный элемент множества — оказывается, что о каждом таком элементе необходимо придется отвечать, что он одновременно и не имеет никакой величины и бесконечно велик по величине.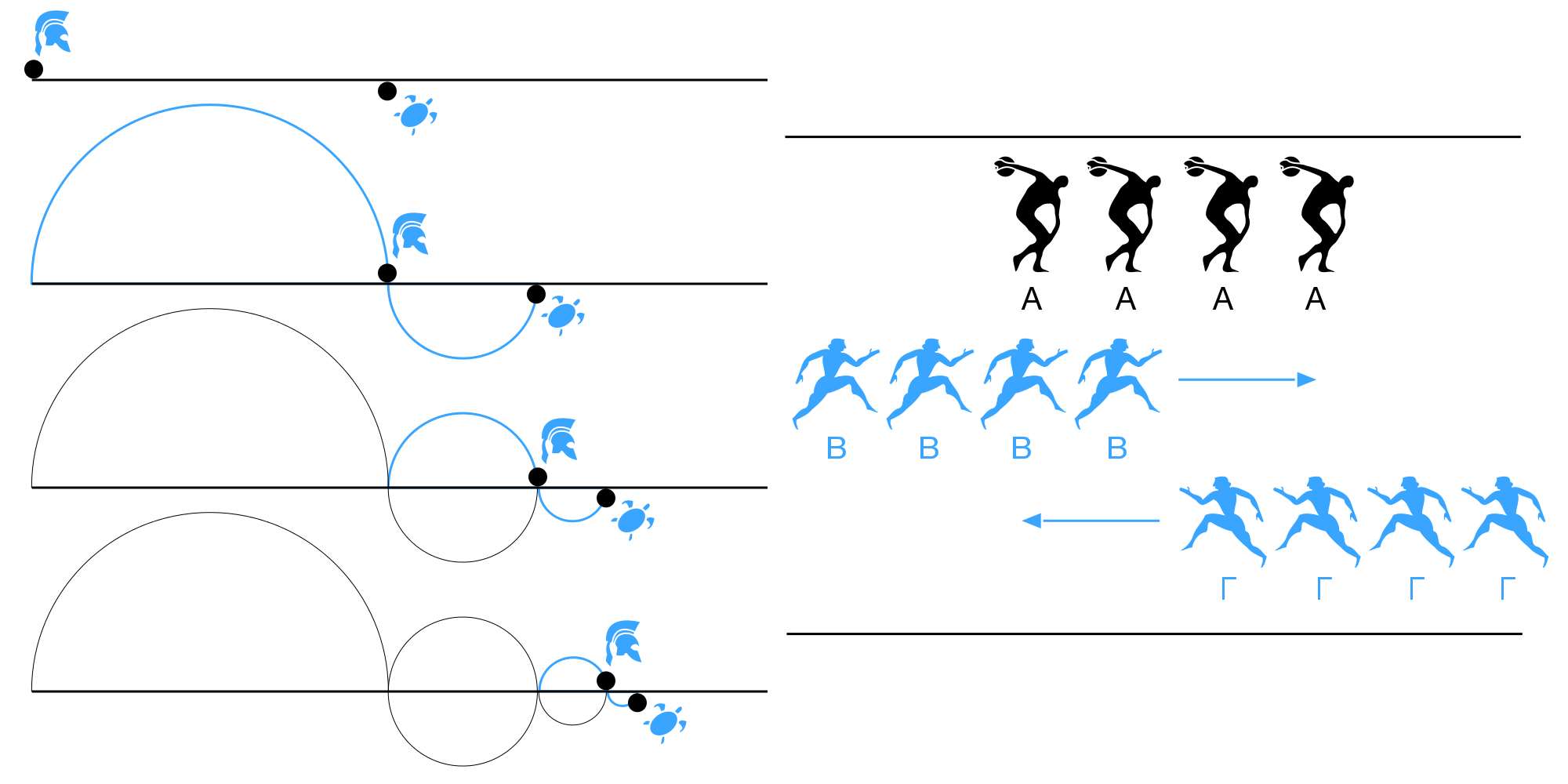 По второму вопросу — какой должна мыслиться сумма элементов множества — оказывается, что она должна мыслиться и как число конечное, и как число бесконечное.
По второму вопросу — какой должна мыслиться сумма элементов множества — оказывается, что она должна мыслиться и как число конечное, и как число бесконечное.
Исследование по третьему вопросу — о мыслимости движения, так же необходимо приводит к противоречащим утверждениям.
Аргументы Зенона по этому вопросу приобрели широкую известность. Зенон разработал несколько таких аргументов, из которых до нас дошли четыре: <Дихотомия (деление на два)>, <Ахилл>, <Летящая стрела> и <Стадий>
Общая их схема -то же опровержение <от противного>. Допустим, вместе с противниками Парменида будто движение мыслимо. Тогда о движущемся теле или о движущихся телах необходимо придется высказывать противоречащие друг другу утверждения:
1 ) что движение возможно и 2) что оно невозможно. При помощи четырех аргументов Зенон доказывает, что движение невозможно.
Оно невозможно, во-первых, как движение одного-единственного тела, переходящего по прямой из одной ее точки в другую. Чтобы пройти некоторую дистанцию, отделяющую точку А от точки B, тело должно предварительно пройти половину этой дистанции; чтобы пройти половину, оно должно предварительно пройти половину этой половины, и т.д. до бесконечности. В результате этого тело не только не может пройти из точки А в точку B, но не может даже покинуть точку А, т. е. движение от точки А к точке B не может не только завершиться, однажды начавшись, но даже не может начаться. Таков смысл аргумента <Дихотомия>.
Чтобы пройти некоторую дистанцию, отделяющую точку А от точки B, тело должно предварительно пройти половину этой дистанции; чтобы пройти половину, оно должно предварительно пройти половину этой половины, и т.д. до бесконечности. В результате этого тело не только не может пройти из точки А в точку B, но не может даже покинуть точку А, т. е. движение от точки А к точке B не может не только завершиться, однажды начавшись, но даже не может начаться. Таков смысл аргумента <Дихотомия>.
Немыслимость движения одного, отдельно взятого тела доказывается также посредством аргумента <Летящая стрела>. По предположению, стрела летит, т. е. движется в пространстве. Но о ней в то же время необходимо утверждать, что она в каждое мгновение полета занимает пространство, равное собственной длине, т. е. пребывает в пределах этой части пространства, <значит> в нем неподвижна. Выходит, стало быть, что летящая стрела и движется, и не движется.
Но движение немыслимо и как движение двух тел друг относительно друга. Оно немыслимо, во-первых, как движение по прямой двух тел, разделенных некоторой дистанцией и одновременно движущихся в одном и том же направлении, причем тело, движущееся позади, движется быстрее того, что движется впереди. Зенон доказывает, что при этих условиях тело, движущееся с большей скоростью, никогда не догонит того, что уходит от него с меньшей скоростью. Ахилл, славившийся быстротой своего бега, никогда не догонит убегающей от него черепахи. Пусть Ахилл бежит быстрее черепахи, но по истечении любого промежутка времени, как бы мал он ни был, черепаха успеет пройти расстояние, которое, как бы незначительно оно ни было, никогда не будет равно нулю. Следовательно, рассуждает Зенон, ни в один момент бега вся дистанция, отделяющая Ахилла от черепахи, не превратится в нуль, и потому Ахилл действительно никогда не догонит черепаху. Тот же результат получается, если применить к случаю Ахилла аргумент <Дихотомия>. В начальный момент бега Ахилла отделяет от черепахи расстояние AB.
Оно немыслимо, во-первых, как движение по прямой двух тел, разделенных некоторой дистанцией и одновременно движущихся в одном и том же направлении, причем тело, движущееся позади, движется быстрее того, что движется впереди. Зенон доказывает, что при этих условиях тело, движущееся с большей скоростью, никогда не догонит того, что уходит от него с меньшей скоростью. Ахилл, славившийся быстротой своего бега, никогда не догонит убегающей от него черепахи. Пусть Ахилл бежит быстрее черепахи, но по истечении любого промежутка времени, как бы мал он ни был, черепаха успеет пройти расстояние, которое, как бы незначительно оно ни было, никогда не будет равно нулю. Следовательно, рассуждает Зенон, ни в один момент бега вся дистанция, отделяющая Ахилла от черепахи, не превратится в нуль, и потому Ахилл действительно никогда не догонит черепаху. Тот же результат получается, если применить к случаю Ахилла аргумент <Дихотомия>. В начальный момент бега Ахилла отделяет от черепахи расстояние AB. Ахилл догонит черепаху в тот момент, когда это расстояние, уменьшаясь, обратится в нуль. Но чтобы это произошло, расстояние AB должно предварительно уменьшиться до половины. В свою очередь, чтобы уменьшиться до половины, оно должно предварительно уменьшиться до половины этой половины, и т. д. до бесконечности. Итог тот же, что и в <Дихотомии>: дистанция AB никогда не обратится в нуль.
Ахилл догонит черепаху в тот момент, когда это расстояние, уменьшаясь, обратится в нуль. Но чтобы это произошло, расстояние AB должно предварительно уменьшиться до половины. В свою очередь, чтобы уменьшиться до половины, оно должно предварительно уменьшиться до половины этой половины, и т. д. до бесконечности. Итог тот же, что и в <Дихотомии>: дистанция AB никогда не обратится в нуль.
§ 9. Смысл аргументов Зенона. Антология реалистической феноменологии
§ 9. Смысл аргументов Зенона
Анализ возражений Зенона против движения и основополагающих попыток опровержения его аргументов привел нас к примечательному результату, который мы предвидели в самом начале: возникающие трудности относятся не к движению как таковому, а связаны с ним лишь постольку, поскольку оно происходит в пространстве и времени. Только эти две существенные непрерывные формы служат основой парадоксов Зенона. Еще шаг вперед – и мы сможем также исключить время и иметь в виду только пространство, пространственные расстояния, пути и их взаимоотношения. И мы можем позволить себе даже совершенно радикальный способ рассмотрения, абстрагироваться также от самого пространства и сохранить в качестве объекта исследования только непрерывное количество или вообще просто континуум. Каковы, собственно, основные доводы, в которых заключается суть аргументов Зенона?
И мы можем позволить себе даже совершенно радикальный способ рассмотрения, абстрагироваться также от самого пространства и сохранить в качестве объекта исследования только непрерывное количество или вообще просто континуум. Каковы, собственно, основные доводы, в которых заключается суть аргументов Зенона?
1. Расстояние, путь, не пройденный путь, а путь, который следует пройти – до какого-либо измерения и какого-либо движения, делим до бесконечности; он содержит актуальную бесконечность точек. Причем совершенно не имеет значения, «составляем» ли мы прямую из бесконечного количества точек или, напротив, рассматриваем ее в качестве первичного единства данности, и ограничиваемся тем, что выделяем в ней точки как вторичные элементы. В обоих случаях мы имеем дело с актуальной бесконечностью. Нам не нужны движение и движущееся: геометрическая прямая с ее актуальной бесконечностью точек уже противостоит для нас всем затруднениям дихотомии.
2. Существует принципиальная возможность установить определенную и взаимную корреляцию между всеми точками пути обоих объектов движения или, обобщеннее, между всеми точками двух отрезков линий различной длины. Очевидно, здесь мы в столь же малой степени, как и в первом случае, имеем дело с движением или с движущимся, но имеем дело единственно с отношениями между геометрическими единствами, между математическими величинами. Следовательно, парадоксы отнюдь не имеют только форономическое значение и форономическую ценность. Они находят значительно более широкое применение – мы могли бы сказать, что они, по сути, содержатся в каждой геометрической, алгебраической и арифметической формуле. Чтобы убедиться в этом, проще всего перевести парадоксы Зенона на математический язык и привести при этом несколько элементарных примеров:[346]
Очевидно, здесь мы в столь же малой степени, как и в первом случае, имеем дело с движением или с движущимся, но имеем дело единственно с отношениями между геометрическими единствами, между математическими величинами. Следовательно, парадоксы отнюдь не имеют только форономическое значение и форономическую ценность. Они находят значительно более широкое применение – мы могли бы сказать, что они, по сути, содержатся в каждой геометрической, алгебраической и арифметической формуле. Чтобы убедиться в этом, проще всего перевести парадоксы Зенона на математический язык и привести при этом несколько элементарных примеров:[346]
а) Дихотомия. Возьмем переменную Х на отрезке от О до А; тогда аргумент «дихотомия» состоит в указании, что переменная должна проходить в определенной последовательности все величины от О до А.
в) Ахиллес. Две переменные связаны отношением Y = A X. Каждой величине X соответствует одна и только одна величина Y, и наоборот. Несмотря на это, Y возрастает быстрее, чем X, пока, наконец, не становится Y = X + C.
c) Стрела. Переведенный на математический язык аргумент «стрела» означает следующее: все величины одной переменной являются постоянными.
d) Стадий. Этот аргумент еще раз показывает нам, что можно установить однозначное и взаимное соотношение между всеми точками двух или нескольких отрезков линий – невзирая на их данную величину; этот факт выражен формулой Y = A X.
Добавим сюда еще несколько простых примеров, которые позволят нам еще лучше понять смысл парадоксов Зенона, как абстрактных формул, освобожденных от форономических облачений. Мы хотим представить в рамках декартовых координат простейшую мыслимую формулу: Y = X.
Линия, заданная этой формулой, есть, очевидно, прямая. Каждая точка этой прямой с необходимостью имеет соответствующую точку на линии абсцисс, и наоборот: ни одна точка не может отсутствовать, а также ни одна не может соответствовать нескольким. Несмотря на это, O Xn < O Xn Yn. Другой пример, который можно рассматривать как геометрическое представление как «Ахиллеса», так и «стадия»: возьмем две параллельные прямые А и В; если угодно, даже равной величины. Пересечем теперь эти прямые перпендикуляром С, которому мы позволим вращаться относительно лежащей не на параллельных прямых точки О. Очевидно, что каждому положению точки О соответствуют две точки на прямых А и В и что, следовательно, все точки на прямой А находятся в однозначной и взаимной корреляции с точками прямой В – это притом, что соответствующий отрезок на прямой В равен лишь части отрезка на прямой А.
Пересечем теперь эти прямые перпендикуляром С, которому мы позволим вращаться относительно лежащей не на параллельных прямых точки О. Очевидно, что каждому положению точки О соответствуют две точки на прямых А и В и что, следовательно, все точки на прямой А находятся в однозначной и взаимной корреляции с точками прямой В – это притом, что соответствующий отрезок на прямой В равен лишь части отрезка на прямой А.
На это нам невозможно возразить, что вращением прямой С мы снова ввели движение; ведь вращающаяся прямая представляет не что иное, как пучок лучей, который исходит из точки О.
Возьмем какую-нибудь кривую линию, например, окружность. Как известно, в каждой точке окружности можно провести касательную, причем можно провести столько касательных, чтобы окружности не была «искривлена» ни в одной точке самой себя. Стало быть, где она тогда искривляется? Совершенно очевидно, что мы снова сталкиваемся с неискоренимой проблемой стрелы – а именно: «где» движется движущееся и как оно вообще движется, когда оно не движется ни в одной точке своего пути? Здесь в случае с окружностью, так же, как и в аргументе Зенона, можно найти выход из положения в отношении данной точки с непосредственно соседней или непосредственно следующей за ней в столь же малой мере (как это сделал Эвеллин), а именно попросту потому, что такой непосредственно соседней или следующей точки вообще нет. Тотчас же перед нами встает проблема «дихотомии», так как кажется невозможным перейти от начального положения к непосредственно следующему, поскольку такого следующего вообще не существует. Итак, как возможно движение?
Тотчас же перед нами встает проблема «дихотомии», так как кажется невозможным перейти от начального положения к непосредственно следующему, поскольку такого следующего вообще не существует. Итак, как возможно движение?
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесПрограммная платформа zenon для автоматизации инфраструктуры, производственных процессов, инженерных систем и механизмов
Gorenjske Elektrarne — дочернее предприятие одной из ведущих энергетических компаний Словении Elektro Gorenjska, специализирующейся на развитии энергетики из возобновляемых источников, в том числе солнечной и гидроэнергетики. Учитывая природу ее источников энергии, многие из электростанций компании расположены в удаленной и труднодоступной местности. Это может создавать проблемы, связанные с контролем и мониторингом удаленных объектов.
Gorenjske Elektrarne начала использовать программное обеспечение SCADA от COPA-DATA в 2006 году, когда в рамках проекта реконструкции гидроэлектростанции Soteska, компании Gorenjske Elektrarne, был использован zenon для локальных систем контроля и мониторинга. Команда Gorenjske Elektrarne осталась довольна улучшенным обзором системы и надежностью zenon.
Юрий Цадеж, Менеджер Проектов в Gorenjske Elektrarne, рассказывает: “zenon прост в установке и чрезвычайно стабилен в эксплуатации. Надежность и уверенность в решении — вот две из множества причин, по которым мы в качестве стандарта выбрали zenon”.
УЛУЧШЕННЫЙ ОБЗОР ПОМОГ ОПТИМИЗИРОВАТЬ ВЫХОДНЫЕ ДАННЫЕСледующий проект реконструкции был проведен в 2007 году на малой гидроэлектростанции (малой ГЭС) Sorica, мощностью 125 кВт. zenon был внедрен в качестве локальной SCADA-системы для контроля операций, записи ключевых параметров станции, полной визуализации ГЭС, оповещения инженеров о тревогах и недостаточно эффективной работе, а также для дальнейшего оперативного анализа и оптимизации.
 Реконструкция системы управления станцией с использованием zenon привела к снижению эксплуатационных затрат на 30% и увеличению производительности на 15% за счет устранения простоев и неэффективной работы.
Реконструкция системы управления станцией с использованием zenon привела к снижению эксплуатационных затрат на 30% и увеличению производительности на 15% за счет устранения простоев и неэффективной работы.Алеш Аджман, директор Gorenjske Elektrarne, рассказывает: «У нас был очень хороший опыт работы с решением от COPA-DATA. Для нас важно было оптимизировать производственные затраты и получить обзор всех эксплуатационных параметров. zenon помог нам достичь этого, что привело к увеличению производительности электростанции и снижению связанных с этим эксплуатационных расходов».
Команда Gorenjske Elektrane внедрила решение для мониторинга и управления на базе zenon внутри компании. Алеш Аджман: “Результат работы команды наглядно демонстрирует эффект, достигнутый после реконструкции — улучшение производительности можно было увидеть сразу после введения проекта в эксплуатацию в конце 2007 года.»
Облако дает быстрое пониманиеGorenjske Elektrarne использует сейчас zenon в сочетании с Microsoft Azure для быстрого и легкого доступа к своему центру управления.
 Теперь информация из центра управления Gorenjske Elektrarne отображается на мобильных клиентах без задержек.
Теперь информация из центра управления Gorenjske Elektrarne отображается на мобильных клиентах без задержек.Сотрудники просто устанавливают удаленные клиенты на свои подключенные к интернету ПК, планшеты или телефоны, получая безопасные доступ к приложению zenon. Без больших вложений и без специального оборудования Gorenjske Elektrarne гарантировала, что оперативный обзор получит каждый сотрудник, нуждающийся в нем. Этот обзор представляет собой информационную панель мониторинга всей инфраструктуры в режиме реального времени по всем 36 распределенным электростанциям.
Инженеры и руководители могут получить доступ к необходимой им информации с помощью своих смартфонов под управлением Android. Запущенное в Azure приложение zenon предоставляет нужную информацию в режиме реального времени. Это позволяет команде реагировать максимально быстро и принимать оптимальные решения на основе надежных и качественных данных.
Юрий Цадеж: “Приложение очень быстрое и отзывчивое. Я очень доволен результатом нашего последнего проекта zenon, использующего платформу Microsoft Azure.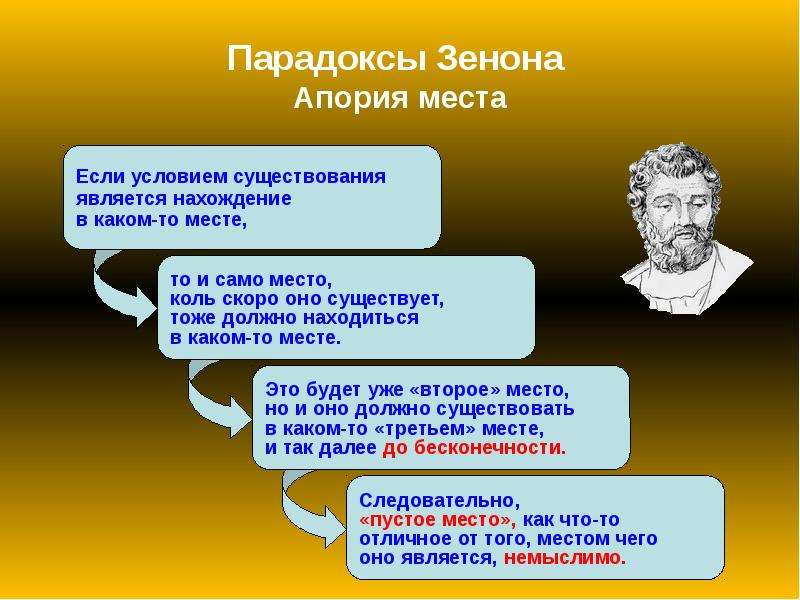 Это очень ценно для нашей компании.”
Это очень ценно для нашей компании.”
Пользователи могут просматривать аварии, события, тренды и отчеты в любое время и из любого места с минимальными усилиями. Azure автоматически подстраивается при необходимости — так что случайные всплески активности в ответ на событие или аварийное состояние полностью поддерживаются без потери производительности.
Юрий Цадеж: “Одной из причин, по которой в качестве стандарта мы выбрали программное обеспечение от COPA-DATA, является отличная техническая подготовленность команды COPA-DATA. Эти знания лежат в основе всего что они делают и у нас есть полная уверенность в их решениях и их пути развития. Мы знаем, что команда COPA-DATA использовать самые перспективные новые технологии уже на ранней стадии, и, более того, они не станут использовать их ради самого использования; но только там, где это приносит реальную ощутимую выгоду для клиентов. Это то, что требуется , чтобы решения zenon были надежными, эффективными и простыми в использовании”.
Проект Sorica положил начало инициативе по совершенствованию централизованного и децентрализованного мониторинга всех операций ГЭС, которая проходила с 2010 по 2013 год. Затем в 2014 и 2015 годах к центральной SCADA-системе были подключены еще 23 фотоэлектрических электростанции. Использовался весь функционал zenon, обеспечивающий отображение рабочих параметров, обработку аварий вывод изображения с камер видеонаблюдения в режиме реального времени в центре управления ГЭС в городе Крань. С использованием веб-сервера и веб-клиента zenon эту информацию можно просмотреть в любом месте, где есть возможность подключения к сети Интернет.
zenon Webserver Pro позволяет операторам, работающим «в поле» удаленно подключаться к центральной SCADA zenon для мониторинга и управления электростанциями из любого места. Это позволило сократить главные эксплуатационные расходы. Понимание предоставляемых zenon данных дало персоналу в штаб-квартире в Кране возможность диагностировать события на электростанциях и подготавливать план действий еще перед отправкой инженеров на объект — экономя драгоценное время и деньги.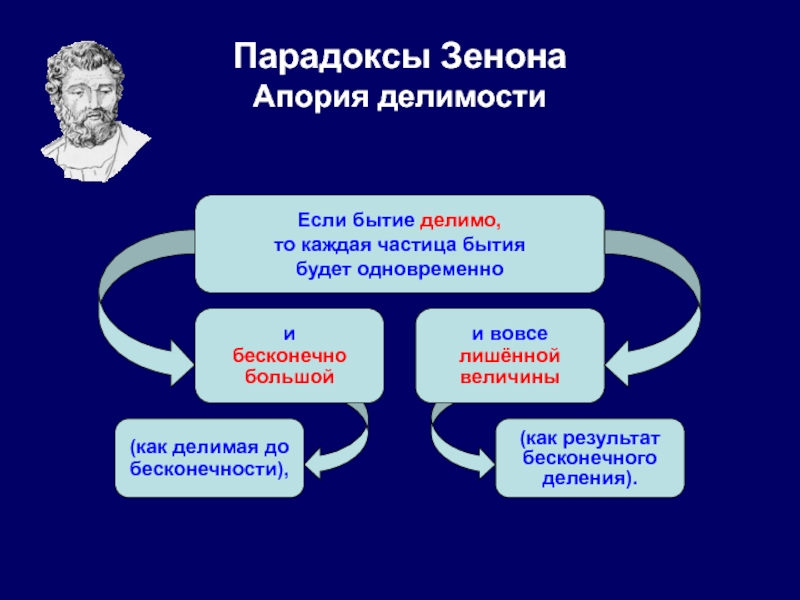
Алеш Аджман рассказывает о дальнейших преимуществах: “Мы ощутили существенные улучшения благодаря данным, полученным после интеграции zenon. Техническое обслуживание было оптимизировано, эксплуатационные расходы уменьшились и уменьшаются и по сей день”.
Юрий Цадеж подтверждает: “100% надежность zenon — это великолепно для нас. Проект оптимизации привел к снижению времени простоев и случаев неэффективной работы. zenon позволяет нам удаленно исследовать и диагностировать проблемы прежде, чем они могут оказать негативное влияние на производство. Из-за рисков, связанных с высоким уровнем воды и паводковыми водами, важно иметь возможность дистанционно контролировать работу, для чего zenon также оказался очень полезен”.
КОММУНИКАЦИОННЫЕ ПРОБЛЕМЫ ТРЕБУЮТ ТВОРЧЕСКИХ РЕШЕНИЙПоследние годы Gorenjske Elektrarne успешно развивает свой бизнес и сейчас владеет и управляет 15 гидроэлектростанциями, 23 фотоэлектрическими установками и тремя установками комбинированного цикла по всей Словении.
 zenon был внедрен во все системы коммунального хозяйства гидроэлектростанций, считывая данные и показатели с ПЛК и обеспечивая необходимый контроль и защиту электростанции.
zenon был внедрен во все системы коммунального хозяйства гидроэлектростанций, считывая данные и показатели с ПЛК и обеспечивая необходимый контроль и защиту электростанции.Учитывая географические ограничения бизнеса, компании Gorenjske Elektrarne было необходимо развернуть комплекс коммуникационных решений, удовлетворяющих их потребностям для создания централизованного обзора всей своей деятельности.
Для Gorenjske Elektrarne было бы непомерно дорого строить свою собственную сеть связи на такой широкой географической территории, поэтому компании пришлось положиться на IP-VPN по арендованным линиям, а в некоторых очень отдаленных местах — по спутниковой связи. Поскольку, в частности, спутниковая связь ненадежна, zenon взял на себя ключевую роль в сетевом мониторинге и безопасности коммуникационного оборудования.
Эти проблемы заставили компанию творчески подойти к вопросу обеспечения надежного и гибкого обзора своей деятельности из любого места. Это привело Gorenjske Elektrarne к изучению возможностей использования zenon в сочетании с Облачной Платформой Azure от Microsoft, включая Azure IoT Suite. Microsoft Azure предлагает масштабируемую платформу для простого и экономичного доступа к корпоративным приложениям из облака.
Microsoft Azure предлагает масштабируемую платформу для простого и экономичного доступа к корпоративным приложениям из облака.
zenon полностью интегрирован с облачными сервисами Microsoft Azure — платформой, разработанной в помощь организациям с целью оценить преимущество масштабируемости, гибкости и экономической эффективности облака без необходимости переписывания приложений. Пользователи получают корпоративные приложения «как есть» на любом устройстве, не переписывая их; устраняя необходимость в крупных финансовых вложениях и сокращая время запуска облачных решений в производстве.
Психологика — Апории Зенона
Дихотомия
Первый вариант апории «Дихотомия»:
Пусть тело должно пройти путь конечной длины. Пусть оно уже прошло половину
пути, отсчитаем эту половину. Далее надо отсчитать половину оставшегося пути,
потом половину той половину и так далее. В результате надо отсчитать бесконечное
число чисел. Представляется невозможным сосчитать бесконечное число величин за
конечное время.
Представляется невозможным сосчитать бесконечное число величин за
конечное время.
На данной схеме нарисовано тело — шар, который должен прокатиться по отрезку конечной длины и отмечены точки деления отрезка пополам:
Конечно, никто не стоит рядом с шаром и не отсчитывает расстояния синхронно с его движением. Имеется в виду, что невозможно просуммировать бесконечное число отрезков за конечное время. Допустим, общая длина пути равна 1 метру. Значит, отрезки будут длиной в 1/2 м, 1/4 м, 1/8 м, 1/16 м и т.д. Чтобы вычислить путь, надо просуммировать длины бесконечного числа отрезков:
1/2 + 1/4 + 1/8 + 1/16 +…
Конечно, во времена Зенона не умели вычислять суммы бесконечных рядов. Но это не значит, что суммы
таких рядов не научились вычислять до сих пор. Подобная последовательность чисел называется
геометрической прогрессией. Ее сумму умел вычислять, например, Ньютон. В школе тоже проходят
эту формулу:
Ее сумму умел вычислять, например, Ньютон. В школе тоже проходят
эту формулу:
Сумма = a / (1 — q)
Где a — первый элемент последовательности (в рассмотренном случае 1/2 = 0,5). q — во сколько раз следующий элемент последовательности больше предыдущего (в рассмотренном случае тоже 0,5). Таким образом, сумма равна 0,5 / (1 — 0,5) = 0,5 / 0,5 = 1. Как видите, все сходится.
В школе приведенная формула может даваться без доказательств. Строгое ее обоснование дается в самом начале курса математического анализа в любом техническом ВУЗе (или в школе с математическим уклоном) в разделах «теория пределов» или «бесконечные последовательности». Каким же образом современные математики доказывают подобную формулу? Неужели они успевают просуммировать бесконечное число слагаемых за свою конечную жизнь? Нет, конечно. Совсем необязательно решать задачу «в лоб».
Я, разумеется, не буду цитировать здесь большой фрагмент учебника математики. Вместо этого я попытаюсь дать
общее представление о доказательстве несколько упрощенно, показав общий принцип.
Вместо этого я попытаюсь дать
общее представление о доказательстве несколько упрощенно, показав общий принцип.
Берется предполагаемый результат суммы (в данном случае 1). Понятно, что при суммировании мы всякий раз будем получать суммы меньше единицы: 1 — 1/2, 1 — 1/4, 1 — 1/8,…. То есть, сумма не может находиться на числовой оси правее единицы.
Затем доказывается, что ни одно число слева от единицы тоже не подходит на роль суммы. Например, если взять число, равное 1 — 1/1000, то это число будет пройдено после 10-го деления отрезка пополам, когда сумма будет равна 1 — 1/1024. Так же можно рассуждать для любого другого числа, сколь угодно близкого к единице, но меньше нее.
Итак, справа от единицы нет ни одного подходящего числа, все они больше, чем нужно. Слева — тоже нет ни одного
числа, все они меньше, чем нужно. Методом исключения выясняется, что искомый результат может быть равен только
единице.
Чем больше величин мы просуммируем, тем ближе будет результат к единице. Оставшееся расстояние никогда не станет нулевым, но можно сделать его сколь угодно маленьким и указать, сколько слагаемых надо просуммировать, чтобы пройти любую заданную точку, близкую к единице.
Подобное действие в математике называется «пределом». В данном случае предел — число 1. Физика Ньютона использует понятие предела для решения многих задач. Например, через пределы определяются понятия скорости и ускорения. Как видите, в конечном счете законы движения в физике определяются через подобные пределы.
Итак, в первом варианте апории ошибка заключается в том, что заранее утверждается невозможность найти сумму. Сумму действительно нельзя найти таким способом, как указано в апории. Однако можно ее найти другим способом.
Второй вариант апории «Дихотомия»:
Для того, чтобы пройти путь конечной длины, надо сначала пройти
половину. Для того, чтобы пройти оставшуюся половину, надо сначала пройти
половину половины. И так далее. В результате надо пройти бесконечное число
половин. Представляется невозможным пройти бесконечное число отрезков
за конечное время.
Для того, чтобы пройти оставшуюся половину, надо сначала пройти
половину половины. И так далее. В результате надо пройти бесконечное число
половин. Представляется невозможным пройти бесконечное число отрезков
за конечное время.
Утверждается, что невозможно пройти бесконечное число отрезков за конечное время. В этом последнем утверждении и кроется ошибка в рассуждении и решение парадокса. Это утверждение о невозможности дается без доказательства, принимается как очевидное. Однако, то, что очевидно, не всегда истинно. Так и в этот раз - утверждение оказалось ложным. Расмотрим вопрос подробнее.
Все отрезки имеют разную длину, каждый последующий вдвое меньше предыдущего. Время,
необходимое для преодоления отрезков, тоже будет уменьшаться. Если наш шар катится
равномерно со скоростью 1 м/c, то первый отрезок будет пройден за полсекунды, второй
— за четверть секунды, третий — за осьмушку и так далее. Если попытаться просуммировать
отрезки времени, то получится та самая формула, которую мы уже видели:
Если попытаться просуммировать
отрезки времени, то получится та самая формула, которую мы уже видели:
1/2 + 1/4 + 1/8 + 1/16 +…
А эта формула, как мы знаем, дает вовсе не бесконечность, а 1. Так что время, необходимое для преодоления бесконечного числа отрезков, конечно (в данном случае 1 секунда).
Почему так получается? Да потому, что количество отрезков бесконечно велико, но время на преодоление каждого отрезка бесконечно мало. Говоря «поэтически», когда бесконечно большое сталкивается с бесконечно малым, то результат может быть и конечным, и бесконечным. В данном случае он конечен. А вот такая сумма будет уже бесконечной:
1/2 + 1/3 + 1/4 + 1/5 +…
А если избегать поэзии, то можно заметить: бесконечность — не является каким-то предметом. Бесконечности
бывают самые разные. Мы уже рассмотрели несколько разновидностей. В конкретных случаях надо рассматривать
конкретные формулы для той или иной бесконечности и доказывать свои суждения вместо того, чтобы заявлять:
«это невозможно».
Итак, во втором варианте апории ошибка заключается в том, утверждается невозможность пройти бесконечное число отрезков за конечное время. На самом деле это иногда возможно при условии, что сами отрезки бесконечно малы.
Третий вариант апории «Дихотомия»:
Для того, чтобы тело прошло путь конечной длины, оно должно сначала коснуться места посредине пути. Для того, чтобы пройти оставийся путь, тело должно сначала коснуться места посредине оставшегося пути. И так далее. В результате тело должно коснуться бесконечного числа мест. Представляется невозможным коснуться бесконечного число числа мест за конечное время.
Этот вариант похож на предыдущий, только взамен преодоления отрезков
предлагается «касаться мест». Ошибка также кроется в последнем утверждении. Оно
бездоказательно. Хотя кому-то оно может показаться очевидным, но на деле
оказывается ложным.
Чтобы коснуться точки на полпути шару нужно полсекунды. До следующей точки он доберется еще за четверть секунды. До следующей — за осьмушку и так далее. Да, число точек бесконечно велико, но время, нужное для касания каждой точки, бесконечно мало. Когда бесконечно малое сталкивается с бесконечно большим, результат не обязательно получится бесконечным. В данном случае он конечен.
Ахиллес и черепаха
Быстроногий Ахиллес никогда не сможет догнать черепаху, поскольку Ахиллесу необходимо сначала добежать до места, откуда начала движение черепаха, а она за это время немного уползет вперед до нового места. Ахиллес будет должен добежать до этого нового места, но черепаха за это время хоть немного, но уползет вперед. В результате окажется, что черепаха всегда будет на какое-то расстояние опережать Ахиллеса.
Ошибка тут точно такая же, как и в апории «Дихотомия». Утверждается (бездоказательно), что
«черепаха всегда будет опережать», но что значит «всегда»? Бесконечное время? Однако,
Ахиллес бежит быстрее. На рисунке видно, что каждый раз ему требуется преодолеть меньшее
расстояние, чем на предыдущем шаге. То есть, время «догоняния» — бесконечно малая величина.
А когда бесконечно большое (число «догоняний») сталкивается с бесконечно малым (временем
«догоняния») то результат (общее время погони) не обязан быть бесконечным. Он и не
бесконечен.
Утверждается (бездоказательно), что
«черепаха всегда будет опережать», но что значит «всегда»? Бесконечное время? Однако,
Ахиллес бежит быстрее. На рисунке видно, что каждый раз ему требуется преодолеть меньшее
расстояние, чем на предыдущем шаге. То есть, время «догоняния» — бесконечно малая величина.
А когда бесконечно большое (число «догоняний») сталкивается с бесконечно малым (временем
«догоняния») то результат (общее время погони) не обязан быть бесконечным. Он и не
бесконечен.
Допустим, что Ахиллес бежит в 10 раз быстрее (со скоростью 10 м/c) и расстояние до черепахи равно сначала 1000 метрам. Эти 1000 метров он пробежит за 100 секунд. Шустрая черепаха тем временем преодолеет 100 метров. Эти 100 метров Ахиллес пробежит за 10 секунд. Черепаха уйдет вперед на 10 метров. Эти 10 метров Ахиллес пробежит за 1 секунду. Получаем сумму:
100 + 10 + 1 + 1/10 + 1/100 +…
Снова имеем геометрическую прогрессию. Применим уже знакомую формулу:
a / (1 — q) = 100 / (1 — 1/10) = 100 / (9/10) = 1000/9
Как видите, время вовсе не бесконечно, если его подсчитать, а не голословно утверждать, дескать, «никогда».
Стрела
В двух предыдущих случаях Зенон исходил из предположения, что время и расстояние можно делить бесконечно. Как сказали бы в наше время, время и пространство непрерывны. А что, если время и пространство состоят из мельчайших кирпичиков, и делить можно только до определенного предела — до этих кирпичиков? Примерно как кусок железа можно разделить до атомов, но не более того (если делить дальше, это будет уже не железо) или как изображением на экране компьютера можно управлять с точностью только до пиксела.
Я недаром упомянул изображение на компьютере. Движущиеся фигурки на экране монитора — отличная иллюстрация
дискретного пространства и времени. Расстояния определяются с точностью до 1 пиксела, и более мелкими деталями
изображения мы управлять не можем. Время тоже определяется с точностью до 1 кадра (например 1/100 секунды если
монитор имеет частоту развертки 100 Герц). Компьютерная графика поможет нам понять логику решения двух других
парадоксов Зенона. Рассмотрим их.
Расстояния определяются с точностью до 1 пиксела, и более мелкими деталями
изображения мы управлять не можем. Время тоже определяется с точностью до 1 кадра (например 1/100 секунды если
монитор имеет частоту развертки 100 Герц). Компьютерная графика поможет нам понять логику решения двух других
парадоксов Зенона. Рассмотрим их.
Пусть время делится на отдельные кадры. неподвижная стрела в каждом кадре занимает место, равное ее длине. Летящая стрела в каждом кадре также занимает место, равное ее длине, а значит, не летит, а покоится.
Аристотель предлагает такое решение этого парадокса: давайте, мол, не будем признавать, что время делится на отдельные моменты. Но это — не решение, а уход от него. Мы решим парадокс «честно». Пусть время состоит из отдельных минимальных фрагментов (как кадры на экране монитора). Где тогда ошибка в парадоксе?
А вот она: «а значит, не летит, а покоится. » Из того, что летящая стрела имеет некоторое общее свойство с
неподвижной стрелой (занимать место, равное ее длине) нельзя делать вывод, что речь идет в обоих случаях
об одинаковых стрелах. Ведь другие свойства могут оказаться различными! И в самом деле: между стрелами
есть разница: если неподвижная стрела занимает в каждом кадре одни и те же 100 пикселов, то летящая
стрела может в следующем кадре занимать другие 100 пикселов. По этому свойству стрелы различаются.
» Из того, что летящая стрела имеет некоторое общее свойство с
неподвижной стрелой (занимать место, равное ее длине) нельзя делать вывод, что речь идет в обоих случаях
об одинаковых стрелах. Ведь другие свойства могут оказаться различными! И в самом деле: между стрелами
есть разница: если неподвижная стрела занимает в каждом кадре одни и те же 100 пикселов, то летящая
стрела может в следующем кадре занимать другие 100 пикселов. По этому свойству стрелы различаются.
Здесь мы видим еще одно подтверждение правила «аналогии лгут». Нелогично из сходства объектов в одном свойстве делать вывод о сходстве по всем свойствам.
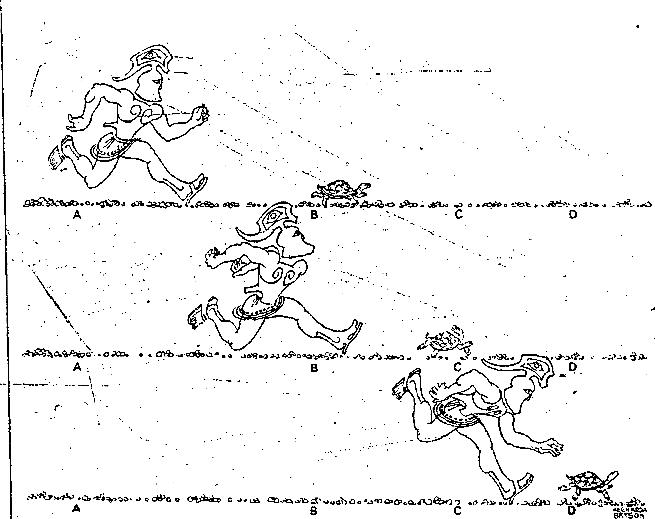
Стадион
Апория «Стадион» (в приведенном выше фрагменте перевода не стадион, а ристалище) также рассматривает ситуацию, когда время нельзя делить до бесконечности, а только до минимального фрагмента (кадра).
Пусть есть три группы предметов, одинаковых по количеству (N штук). Один ряд «A» стоит на месте. Второй ряд «B» марширует
мимо него слева направо, а третий ряд «C» марширует мимо первого ряда справа налево. Пусть ряд «B» минует за один кадр
одного из ряда «A», так что ему требуется N кадров. Также ряду «C» надо N кадров, чтобы пройти мимо ряда «B». Но второй
и третий ряды маршируют навстречу друг другу, так что должны миновать друг друга за время, вдвое меньшее — N/2 кадров.
Один ряд «A» стоит на месте. Второй ряд «B» марширует
мимо него слева направо, а третий ряд «C» марширует мимо первого ряда справа налево. Пусть ряд «B» минует за один кадр
одного из ряда «A», так что ему требуется N кадров. Также ряду «C» надо N кадров, чтобы пройти мимо ряда «B». Но второй
и третий ряды маршируют навстречу друг другу, так что должны миновать друг друга за время, вдвое меньшее — N/2 кадров.
В качестве движущихся предметов возьмем следующих друг за другом лошадей. На рисунке вы видите 6 последовательных кадров. Верхний ряд лошадей «A» стоит на месте. Следующий ряд «B» идет справа налево. И самый нижний ряд «C» движется слева направо. Обратите внимание на первую лошадь во ряду «B». На кадрах 2, 3, 4 и 5 она побывала перед каждой из лошадей ряда A. Однако она успела побывать только перед двумя лошадьми из ряда «C» (на кадрах 4 и 5).
Ошибку в этом парадоксе нашел сам Аристотель в своем пересказе. Как он правильно
заметил, утверждается, что «величина, двигаясь с равной скоростью один раз мимо движущегося, другой раз
мимо покоящегося [тела], затрачивает на это равное время, но это неверно».
Лошадь из ряда «B» за один кадр минует не одну, а сразу две лошади из ряда «C».
Как он правильно
заметил, утверждается, что «величина, двигаясь с равной скоростью один раз мимо движущегося, другой раз
мимо покоящегося [тела], затрачивает на это равное время, но это неверно».
Лошадь из ряда «B» за один кадр минует не одну, а сразу две лошади из ряда «C».
Таким образом, причина этого парадокса — ложное утверждение «Также ряду «C» надо N кадров, чтобы пройти мимо ряда «B». Можно догадаться, откуда оно взялось. Если рассматривать непрерывное движение, то каждая лошадь ряда B обязательно побывает перед каждой лошадью ряда C. Этот факт распространяется и на дискретное движение. В результате имеем скрытое смешивание двух разных моделей и противоречие. Правильное рассуждение соответствует рисунку.
В заключение отмечу тот факт, что логические ошибки, лежащие в основе парадоксов, могли быть обнаружены еще
во времена Зенона. Например, тогда не умели считать сумму бесконечной геометрической прогрессии, но можно было
заметить, что утверждение «чтобы преодолеть бесконечное число отрезков, требуется бесконечное время» — принимается
без доказательства.
Судя по приведенным фрагментам, Аристотель пытался разобраться с этим вопросом. Можно услышать такие мнения, что Зенон пытался опровергнуть апориями (так сказать, «от противного») какие-то заблуждения современников. Это, конечно, — досужие домыслы, поскольку все, что у нас есть — пересказ Аристотеля. В любом случае в рассуждениях апорий имеются логические ошибки, которые не позволяют применять их даже для доказательства «от противного».
Зенон Элейский — Учебный центр — Корпоративное обучение
Зенон Элейский/Zenon Eleiski
|
Притворяясь, что не слышу хулы, я не замечу и похвалы. Зенон Элейский |
Зенон Элейский — древнегреческий философ, представитель Элейской школы, ученик Парменида. Аристотель назвал Зенона создателем диалектики, искусства выдвигать аргументы и опровергать чужие мнения. Для защиты учения Парменида о едином неподвижном бытии Зенон сформулировал ряд апорий («неразрешимых положений»), показав, что признание реальности множественности и движения ведет к логическим противоречиям. Из четырех десятков апорий наиболее известны апории о движении: «Дихотомия», «Ахилл и черепаха», «Стрела и Стадий» (Движущиеся тела). Все эти апории представляют собой доказательства от противного. Вместе с вариантом их решения изложены у Аристотеля.
Аристотель назвал Зенона создателем диалектики, искусства выдвигать аргументы и опровергать чужие мнения. Для защиты учения Парменида о едином неподвижном бытии Зенон сформулировал ряд апорий («неразрешимых положений»), показав, что признание реальности множественности и движения ведет к логическим противоречиям. Из четырех десятков апорий наиболее известны апории о движении: «Дихотомия», «Ахилл и черепаха», «Стрела и Стадий» (Движущиеся тела). Все эти апории представляют собой доказательства от противного. Вместе с вариантом их решения изложены у Аристотеля.
В первых двух («Дихотомия» и «Ахилл и черепаха») предполагается бесконечная делимость пространства. Так, как бы быстро ни бежал Ахилл, он никогда не догонит медленную черепаху, потому что за то время, которое ему потребуется для того, чтобы пробежать половину намеченного пути, черепаха, двигаясь без остановки, всегда будет отползать еще немного, и этот процесс не имеет завершения, ибо пространство делимо до бесконечности. В двух других апориях рассматривается несводимость непрерывности пространства и времени к неделимым «местам» и «моментам». Летящая стрела во всякий фиксируемый момент времени занимает определенное место, равное своей величине – получается, что в рамках самого неделимого момента она «покоится», и тогда получается, что движение стрелы состоит из суммы состояний покоя, что абсурдно. Следовательно, стрела на самом деле не движется. На протяжении всей дальнейшей истории апории Зенона являются предметом внимания и споров среди философов, логиков, математиков (Лейбниц, Кант, Коши, теория множеств Кантора).
Апории Зенона Элейского явились важнейшим этапом на пути развития античной диалектики. Они оказали существенное влияние и на развитие философии в новое время, в частности на философское обоснование математики.
Зенон Элейский и античная философия
Зенон был учеником Парменида. Как говорит Платон в «Пармениде» он был высокого роста.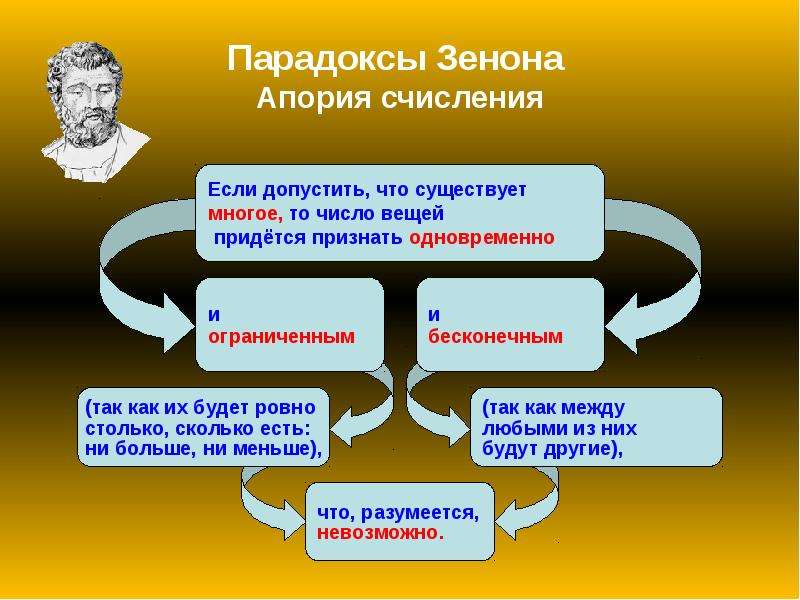 Тот же Платон в «Софисте» называет его «Элейским Паламедом». По словам Аристотеля, он был изобретателем диалектики, как Эмпедокл — риторики. Был он человеком исключительных достоинств и в философии, и в политической жизни, сохранились его книги, полные большого ума.
Тот же Платон в «Софисте» называет его «Элейским Паламедом». По словам Аристотеля, он был изобретателем диалектики, как Эмпедокл — риторики. Был он человеком исключительных достоинств и в философии, и в политической жизни, сохранились его книги, полные большого ума.
Помимо прочих доблестей, Зенон отличался презрением к сильным мира сего, не уступая в этом Гераклиту.
Рассказывают, что он возмутился, когда его хулили, а в ответ на чей-то упрек сказал: «Притворяясь, что не слышу хулы, я не замечу и похвалы».
Аргументы Зенона привели к кризису древнегреческой математики, преодоление которого было достигнуто только атомистической теорией Демокрита. Основная мысль апорий Зенона (как и Парменида) состоит в том, что прерывность, множественность, движение характеризуют картину мира, как она воспринимается чувствами. Диалектика Зенона основывалась на постулате недопустимости противоречий в достоверном мышлении: появление противоречий, возникающих при предпосылке мыслимости множественности, прерывности и движения, рассматривается как свидетельство ложности самой предпосылки и в то же время свидетельствует об истинности противоречащих ей положений о единстве, непрерывности и неподвижности мыслимого (а не чувственно воспринимаемого) бытия.
Критику аргументов Зенона с позиций идеалистической диалектики дал Гегель.
Со времен Пифагора время и пространство рассматривались, с математической точки зрения, как составленные из множества точек и моментов. Однако они обладают также свойством, которое легче ощутить, нежели определить, а именно «непрерывностью». С помощью ряда парадоксов Зенон стремился доказать невозможность разделения непрерывности на точки или моменты. Его рассуждение сводится к следующему: предположим, что деление проведено нами до конца. Тогда верно одно из двух: либо мы имеем в остатке наименьшие возможные части или величины, которые неделимы, однако бесконечны по своему количеству, либо деление привело нас к частям, не имеющим величины, т.е. обратившимся в ничто, ибо непрерывность, будучи однородной, должна быть делимой повсюду, а не так, чтобы в одной своей части быть делимой, а в другой – нет. Однако оба результата нелепы: первый потому, что процесс деления нельзя считать законченным, пока в остатке – части, обладающие величиной, второй потому, что в таком случае изначальное целое было бы образовано из ничто. Симплиций приписывает это рассуждение Пармениду, однако кажется более вероятным, что оно принадлежит Зенону. В более полном виде этот довод против множественности неделимых величин приводит Филопон: «Зенон, поддерживая своего учителя, старался доказать, что все сущее должно быть единым и неподвижным. Доказательство свое он основывал на бесконечной делимости любой непрерывности. Именно, утверждал он, если сущее не будет единым и неделимым, но может делиться на множество, единого по сути вообще не будет (ибо если непрерывность можно делить, это будет означать, что ее можно делить до бесконечности), а если ничто не будет по сути единым, невозможно и множество, поскольку множество составлено из многих единиц. Итак, сущее не может быть разделено на множество, следовательно, есть только единое. Это доказательство может строиться и по-другому, а именно: если не будет сущего, которое неделимо и едино, не будет и множества, ибо множество состоит из многих единиц. А ведь каждая единица либо едина и неделима, либо сама делится на множество.
Симплиций приписывает это рассуждение Пармениду, однако кажется более вероятным, что оно принадлежит Зенону. В более полном виде этот довод против множественности неделимых величин приводит Филопон: «Зенон, поддерживая своего учителя, старался доказать, что все сущее должно быть единым и неподвижным. Доказательство свое он основывал на бесконечной делимости любой непрерывности. Именно, утверждал он, если сущее не будет единым и неделимым, но может делиться на множество, единого по сути вообще не будет (ибо если непрерывность можно делить, это будет означать, что ее можно делить до бесконечности), а если ничто не будет по сути единым, невозможно и множество, поскольку множество составлено из многих единиц. Итак, сущее не может быть разделено на множество, следовательно, есть только единое. Это доказательство может строиться и по-другому, а именно: если не будет сущего, которое неделимо и едино, не будет и множества, ибо множество состоит из многих единиц. А ведь каждая единица либо едина и неделима, либо сама делится на множество. Но если она едина и неделима, Вселенная составлена из неделимых величин, если же единицы сами подлежат делению, мы будем задавать тот же самый вопрос относительно каждой из подлежащих делению единиц, и так до бесконечности. Таким образом, если существующие вещи множественны, Вселенная окажется образованной бесконечным числом бесконечностей. Но поскольку этот вывод нелеп, сущее должно быть единым, а быть множественным ему невозможно, ведь тогда придется каждую единицу делить бесконечное число раз, что нелепо».
Но если она едина и неделима, Вселенная составлена из неделимых величин, если же единицы сами подлежат делению, мы будем задавать тот же самый вопрос относительно каждой из подлежащих делению единиц, и так до бесконечности. Таким образом, если существующие вещи множественны, Вселенная окажется образованной бесконечным числом бесконечностей. Но поскольку этот вывод нелеп, сущее должно быть единым, а быть множественным ему невозможно, ведь тогда придется каждую единицу делить бесконечное число раз, что нелепо».
Аристотель вновь и вновь разрешает парадоксы Зенона как для геометрии, так и для физики, утверждая, что бесконечно малое существует лишь в потенции, но не в реальности. Для современной математики такой ответ неприемлем. Современный анализ бесконечности, в особенности в трудах Г.Кантора, привел к определению континуума, лишающему антиномии Зенона парадоксальности.
Источники:
http://www.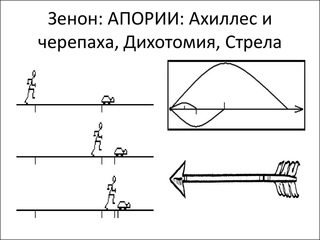 krugosvet.ru
krugosvet.ru
http://www.chronos.msu.ru
http://ru.wikipedia.org
http://slovari.yandex.ru
(PDF) Квантовый эффект Зенона проявляется поэтапно
6
«Топологический переход в геометрических фазах, индуцированных измерениями», Труды Национальной академии наук.
ences 117, 5706–5713 (2020) .
[20] Кирилл Снижко, Парвин Кумар, Нихал Рао и Юваль
Гефен, «Асимметричный дефаз, вызванный слабым измерением —
ing: топологический переход», (2020), arXiv: 2006.13244.
[21] Кирилл Снижко, Нихал Рао, Парвин Кумар и Юваль
Гефен, «Фазы и дефазы, вызванные слабыми измерениями —
ing: нарушение симметрии геометрической фазы», (2020),
arXiv: 2006 г.14641.
[22] Яодун Ли, Сяо Чен и Мэтью П. А. Фишер,
«Квантовый эффект Зенона и переход многочастичной запутанности —
», Phys. Ред. B 98, 205136 (2018),
arXiv: 1808.06134.
[23] Амос Чан, Рахул М. Нандкишор, Майкл Претко,
и Грэм Смит, «Динамика унитарной проективной запутанности —
», Phys. Ред. B 99, 224307 (2019),
arXiv: 1808.05949.
[24] Брайан Скиннер, Джонатан Рухман и Адам Нахум,
«Фазовые переходы, вызванные измерениями в динамике запутывания
», Phys.Ред. X 9, 031009 (2019),
arXiv: 1808.05953.
[25] M. Szyniszewski, A. Romito и H. Schomerus,
«Переход зацепления из измерений слабой
переменной силы», Phys. Ред. B 100, 064204 (2019),
arXiv: 1903.05452.
[26] ZK Minev, SO Mundhada, S. Shankar, P. Reinhold,
R. Gutiérrez-Jáuregui, RJ Schoelkopf, M. Mirrahimi,
HJ Carmichael, и MH Devoret, «Чтобы поймать и перевернуть
. квантовый скачок в полете », Nature 570, 200–
204 (2019).
[27] Б. Мисра и Е. К. Сударшан, «Парадокс Зенона
в квантовой теории», J. Math. Phys. 18, 756–763 (1977).
[28] Ашер Перес, «Парадокс Зенона в квантовой теории», Am. J.
J.
Phys. 48, 931–932 (1980).
[29] П. Факки, С. Паскацио, «Квантовые подпространства Зенона»,
Phys. Rev. Lett. 89, 080401 (2002).
[30] П. Факки, А.Г. Кляйн, С. Паскацио, Л.С. Schulman,
«Фаза Берри из квантового эффекта Зенона», Phys.Lett.
A257, 232–240 (1999).
[31] Даниэль Бургарт, Паоло Факки, Витторио Джованнетти, Хи-
Ромичи Наказато, Саверио Паскацио и Казуя Юаса,
«Неабелевы фазы из квантовой динамики Зенона»,
Phys. Ред. A 88, 042107 (2013).
[32] Стефано Герардини, Шамик Гупта, Франческо Саверио
Каталиотти, Аугусто Смерци, Филиппо Карузо и Сте-
фано Руо, «Стохастический квантовый Зенон с большим отклонением
теория», Нью Дж.Phys. 18, 013048 (2016).
[33] Т. Дж. Эллиотт и В. Ведрал, «Квантовая квази-зеноди-
динамика: переходы, опосредованные частыми проективными
измерениями вблизи режима Зенона», Phys. Ред. A 94,
012118 (2016).
[34] Мехвиш Маджид и Адам Заман Чаудри, «
квантовые эффекты Зенона и анти-Зенона с неселективными
проективными измерениями», Sci. Отчет 8, 14887 (2018).
Отчет 8, 14887 (2018).
[35] П. Г. Квиат, А. Г. Уайт, Дж. Р. Митчелл, О.Nairz,
G. Weihs, H. Weinfurter и A. Zeilinger, «Квантовые опрашивающие измерения высокой эффективности
с помощью квантового эффекта Зенона
», Phys. Rev. Lett. 83, 4725–4728
(1999), arXiv: 93 [Quant-ph].
[36] М. К. Фишер, Браулио Гутьеррес-Медина и М. Г.
Райзен, «Наблюдение квантового Зенона и анти-
эффектов Зенона в нестабильной системе», Phys. Rev. Lett.
87, 040402 (2001).
[37] Яник Уолтерс, Макс Штраус, Рольф Симон Шенфельд и
Оливер Бенсон, «Квантовое явление Зенона на одном твердотельном спине
», Phys.Ред. A 88, 020101 (R) (2013).
[38] Адриен Синьолес, Адриен Факон, Дориан Гроссо, Игорь Дот-
сенко, Серж Харош, Жан-Мишель Раймон, Мишель
Брюн и Себастьян Глейз, «Конфиденциальная квантовая динамика стрелы Зенона
наблюдалась на , ”Нат. Phys. 10,
715–719 (2014).
[39] F. Schäfer, I. Herrera, S. Cherukattil, C. Lovecchio, F.S.
Schäfer, I. Herrera, S. Cherukattil, C. Lovecchio, F.S.
Каталиотти, Ф. Карузо и А. Смерци, «Экспериментальная переработка
квантовой дзено-динамики», Nat.Commun. 5,
3194 (2014).
[40] Дэвид Лейден, Эдуардо Мартин-Мартинес и Ахим
Кемпф, «Совершенный зено-подобный эффект за счет несовершенных измерений
на конечной частоте», Phys. Ред. A 91, 022106
(2015).
[41] Манчао Чжан, Чунван Ву, И Се, Вей Ву и
Пинксин Чен, «Квантовый эффект Зенона по неполным
измерениям», Quantum Inf. Процесс. 18, 97 (2019).
[42] Фусян Ли, Цзе Рен и Николай А.Синицын, «Квантовый эффект Зенона
как топологический фазовый переход в полной статистике
и спектроскопия спинового шума», EPL (Euro-
Physics Lett. 105, 27001 (2014).
[43] Карло Пресилья) , Роберто Онофрио и Убальдо Тамбини,
«Измерение квантовой механики и экспериментов по квантовому эффекту Зенона
», Ann. Phys. (N. Y), 248, 95–121
Y), 248, 95–121
(1996).
[44] Гурвиц С.А., Федичкин Л., Мозырский Д., Берман Г.П.
, “Релаксация и эффект Зенона в измерениях Qubit Mea-
”, УФН.Rev. Lett. 91, 066801 (2003).
[45] Казуки Кошино и Акира Симидзу, «Квантовый эффект Зенона
по общим измерениям», Phys. Реп. 412, 191–275
(2005).
[46] А. Чантасри, Дж. Дрессел и А. Н. Джордан, «Принцип действия
для непрерывных квантовых измерений», Phys. Ред.
A88, 042110 (2013).
[47] Парвин Кумар, Алессандро Ромито и Кирило
Снижко, «Квантовый эффект Зенона с частичным измерением
и зашумленной динамикой» (2020), arXiv: 2006.13970.
[48] Руско Русков, Ари Мизель, Александр Н. Коротков,
«Кроссовер динамики фазового кубита в присутствии
— слабое измерение с отрицательным результатом», Phys. Ред. B 75,
220501 (R) (2007).
[49] Цзяминг Ли, Тишо Ван, Ле Луо, Срейя Вемури и
Йогеш Н. Джоглекар, «Объединение квантовых эффектов Зенона
Зенона и переходов, нарушающих симметрию четности и времени». ), arXiv: 2004.01364.
), arXiv: 2004.01364.
[50] И-Сян Чен и Тодд А.Брун, «Непрерывное обнаружение и подавление ошибок кванта
с попарными локальными взаимодействиями
», (2020), arXiv: 2004.07285.
[51] Йонг-Су Ким, Чон-Чан Ли, Осун Квон и Юн-
Хо Ким, «Защита запутанности от декогеренции с помощью
слабых измерений и обратного квантового измерения
сал», Nat. Phys. 2012. Т. 8. С. 117–120.
[52] Фактически, это следует из Ур. (12) следует, что ∂λ¯sz (t) ≥0 для любого
t≥0 при λ> 2.
Многотельный квантовый эффект Зенона и индуцированный измерениями переход субизлучения — Quantum
Хорошо известно, что, многократно измеряя квантовую систему, можно полностью заморозить ее динамику до четко определенного состояния, что является признаком квантового эффекта Зенона. . Здесь мы показываем, что для системы многих тел, развивающейся при конкурирующей унитарной эволюции и измерениях переменной силы, начало эффекта Зенона принимает форму резкого фазового перехода. Используя цепочку Quantum Ising с непрерывным мониторингом поперечной намагниченности в качестве парадигматического примера, мы показываем, что для слабых измерений запутанность, создаваемая унитарной динамикой, остается защищенной и фактически усиливается мониторингом, в то время как только выше определенного порога система резко переводится в некоррелированное состояние Зенона.Мы показываем, что этот переход невидим для средней динамики, но закодирован в редких флуктуациях процесса стохастических измерений, которые, как мы показываем, полностью улавливаются неэрмитовым гамильтонианом, который принимает форму квантовой модели Изинга в мнимо-значном поперечное поле. Мы предоставляем аналитические результаты, основанные на фермионизации неэрмитова гамильтониана, в поддержку наших точных численных расчетов.
Используя цепочку Quantum Ising с непрерывным мониторингом поперечной намагниченности в качестве парадигматического примера, мы показываем, что для слабых измерений запутанность, создаваемая унитарной динамикой, остается защищенной и фактически усиливается мониторингом, в то время как только выше определенного порога система резко переводится в некоррелированное состояние Зенона.Мы показываем, что этот переход невидим для средней динамики, но закодирован в редких флуктуациях процесса стохастических измерений, которые, как мы показываем, полностью улавливаются неэрмитовым гамильтонианом, который принимает форму квантовой модели Изинга в мнимо-значном поперечное поле. Мы предоставляем аналитические результаты, основанные на фермионизации неэрмитова гамильтониана, в поддержку наших точных численных расчетов.
Как наблюдатель влияет на судьбу квантовой системы — это фундаментальный давний вопрос в квантовой теории.Недавние успехи в экспериментальной манипуляции с большими ансамблями частиц в квантовом режиме сделали этот вопрос актуальным также для расширенных систем, связанных с измерительной аппаратурой..jpg) В этой работе мы изучаем возникновение фазы Зенона, вызванное скоростью измерения в прототипной цепочке со спином 1/2 с непрерывным мониторингом. Мы показываем, что начало режима Зенона является резким и закодировано в редких событиях стохастической динамики. Последние управляются неэрмитовым гамильтонианом с субизлучением.
В этой работе мы изучаем возникновение фазы Зенона, вызванное скоростью измерения в прототипной цепочке со спином 1/2 с непрерывным мониторингом. Мы показываем, что начало режима Зенона является резким и закодировано в редких событиях стохастической динамики. Последние управляются неэрмитовым гамильтонианом с субизлучением.
[1] Ховард М. Уайзман и Джерард Дж. Милберн «Квантовые измерения и управление» Издательство Кембриджского университета (2009).
https: / / doi.org/ 10.1017 / CBO9780511813948
[2] Б. Мисраанд Э. К. Г. Сударшан. «Парадокс Зенона в квантовой теории», журнал математической физики 18, 756–763 (1977).
https: / / doi.org/ 10.1063 / 1.523304
[3] Ашер Перес «Парадокс Зенона в квантовой теории», Американский журнал физики 48, 931–932 (1980).
https: // doi.org / 10.1119 / 1.12204
[4] Уэйн М. Итано, Д. Дж. Хайнцен, Дж. Дж. Боллинджер и Д. Дж. Винеланд, «Квантовый эффект Зенона», Phys. Ред. A 41, 2295–2300 (1990).
https: / / doi. org/ 10.1103 / PhysRevA.41.2295
org/ 10.1103 / PhysRevA.41.2295
[5] П. Факки, Х. Наказато и С. Паскацио, «От квантового Зенона к обратному квантовому эффекту Зенона» Phys. Rev. Lett. 86, 2699–2703 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.86.2699
[6] П. Факкианд С. Паскацио «Квантовые подпространства Зенона» Phys.Rev. Lett. 89, 080401 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.89.080401
[7] Адриен Синьолес, Адриен Факон, Дориан Гроссо, Игорь Доценко, Серж Гарош, Жан-Мишель Раймон, Мишель Брюн и Себастьян Глейз, «Ограниченная квантовая динамика Зенона наблюдаемой атомной стрелы» Nature Physics 10, 715–719 (2014).
https: / / doi.org/ 10.1038 / nphys3076
[8] Кирилл Снижко, Парвин Кумар и Алессандро Ромито, «Квантовый эффект Зенона проявляется поэтапно» Phys.Ред. Исследование 2, 033512 (2020).
https: / / doi.org/ 10.1103 / PhysRevResearch.2.033512
[9] Л. М. Дуан, М. Д. Лукин, Дж. И. Чирак, П. Золлер, «Квантовая связь на большие расстояния с атомными ансамблями и линейной оптикой. ‘Nature 414, 413–418 (2001).
‘Nature 414, 413–418 (2001).
https: / / doi.org/ 10.1038 / 35106500
[10] Андерс С. Соренсен и Клаус Мёльмер «Запутанность, индуцированная измерениями и квантовые вычисления с атомами в оптических полостях» Phys. Rev. Lett. 91, 097905 (2003).
https: / / doi.org/ 10.1103 / PhysRevLett.91.097905
[11] К.В. Чоу, Х. де Ридматтен, Д. Фелинто, С.В. Поляков, С.Дж. ван Энк и Х.Дж. Кимбл, «Измерение- индуцированная запутанность для возбуждения, хранящегося в удаленных атомных ансамблях »Nature 438, 828–832 (2005).
https: / / doi.org/ 10.1038 / nature04353
[12] Н. Рох, М. Е. Шварц, Ф. Моцой, К. Маклин, Р. Виджай, А. В. Эддинс, А. Н. Коротков, К. Б. Уэйли, М. Саровар, И. Сиддики, «Наблюдение вызванной измерениями запутанности и квантовых траекторий удаленных сверхпроводящих кубитов» Phys.Rev. Lett. 112, 170501 (2014).
https: / / doi.org/ 10.1103 / PhysRevLett.112.170501
[13] Джиа Конг, Рикардо Хименес-Мартинес, Хариклея Труллину, Вито Джованни Лучиверо, Геза Тот и Морган В. Митчелл, «Измерение. -индуцированная пространственно-расширенная запутанность в горячей сильно взаимодействующей атомной системе », Nature Communications 11, 2415 (2020).
Митчелл, «Измерение. -индуцированная пространственно-расширенная запутанность в горячей сильно взаимодействующей атомной системе », Nature Communications 11, 2415 (2020).
https: / / doi.org/ 10.1038 / s41467-020-15899-1
[14] Н. Сьяссен, Д. М. Бауэр, М. Леттнер, Т. Фольц, Д. Дитце, Дж.Дж. Гарсия-Риполь, Дж. И. Чирак, Г. Ремпе и С. Дюрр, «Сильная диссипация препятствует потерям и вызывает корреляции в холодных молекулярных газах» Science 320, 1329–1331 (2008).
https: / / doi.org/ 10.1126 / science.1155309
https: / / science.sciencemag.org/ content / 320/5881/1329
[15] Патил Ю.С., С. Чакрам, М. Венгалатторе, « Вызванная измерениями локализация ультрахолодного решеточного газа » Phys. Rev. Lett. 115, 140402 (2015).
https: // doi.org/ 10.1103 / PhysRevLett.115.140402
[16] Генрих Фремл, Алессио Чиоккетта, Коринна Коллат и Себастьян Диль, «Квантовый эффект Зенона, индуцированный флуктуациями», Phys. Rev. Lett. 122, 040402 (2019).
https: / / doi. org/ 10.1103 / PhysRevLett.122.040402
org/ 10.1103 / PhysRevLett.122.040402
[17] Генрих Фромль, Кристофер Макель, Коринна Коллат, Алессио Чиоккетта и Себастьян Диль, «Ультрахолодные квантовые провода с локализованными потерями: многие- телесный квантовый эффект Зенона » Phys. Ред. B 101, 144301 (2020).
https: // doi.org/ 10.1103 / PhysRevB.101.144301
[18] П.Л. Крапивский, Кироне Маллик и Дрис Селс, «Свободные фермионы с локализованным источником» J. Stat. Мех. Теория Exp. 2019, 113108 (2019).
https: / / doi.org/ 10.1088 / 1742-5468 / ab4e8e
[19] П.Л. Крапивский, Кироне Маллик и Дрис Селс, «Свободные бозоны с локализованным источником» J. Stat. Мех. Теория Exp. 2020, 063101 (2020).
https: / / doi.org/ 10.1088 / 1742-5468 / ab8118
[20] Яодун Ли, Сяо Чен и Мэтью П.А. Фишер, « Квантовый эффект Зенона и многочастичный переход запутанности » Phys. Ред. B 98, 205136 (2018).
https: / / doi.org/ 10.1103 / PhysRevB.98.205136
[21] Брайан Скиннер, Джонатан Рухман и Адам Нахум, «Фазовые переходы, вызванные измерениями в динамике запутанности», Phys. Ред. X 9, 031009 (2019).
Ред. X 9, 031009 (2019).
https: / / doi.org/ 10.1103 / PhysRevX.9.031009
[22] М. Шинишевский, А. Ромито и Х. Шомерус, «Переход зацепления при слабых измерениях переменной силы», Phys.Ред. B 100, 064204 (2019).
https: / / doi.org/ 10.1103 / PhysRevB.100.064204
[23] Сунвон Чой, Иму Бао, Сяо-Лян Ци и Эхуд Альтман, «Квантовая коррекция ошибок в динамике скремблирования и вызванная измерениями Фазовый переход » Phys. Rev. Lett. 125, 030505 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.030505
[24] Чао-Мин Цзянь, И-Чжуан Ю, Ромен Вассер и Андреас В.В. Людвиг, схемы » Phys.Ред. B 101, 104302 (2020).
https: / / doi.org/ 10.1103 / PhysRevB.101.104302
[25] Кшек Туркеши, Розарио Фацио и Марчелло Дальмонте, «Критичность, индуцированная измерениями в $ (2 + 1) $ — мерном гибриде. квантовые схемы » Phys. Ред. B 102, 014315 (2020).
https: / / doi.org/ 10.1103 / PhysRevB.102.014315
[26] Д. Бернар, Т. Джин, О. Шпильберг, «Транспорт в квантовых цепях под строгим контролем» EPL (Europhysics Письма) 121, 60006 (2018).
https: // doi.org / 10.1209 / 0295-5075 / 121/60006
[27] Сяню Цао, Антуан Тиллой и Андреа Де Лука, «Запутанность в фермионной цепочке при постоянном мониторинге» SciPost Phys. 7, 24 (2019).
https: / / doi.org/ 10.21468 / SciPostPhys.7.2.024
[28] Д.А. Иванов, Т.Ю. Иванова, С.Ф. Кабальеро-Бенитес, И.Б. Мехов, « Квантовые фазовые переходы с обратной связью с использованием слабых измерений » Phys. Rev. Lett. 124, 010603 (2020).
https: // doi.org/ 10.1103 / PhysRevLett.124.010603
[29] Дау Ян, Андрей Гранкин, Лукас М. Зиберер, Денис В. Васильев и Петер Золлер, «Квантовое неразрушающее измерение гамильтониана многих тел» Nature Communications 11, 775 (2020).
https: / / doi.org/ 10.1038 / s41467-020-14489-5
[30] Йохей Фуджи и Юто Ашида «Квантовая критичность, вызванная измерениями при непрерывном мониторинге», Phys. Ред. B 102, 054302 (2020).
https: / / doi.org/ 10.1103 / PhysRevB.102.054302
[31] Юто Ашида, Цзунпин Гонг и Масахито Уэда, «Неэрмитская физика» (2020).
https: / / doi.org/ 10.1080 / 00018732.2021.1876991
[32] Тони Э. Ли и Чинг-Кит Чан «Предвестник магнетизма в неэрмитовых атомных системах» Phys. Ред. X 4, 041001 (2014).
https: / / doi.org/ 10.1103 / PhysRevX.4.041001
[33] Р. Х. Дикке «Когерентность в процессах спонтанного излучения» Phys. Ред. 93, 99–110 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99
[34] М. Гроссанд С. Гарош «Сверхизлучение: очерк теории коллективного спонтанного излучения» Physics Reports 93, 301 — 396 (1982).
https: / / doi.org/ 10.1016 / 0370-1573 (82)
-8
http: / / www.sciencedirect.com/ science / article / pii / 0370157382
8
[35] GL Celardoand L. Kaplan «Переход сверхизлучения в одномерных наноструктурах: эффективный неэрмитов гамильтонов формализм» Phys. Ред. B 79, 155108 (2009).
https: / / doi.org/ 10.1103 / PhysRevB.79.155108
[36] Нафтали Ауэрбаханд Владимир Зелевинский «Сверхизлучательная динамика, дверные проемы и резонансы в ядрах и других открытых мезоскопических системах» Отчеты о прогрессе в Физика 74, 106301 (2011).
https: / / doi.org/ 10.1088 / 0034-4885 / 74/10/106301
[37] А. Бьелла, Ф. Боргонови, Р. Кайзер и Г.Л. Селардо, « Субизлучательные гибридные состояния в открытой трехмерной модели Андерсона-Дике » EPL (Europhysics Letters) 103, 57009 (2013).
https: / / doi.org/ 10.1209 / 0295-5075 / 103/57009
[38] Уильям Герин, Мишель О. Араужо и Робин Кайзер, «Субизлучение в большом облаке холода. Атомы ‘Phys. Rev. Lett. 116, 083601 (2016).
https: // doi.org/ 10.1103 / PhysRevLett.116.083601
[39] И. Роттеран и Дж. П. Берд. «Обзор прогресса в физике открытых квантовых систем: теория и эксперимент», Reports on Progress in Physics 78, 114001 (2015).
https: / / doi.org/ 10.1088 / 0034-4885 / 78/11/114001
[40] Адам Нахум, Стхитадхи Рой, Брайан Скиннер и Джонатан Рухман, «Измерение и запутывание. Фазовые переходы в универсальных квантовых схемах, на квантовых деревьях и в теории Ландау-Гинзбурга » PRX Quantum 2, 010352 (2021).
https: // doi.org. Phys. Ред. B 103, 224210 (2021 г.).
Phys. Ред. B 103, 224210 (2021 г.).
https: / / doi.org/ 10.1103 / PhysRevB.103.224210
[42] О. Альбертон, М. Буххольд, С. Диль, «Переход запутанности в контролируемой цепочке свободных фермионов: от расширенного Критичность к закону области // Phys.3} $ Теория поля ‘Phys. Rev. Lett. 40, 1610 — 1613 (1978).
https: / / doi.org/ 10.1103 / PhysRevLett.40.1610
[44] Джон Л. Карди «Конформная инвариантность и краевая сингулярность Янга-Ли в двух измерениях» Phys. Rev. Lett. 54, 1354–1356 (1985).
https: / / doi.org/ 10.1103 / PhysRevLett.54.1354
[45] Джеймс М. Хики, Сэм Генуэй, Игорь Лесановский и Хуан П. Гаррахан, «Интегрированные во времени наблюдаемые как параметры порядка для переходы полной статистики счета в замкнутых квантовых системах // Phys.Ред. B 87, 184303 (2013).
https: / / doi.org/ 10.1103 / PhysRevB.87.184303
[46] Карл М. Бендер «PT-симметричная квантовая теория», Журнал Физики: Серия конференций 631, 012002 (2015).
https: / / doi. org/ 10.1088 / 1742-6596 / 631/1/012002
org/ 10.1088 / 1742-6596 / 631/1/012002
[47] HP Breuerand F. Petruccione «Теория открытых квантовых систем» Oxford University Press (2002).
https: / / doi.org/ 10.1093 / acprof: oso / 9780199213900.001.0001
[48] А.Б. Харрис «Верхние границы температур перехода обобщенных моделей Изинга» Journal of Physics C: Solid Государственная физика 7, 3082–3102 (1974).
https: / / doi.org/ 10.1088 / 0022-3719 / 7/17/018
[49] RB Stinchcombe «Разбавленная квантовая поперечная модель Изинга», Journal of Physics C: Solid State Physics 14, L263 – L267 (1981).
https: / / doi.org/ 10.1088 / 0022-3719 / 14/10/003
[50] Фостер Томпсон и Раджив Р.П. Сингх « Особенности Гриффитса-МакКоя в разреженном поперечном поле Изинга модель: численное исследование связанного расширения кластера » Phys. Ред. E 99, 032129 (2019).
https: // doi.org/ 10.1103 / PhysRevE.99.032129
[51] Т. Сентиленд Субир Сачдев «Реализации активированного динамического масштабирования в более высоких измерениях при случайных квантовых переходах» Phys. Rev. Lett. 77, 5292–5295 (1996).
Rev. Lett. 77, 5292–5295 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.5292
[1] Шао-Кай Цзянь, Чжи-Ченг Ян, Чжэнь Би и Сяо Чен, «Краевая сингулярность Ян-Ли вызвала переход запутанности» , arXiv: 2101.04115, Physical Review B 104 16, L161107 (2021).
[2] Тяньци Чжоу и Сяо Чен, «Динамика неунитарной запутанности в системах с непрерывными переменными», Physical Review B 104 18, L180301 (2021).
[3] Давиде Россини и Этторе Викари, «Когерентная и диссипативная динамика при квантовых фазовых переходах», Physics Reports 936, 1 (2021).
[4] Грегори С. Бентсен, Субхайан Саху и Брайан Свингл, «Очистка, вызванная измерениями в больших объемах». N гибридные броуновские схемы », Physical Review B 104 9, 094304 (2021).
[5] Юто Ашида, Цзунпин Гонг и Масахито Уэда, «Неэрмитская физика», Успехи в физике 69 3, 249 (2020).
[6] М. Буххольд, Ю. Миногучи, А.Альтланд и С. Дил, «Эффективная теория индуцированного измерениями фазового перехода фермионов Дирака», Physical Review X 11 4, 041004 (2021).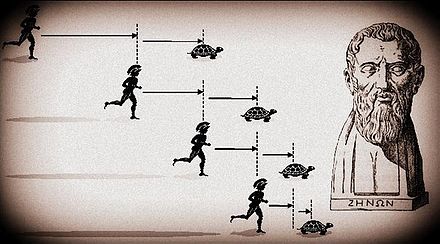
[7] Саранг Гопалакришнан и Майкл Дж. Гулланс, «Запутанность и очищающие переходы в неэрмитовой квантовой механике», Physical Review Letters 126 17, 170503 (2021).
[8] Кшек Туркеши, Альберто Бьелла, Розарио Фацио, Марчелло Дальмонте и Марко Скиро, «Индуцированные измерениями переходы запутанности в квантовой цепочке Изинга: от бесконечных к нулевым щелчкам», Physical Review B 103 22, 224210 (2021).
[9] Шао-Кай Цзянь, Чуньсяо Лю, Сяо Чен, Брайан Свингл и Пэнфэй Чжан, «Фазовый переход, вызванный измерениями в контролируемой модели Сачдэва-Е-Китаева», Physical Review Letters 127 14, 140601 (2021).
[10] Джек Туркеши, «Критичность, вызванная измерениями, как переход структуры данных», arXiv: 2101.06245.
[11] Петр Сирант, Джулиано Кириако, Федерика М. Сураче, Шраддха Шарма, Кшек Туркеши, Марчелло Дальмонте, Розарио Фацио и Гвидо Пагано, «Диссипативная динамика флоке: от устойчивого состояния к критичности, обусловленной измерениями в цепях захваченных ионов», arXiv: 2107. 05669.
05669.
[12] Элмер В. Х. Догген, Юваль Гефен, Игорь В. Горный, Александр Д. Мирлин и Дмитрий Г. Поляков, «Обобщенные квантовые измерения с матричным произведением состояний: фазовый переход сцепления и кластеризация», arXiv: 2104.10451.
[13] Т. Бурман, М. Шинишевский, Х. Шомерус и А. Ромито, «Диагностика динамики запутанности в зашумленных и неупорядоченных спиновых цепочках с помощью индуцированного измерениями стационарного перехода запутанности», arXiv: 2107.11354.
[14] Петр Сирант и Хек Туркеши, «Универсальное поведение за пределами мультифрактальности волновых функций при фазовых переходах, вызванных измерением», arXiv: 2109.06882.
[15] Кевин Т. Гейер и Филипп Хауке, «От неэрмитовой линейной реакции к динамическим корреляциям и флуктуационно-диссипативным соотношениям в квантовых системах многих тел», arXiv: 2104.03983.
[16] Цзи Цзоу, Шу Чжан и Ярослав Церковняк, «Генерация состояния Белла для спиновых кубитов посредством диссипативной связи», arXiv: 2108. 07365.
07365.
[17] Абхиджит П. Чаудхари, Шейн П. Келли, Риккардо Хавьер Валенсия Тортора и Джамир Марино, «Кроссоверы Зенона в скорости запутывания спиновых цепочек с шумными примесями», arXiv: 2103.16172.
[18] Санкхья Басу, Даниэль П. Аровас, Саранг Гопалакришнан, Крис А. Хули и Вадим Оганесян, «Нули Фишера и постоянные временные колебания в неунитарных квантовых схемах», arXiv: 2103.10628.
[19] Грэхем Келлс, Дганит Мейдан и Алессандро Ромито, «Топологические переходы с непрерывно контролируемыми свободными фермионами», arXiv: 2112.09787.
Вышеупомянутые цитаты взяты из цитируемой службы Crossref (последнее обновление успешно 2021-12-27 15:44:17) и SAO / NASA ADS (последнее успешное обновление 2021-12-27 15:44:18).Список может быть неполным, поскольку не все издатели предоставляют подходящие и полные данные о цитировании.
Уайтхед на Зеноне
Уайтхед на Зеноне От Альфреда Норта Уайтхеда
Процесс и реальность
Часть II, Глава II, Раздел II
(Macmillan 1929, стр.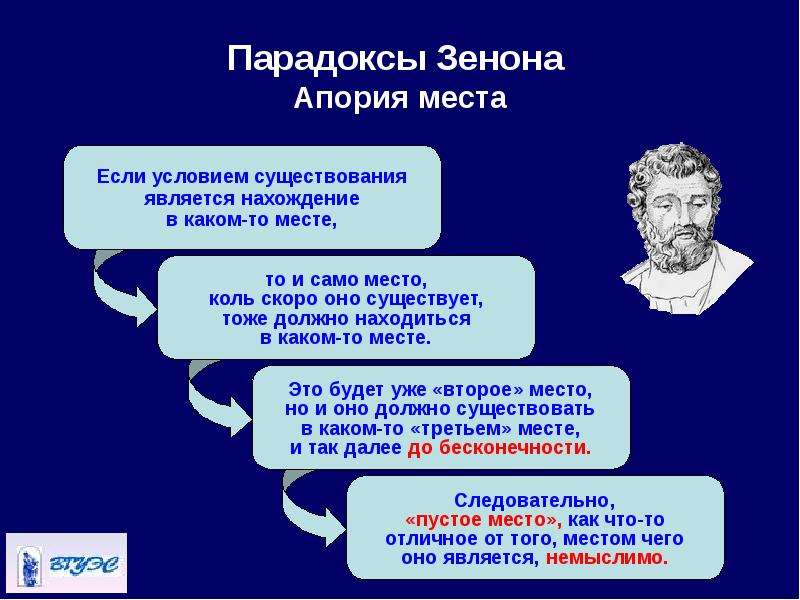 104-107)
104-107)
Реальные сущности распыляют обширный континуум. Этот континуум
сам по себе является просто возможностью разделения;
это подразделение осуществляет фактическая организация. Объективация
современного мира просто выражает этот мир
с точки зрения его потенциальной возможности для подразделения и с точки зрения
взаимных перспектив, которые любое такое подразделение
приведет к реальной эффективности.Это первичные управляющие данные
для любой реальной организации; поскольку они выражают
, как все реальные сущности находятся в едином мире.
С появлением любой реальной сущности то, что
ранее было потенциальным в пространственно-временном континууме, теперь
является первичной реальной фазой чего-то актуального. Для каждого
процесса конкресенции была принята
региональная мировая точка зрения,
определяющая ограниченную возможность объективации. В простом обширном континууме
нет принципа для определения того, какие региональные кванты должны быть атомизированы
, чтобы сформировать реальную перспективную точку зрения
для первичных данных, составляющих базовую фазу в конкресценции
реальной сущности. Факторы
Факторы
реального мира, посредством которых осуществляется это определение, будут обсуждены на более поздней стадии исследования. Они
составляют начальную фазу «субъективной цели». Эта начальная фаза
является прямым производным от изначальной природы Бога
. В этой функции, как и в любой другой, Бог —
орган новизны, направленный на усиление.
В простом континууме есть противоположные возможности; в реальном мире существуют определенные атомарные реальности, определяющие одну связную систему реальных делений во всей области действительности.Каждая действительная сущность
в ее отношении к другим реальным сущностям находится в этом смысле
где-то в континууме и возникает из
данных, предоставляемых этой точкой зрения. Но в другом смысле
он присутствует повсюду в континууме; поскольку его состав
включает объективации реального мира
и, таким образом, включает континуум; также
РАСШИРЕННЫЙ КОНТИНУУМ 106
потенциальных объективации самих себя способствуют
реальных потенциальных возможностей, солидарность которых выражает континуум.
Таким образом, континуум присутствует в каждой реальной сущности, и
каждая реальная сущность пронизывает континуум.
Этот вывод можно сформулировать иначе. Расширение
, помимо его пространственной и временной привязки, представляет собой общую схему
отношений, обеспечивающую способность
, что многие объекты могут быть объединены в реальное единство
одного опыта. Таким образом, акт опыта имеет объективную схему экстенсивного порядка из-за двойного
факта, что его собственная точка зрения имеет обширное содержание
и что другие фактические сущности объективированы
с сохранением их обширных отношений.Эти обширные отношения
более фундаментальны, чем их более специальные пространственные и временные отношения
. Расширение — это наиболее общая схема реальной потенциальности, служащая фоном для всех других органических отношений.
Потенциальная схема не определяет собственной атомизации
реальными сущностями. Он делимый; но его реальное деление на фактические сущности зависит от более конкретных характеристик
фактических сущностей, составляющих предшествующую среду. Что касается времени, эта атомизация
Что касается времени, эта атомизация
принимает особую форму «эпохальной теории времени».
В отношении пространства это означает, что
каждой действительной сущности во временном мире следует приписать пространственный объем
с точки зрения перспективы. Эти выводы
требуются при рассмотрении аргументов Зенона в
связи с предположением, что реальная сущность — это акт опыта
. В подтверждение этого вывода можно привести авторитет Уильяма Джеймса
.Он пишет:
«Либо ваш опыт не имеет содержания, без изменений, либо
это ощутимое количество содержания или изменений. может
разделить их на компоненты, но, как сразу указано,
2 Ср. мой Наука
и современный мир, гл. VII.
8 Ср. loc. соч. и Часть IV настоящей работы.
106 ПРОЦЕСС И РЕАЛЬНОСТЬ
приходят полностью или не приходят совсем.»* Джеймс
также относится к
Zeno. По сути, я согласен с его аргументом Зенона;
, хотя я не думаю, что он допускает в достаточной мере те
элементы в парадоксах Зенона, которые являются продуктом
неадекватных математических знаний. Но я согласен с тем, что
Но я согласен с тем, что
действительный аргумент остается после удаления недействительных частей
.
Аргумент, поскольку он действителен, вызывает
противоречие с двумя предпосылками: (i) что в становлении что-то (res vera) становится, и (ii) что каждый акт
становления делится на более ранние и последующие части, которые
сами являются действиями становления.Рассмотрим, например,
как акт становления в течение одной секунды. Действие
делится на два действия: одно — в первой половине второго,
— второе — во второй половине второго. Таким образом,
, который становится в течение всего второго, предполагает тот
, который становится в течение первой полсекунды. Аналогично,
то, что становится в течение первой полусекунды presup-
, представляет собой то, что становится в течение первой четверти секунды,
и так далее до бесконечности. Таким образом, если мы рассмотрим процесс становления
до начала секунды, о которой идет речь,
и спросим, что тогда становится, мы не сможем дать никакого ответа. Ведь
любое существо, которое мы указываем, предполагает более раннее существо
, которое стало после начала второго
и предшествовало более раннему существу. Следовательно,
— это не то, что становится, чтобы осуществить переход в
второй рассматриваемый.
Трудность не обойдется, если предположить, что
что-то
становится в каждый непродолжительный момент времени. Ибо у
начало секунды времени нет следующего момента
, в который что-то могло бы случиться.
Зенон в своей «Стреле в полете», кажется,
смутно уловил этот аргумент. Но введение движения
вносит несущественные детали. Истинная трудность
— понять, как стрела выживает с течением времени.
* Ср. Некоторые проблемы философии, Cf. ИКС; мой
Внимание было привлечено
к этому отрывку из-за его цитаты в Religion in The Philosophy of
William James, профессора Дж. С. Бикслера.
РАСШИРЕННЫЙ КОНТИНУУМ 107
К сожалению, трактовка «выносливости» Декартом
очень поверхностен, и последующие философы
последовали его примеру.
В своем «Ахиллесе и черепахе» Зенон приводит
неверный аргумент, зависящий от незнания теории
бесконечных сходящихся числовых рядов. Исключая
нерелевантных деталей расы и движения — подробностей, которые
сделали парадоксом для литературы всех возрастов —
рассматривает первую полсекунду как один акт становления,
следующую четверть секунды как еще один такой акт, следующая восьмая —
секунда как еще одна, и так до бесконечности.Затем Зенон,
, незаконно предполагает, что эта бесконечная серия актов становления никогда не может быть исчерпана. Но нет необходимости
предполагать, что бесконечная серия актов становления, с
первым действием, и каждое действие с непосредственным последующим действием,
неисчерпаемо в процессе становления. Простая арифметика — метика
уверяет нас, что только что указанный ряд будет исчерпан за одну секунду. Тогда открывается путь
для вмешательства нового акта становления, который
лежит за пределами всей серии. Таким образом, этот парадокс Зенона
Таким образом, этот парадокс Зенона
основан на математической ошибке.
Модификация парадокса «Стрелка», изложенная выше,
выявляет принцип, что каждый акт становления должен иметь
непосредственного преемника, если мы допускаем, что что-то
становится. Ибо иначе мы не сможем указать, чем становится
существо, когда мы переходим ко второму рассматриваемому вопросу.
Но мы не можем, в отсутствие какой-либо дополнительной предпосылки,
сделать вывод, что у каждого акта становления должен был быть непосредственный предшественник.
Вывод таков: в каждом акте становления
— становление чего-то с временным расширением; но
, что сам акт не является экстенсивным, в том смысле, что он
делится на более ранние и более поздние акты становления, которые
соответствуют обширной делимости того, что стало
.
Из тени и в топ-менеджмент: психическое здоровье и рабочее место
Когда-то доведенное до использования исключительно шепотом в коридоре подальше от босса, психическое здоровье стало одной из самых неотложных проблем для генеральных директоров и их руководителей, поскольку выросли более широкие движения, направленные на то, чтобы такие разговоры стали общепринятыми.
Хотя некоторые организации уже были на переднем крае психического здоровья и благополучия сотрудников до 2020 года, многочисленные события прошлого года, изменившие здоровье и общество, сделали психическое благополучие новым приоритетом на рабочем месте. Большинство из нас знает кого-то, кто напрямую пострадал от проблемы психического здоровья, такой как тревога, депрессия или самоубийство. А в прошлом году для многих было очевидно, что наши сотрудники испытывали эмоциональные трудности, как никогда раньше: были долгие темные дни пандемии, огромные новые обязанности по дому и волна социальных волнений, усиленных насилием.
Психическое здоровье также является последней проблемой на рабочем месте, с которой сталкиваются руководители по связям с общественностью (CCO), которые в течение многих лет находились на переднем крае разработки внутренних и внешних подходов к множеству сложных тем, влияющих на моральный дух и производительность сотрудников, таких как сексуальное насилие. домогательства, расовое и гендерное неравенство, социальная справедливость, DE + I и политика. Теперь CCO и руководители агентств сталкиваются с еще одной деликатной и глубоко личной проблемой на пересечении бизнес-реалий и социальных реалий.
домогательства, расовое и гендерное неравенство, социальная справедливость, DE + I и политика. Теперь CCO и руководители агентств сталкиваются с еще одной деликатной и глубоко личной проблемой на пересечении бизнес-реалий и социальных реалий.
Согласно недавнему опросу CCO, проведенному в рамках весеннего семинара Общества Пейдж на тему «Устойчивость в эпоху повсеместных изменений», почти все признают, что открытый разговор о психическом здоровье на рабочем месте чрезвычайно важен. Напротив, только 26% опрошенных считают, что их компания «делает все возможное» для решения этой проблемы. Отвечая на вопрос о роли генерального директора, 85% ответили, что для генерального директора очень важно уделять особое внимание психическому здоровью и благополучию сотрудников , , в то время как менее трех четвертей (74%) ответили, что их генеральный директор в настоящее время уделяет приоритетное внимание психическому здоровью и благополучию сотрудников. .
Очевидно, что мы все еще находимся на ранних этапах нормализации разговоров о психическом здоровье на рабочем месте. Только 4 из 10 опрошенных CCO заявили, что получают большую поддержку, рекомендации и ресурсы для решения проблем психического здоровья и благополучия, а 67% заявили, что одной из самых больших проблем в развитии открытого диалога является «беспокойство сотрудников по поводу суждений». и потенциальное негативное влияние на их карьеру. «Наиболее важными ресурсами, определенными CCO для эффективного решения вопросов психического здоровья, являются: полное участие высшего руководства (33%), специальный консультант по медицинскому / психическому здоровью, который поможет с надлежащим язык (22%) и ресурсы аккредитованной психиатрической организации.Также были отмечены место, куда можно направить людей для получения информации, и обучение ведению деликатных разговоров.
Только 4 из 10 опрошенных CCO заявили, что получают большую поддержку, рекомендации и ресурсы для решения проблем психического здоровья и благополучия, а 67% заявили, что одной из самых больших проблем в развитии открытого диалога является «беспокойство сотрудников по поводу суждений». и потенциальное негативное влияние на их карьеру. «Наиболее важными ресурсами, определенными CCO для эффективного решения вопросов психического здоровья, являются: полное участие высшего руководства (33%), специальный консультант по медицинскому / психическому здоровью, который поможет с надлежащим язык (22%) и ресурсы аккредитованной психиатрической организации.Также были отмечены место, куда можно направить людей для получения информации, и обучение ведению деликатных разговоров.
Хотя 2020 год — это год, о котором многие из нас хотели бы забыть, он подчеркивает — и это соответствует растущему вниманию к психическому благополучию — что еще долго после того, как пандемия уйдет, наши сотрудники и заинтересованные стороны будут помнить, как мы это делали ( или нет) ведет с состраданием. И они никогда не забудут, как мы заставили их почувствовать себя своими действиями и усилиями, которые мы приложили, чтобы понять, как они справляются.Этот опыт также научил нас многому о том, кто мы есть и что важно, и что значит заботиться о людях, находящихся в нашем ведении. Сотрудники, особенно молодое поколение, ожидают, что работодатели будут заботиться о них как о людях и обо всем остальном. У них было такое ожидание даже до 2020 года, и так оно и останется.
И они никогда не забудут, как мы заставили их почувствовать себя своими действиями и усилиями, которые мы приложили, чтобы понять, как они справляются.Этот опыт также научил нас многому о том, кто мы есть и что важно, и что значит заботиться о людях, находящихся в нашем ведении. Сотрудники, особенно молодое поколение, ожидают, что работодатели будут заботиться о них как о людях и обо всем остальном. У них было такое ожидание даже до 2020 года, и так оно и останется.
Как хранители корпоративной репутации и голос совести в компании , CCO занимают уникальное положение, чтобы гарантировать, что мы не упустим из виду необходимость более открытого и прямого диалога по вопросам психического здоровья и благополучия.Я надеюсь, что человеческая доброта, свидетелями которой мы стали во время пандемии, останется прочной и мощной силой на рабочем месте для нас самих и для тех, кто полагается на нас в правильных поступках.
зеноновых точек в моделях оптимального управления с переключением эндогенного режима
Автор
Abstract
В данной статье рассматривается тип многоступенчатой задачи, в которой лицо, принимающее решение, может оптимальным образом решить переключиться между двумя чередующимися этапами (режимами).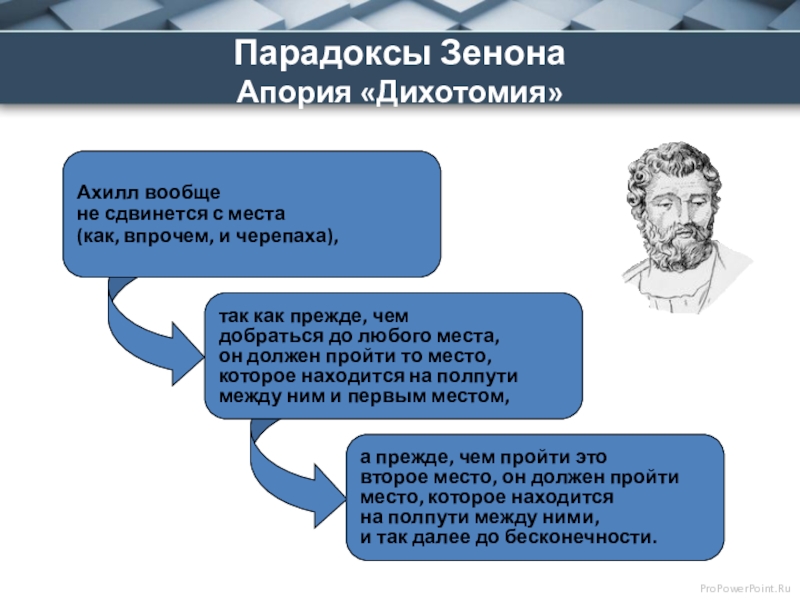 В такой задаче либо одна из двух стадий доминирует в долгосрочной перспективе, либо оптимально бесконечно переключаться между стадиями. Точка, в которой такое явление происходит с оптимальным нулевым временем переключения, называется точкой Зенона.
В такой задаче либо одна из двух стадий доминирует в долгосрочной перспективе, либо оптимально бесконечно переключаться между стадиями. Точка, в которой такое явление происходит с оптимальным нулевым временем переключения, называется точкой Зенона.
Рекомендуемая ссылка
DOI: 10.1016 / j.jedc.2018.09.010
Скачать полный текст от издателя
Поскольку доступ к этому документу ограничен, вы можете поискать его другую версию.
Ссылки на IDEAS
- Boucekkine, R. & Pommeret, A. & Prieur, F., 2013.
« Оптимальное переключение режимов и пороговые эффекты ,»
Журнал экономической динамики и управления, Elsevier, vol. 37 (12), страницы 2979-2997.
- Boucekkine, Raouf & Saglam, Cagri & Valléee, Thomas, 2004.«Внедрение технологии в стадии реализации: двухэтапный подход к оптимальному управлению »,
Макроэкономическая динамика, Cambridge University Press, vol. 8 (2), страницы 250-271, апрель.
- Рауф Бусеккин, Кагри Саглам и Томас Валле, 1999. «Внедрение технологии в стадии реализации: двухэтапный подход к оптимальному управлению », Пост-печать хал-03193663, HAL.
- BOUCEKKINE, Raouf & SAGLAM, Cagri & VALLEE, Thomas, 2004. « Внедрение технологии в соответствии с воплощением: двухэтапный подход оптимального управления », LIDAM перепечатывает CORE 1702 г., Католический университет Лувена, Центр исследований операций и эконометрики (CORE).
- BOUCEKKINE, RAOUF & SAGLAM, Cagri & VALLÉE, Thomas, 2003.
« Внедрение технологии в соответствии с воплощением: двухэтапный подход оптимального управления »,
Документы для обсуждения LIDAM CORE
2003055, Католический университет Лувена, Центр исследований операций и эконометрики (CORE).

- Raouf, BOUCEKKINE & Cagri, SAGLAM & Thomas, VALLEE, 2002. « Принятие технологии в соответствии с вариантом воплощения: двухэтапный подход оптимального управления », Документы для обсуждения LIDAM IRES 2003007, Католический университет Лувена, Институт экономических и социальных исследований (IRES).
- Long, Ngo Van & Prieur, Fabien & Tidball, Mabel & Puzon, Klarizze, 2017. « Кусочно-замкнутые равновесия в дифференциальных играх со стратегиями переключения режимов ,» Журнал экономической динамики и управления, Elsevier, vol. 76 (C), страницы 264-284.
- Мишель, Филипп, 1982. « Об условии трансверсальности в оптимальных задачах бесконечного горизонта «, Econometrica, Econometric Society, vol. 50 (4), страницы 975-985, июль.
- Колкинс, Джонатан П.И Файхтингер, Густав и Грасс, Дитер и Хартл, Ричард Ф. и Корт, Питер М. и Зейдл, Андреа, 2013.
« Когда делать проприетарное программное обеспечение с открытым исходным кодом »,
Журнал экономической динамики и управления, Elsevier, vol.
 37 (6), страницы 1182-1194.
37 (6), страницы 1182-1194. - Томияма, Кен, 1985. « Двухэтапные задачи оптимального управления и условия оптимальности ,» Журнал экономической динамики и управления, Elsevier, vol. 9 (3), страницы 317-337, ноябрь.
- Эльке Мозер, Андреа Зайдл и Густав Файхтингер, 2014 г.« Зависимость от истории в моделях компромисса между производством и загрязнением: многоступенчатый подход », Анналы исследований операций, Springer, vol. 222 (1), страницы 457-481, ноябрь.
- Рейнольдс, Стэнли С., 1987. « Инвестиции в мощности, упреждение и обязательства в модели Infinite Horizon », Международное экономическое обозрение, Департамент экономики, Пенсильванский университет и Институт социальных и экономических исследований Университета Осаки, т. 28 (1), страницы 69-88, февраль.
- Дитер Грасс, Ричард Ф. Хартл и Питер М. Корт, 2012 г.
«Накопление капитала и технологический прогресс »,
Журнал теории оптимизации и приложений, Springer, vol. 154 (2), страницы 588-614, август.
- Томияма, Кен и Россана, Роберт Дж., 1989. « Двухэтапные задачи оптимального управления с явной зависимостью от точки переключения: критерии оптимальности и пример задержек поставки и инвестиций ,» Журнал экономической динамики и управления, Elsevier, vol.13 (3), страницы 319-337, июль.
- Дмитрий Громов и Екатерина Громова, 2017. « об одном классе гибридных дифференциальных игр », Динамические игры и приложения, Springer, vol. 7 (2), страницы 266-288, июнь.
- Зайдл, Андреа и Колкинс, Джонатан П. и Хартл, Ричард Ф. и Корт, Питер М., 2018. « Серьезная стратегия для создателей развлечений: анализ возможности перехода от платной игры к бесплатной в двухэтапной модели оптимального управления с квадратичными затратами », Европейский журнал операционных исследований, Elsevier, vol.267 (2), страницы 700-715.
- Хартл, Ричард Ф., 1987.
« Простое доказательство монотонности траекторий состояний в задачах автономного управления ,»
Журнал экономической теории, Elsevier, vol.
 41 (1), страницы 211-215, февраль.
41 (1), страницы 211-215, февраль. - Колкинс, Джонатан П. и Файхтингер, Густав и Грасс, Дитер и Хартл, Ричард Ф. и Корт, Питер М. и Зейдл, Андреа, 2015. « очков Скибы в бесплатных задачах конца времени », Журнал экономической динамики и управления, Elsevier, vol.51 (C), страницы 404-419.
- Макрис, Милтиадис, 2001. « Необходимые условия для бесконечного горизонта дисконтированных двухэтапных задач оптимального управления ,» Журнал экономической динамики и управления, Elsevier, vol. 25 (12), страницы 1935-1950, декабрь.
- Корт, Питер М. и Врзачек, Стефан, 2015. « Оптимальный рост фирмы под угрозой входа на рынок », Европейский журнал операционных исследований, Elsevier, vol. 246 (1), страницы 281-292.
Самые популярные товары
Это элементы, которые чаще всего цитируют те же работы, что и эта, и цитируются в тех же работах, что и эта.
- Зайдл, Андреа и Колкинс, Джонатан П. и Хартл, Ричард Ф. и Корт, Питер М., 2018. « Серьезная стратегия для создателей развлечений: анализ возможности перехода от платной игры к бесплатной в двухэтапной модели оптимального управления с квадратичными затратами », Европейский журнал операционных исследований, Elsevier, vol. 267 (2), страницы 700-715.
- Эльке Мозер, Андреа Зайдл и Густав Файхтингер, 2014 г. « Зависимость от истории в моделях компромисса между производством и загрязнением: многоступенчатый подход », Анналы исследований операций, Springer, vol.222 (1), страницы 457-481, ноябрь.
- Стефан Врзачек, Майкл Кун и Иван Франкович, 2020. « Использование возрастной структуры для многоступенчатой модели оптимального управления со случайным временем переключения », Журнал теории оптимизации и приложений, Springer, vol. 184 (3), страницы 1065-1082, март.
- Нго Ван Лонг, Фабьен Приер, Клариц Пузон и Мэйбл Тидбол, 2013 г.
« Марковские совершенные равновесия в дифференциальных играх со стратегиями переключения режимов »,
Рабочие бумаги
13-06, LAMETA, Университет Монпелье, отредактировано в январе 2014 г.

- Доган, Эрол и Ле Ван, Куонг и Саглам, Кагри, 2011.
« Оптимальное время переключения режимов в моделях оптимального роста: подход Соболева «,
Математические социальные науки, Elsevier, vol. 61 (2), страницы 97-103, март.
- Эрол Доган и Куонг Ле Ван и Кагри Саглам, 2010 г. « Оптимальное время переключения режимов в моделях оптимального роста: подход Соболева «, Рабочие бумаги 16, Центр исследований развития и политики (DEPOCEN), Вьетнам.
- Куонг Ле Ван, Эрол Доган и Кэгри Саглам, 2011 г. « Оптимальное время переключения режимов в моделях оптимального роста: подход Соболева «, PSE-Ecole d’économie de Paris (Постпринт) halshs-00639729, HAL.
- Куонг Ле Ван, Эрол Доган и Кэгри Саглам, 2011 г. « Оптимальное время переключения режимов в моделях оптимального роста: подход Соболева «, Université Paris1 Panthéon-Sorbonne (послепечатные и рабочие документы) halshs-00639729, HAL.
- Рауф Бусеккин, Кармен Камачо и Бентенг Зу, 2020.
 « Оптимальный переход от конкуренции к сотрудничеству: предварительная разведка ,»
Рабочие бумаги
halshs-02434786, HAL.
« Оптимальный переход от конкуренции к сотрудничеству: предварительная разведка ,»
Рабочие бумаги
halshs-02434786, HAL.- Рауф Бусеккин, Кармен Камачо и Бентенг Зу, 2020. « Оптимальный переход от конкуренции к сотрудничеству: предварительная разведка ,» Рабочие документы PSE halshs-02434786, HAL.
- Рауф Бусеккин, Кармен Камачо и Бентенг Зу, 2020.« Оптимальный переход от конкуренции к сотрудничеству: предварительная разведка ,» Серия дискуссионных документов DEM 20-02, факультет экономики Люксембургского университета.
- Рауф Бусеккин, Кармен Камачо и Бентенг Зу, 2021 год. « Оптимальный переход от конкуренции к сотрудничеству: предварительная разведка ,» PSE-Ecole d’économie de Paris (Постпринт) хал-02950698, HAL.
- Рауф Бусеккин, Кармен Камачо и Бентенг Зу, 2021 год.« Оптимальный переход от конкуренции к сотрудничеству: предварительная разведка ,» Пост-печать хал-02950698, HAL.
- Boucekkine, R.
 & Pommeret, A. & Prieur, F., 2013.
« Оптимальное переключение режимов и пороговые эффекты ,»
Журнал экономической динамики и управления, Elsevier, vol. 37 (12), страницы 2979-2997.
& Pommeret, A. & Prieur, F., 2013.
« Оптимальное переключение режимов и пороговые эффекты ,»
Журнал экономической динамики и управления, Elsevier, vol. 37 (12), страницы 2979-2997. - Behringer, Stefan & Upmann, Thorsten, 2017. « Получение удаленного возобновляемого ресурса », Ежегодная конференция VfS 2017 (Вена): Альтернативные структуры для денег и банковского дела 168250, Verein für Socialpolitik / Немецкая экономическая ассоциация.
- Дитер Грасс, Ричард Ф. Хартл и Питер М. Корт, 2012 г. «Накопление капитала и технологический прогресс », Журнал теории оптимизации и приложений, Springer, vol. 154 (2), страницы 588-614, август.
- Long, Ngo Van & Prieur, Fabien & Tidball, Mabel & Puzon, Klarizze, 2017. « Кусочно-замкнутые равновесия в дифференциальных играх со стратегиями переключения режимов ,» Журнал экономической динамики и управления, Elsevier, vol.76 (C), страницы 264-284.
- Raouf Boucekkine & Aude Pommeret & Fabien Prieur, 2013 г.
 « О сроках и оптимальности контроля за капиталом: государственные расходы, динамика долга и благосостояние »,
Международный журнал экономической теории, Международное общество экономической теории, вып. 9 (1), страницы 101-112, март.
« О сроках и оптимальности контроля за капиталом: государственные расходы, динамика долга и благосостояние »,
Международный журнал экономической теории, Международное общество экономической теории, вып. 9 (1), страницы 101-112, март.- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г. « О сроках и оптимальности контроля за капиталом: государственные расходы, динамика долга и благосостояние », Cahiers de Recherches Economiques du Département d’économie 12.01, Университет Лозанны, Факультет HEC, Департамент экономики.
- Raouf Boucekkine & Aude Pommeret & Fabien Prieur, 2013 г. « О сроках и оптимальности контроля за капиталом: государственные расходы, динамика долга и благосостояние », Пост-печать hal-01498252, HAL.
- Raouf Boucekkine & Aude Pommeret & Fabien Prieur, 2013 г. « О сроках и оптимальности контроля за капиталом: государственные расходы, динамика долга и благосостояние », Пост-печать хал-01549828, HAL.
- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г.
 « О сроках и оптимальности контроля над капиталом. Государственные расходы, динамика долга и благосостояние «,
Рабочие документы AMSE
1212, Школа экономики Экс-Марсель, Франция.
« О сроках и оптимальности контроля над капиталом. Государственные расходы, динамика долга и благосостояние «,
Рабочие документы AMSE
1212, Школа экономики Экс-Марсель, Франция. - Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г. « О сроках и оптимальности контроля над капиталом: государственные расходы, динамика долга и благосостояние «, Рабочие бумаги halshs-00793196, HAL.
- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г.» О сроках и оптимальности контроля над капиталом: государственные расходы, динамика долга и благосостояние «, Рабочие бумаги 12-15, LAMETA, Университет Монпелье, отредактировано в мае 2012 г.
- Онори Дарья, 2015. « Оптимальный рост и динамика долга при обеспечении на основе ВВП », Рабочие бумаги halshs-01251352, HAL.
- Колкинс, Джонатан П. и Файхтингер, Густав и Грасс, Дитер и Хартл, Ричард Ф. и Корт, Питер М. и Зейдл, Андреа, 2013.« Когда делать проприетарное программное обеспечение с открытым исходным кодом »,
Журнал экономической динамики и управления, Elsevier, vol.
 37 (6), страницы 1182-1194.
37 (6), страницы 1182-1194. - Boucekkine, Raouf & Saglam, Cagri & Valléee, Thomas, 2004.
«Внедрение технологии в стадии реализации: двухэтапный подход к оптимальному управлению »,
Макроэкономическая динамика, Cambridge University Press, vol. 8 (2), страницы 250-271, апрель.
- Рауф Бусеккин, Кагри Саглам и Томас Валле, 1999. «Внедрение технологии в стадии реализации: двухэтапный подход к оптимальному управлению », Пост-печать хал-03193663, HAL.
- BOUCEKKINE, Raouf & SAGLAM, Cagri & VALLEE, Thomas, 2004. « Внедрение технологии в соответствии с воплощением: двухэтапный подход оптимального управления », LIDAM перепечатывает CORE 1702 г., Католический университет Лувена, Центр исследований операций и эконометрики (CORE).
- BOUCEKKINE, RAOUF & SAGLAM, Cagri & VALLÉE, Thomas, 2003.
« Внедрение технологии в соответствии с воплощением: двухэтапный подход оптимального управления »,
Документы для обсуждения LIDAM CORE
2003055, Католический университет Лувена, Центр исследований операций и эконометрики (CORE).

- Raouf, BOUCEKKINE & Cagri, SAGLAM & Thomas, VALLEE, 2002. « Принятие технологии в соответствии с вариантом воплощения: двухэтапный подход оптимального управления », Документы для обсуждения LIDAM IRES 2003007, Католический университет Лувена, Институт экономических и социальных исследований (IRES).
- Калиендо, Фрэнк Н. и Горри, Аспен и Славов, Сита, 2019. « Цена неуверенности в сроках реформы социального обеспечения », Европейский экономический обзор, Elsevier, т.118 (C), страницы 101-125.
- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г.
« Оптимальное переключение режима и пороговые эффекты: теория и приложение к проблеме извлечения ресурсов в условиях необратимости »,
Рабочие бумаги
halshs-00793200, HAL.
- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г.
« Оптимальное переключение режимов и пороговые эффекты. Теория и применение к проблеме извлечения ресурсов при необратимости »,
Рабочие документы AMSE
1213, Школа экономики Экс-Марсель, Франция.

- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г. « Оптимальное переключение режима и пороговые эффекты: теория и приложение к проблеме добычи ресурсов в условиях необратимости «, Cahiers de Recherches Economiques du Département d’économie 12 февраля, Университет Лозанны, Факультет HEC, Департамент экономики.
- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г. « Оптимальное переключение режима и пороговые эффекты: теория и приложение к проблеме извлечения ресурсов в условиях необратимости », Рабочие бумаги 12-14, LAMETA, Университет Монпелье, отредактировано в мае 2012 г.
- Raouf Boucekkine и Aude Pommeret & Fabien Prieur, 2012 г.
« Оптимальное переключение режимов и пороговые эффекты. Теория и применение к проблеме извлечения ресурсов при необратимости »,
Рабочие документы AMSE
1213, Школа экономики Экс-Марсель, Франция.
- Валле, Томас и Морено-Гальбис, Ева, 2011. « Оптимальное время переключения с тейлористической на целостную организацию рабочего места ,» Структурные изменения и экономическая динамика, Elsevier, vol. 22 (3), страницы 238-246, сентябрь.
- Энкарна Эстебан, Елена Кальво и Хосе Альбиак, 2021 год.
« Экосистемные сдвиги: последствия для управления подземными водами »,
Экономика окружающей среды и ресурсов, Springer; Европейская ассоциация экономистов-экологов и специалистов по ресурсам, т.
 79 (3), страницы 483-510, июль.
79 (3), страницы 483-510, июль. - Bonneuil, N. & Boucekkine, R., 2016.
« Оптимальный переход на возобновляемые источники энергии с порогом необратимого загрязнения ,»
Европейский журнал операционных исследований, Elsevier, vol. 248 (1), страницы 257-262.
- Ноэль Бонней и Рауф Бусеккин, 2014. « Оптимальный переход на возобновляемые источники энергии с порогом необратимого загрязнения », Рабочие документы AMSE 1434, Школа экономики Экс-Марсель, Франция, пересмотрена в августе 2014 г.
- Ноэль Бонней и Рауф Бусеккин, 2014. « Оптимальный переход на возобновляемые источники энергии с порогом необратимого загрязнения », Рабочие бумаги halshs-01025470, HAL.
- Ноэль Бонней и Рауф Бусеккин, 2016. « Оптимальный переход на возобновляемые источники энергии с порогом необратимого загрязнения ,» Пост-печать хал-01447849, HAL.
- Гезер, Серхат, 2019.
« Отложенное представление продукта: динамический анализ с эндогенным временным горизонтом »,
Журнал экономической динамики и управления, Elsevier, vol.
 102 (C), страницы 96-114.
102 (C), страницы 96-114.
Подробнее об этом товаре
Ключевые слова
Многоступенчатое моделирование; Точка Зенона; Переключение эндогенного режима;Все эти ключевые слова.
Классификация JEL:
- C61 — Математические и количественные методы — — Математические методы; Модели программирования; Математическое и имитационное моделирование — — — Оптимизационные методы; Модели программирования; Динамический анализ
- O33 — Экономическое развитие, инновации, технологические изменения и рост — — Инновации; Исследования и разработки; Технологические изменения; Права интеллектуальной собственности — — — Технологические изменения: выбор и последствия; Диффузионные процессы
Статистика
Доступ и загрузка статистикиИсправления
Все материалы на этом сайте предоставлены соответствующими издателями и авторами.Вы можете помочь исправить ошибки и упущения. При запросе исправления укажите дескриптор этого элемента: RePEc: eee: dyncon: v: 100: y: 2019: i: c: p: 353-368 . См. Общую информацию о том, как исправить материал в RePEc.
См. Общую информацию о том, как исправить материал в RePEc.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, заголовка, аннотации, библиографической информации или информации для загрузки, обращайтесь:. Общие контактные данные провайдера: http://www.elsevier.com/locate/jedc .
Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь.Это позволяет привязать ваш профиль к этому элементу. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которых мы не уверены.
Если CitEc распознал библиографическую ссылку, но не связал с ней элемент в RePEc, вы можете помочь с этой формой .
Если вам известно об отсутствующих элементах, цитирующих этот элемент, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылочного элемента. Если вы являетесь зарегистрированным автором этого элемента, вы также можете проверить вкладку «Цитаты» в своем профиле RePEc Author Service, поскольку там могут быть некоторые цитаты, ожидающие подтверждения.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, названия, аннотации, библиографической информации или информации для загрузки, обращайтесь: Catherine Liu (адрес электронной почты указан ниже). Общие контактные данные провайдера: http://www.elsevier.com/locate/jedc .
Обратите внимание, что исправления могут отфильтроваться через пару недель. различные сервисы RePEc.
Zeno | История кооператива
«Зенон Исаврианин» Тарасикодисса (умер в 491 г.)
Зенон был из Росумблада в провинции на юго-востоке Малой Азии, известной как Исаврия.
Император Лев призвал его в Константинополь в качестве лидера отряда исаврийцев, чтобы противостоять постоянно растущему влиянию Германии на империю. Также была создана особая имперская гвардия, полностью состоящая из исаврийцев, и Зенон получил командование этой очень важной силой.
Только на этом этапе он принял имя Зенон. Очевидно, это было имя высокопоставленного сановника в Исаврии, и Зенон считал, что для его нового высокого поста более уместно иметь менее распространенное имя, чем Тарасикодисса.
Чтобы еще больше укрепить связь со своими новыми исаврийскими гвардейцами, Лео женил свою старшую дочь Элию Ариадну на Зеноне. В 467-8 гг. Нашей эры Зенон получил влиятельную должность «магистра воинов» во Фракии, чтобы отразить нападение гуннов под командованием сына Аттилы, Денцига (Денсегиха).
Хотя Аспар, могущественный немецкий «военный командир» восточной империи, хорошо понимал Зенона как нового амбициозного противника и старался убрать его с дороги. По его приказу группой солдат было совершено покушение, но Зенону удалось заранее сбежать в Сердику (София).
В 469 г. он занимал консульство. После этого он был удостоен должности «магистр солдатских войск» восточных провинций. В этой роли он намеревался бороться с разбоями и бандитизмом исаврийского военачальника Индака.
Но амбициозность Зенона потерпела неудачу, когда Лев возвысил сына Аспара Патриция до чина Цезаря и обручил его со своей дочерью Леонтией. Более того, Аспар через своего старшего сына Ардабуриуса пытался заручиться поддержкой опоры силы Зенона, исаврийской гвардии, чтобы вернуть себе превосходство над своим соперником.
Зенон вернулся в Халкидон, откуда он мог влиять на дела в Константинополе. Попытки Аспара сделать своего сына наследником престола возмутили многих в столице, поскольку его арианские верования были ересью для ортодоксальных христиан Константинополя. Среди последовавших за этим беспорядков и беспорядков Зенон устроил убийство Аспара и Ардабурия (471 г. н.э.). Затем, в 473 году нашей эры, Зенон был назначен «магистром солдат» восточной империи, заняв место Аспара.
В октябре 473 г. Лев возвел своего пятилетнего внука, сына Зенона и Элии Ариадны, соправителем Льва II.18 января 474 г. Лев умер, и Лев II был единственным императором, а Зенон — регентом восточной империи. Но уже 9 февраля Сенат назначил Зенона соправителем Августа.
До того, как закончился 474 год нашей эры, Лев II умер. Ходили слухи, что Зенон убил собственного сына, чтобы занять трон. После своего воцарения Зенон имел хорошие отношения с Западом. Ибо нынешний западный император Юлий Непос был связан узами брака с женой Зенона.
Между тем отношения с вандалами ухудшились, так как король Гейзерих все еще был зол на убийство Аспара, земляка-немца, и явно предпочитал свое влияние на востоке влиянию Зенона.
Когда отношения настолько испортились, Гейзерих вторгся в Эпир и захватил Никополь. Хотя после этой первоначальной вражды договор был, увы, согласован, и мир был восстановлен.
Но как Гейзерих сначала обиделся, так и вождь остготов Теодорих Страбон воспользовался возможностью смерти Аспара, чтобы возобновить военные действия с восточной империей. После первых успехов его остановил исаврийский генерал Иллус.
Хотя сам Илл вскоре стал причиной неприятностей для Зенона, поскольку он стал участником заговора против императора в Константинополе.Заговор имел далеко идущие последствия, в него была вовлечена даже свекровь Зенона и вдова Льва, Элия Верина.
План состоял в том, чтобы свергнуть Зенона и вместо этого посадить на трон возлюбленного Элии Верины Патриция. Кроме того, в заговоре участвовали брат Иллуса Трокундес и брат Элии Верины Василиск.
Зенон, однако, получил предупреждение о том, что его жизнь в опасности, и бежал на свою родину, в Исаврию. Сенат, однако, отклонил Патриция как нового императора и вместо этого выбрал Василиска (475 г. н.э.).
Хотя правление Василиска продлилось недолго. Его правление было настолько непопулярным, что вскоре он потерял большую часть поддержки, которая привела его к власти.
Одним из ключевых моментов гибели Василиска было то, что Иллус, тот самый генерал, который замышлял заговор против Зенона, решил, что его правление было настолько плохим, что вместо этого он присоединится к Зенону и поможет ему вернуться к власти.
При поддержке Илла Зенон двинулся из Исаврии в сторону Константинополя. К тому времени Василиск был настолько непопулярен, что посланная против них армия под командованием Арматуса, любовника императрицы, намеренно избегала их, чтобы позволить им беспрепятственно пройти к столице.
Когда Зенон вновь вошел в свою столицу в августе 476 г. н.э., сопротивления просто не было. Одной из его первых ролей в качестве восстановленного императора было наблюдение за формальным концом западной империи, традиционно именуемым «падением Рима».
н.э., сопротивления просто не было. Одной из его первых ролей в качестве восстановленного императора было наблюдение за формальным концом западной империи, традиционно именуемым «падением Рима».
Если его первоначальный соратник Юлий Непос был изгнан из Италии и заменен Ромулом Августом, то новый император также был вынужден отречься от престола, когда Одоакр возглавил восстание немецких наемных войск в Италии.
Одоакр теперь требовал признания его правителем Италии, хотя, по крайней мере, предлагал сделать это от имени восточной империи.Было ли подчинение Одоакра восточному трону чисто теоретическим, не имеющим практического значения, оно, по крайней мере, позволяло надеяться на восток однажды вернуть итальянские территории от немцев.
Зенон признал Одоакра патрицием (патрицием) и правителем Италии, хотя настаивал на том, чтобы Юлий Непос продолжал, хотя и находился в изгнании, императором Запада.
Подробнее :
Закат Рима
Император Гликерий
Император Олибрий
Император Анфемий
ОТ СТРАНИЦЫ К СЦЕНЕ — ПУТЕШЕСТВИЕ ПО КАРИБСКИМ БАРАМ — Дань тринидадскому драматургу Зено Оби Констанс
BANANA BOAT PRODUCTIONS
Посвящение Карибскому драматургу 10643 Понедельник 10643 декабрь 909 Оби Констанс , 2018, Banana Boat Productions собрала ансамбль, состоящий из некоторых из самых известных карибских американских актеров Нью-Йорка, чтобы отдать дань уважения одному из самых знаковых драматургов региона, Зено Оби Констанс Мероприятие называлось «От страницы к сцене- Карибское путешествие », посвященное творчеству и наследию удостоенного наград тринидадского драматурга Зенона Оби Констанца. Мероприятие было представлено в TheaterLab Studios 357 West 37 th Street на Манхэттене. Продюсером и постановкой выступила Мерлина Рич, основатель и художественный руководитель Banana Boat Productions. Г-н Констанс является автором нескольких сценариев в репертуаре постановки Banana Boat , и его работы на протяжении более пятидесяти лет помогли исправить многие заблуждения, часто представляемые внешнему миру в отношении жителей Карибского бассейна. В честь г-на Констанса мы также отметили яркую и культурно значимую традицию создания театра в англоязычных странах Карибского бассейна, которая в основном неизвестна в США.С. и театральные сообщества Нью-Йорка. На счету г-на Констанса более 20 постановок, многие из которых широко разыгрывались по всему Карибскому региону и в диаспоре. Среди них De Roaring 70’s, The Road Made To Walk, Dueling Voices и, возможно, его самая известная работа, The Ritual. Ритуал стал обязательным чтением для студентов, изучающих английский язык и драму как в университетах, так и в старших классах школ по всему Карибскому региону. Среди его многочисленных национальных и региональных наград — премия Vanguard Cacique за его вклад в театральное искусство в средних школах Тринидада, Премия драматургов Национального совета за дуэльные голоса и Премия Министерства искусств и мультикультурализма Тринидада за его жизненные достижения в качестве обоих драматург и режиссер. Дань исследовала творчество г-на Констанса посредством постановочного чтения отрывков из нескольких его пьес, включая «Рассказ Агути», «История любви Патрисии» и «Синдром Золушки», а также видеопрезентации и отзывы от бывших соратников и бывших учеников. В актерский состав этого мероприятия вошли несколько удостоенных наград актеров карибского происхождения, в том числе Линкольн Браун, Ньянда Каммок, Акейл Дэвис, Дайанн Диксон, Эмилио Эванс, Марша Энн Хэй, Лори Синклер Минор и Карл О Брайан Уильямс. Мероприятие было бесплатным для публики. Благодаря щедрости The Puffin Foundation за большой успех этого вечера Фото Дуга Бэррона: На приведенной выше сцене отрывок из фильма «Синдром Золушки»: с Эмилло Эвансом и Няндой Каммок BANANA BOAT PRODUCTIONS Компания была основана в 1998 году для создания театральных представлений, представляющих особый интерес для англоязычного карибского сообщества столичного района Нью-Йорка.

 Наша основная предпосылка такова: карибская культура — это разноцветная и богатая палитра выражений, переживаний и стилей жизни, которая нуждается в большем раскрытии в царстве по-настоящему значимого театра. BBP ищет пьесы, которые сосредоточены на драматических темах, отражающих историческое и культурное развитие карибской жизни, а также нынешнюю реальность карибской культуры, которая утвердилась в других глобальных условиях. Мы даем наводящие на размышления и реалистичные театральные опыты людям, которые могут определить, осмыслить и оценить важность своей жизни.В этом контексте наши произведения можно рассматривать как эмпирические инструменты, способствующие большей проработке, более глубокому пониманию и более уважительному отношению к себе, в данном случае — карибскому «я». Прилагаются усилия, чтобы сохранить и проиллюстрировать выразительную формулировку и очень эффективные нюансы карибского языка, сделав его доступным для любой аудитории. Фоновые темы некоторых пьес, в которых разворачиваются драматические элементы, включают: 1) проблемы ассимиляции в более широкие этнические культуры и возникающие межпоколенческие конфликты, и 2) затяжные приспособления к постколониальной жизни, что иллюстрируется уважением к ней.
Наша основная предпосылка такова: карибская культура — это разноцветная и богатая палитра выражений, переживаний и стилей жизни, которая нуждается в большем раскрытии в царстве по-настоящему значимого театра. BBP ищет пьесы, которые сосредоточены на драматических темах, отражающих историческое и культурное развитие карибской жизни, а также нынешнюю реальность карибской культуры, которая утвердилась в других глобальных условиях. Мы даем наводящие на размышления и реалистичные театральные опыты людям, которые могут определить, осмыслить и оценить важность своей жизни.В этом контексте наши произведения можно рассматривать как эмпирические инструменты, способствующие большей проработке, более глубокому пониманию и более уважительному отношению к себе, в данном случае — карибскому «я». Прилагаются усилия, чтобы сохранить и проиллюстрировать выразительную формулировку и очень эффективные нюансы карибского языка, сделав его доступным для любой аудитории. Фоновые темы некоторых пьес, в которых разворачиваются драматические элементы, включают: 1) проблемы ассимиляции в более широкие этнические культуры и возникающие межпоколенческие конфликты, и 2) затяжные приспособления к постколониальной жизни, что иллюстрируется уважением к ней.


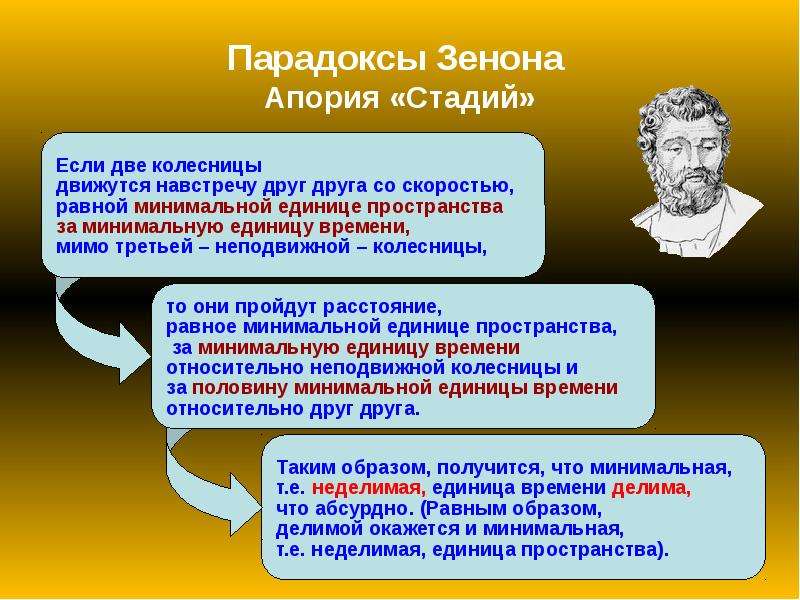

 Если за некоторое время первое из тел В пройдет мимо всех Г, то за это же время первое из тел Г пройдет мимо половины тел А, а значит, оно пройдет лишь половину того расстояния, который прошло тело В, а значит – так как В и Г движутся с равными скоростями – оно прошло и половину того времени, за которое тело В прошло все тела Г. С другой стороны, за одно и то же время первое из тел Г пройдет мимо всех В, а первое из В пройдет лишь половину тел А, и значит, в два раза меньшее расстояние, затратив в два раза меньшее время, чем тело Г, прошедшее все тела В. Получается, что одно и то же время и вдвое длиннее, и вдвое короче, чем оно же само.
Если за некоторое время первое из тел В пройдет мимо всех Г, то за это же время первое из тел Г пройдет мимо половины тел А, а значит, оно пройдет лишь половину того расстояния, который прошло тело В, а значит – так как В и Г движутся с равными скоростями – оно прошло и половину того времени, за которое тело В прошло все тела Г. С другой стороны, за одно и то же время первое из тел Г пройдет мимо всех В, а первое из В пройдет лишь половину тел А, и значит, в два раза меньшее расстояние, затратив в два раза меньшее время, чем тело Г, прошедшее все тела В. Получается, что одно и то же время и вдвое длиннее, и вдвое короче, чем оно же само.
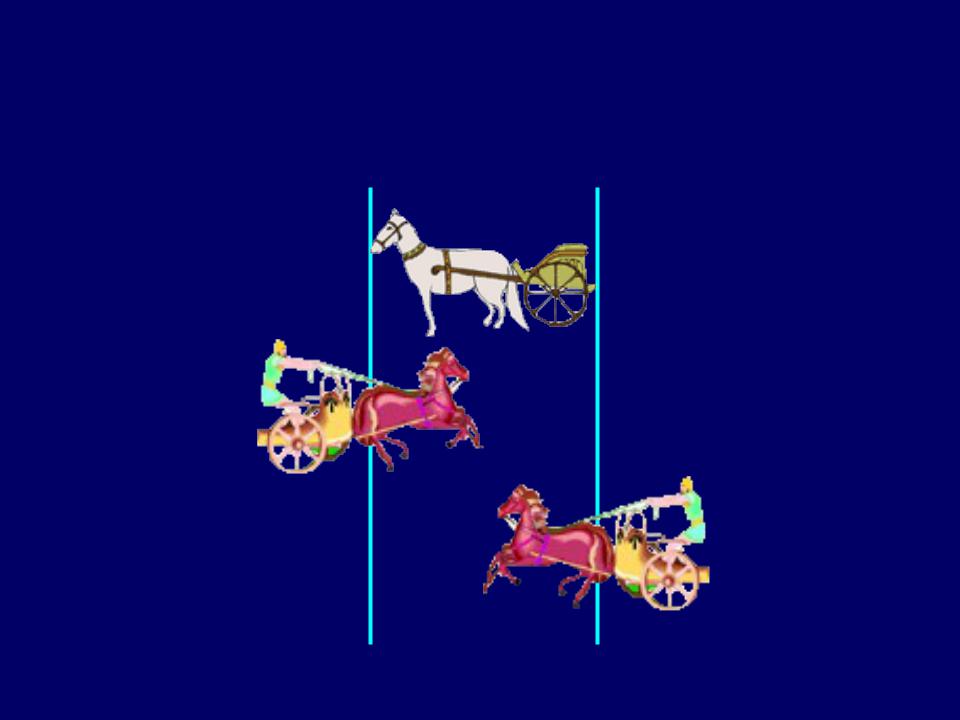 Так, Аристотель полагал, что пространство и время не состоят из некоторого числа отдельных точек и моментов, но представляют собой особый тип сущего – нечто непрерывное, или, как еще говорят, континуум (лат. continuum – непрерывное). Пространственные и временные отрезки в действительности делимы до бесконечности, но делимы лишь потенциально, в том смысле, что любой отрезок можно разделить некоторой точкой, то, что осталось, тоже можно разделить, и т. д., но невозможно в какой-то момент реализовать бесконечное количество делений, – точно так же, как всякий раз возможно продлить имеющийся отрезок на некоторую величину, но нельзя считать бесконечное число таких продлений уже реализованным. Невозможно иметь в наличии бесконечную прямую, и нельзя сказать, что на отрезке уже находится бесконечное количество точек. Вот если бы в первой апории идущий человек каждый раз, проходя середину очередного отрезка, останавливался бы, отмечая эту середину, – тогда его движение не было бы непрерывным и он никогда бы не смог пройти весь отрезок.
Так, Аристотель полагал, что пространство и время не состоят из некоторого числа отдельных точек и моментов, но представляют собой особый тип сущего – нечто непрерывное, или, как еще говорят, континуум (лат. continuum – непрерывное). Пространственные и временные отрезки в действительности делимы до бесконечности, но делимы лишь потенциально, в том смысле, что любой отрезок можно разделить некоторой точкой, то, что осталось, тоже можно разделить, и т. д., но невозможно в какой-то момент реализовать бесконечное количество делений, – точно так же, как всякий раз возможно продлить имеющийся отрезок на некоторую величину, но нельзя считать бесконечное число таких продлений уже реализованным. Невозможно иметь в наличии бесконечную прямую, и нельзя сказать, что на отрезке уже находится бесконечное количество точек. Вот если бы в первой апории идущий человек каждый раз, проходя середину очередного отрезка, останавливался бы, отмечая эту середину, – тогда его движение не было бы непрерывным и он никогда бы не смог пройти весь отрезок.