Теорема Пифагора — формула, доказательство, задачи

Сложно представить, но в научной литературе существует 367 доказательств теоремы Пифагора. В школьной программе мы проходим гораздо меньше — в этом материале познакомимся с главными формулами и их доказательствами.

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

a² + b² = c²,

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c² − b²
• b = √c² − a²
• c = √a² + b²

Запоминаем

в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c² < a² + b², значит угол, противолежащий стороне c, является острым.
• если c² = a² + b², значит угол, противолежащий стороне c, является прямым.
• если c² > a² +b², значит угол, противолежащий стороне c, является тупым.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a² + b² = c².

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

∠ACB =∠CHA = 90º,

∠A — общий.

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

∠ACB =∠CHB = 90º,

∠B — общий.

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a² = c * HB, b² = c * AH.
• Сложим полученные равенства:

a² + b² = c * HB + c * AH

a² + b² = c * (HB + AH)

a² + b² = c * AB

a² + b² = c * c

a² + b² = c²

Теорема доказана.

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁² = A₁C₁² + B₁C₁².
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

• Пусть катеты a = 6 и b = 8.

• По теореме Пифагора c² = a² + b².

• Подставим значения a и b в формулу:
  c² = 6² + 8² = 36 + 64 = 100
  c = √100 = 10.

Ответ: 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

Как решаем:

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

11² = 8² + 9²

121 ≠ 145

Ответ: треугольник не является прямоугольным.

---

---

 

 

Шпаргалки по математике родителей

Все формулы по математике под рукой

формула, доказательство и примеры решений

Содержание:

• Формула теоремы Пифагора
• Доказательство теоремы Пифагора
• Геометрическая формулировка теоремы Пифагора
• Примеры решения задач
• Историческая справка

Формула теоремы Пифагора

Теорема

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (рис. {2}$ было известно уже египтянам ещё около 2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Остались вопросы?

Здесь вы найдете ответы.

Как выглядит формула, отражающая смысл теоремы Пифагора?

Согласно теореме Пифагора, значение длины гипотенузы (с) треугольника с прямыми углами, возведенное в квадратную степень, является величиной, равной сумме его катетов (а и b), каждый из которых также возведен в квадрат. Наглядно и с применением условных обозначений это выглядит так:

a² + b² = c².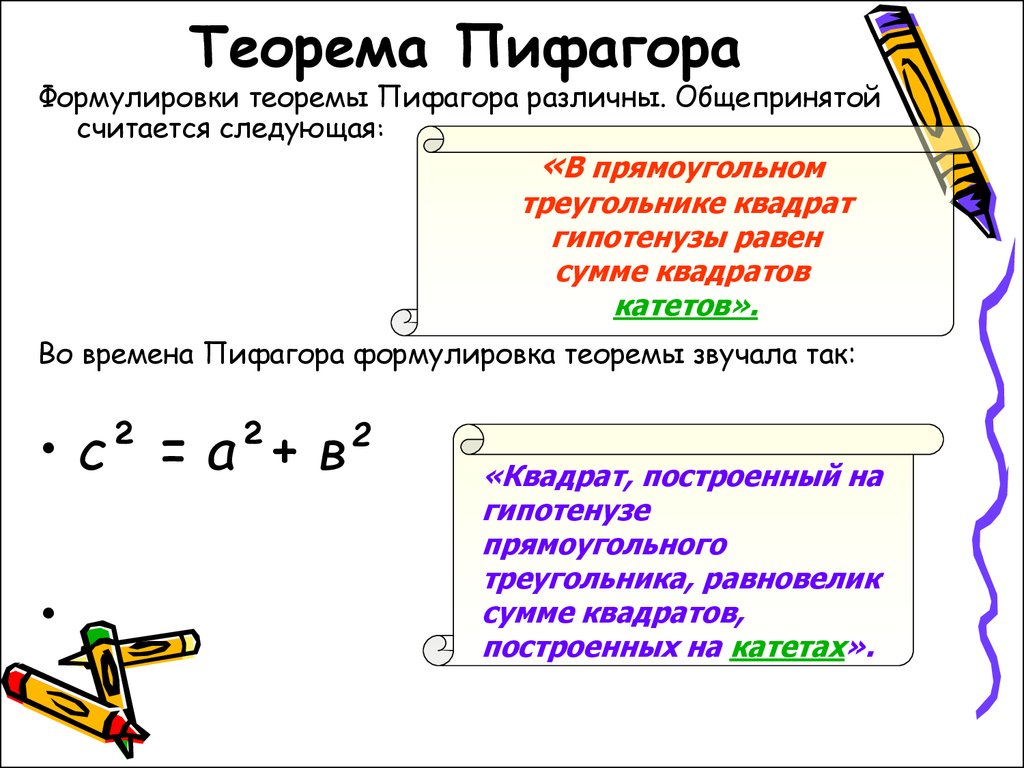

О чем гласит теорема Пифагора?

В теореме Пифагора говорится о том, что в треугольнике с прямыми углами сумма длин катетов, каждая из которых возведена в квадрат, равна длине его гипотенузы, также возведенной в квадратную степень.

При этом под гипотенузой понимается сторона, которая расположена противоположно прямому углу. Катетом считается одна из сторон, участвующих в образовании прямого угла.

Треугольник имеет прямой угол. Как доказать теорему Пифагора, которая гласит, что сумма квадратов катетов прямоугольного труегольника равна длине его гипотенузы, которая возведена в квадрат?

Основание прямоугольного треугольника обозначим как Н. Из его вершины С проведем высоту на гипотенузу АВ. Получившийся в результате этого треугольник АСН является подобным треугольнику АВС по двум углам, равным 90º (∠ACB =∠CHA).

В обоих треугольниках есть один общий угол — ∠A.

Подобными также являются треугольные фигуры АВС и СВН. Основанием их подобия являются прямые углы (∠ACB =∠CHB). Оба эти треугольника имеют общий угол, которым является ∠B.

Для продолжения доказательства теоремы Пифагора следует ввести дополнительные обозначения: BC = a, AC = b, AB = c.

На основании полученной ранее информации о подобии треугольников можно утверждать, что:

a/с = HB/a, b/с = AH/b.

Полученное равенство также позволяет сделать следующий вывод:

a2 = c * HB, b2 = c * AH.

На следующем этапе произведем сложение полученных ранее равенств:

a2 + b2 = c * HB + c * AH

Вынесем за скобки общий множитель во второй части равенства:

a2 + b2 = c * (HB + AH)

Теперь можно сократить Н в левой части равенства, в результате получим:

a2 + b2 = c * AB

В приведенных выше обозначениях указано, что АВ = с. Это позволяет переписать равенство следующим образом:

a2 + b2 = c * c, или a2 + b2 = c2

Таким образом, теорема Пифагора доказана.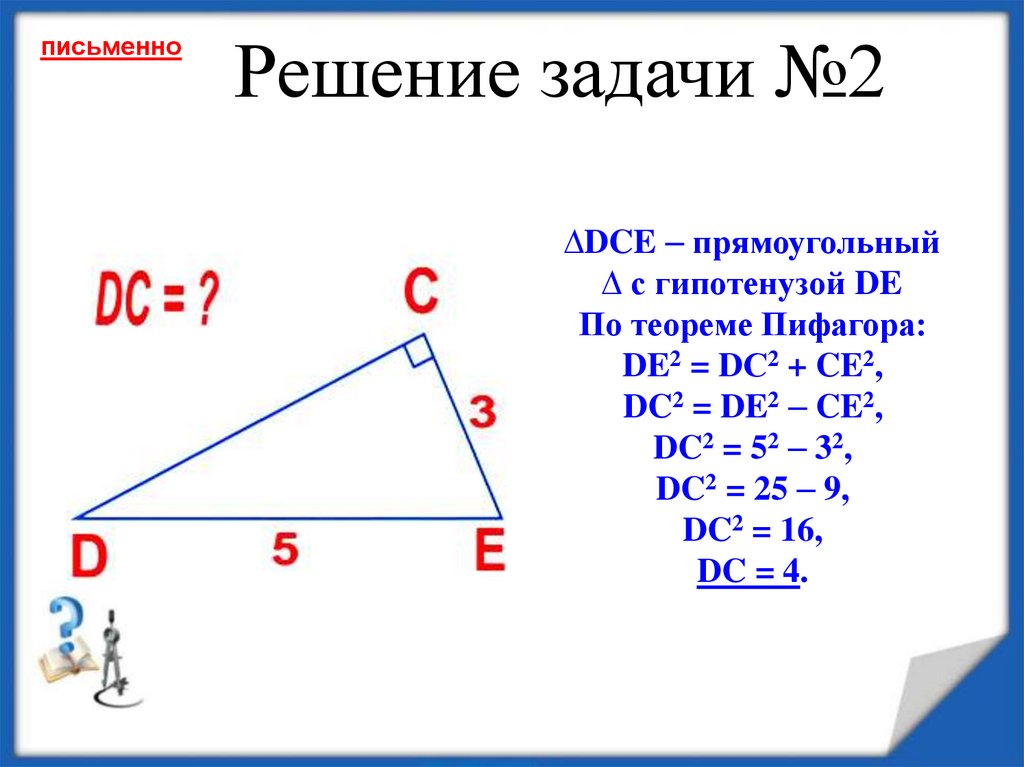 2

Извлечем квадрат из обеих частей равенства, в итоге получим:

x = √(5² + 5²)= √(25+25) = √50 = √25*2 = 5√2

Ответ: длина гипотенузы прямоугольного треугольника, катет которого равен 5 см, составляет 5√2, что равно примерно 7,07 см.

Применима ли теорема Пифагора к любому треугольнику?

Теорема Пифагора не может быть применима к треугольнику с тупыми или острыми углами. Она выполняется только в случае прямоугольного треугольника.

Для треугольника с углом 90º справедливо утверждение о том, что длина его гипотенузы, возведенная во вторую степень, равна сумме длин его катетов, взятых в квадрат.

Дан прямоугольный треугольник, длина гипотенузы которого равна 7 см, а одного катета – 6 см. Как вычислить длину второго катета, используя теорему Пифагора?

В теореме Пифагора говорится о том, что сумма длин катетов прямоугольного треугольника, возведенных во вторую степень, равна квадрату длины его гипотенузы. В случае с треугольником, некоторые параметры которого приведены в задании, это утверждение выглядит следующим образом:

х² = 7²-6² = 49-36 = 13.

Для того чтобы найти значение х, нужно извлечь квадратный корень из числа 13:

х =√13.

Ответ: Длина второго катета прямоугольного треугольника равна корню квадратному из 13.

Длина одного из стоящих рядом домов равна 24 м, высота второго из них составляет 16 м. Как вычислить расстояние между крышами обоих домов, зная, что квадрат гипотенузы равен сумме квадратов катетов?

Для решения поставленной задачи следует воспользоваться теоремой Пифагора, которая говорит о том, что сумма длин катетов треугольника с прямым углом, возведенных в квадрат, равна длине его гипотенузы, также возведенной во вторую степень:

a² + b² = c².

Теорема Пифагора может быть применима в данном случае по причине того, что образованная между двумя домами конструкция является прямоугольным треугольником.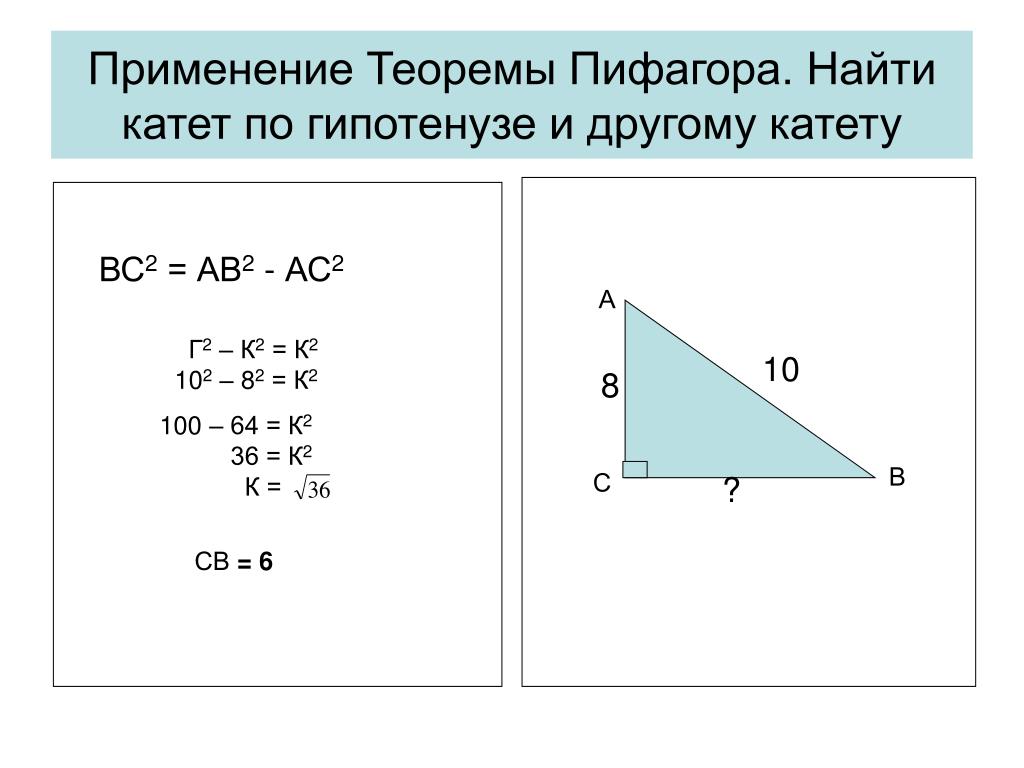 Зная о том, что сумма квадратов катетов в прямоугольном треугольнике равна длине его катета, возведенной в квадрат, можно вычислить длину неизвестного катета:

24 м – 16 м = 8 м.

Длина одного катета треугольника равна 16 м, второго – 8 м. Зная это, можно применить теорему Пифагора для вычисления длины гипотенузы:

(16*16) + (8*8) = 256 + 64 = 320 м.

Осталось только извлечь квадратный корень из 320, для того чтобы узнать длину расстояния между крышами двух домов.

Ответ: Расстояние между крышами домов равно корню квадратному из 320.

Длина гипотенузы треугольника с прямым углом равна 13 см. Один из его катетов равен 12 см. Как найти длину его второго катета по теореме Пифагора?

Обозначим длину неизвестного катета как х. Зная то, что по теореме Пифагора длина гипотенузы прямоугольного треугольника, возведенная во вторую степень, равна сумме длин его катетов, которые также возведены в квадрат, можно выразить длину неизвестного катета следующим образом:

х² = 132 – 122 = 169 – 144 = 25

Теперь, для того чтобы узнать длину второго катета, необходимо извлечь квадратный корень из числа 25:

х = √25 = 5

Ответ: длина второго катета прямоугольного треугольника равна 5 см.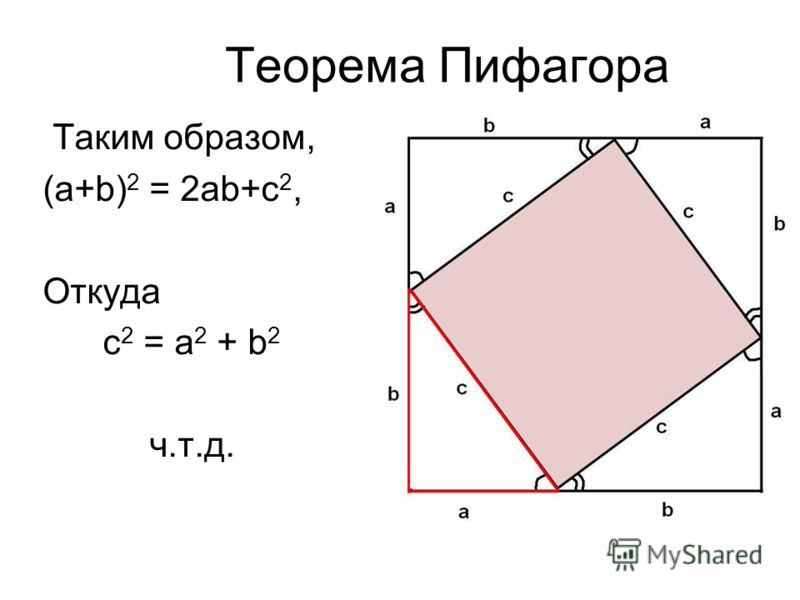

Дан треугольник с прямым углом, к гипотенузе которого проведена медиана длиной 6,5 м. Длина одного из катетов данного треугольника составляет 5 см. Как вычислить длину второго катета треугольника по теореме Пифагора?

Известно, что длина медианы (m), которая проведена к гипотенузе прямоугольного треугольника, равна ½ ее длины. Используя это, можно высчитать длину гипотенузы прямоугольного треугольника:

с = 2*m = 2*6,5 = 13 см.

Высчитав длину гипотенузы и зная длину одного из катетов прямоугольного треугольника, можно вычислить, чему равен его второй катет. Для этого можно использовать теорему Пифагора, согласно которой:

a²+b²=c²

В нашем случае:

5²+b²=13²

Выражаем из записанного выше равенства длину неизвестного катета:

b²=13²-5²= 144

Из полученного числа нужно извлечь квадратный корень, для того чтобы узнать длину второго катета прямоугольного треугольника:

b = √144 = 12 см.

Ответ: Длина второго катета прямоугольного треугольника равна 12 см.

Как можно вычислить треугольник, для которого по теореме Пифагора, соблюдается равенство f2=a2+ b2?

Равенство, указанное в задании, применимо к треугольнику с прямым углом, как гласит теорема Пифагора.

Каждая из сторон треугольника может быть обозначена прописной буквой, которая соответствует строчной букве, обозначающей угол треугольника, расположенный противоположно этой стороне. На основании этого можно сделать вывод о том, что искомый треугольник является прямоугольным и имеет гипотенузу f и катеты a и b:

∆АDF c ∠F= 90°

Ответ: имеется треугольник АDF с прямым углом F.

Существует ли теорема, которая обратна теореме Пифагора, и что она гласит?

Теорема, которая является обратной теореме Пифагора, существует. Согласно этой теореме, треугольник считается прямоугольным в том случае, если длина его большей стороны, возведенная в квадратную степень, равна сумме длин двух других его сторон, которые также возведены в квадратную степень.

Имеется равнобедренный треугольник, длина двух сторон которого равна 48 см, а третьей – 51 см. Как можно высчитать площадь данного треугольника по теореме Пифагора?

Для начала следует провести высоту (h) к основанию равнобедренного треугольника. Данная высота, проведенная к основанию, в случае с равнобедренным треугольником является медианой.

Теперь можно высчитать длину высоты, используя теорему Пифагора. Она будет равна:

h = √((48 см)² — (25,5 см)²) = 10,5√15 см.

Площадь (S) треугольника рассчитывается путем деления на число, полученное в результате умножения длины высоты на длину основания треугольника:

S = ½*10,5√15 см*51 см = 267,75√15 см².

Ответ: Площадь треугольника равна 267,75√15 см².

Каким образом можно вычислить высоту равностороннего треугольника со стороной а по теореме Пифагора?

В равностороннем треугольнике высота (h), проведенная к его основанию, является также его биссектрисой и медианой. Она делит равносторонний треугольник на две части, которые являются равными треугольниками с прямым углом. Их гипотенуза равна а, а катеты – а/2. Для ответа на поставленный вопрос следует применить теорему Пифагора:

h²=a²-(a/2)²=a²-(a²/4)=3a²/4

h=a√3/2.

Дан треугольник с прямым углом, длина одного из катетов которого вдвое меньше длины его второго катета. Гипотенуза данного треугольника равна корню квадратному из 15. Как по теореме Пифагора вычислить длину меньшего из катетов треугольника?

Обозначим меньший из катетов как х. Тогда другой катет, длина которого в два раза больше, будет обозначен как 2х. Если в случае с прямоугольным треугольником, длина гипотенузы которого равна √15, применить теорему Пифагора, то она будет выглядеть следующим образом:

(2х)²+(x)²=√15

После раскрытия скобок в уравнении получаем следующее равенство:

4х²+x²=15

Складываем слагаемые в первой части и получаем:

5x²=15

Сокращаем обе части уравнения на 5, и в итоге получается, что:

x²=3

Это значит, что:

x=√3

Ответ: Длина меньшего из катетов треугольника равна √3, а большего – 2√3.

Известно, что длина одного из катетов прямоугольного треугольника составляет 60 см, а длина его гипотенузы и второго катета в сумме дают 180 см. Можно ли по теореме Пифагора высчитать длину гипотенузы данного треугольника?

Если обозначить длину неизвестного катета через х, то гипотенуза будет равна 180-х. Используя введенные обозначения, запишем теорему Пифагора для данного треугольника:

x²+60²=(180-x)² = x²+3600=32400-360x+x²

После сокращений получается следующее равенство:

360х=32400-3600=28800

Теперь можно найти значение х:

х=28800/360=80

Длина второго катета равна 80 см.

Зная, что катет в 80 см и неизвестная длина гипотенузы в сумме дают 180 см, можно вычислить длину гипотенузы:

180-80=100 см.

Ответ: Длина гипотенузы равна 100 см.

Дана прямоугольная трапеция ABCD. Ее углы А и В равны по 90°. Длины боковых сторон данной трапеции составляют 9 см и 18 см. Диагональ АС составляет 15 см. Как можно вычислить длину основания трапеции по теореме Пифагора?

АВСD является прямоугольной трапецией, у которой AB=9 см и CD=18 см. Диагональ АС данной трапеции составляет 15 см. При этом ВС и AD остаются неизвестными величинами. Длину ВС можно вычислить по следующей формуле:

√15²-9²=√144=12 см.

Произведем перенос высоты:

СС1=АВ=9 см.

Тогда получаем, что:

C1D=√18²-9²=9√3

BC=AC1=12

AD=12+9√3 см.

Ответ: Длина основания AD прямоугольной трапеции равна 12+9√3 см.

Теорема Пифагора (Пифагора) — Формула, Доказательство, Примеры

Теорема Пифагора , также называемая теоремой Пифагора, объясняет взаимосвязь между тремя сторонами прямоугольного треугольника. По теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон треугольника. Давайте узнаем больше о теореме Пифагора, ее выводах и уравнениях, за которыми следуют решенные примеры треугольника и квадратов теоремы Пифагора.

1.	Что такое Теорема Пифагора?
2.	История теоремы Пифагора
3.	Теорема Пифагора Формула
4.	Доказательство теоремы Пифагора
5.	Теорема Пифагора Треугольники
6.	Квадраты теоремы Пифагора
7.	Приложения теоремы Пифагора
8.	Часто задаваемые вопросы по теореме Пифагора

Что такое Теорема Пифагора?

Теорема Пифагора утверждает, что если треугольник прямоугольный (90 градусов), то квадрат гипотенузы равен сумме квадратов двух других сторон. Обратите внимание на следующий треугольник ABC, в котором имеем ВС ² = АВ ² + АС ² . Здесь АВ — основание, АС — высота (высота), ВС — гипотенуза. Следует отметить, что гипотенуза является наибольшей стороной прямоугольного треугольника.

Уравнение теоремы Пифагора

Уравнение теоремы Пифагора выражается следующим образом: две другие ноги. Следовательно, любой треугольник с одним углом, равным 90 градусов дает треугольник Пифагора, и уравнение Пифагора может быть применено к треугольнику.

История теоремы Пифагора

Теорема Пифагора была введена греческим математиком Пифагором Самосским. Он был древним ионийским греческим философом. Он сформировал группу математиков, которые религиозно работали над числами и жили как монахи. Наконец, греческий математик сформулировал теорему, поэтому она была названа в его честь «теоремой Пифагора». Хотя он был введен много веков назад, его применение в нынешнюю эпоху обязательно для решения прагматических ситуаций.

Хотя Пифагор ввел и популяризировал эту теорему, существует достаточно свидетельств, подтверждающих ее существование в других цивилизациях за 1000 лет до рождения Пифагора. Самые старые известные свидетельства датируются периодом между 20-м и 16-м веками до нашей эры в старовавилонский период.

Формула теоремы Пифагора

Формула теоремы Пифагора утверждает, что в прямоугольном треугольнике ABC квадрат гипотенузы равен сумме квадратов двух других катетов. Если АВ и АС — стороны, а ВС — гипотенуза треугольника, то: ВС ² = АВ ² + АС ² ​. В этом случае АВ — основание, АС — высота или высота, а ВС — гипотенуза.

Другой способ понять формулу теоремы Пифагора — использовать следующий рисунок, который показывает, что площадь квадрата, образованного самой длинной стороной прямоугольного треугольника (гипотенузой), равна сумме площадей квадратов, образованных две другие стороны прямоугольного треугольника.

В прямоугольном треугольнике формула теоремы Пифагора выражается как:

c ² = a ² + b ²

Где,

• ‘c’ = гипотенуза прямоугольного треугольника
• «a» и «b» — две другие ноги.

Доказательство теоремы Пифагора

Теорему Пифагора можно доказать разными способами. Одними из наиболее распространенных и широко используемых методов являются алгебраический метод и метод подобных треугольников. Давайте посмотрим на оба этих метода по отдельности, чтобы понять доказательство этой теоремы.

Доказательство формулы теоремы Пифагора с использованием алгебраического метода

Доказательство теоремы Пифагора можно получить с помощью алгебраического метода. Например, давайте использовать значения a, b и c, как показано на следующем рисунке, и выполнить шаги, указанные ниже:

• Шаг 1: Расположите четыре конгруэнтных прямоугольных треугольника в заданном квадрате PQRS, стороной которого является a + б. Четыре прямоугольных треугольника имеют основание «b», высоту «a» и гипотенузу «c».
• Шаг 2: 4 треугольника образуют внутренний квадрат WXYZ, как показано, с четырьмя сторонами «с».
• Шаг 3: Площадь квадрата WXYZ при расположении четырех треугольников равна c ² .
• Шаг 4: Площадь квадрата PQRS со стороной (a + b) = площадь 4 треугольников + площадь квадрата WXYZ со стороной «c». Это означает (a + b) ² = [4 × 1/2 × (a × b)] + c ² . Это приводит к a ² + b ² + 2ab = 2ab + c ² . Следовательно, a ² + b ² = c ² . Значит доказано.

Формула теоремы Пифагора Доказательство с использованием подобных треугольников

Два треугольника называются подобными, если их соответствующие углы имеют одинаковую меру и их соответствующие стороны находятся в одном и том же отношении. Кроме того, если углы имеют одинаковую меру, то, используя закон синусов, мы можем сказать, что соответствующие стороны также будут в том же отношении. Следовательно, соответствующие углы в подобных треугольниках приводят нас к равным отношениям длин сторон.

Формула вывода теоремы Пифагора

Рассмотрим прямоугольный треугольник ABC с прямым углом в точке B. Проведите перпендикуляр BD, пересекающий AC в точке D. А (общий)

∠ADB = ∠ABC (оба угла прямые)

Таким образом, 4ABD ∼ 4ACB (по критерию подобия AA)

Аналогично можно доказать 4BCD ∼ △ACB.

Таким образом, △ABD ∼ △ACB, Следовательно, AD/AB = AB/AC. Мы можем сказать, что AD × AC = AB ² .

Аналогично, △BCD ∼ △ACB. Следовательно, CD/BC = BC/AC. Мы также можем сказать, что CD × AC = BC ² .

Складывая эти 2 уравнения, мы получаем AB ² + BC ² = (AD × AC) + (CD × AC)

AB ² + BC ² =AC(AD +DC)

5

5

5

AB ² + BC ² =AC ²

Отсюда доказано.

Теорема Пифагора Треугольники

Прямоугольные треугольники подчиняются правилу теоремы Пифагора и называются треугольниками по теореме Пифагора. Три стороны такого треугольника в совокупности называются тройками Пифагора. Все треугольники по теореме Пифагора следуют теореме Пифагора, которая гласит, что квадрат гипотенузы равен сумме двух сторон прямоугольного треугольника. Это можно выразить как c ² = а ² + б ² ; где «с» — гипотенуза, а «а» и «b» — катеты треугольника.

Теорема Пифагора Квадраты

Согласно теореме Пифагора, площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на двух других сторонах. Эти квадраты известны как квадраты Пифагора.

Приложения теоремы Пифагора

Применение теоремы Пифагора можно увидеть в нашей повседневной жизни. Вот некоторые из приложений теоремы Пифагора.

• Машиностроение и строительство

Большинство архитекторов используют технику теоремы Пифагора для нахождения неизвестных размеров. Когда известна длина или ширина, очень легко вычислить диаметр конкретного сектора. Он в основном используется в двух измерениях в инженерных областях.

• Распознавание лиц в камерах наблюдения

Функция распознавания лиц в камерах безопасности использует концепцию теоремы Пифагора, то есть расстояние между камерой безопасности и местоположением человека отмечается и хорошо проецируется через объектив с использованием концепции.

• Изделия из дерева и дизайн интерьера

Концепция Пифагора применяется в дизайне интерьеров и архитектуре домов и зданий.

• Навигация

Люди, путешествующие по морю, используют эту технику, чтобы найти кратчайшее расстояние и маршрут, чтобы добраться до нужных им мест.

☛ Статьи по теме

• Формулы прямоугольного треугольника
• Теорема о катете гипотенузы
• Подобные треугольники
• Теорема Пифагора Рабочие листы

Часто задаваемые вопросы по теореме Пифагора

Что такое теорема Пифагора в математике?

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Эта теорема может быть выражена как c ² = a ² + b ² ; где «с» — гипотенуза, а «а» и «b» — катеты треугольника. Эти треугольники также известны как треугольники теоремы Пифагора.

Что такое обратная теорема Пифагора?

Теорема Пифагора, обратная: если сумма квадратов любых двух сторон треугольника равна квадрату третьей (наибольшей) стороны, то треугольник называется прямоугольным.

В чем польза формулы теоремы Пифагора?

Теорема Пифагора работает только для прямоугольных треугольников. Когда известны любые два значения, мы можем применить теорему Пифагора и вычислить неизвестные стороны треугольника. Есть и другие реальные приложения теоремы Пифагора, например, в области инженерии и архитектуры.

Каково применение теоремы Пифагора в реальной жизни?

Теорема Пифагора используется в различных областях. Ниже приведены некоторые из его применений.

• Архитектура, строительство и судоходство.
• Для вычисления расстояния между точками на плоскости.
• Для расчета периметра, площади поверхности, объема геометрических фигур и т. д.

Можно ли применить формулу теоремы Пифагора к любому треугольнику?

Нет, теорему Пифагора можно применить только к прямоугольному треугольнику, поскольку теорема Пифагора выражает отношение между сторонами треугольника, где квадрат двух катетов равен квадрату третьей стороны, которая является гипотенузой. .

Как вычислить теорему Пифагора?

Теорему Пифагора можно использовать для нахождения неизвестной стороны прямоугольного треугольника. Например, если два катета прямоугольного треугольника равны 4 единицам и 6 единицам, то гипотенузу (третью сторону) можно рассчитать по формуле c ² = а ² + б ² ; где «с» — гипотенуза, а «а» и «b» — два катета. Подставляя значения в формулу, c ² = a ² + b ² = c ² = 4 ² + 6 ² = 16 + 36 = √52 = 7,2 единицы.

Что такое формула теоремы Пифагора?

Формула теоремы Пифагора выражается следующим образом: Гипотенуза ² = Основание ² + Высота ² . Это также пишется как c ² = а ² + б ² ; где «с» — гипотенуза, а «а» и «b» — катеты прямоугольного треугольника. Используя формулу теоремы Пифагора, можно вычислить любую неизвестную сторону прямого угла, если известны две другие стороны.

Почему важна теорема Пифагора?

Теорема Пифагора важна, потому что она помогает вычислить неизвестную сторону прямоугольного треугольника. У него есть и другие реальные приложения в области архитектуры и инженерии, навигации и так далее.

Правило Пифагора — Xcelerate Math

Теорема Пифагора (прописью):
Квадрат гипотенузы равен сумме квадратов двух других сторон.

Правило Пифагора (в символах):
Чтобы найти гипотенузу c ² = a ² + b ²
Чтобы найти другую сторону a ² = c ² – b ²

c всегда является гипотенузой.

Не забудьте найти квадратный корень из из на последнем шаге.

Знаете ли вы, что…?

Пифагор был 6 ^-й век до н.э. Греческий философ, математик и основатель религиозного культа по имени Пифагорейцы , верившие в реинкарнацию. Он играл активную роль в политике, но был вынужден бежать из дома, когда его учение стало непопулярным. Сейчас он наиболее известен своим Теорема Пифагора и Пифагорейские тройки .

Вопрос — Правило Пифагора для квадратов с тремя сторонами

Вот прямоугольный треугольник со сторонами 3, 4 и 5.
Используя площади квадратов, вы можете видеть, что 3 ² + 4 ² = 5 ²
С другими номерами работает?

Математическое развлечение. Правило Пифагора с полукругами с трех сторон

Работает ли правило Пифагора с площадями фигур, отличных от квадратов? Вычислите площади этих полукругов. Что ты заметил?

Пример первый. Нахождение гипотенузы

Найдите гипотенузу прямоугольного треугольника, перпендикулярные стороны которого равны 5 и 12.

Ответ:
а = 5
b = 12

c ² = a ² + b ²
= 5 ² + 12 ²
= 25 + 144
= 169

c = √169 (Не забудьте найти квадратный корень.)
= 13

---

Пример второй — нахождение гипотенузы

Плотник, строящий эти лестницы, должен рассчитать длину опорной деревянной балки внизу. вертикальный и горизонтальный длина 200 см и 210 см .

Ответ:
а = 200
b = 210

c ² = a ² + b ²
= 200 ² + 210 ²
= 4401000
= 84100

c = √84100 (Не забудьте найти квадратный корень.)
= 290 см

---

Пример третий. Нахождение стороны

В прямоугольном треугольнике гипотенуза равна 10 . Одна сторона равна 8 . Какова длина другой стороны ?

Ответ:
с = 10
b = 8

a ² = c ² – b ²
= 10 ² – 8 ²
= 100 – 64
= 36

а = √36
= 6

---

Пример четвертый — Нахождение стороны

Парашютист не падает прямо вниз, а сдувается ветром, как показано на схеме. В прямоугольном треугольнике гипотенуза равна 26 метрам а вертикальное падение составляет 24 метра . На какое расстояние по горизонтали она не попадет в цель приземления?

Ответ:
с = 26 метров
b = 24 метра

a ² = c ² – b ²
= 26 ² – 24 ²
= 676 – 576
= 100

а = √100
= 10 метров от цели

Вопросы

Q1. Чему равна гипотенуза прямоугольного треугольника, перпендикулярные стороны которого равны 26 и 168?

Q2.