Открытая Математика. Функции и Графики. Готфрид Лейбниц

Лейбниц (Leibniz) Готфрид Вильгельм (1.7.1646, Лейпциг, – 14.11.1716, Ганновер), немецкий философ-идеалист, математик, физик и изобретатель, юрист, историк, языковед. Изучал юриспруденцию и философию в Лейпцигском и Йенском университетах. В 1672 отправился с дипломатической миссией в Париж, а через четыре года возвратился в Германию, состоя в последующие 40 лет на службе у ганноверских герцогов, сначала в качестве придворного библиотекаря, затем – герцогского историографа и тайного советника юстиции. В 1700 стал первым президентом созданного по его инициативе Берлинского научного общества. В 1711, 1712 и 1716 встречался с Петром I, разработал ряд проектов по развитию образования и государственного управления в России. Вёл обширную переписку почти со всеми крупнейшими учёными, а также политическими деятелями.

В философии Лейбниц явился завершителем философии XVII в., предшественником немецкой классической философии. Его философская система сложилась к 1685 как итог двадцатилетней эволюции, в процессе которой Лейбниц критически переработал основные идеи Демокрита, Платона, Августина, Декарта, Гоббса, Спинозы и др. Лейбниц стремился синтезировать всё рациональное в предшествующей философии с новейшим научным знанием на основе предложенной им методологии, важнейшими требованиями которой были универсальность и строгость философских рассуждений. Совершенство действительного мира он понимал как «гармонию сущности и существования»: оптимальность отношений между разнообразием существующих вещей и действий природы и их упорядоченностью; минимум средств при максимуме результата. Следствиями последнего онтологического принципа является ряд других принципов: принцип единообразия законов природы, или всеобщей взаимосвязи, закон непрерывности, принцип тождества неразличимых, а также принципы всеобщего изменения и развития, простоты, полноты и др.

В духе рационализма XVII в. Лейбниц различал мир умопостигаемый, или мир истинно сущего (метафизическая реальность), и мир чувственный, или только являющийся (феноменальный) физический мир.

Реальный мир, по Лейбницу, состоит из бесчисленных психических деятельных субстанций, неделимых первоэлементов бытия – монад, которые находятся между собой в отношении предустановленной гармонии. Гармония (взаимнооднозначное соответствие) между монадами была изначально установлена богом, когда тот избрал для существования данный «наилучший из возможных миров». В силу этой гармонии, хотя ни одна монада не может влиять на другие (монады как субстанции не зависят друг от друга), тем не менее развитие каждой из них находится в полном соответствии с развитием других и всего мира в целом. Это происходит благодаря заложенной богом способности монад представлять, воспринимать, или выражать и отражать, все другие монады и весь мир. Деятельность монад состоит в смене восприятий (перцепций) и определяется индивидуальным «стремлением» (аппетицией) монады к новым восприятиям. Хотя вся эта деятельность исходит из самой монады, она в то же время есть развёртывание изначально заложенной в монаде индивидуальной программы, «полного индивидуального понятия», которое во всех подробностях бог мыслил, прежде чем сотворил данный мир. Т. о., все действия монад полностью взаимосвязаны и предопределены. Монады образуют восходящую иерархию сообразно тому, насколько ясно и отчётливо они представляют мир. В этой иерархии особое место занимают монады, которые способны не только к восприятию, перцепции, но и к самосознанию, апперцепции и к которым Лейбниц относил души людей.

Мир физический, как считал Лейбниц, существует только как несовершенное, чувственное выражение истинного мира монад, как феномен познающего объективный мир человека. Однако, поскольку физические феномены в конце концов порождаются стоящими за ними реальными монадами, Лейбниц считал их «хорошо обоснованными», оправдывая тем самым значимость физических наук. В качестве таких «хорошо обоснованных» феноменов ученый рассматривал пространство, материю, время, массу, движение, причинность, взаимодействие, как они понимались в физике и механике его времени.

В физике Лейбниц развивал учение об относительности пространства, времени и движения. Он установил в качестве количественной меры движения «живую силу» (кинетическую энергию) – произведение массы тела на квадрат скорости, в противоположность Декарту, который считал мерой движения произведение массы на скорость – «мёртвую силу», как назвал её Лейбниц. Использовав отчасти результаты Гюйгенса, Лейбниц открыл закон сохранения «живых сил», явившийся первой формулировкой закона сохранения энергии, а также высказал идею о превращении одних видов энергии в другие. Исходя из философского принципа оптимальности всех действий природы, Лейбниц сформулировал один из важнейших вариационных принципов физики – «принцип наименьшего действия» (позднее – принцип Мопертюи). Ему принадлежит также ряд открытий в специальных разделах физики: в теории упругости, теории колебаний, в частности открытие формулы для расчёта прочности балок и т.д.

В логике Лейбниц развил учение об анализе и синтезе, впервые сформулировал закон достаточного основания, ему принадлежит также принятая в современной логике формулировка закона тождества. В его работе «Об искусстве комбинаторики», написанной в 1666, предвосхищены некоторые моменты современной математической логики; Лейбниц выдвинул идею применения в логике математической символики и построений логических исчислений, поставил задачу логического обоснования математики, предложил использовать бинарную систему счисления для целей вычислительной математики.

Лейбниц впервые высказал мысль о возможности машинного моделирования человеческих функций; ввёл термин «модель».

В математике важнейшей заслугой Лейбница является разработка (наряду с Ньютоном и независимо от него) дифференциального и интегрального исчисления. Первые результаты были получены Лейбницем в 1675 под влиянием Гюйгенса и на основе работ Паскаля, Декарта, Валлиса и Меркатора. Систематический очерк дифференциального исчисления был впервые опубликован в 1684, интегрального – в 1686. Здесь давались определения дифференциала и интеграла, были введены знаки для дифференциала d и интеграла ∫, приводились правила дифференцирования суммы, произведения, частного, любой постоянной степени, функции от функции (инвариантность первого дифференциала), правила отыскания и различения (с помощью второго дифференциала) экстремальных точек кривых и отыскание точек перегиба, устанавливался взаимно-обратный характер дифференцирования и интегрирования. Применяя своё исчисление к ряду задач механики (о циклоиде, цепной линии, брахистохроне и др.

), Лейбниц наряду с Гюйгенсом и братьями Бернулли вплотную подходит к созданию вариационного исчисления (1686–96). В дальнейших работах Лейбниц указал (1695) формулу для многократного дифференцирования произведения (формула Лейбница) и правила дифференцирования ряда важнейших трансцендентных функций, положил начало (1702–03) интегрированию рациональных дробей. Лейбниц широко пользовался разложением функций в бесконечные степенные ряды, установил признак сходимости знакочередующегося ряда, дал решение в квадратурах некоторых типов обыкновенных дифференциальных уравнений. Лейбниц ввёл термины «дифференциал», «дифференциальное исчисление», «дифференциальное уравнение», «функция», «переменная», «постоянная», «координаты», «абсцисса», «алгебраические и трансцендентные кривые», «алгоритм» (в смысле, близком к современному) и др. Хотя предпринятые Лейбницем попытки логического обоснования дифференциального исчисления нельзя признать успешными, его ясное понимание существа новых аналитических методов и всесторонняя разработка аппарата исчисления способствовали тому, что именно его вариант исчисления во многом определил дальнейшее развитие математического анализа. Кроме анализа, Лейбниц сделал ряд важных открытий в других областях математики: в комбинаторике, алгебре (начала теории определителей), в геометрии, где он заложил основы теории соприкосновения кривых (1686), разрабатывал одновременно с Гюйгенсом теорию огибающих семейства кривых (1692–94), выдвинул идею геометрических исчислений.

В работе «Протогея» (1693) Лейбниц высказал мысль об эволюции Земли и обобщил собранный им материал в области палеонтологии. В биологию Лейбниц ввёл идею целостности органических систем, принцип несводимости органического к механическому; эволюцию он понимал как непрерывное развёртывание преформированных зародышей. В психологии ученый выдвинул понятие бессознательно «малых перцепций» и развил учение о бессознательной психической жизни.

В языкознании Лейбниц создал теорию исторического происхождения языков, дал их генеалогическую классификацию, развил учение о происхождении названий. Лейбниц явился одним из создателей немецкого философского и научного лексикона.

Основные философские сочинения: «Рассуждение о метафизике» (1685), «Новая система природы» (1695), «Новые опыты о человеческом разуме» (1704), «Теодицея» (1710), «Монадология» (1714). Основные математические сочинения: «Об истинном отношении круга к квадрату» (1682), «Новый метод максимумов и минимумов» (1684), «О скрытой геометрии и анализе неделимых…» (1686). Физические воззрения Лейбница изложены, в частности, в работах «Доказательство памятной ошибки Декарта» (1686), «Очерк динамики» (1695), политические и юридические идеи – в сочинениях «Трактат о праве…» (1667), «Христианнейший Марс…» (1680), «Кодекс международного дипломатического права» (1693) и др.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».

Универсальный гений Готфрида Вильгельма Лейбница

14 ноября прошло 300 лет со дня смерти Готфрида Вильгельма Лейбница (1. 07.1646 -14.11.1716) — немецкого философа, ученого, политика, дипломата, одного из самых универсальных гениев в истории человечества.

Лейбниц оставил научное наследие в математике, механике, философии, теологии, юриспруденции, истории, политике, языкознании, геологии, палеонтологии, психологии, педагогике.

Он был юристом, политиком, дипломатом, публицистом, организатором науки, инженером, изобретателем. Он переписывался почти со всеми философами, учеными, политиками тогдашней Европы: написал около 20 000 писем до 1100 человек.

Как мыслитель Лейбниц имел три уникальные черты. Он был очень проницательным — находил новое в общеизвестном и дополнял то, что считалось завершенным; часто высказывал идеи, на основе которых впоследствии возникали новые науки и научные направления. Он умел гармонично сочетать то, что другие считали несовместимым — идеи схоластической и новой философии, веру и разум. Он осмысливал чрезвычайно широкий диапазон вопросов — от фундаментальных принципов философии и науки к проектированию машин и решению текущих проблем международной политики.

Немного о жизненном пути Лейбница [Лейпциг (1646-1667)]

Лейбниц (Gottfried Wilhelm Leibniz) родился 1 июля 1646 г., за два года до окончания Тридцатилетней войны, которая принесла большие беды Германии. Его отец, юрист по образованию, был профессором философии морали (этики) Лейпцигского университета. Один его дед был профессором римского права того же университета, второй служил в горном ведомстве. В шестилетнем возрасте Готфрид потерял отца, после которого осталась большая библиотека. В семь лет мальчик стал посещать городскую школу, где с первого года обучения изучал латынь. Он очень любил читать (читал на немецком с шести лет).

Когда Готфриду было восемь лет, в его руки попала иллюстрированная «Римская история» Ливия. Имея лишь начальные знания по латыни, он стал читать подписи к иллюстрациям и пытался понять прочитанное. Затем вернулся к началу книги и стал понимать больше. После нескольких повторов понял уже почти всю книгу. Мать надлежащим образом оценила достижения сына и позволила ему пользоваться родительской библиотекой. Много лет спустя Лейбниц вспоминал: «Я был рад, что наконец увидел античных авторов, которых до того знал лишь по именам: Цицерон и Сенека, Плиний, Геродот, Ксенофонт, Платон, историков времен империи и многих латинских и греческих отцов церкви». В 12 лет он был уже знатоком латыни.

В последнем классе школы изучали логику. Этот предмет произвел очень большое впечатление на юного Лейбница. Его восхитило то, что предикаменты (категории) образовывали будто всеобщий реестр вещей. У него появилась идея создать нечто подобное для суждений, а также нечто вроде алфавита человеческих мыслей, комбинируя знаки которого, можно было бы получать новые знания. Эта идея станет впоследствии одной из руководящих в его научном творчестве.

В 1661 г. Готфрид вступил в Лейпцигский университет. Большое впечатление на него произвел профессор риторики Якоб Томазий, который читал лекции по древнегреческой и древнеримской литературе и очень высоко оценивал философию Аристотеля. Лейбниц самостоятельно ознакомился с некоторыми произведениями Ф. Бэкона, Й.Кеплера, Галилея, Р. Декарта, Т. Гоббса, П.Гассенди и других философов и ученых. Впоследствии он вспоминал, что в 15-летнем возрасте целыми днями размышлял о выборе между Аристотелем и Демокритом, между схоластической и механистической философией. Тогда он предпочел механистическую философию — стал сторонником философии Галилея, Декарта, Гоббса, но впоследствии подверг ее критике, и дальше всю жизнь пытался найти компромисс между аристотелизмом и механицизмом. Следует также заметить, что Лейбниц был глубоко верующим человеком и всю жизнь пытался совместить религию и науку, не допуская сомнений в догматах христианской веры.

В 1663 г. Лейбниц получил степень бакалавра философии, защитив на диспуте работу «метафизическая диспутациях о принципе индивидуума», которая вышла в печати с похвальным предисловием Томазия. Во время летнего семестра 1663г. он слушал в Иенском университете лекции по математике Эдуарда Вейгеля — большого энтузиаста идеи неограниченного применения математики и математических методов во всех областях знаний. Вейгель выдал работу «Идея математико-философской энциклопедии», пытался математически доказать христианские догматы.

Вернувшись в Лейпциг, Лейбниц в 1664-1666 гг. подготовил и защитил три диспутации, получив последовательно степени магистра философии, бакалавра юриспруденции, магистра философии pro loco ( «для данного места»). Последняя степень давала право на чтение лекций в Лейпцигском университете. В первой работе юридические вопросы освещались с точки зрения философии, во второй была попытка рассматривать юридические проблемы в математическом стиле, в третьей философия сочеталась с математикой. В двух последних можно заметить влияние идей Вейгеля. В 1666 г. Лейбниц опубликовал «Диссертацию о комбинаторном искусстве», целью которой провозглашалась разработка логики открытия, и в которой высказывались идеи, что впоследствии получили развитие в комбинаторике и математической логике.

Поскольку Лейпцигский университет отказал Лейбницу в проведении защиты докторской диссертации (как слишком молодому), то ученый поехал в Нюрнберг, где его родственник, Ю.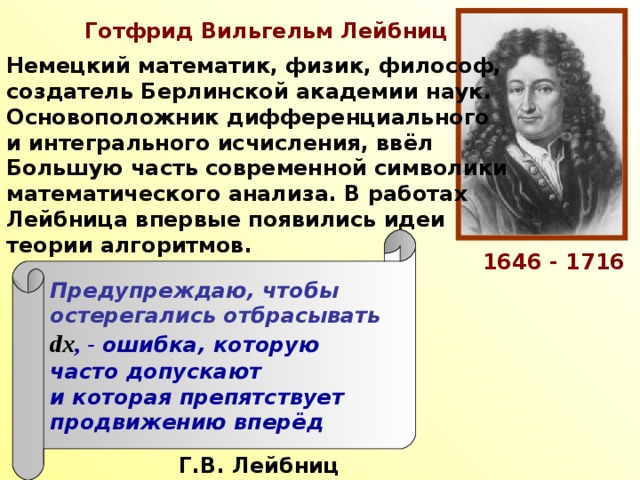 Я.Лейбниц, занимал высокий пост, и 5 ноября 1666 г. блестяще защитил докторскую диссертацию в Университете имперского города Нюрнберг , находившийся в г. Альтдорф вблизи Нюрнберга. В феврале 1667г. ему присудили степень доктора обоих прав (гражданского и церковного), а также предложили занять кафедру на юридическом факультете.

Майнц и Париж (1667-1676)

Лейбниц отклонил предложение о занятии кафедры и осенью 1667 г. поступил на службу Майнцскому курфюрсту Иоганну Филиппу фон Шенборну. Он стал помощником придворного советника Лассера, участвовал в подготовке нового свода законов. В 1668 г. он стал помощником бывшего министра Майнцского курфюрста Иоганна Христиана фон Бойнебурга и присоединился к международной политике. Лейбниц, в частности, написал меморандум, где обосновывались преимущества немецкого князя на польском престоле, который Бойнебург зачитал на польском сейме во время выборов короля. Лейбниц также работал над проблемой объединения христианских культов и церквей, которая беспокоила тех, кто хотел объединения Германии, которая тогда была раздроблена на несколько десятков государств. Он изучал много богословской литературы, надеясь разработать систему догматов, приемлемую и для католиков, и для протестантов различных течений.

В Майнце Лейбниц занялся исследованиями в области естествознания, написал работу, которая называлась «Новая физическая гипотеза» и состояла из двух частей — «Теория абстрактного движения» и «Теория конкретного движения». Начал работать над созданием механической счетной машины. Начал переписку с Лондонским королевским обществом, Парижской академией наук, отдельными учеными и философами.

Одной из актуальных проблем для Германии была военная угроза со стороны Франции. Чтобы отвести эту угрозу, Бойнебург и Лейбниц решили разработать для французского короля Людовика XIV проект завоевания Францией Египта. С этим проектом Лейбниц осенью 1672 г. уехал в Париж. Курфюрсту Шенборну о плане не сообщили.

В Париже Лейбниц прожил до конца 1676г. Это имело огромное значение для становления его как ученого и философа. Здесь он общался с мыслителями — философом и богословом А. Арно (одним из авторов знаменитого учебника по логике, известного как «Логика Пор-Рояля»), главой философов -картезианцев Н.Мальбраншем, знаменитым голландским физиком Х. Гюйгенса, в то время президентом Парижской академии наук. Здесь Лейбниц изучил французский, на котором впоследствии написал много трудов и писем, начал серьезно изучать математику и сделал свои первые математические открытия.

Осенью 1672 г. он поделился с Гюйгенсом результатами своих исследований, касающихся способа нахождения сумм определенных числовых рядов. Гюйгенс заметил, что Лейбниц не очень хорошо знает математику и посоветовал ему ознакомиться с «Геометрическим трудом» Григория с Сен-Винцента и «Арифметикой бесконечных» Дж. Валлиса — книгами, в которых в геометрической форме излагались элементы математического анализа.

В начале 1673 г. Лейбниц поехал в Лондон в составе дипломатической миссии Майнцского курфюрста. На заседании Лондонского королевского общества он сделал доклад о разработке механической счетной машины, которая должна была выполнять сложение, вычитание, умножение и деление, но еще не была готова. Доклад произвел хорошее впечатление, и после отъезда он был избран в члены Общества. Однако общение с математиками триумфа не принесло. Лейбниц узнал, что открытый им метод нахождения сумм рядов не новый, и вообще осознал свое, как впоследствии выразился, «высокомерное математическое невежество». Вернувшись в Париж, он, по совету Гюйгенса, изучает «Геометрию» Декарта, работы Б.Паскаля, в том числе неопубликованные, доступ к которым получил благодаря рекомендации А.Арно.

Осенью 1673 г. Гюйгенс подарил Лейбницу свою новую книгу «Маятниковые часы», которая содержала ряд его открытий в области математики и теоретической механики. Следующие три года Лейбниц посвятил главным образом математике. Он изучает математические труды, проводит исследования числовых рядов, алгебраических уравнений, поиска экстремумов и квадратур (площадей криволинейных фигур), обсуждает математические проблемы с Гюйгенсом и молодым немецким математиком Е.В.Чирнгаузом. От секретаря Лондонского королевского общества Ольденбурга он получает краткие сведения о некоторых результатах исследований И. Ньютона и английских математиков. Результатом этой работы стало то, что в середине 1676 г. Лейбниц сформулировал основные правила дифференцирования и интегрирования (см. «Лейбниц и математика» книги: Погребысский И.Б. «Готфрид Вильгельм Лейбниц»).

Ганновер (1676-1716)

В 1676 г. Лейбниц поступил на службу к герцогу Иоганну-Фридриху. Оставив Париж, он сначала поехал в Лондон, где продемонстрировал работу своей счетной машины. Затем побывал в Голландии, где встречался и имел длинные беседы с философом Б. Спинозой, изобретателем микроскопа А.Левенгуком, математиком Я.Гудде.

В декабре 1676 г. Лейбниц приехал в Ганновер, столицу Брауншвейг-Люнебурзького герцогства, и стал библиотекарем и придворным советником Иоганна-Фридриха, а через год — государственным чиновником при юридической канцелярии. Он предлагает совершенствования в различных областях государственного управления и производства, из которых попытались реализовать только проект использования ветровых двигателей совместно с водяными для откачки воды из шахт. В декабре 1679 г. Иоганн Фридрих умер, а его преемник, Эрнст Август, усовершенствованиями, как и библиотекой, интересовался мало. В 1685 г. он поручил Лейбницу написать историю своего княжеского дома (который был младшей ветвью рода Вельфов). Это стало основным занятием Лейбница на службе до последних дней жизни. Он отнесся к заданию творчески, решил, что следует писать не просто генеалогию одного рода, а общеисторическую работу, опираясь на первоисточники — хроники, воспоминания, указы и другие документы. С этой целью он планирует обзор архивов, и в 1688 г. едет в Вену, далее в Италию, где находился с марта 1689 г. по март 1690г. Там он собрал много ценных материалов, но они требовали осмысления и побуждали к новым поискам. Собственно, Лейбниц был первым, кто взялся за серьезную подготовительную работу по написанию истории Германии в Средние века и стал одним из первых историков, которые в своей работе использовали первоисточники и делали их критический обзор.

В то же время Лейбниц продолжает работать в области философии, математики, физики, логики. В 1682 г.. по его инициативе и при его активном участии в Лейпциге начал выходить научный журнал «Acta eruditorum». В 1684 г. он публикует свою первую статью по математическому анализу, в 1686 г. — статью о степени механического движения. Работает над философскими проблемами. Написал работы «Размышления о метафизике» (1686), «Новая система природы», «Новые исследования о человеческом разуме» (1704), «Теодицея» (1710), «Монадология» (1714) и др. Продолжал работать над проблемой объединения христианских церквей, ходатайствовал об учреждении обществ в Берлине, Дрездене и Вене, разработал проект академии наук для русского царя Петра I.

В 1698 г. ганноверский престол унаследовал сын Эрнста Августа — Георг-Людвиг, который не любил Лейбница, постоянно обвинял его в том, что он мало работает. Когда Георг-Людвиг в 1714 под именем Георга І стал английским королем, не захотел взять с собой в Лондон Лейбница, а велел ему оставаться в Ганновере и заканчивать историю Вельфов.

14 ноября 1716 г. Лейбниц умер в Ганновере.

Научное наследие Лейбница

Математика. Вместе с И. Ньютоном (и независимо от него) Лейбниц был основателем математического анализа — дифференциального и интегрального исчисления, причем сделал решающий вклад в создание этой области математики. Известны отдельные приемы решения задач на проведение касательных, поиска экстремумов, определение площадей криволинейных фигур Лейбниц свел в единую систему, исследовал основополагающие вопросы дифференциального и интегрального исчисления, предложил принятую сегодня символику и терминологию. Это он ввел обозначения dх, d2x, dy / dx, ∫ и др., Придумал термин «дифференциал», «дифференциальное исчисление», «интегральное исчисление», «дифференциальное уравнение», «функция», «переменная величина», «постоянная величина «,» координаты «,» абсцисса «,» алгебраические и трансцендентные кривые «и др. Лейбниц решил ряд знаменитых задач, в частности, о форме кривой наискорейшего спуска и цепной линии. Он переписывался с швейцарцами братьями Якобом и Иоганном Бернулли, французами П. Вариньоном и Г.Ф.Лопиталем, другими математиками, что способствовало стремительному развитию математического анализа в континентальной Европе. Получил Лейбниц и многие другие результаты, в частности, вывел ряд для числа π, описал двоичную систему счисления и предсказал перспективность ее применения в вычислительной технике.

В философию Лейбниц ввел разделение истин по происхождению на истины разума и истины факта. Критиковал распространенные в то время философские школы — картезианцев и сенсуалистов. Принцип сенсуалистов «Нет в уме ничего, чего бы не было в ощущениях», Лейбниц дополнил: «кроме самого разума». Если картезианцы единственным атрибутом материи считали протяженность (телесность) и рассматривали ее как пассивную субстанцию (откуда выводили закон инерции), то Лейбниц утверждал, что одной телесностью невозможно объяснить взаимодействие тел. По его представлениям, мир состоит из монад — единичных сущностей, обладающих внутренней активностью, в которых неразрывно связаны телесное и бестелесное (духовное), материя и движение.

В логике Лейбниц сформулировал закон достаточного основания, выдвинул идею математизации логики и построения логического исчисления. В механике Лейбниц, рядом с декартовским количеством движения (mv), ввел новую меру движения, «живую силу» (mv2), и сформулировал «закон сохранения живых сил», что стало шагом к закону сохранения энергии. Он развил теорию сопротивления балок сгибанию — ввел в расчеты закон Гука и момент инерции сечения балки. В геологии Лейбниц одним из первых высказал мысль об эволюции Земли и существования ее в прошлом в огненно-жидком состоянии. В биологию Лейбниц ввел идею целостности организмов — невозможности их сведения к совокупности механизмов. В психологии он выдвинул понятие бессознательных «малых перцепций» и развил учение о бессознательной психической жизни. В языкознании он выдвинул идею исторического происхождения языков, дал их генеалогическую классификацию, развил учение о происхождении названий.

В педагогике Лейбниц сформулировал принцип самостоятельности ученика, отмечал, что учитель должен научить ученика учиться и выработать у него потребность в постоянном пополнении знаний. Он критиковал положение Локка о человеческой душе как «чистой доске» (tabula rasa) и сравнивал душу ребенка с глыбой мрамора, красоту которой, скрытую в прожилках, может обнаружить мастер.

Лейбниц высказал также интересные идеи по организации образования, медицины, библиотечного дела, его называют одним из основателей эвристики.

Судьба научного наследия

При жизни Лейбниц опубликовал только одну большую философскую работу — «Теодицея» (Оправдание Бога), чем заслужил репутацию защитника религии. Вольтер высмеял оптимизм его философии в повести «Кандид, или Оптимизм». Англичане обвиняли Лейбница в том, что он украл метод математического анализа в Ньютона. В то же время Д. Дидро писал в «Энциклопедии», что Лейбниц для Германии был тем, кем для Греции были Платон, Аристотель и Архимед вместе взятые. Со временем, когда стали выходить в свет неопубликованные ранее работы, а также письма Лейбница, уважение к нему как мыслителю росло. Особенно высоко его стали уважать в ХХ веке. Б.Рассел высказался о Лейбница так: «Он был основателем математической логики, важность которой он понял еще тогда, когда она еще никому не была ясной». Н.Винер в книге «Кибернетика» написал: «Если бы мне пришлось выбирать в анналах истории наук святого — покровителя кибернетики, то я выбрал бы Лейбница».

Сегодня многие ученые исследуют научное наследие Лейбница, в частности его рукописи. Эти исследования привели недавно к удивительному открытию: нашли описание механической шифровальной машины Лейбница, по которому в 2014 году эту машину изготовили (см. Http://philsci-archive.pitt.edu/8499/ и http://blog.hnf.de / herr-leibniz-und-seine-chiffriermaschine /). В 2007 г.. Рукописи Лейбница, в том числе письма, включено в Всемирное наследие ЮНЕСКО. Проводится оцифровка его работ и рукописей, создано много сайтов, посвященных Лейбницу и его научному наследию. Думаю, со временем мы узнаем еще много нового о Лейбнице и его идеях.

В. Николаенко

Знакомство с Готфридом Лейбницем — сочинения Стивена Вольфрама.

Наука тоже — хотя на три столетия раньше. Поэтому, когда я недавно съездил в Германию, я был рад возможности посетить его архив в Ганновере.

Листая его пожелтевшие (но все еще достаточно крепкие, чтобы я мог потрогать) страницы его заметок, я почувствовал некую связь — поскольку пытался представить, о чем он думал, когда писал их, и пытался связать увиденное в них с что мы теперь знаем спустя еще три столетия:

Это эссе также находится в Создатели идей: личный взгляд на жизнь и идеи некоторых известных людей  »

Некоторые вещи, особенно в математике, совершенно вневременны. Например, вот Лейбниц записывает бесконечный ряд для √2 (текст на латыни):

Или вот Лейбниц пытается вычислить непрерывную дробь — хотя он ошибся в арифметике, хотя и записал все (Π была его более ранняя версия знака равенства):

Или вот небольшая сводка исчисления, которая почти могла бы быть в современном учебнике:

Но о чем все остальное? Какова была большая история его работы и размышлений?

Я всегда находил Лейбница несколько запутанной фигурой. Он занимался многими, казалось бы, разрозненными и не связанными между собой вещами — в философии, математике, теологии, праве, физике, истории и многом другом. И он описал то, что он делал, в терминах, которые сейчас кажутся нам странными для 17-го века.

Но по мере того, как я узнавал больше и лучше чувствовал Лейбница как личность, я понял, что под большей частью того, что он делал, скрывалось основное интеллектуальное направление, удивительно близкое к современному вычислительному направлению, которое я, для например, последовали.

Готфрид Лейбниц родился в Лейпциге на территории современной Германии в 1646 году (через четыре года после смерти Галилея и через четыре года после рождения Ньютона). Его отец был профессором философии; семья его матери занималась книжной торговлей. Отец Лейбница умер, когда Лейбницу было 6 лет, и после двухлетнего размышления о том, подходит ли она для такого молодого человека, Лейбниц был допущен в библиотеку своего отца и начал читать ее разнообразную коллекцию книг. В 15 лет он поступил в местный университет, изучая философию и право, и окончил оба факультета в 20 лет9.0007

Даже будучи подростком, Лейбниц, кажется, интересовался систематизацией и формализацией знаний. Долгое время существовали смутные идеи — например, в полумистическом Ars Magna Рамона Луллия 1300-х годов — что можно было бы создать некую универсальную систему, в которой все знания могли бы быть получены из комбинаций знаков, взятых из подходящего (как назвал его Декарт) «алфавита человеческой мысли». И в своей дипломной работе по философии Лейбниц пытался реализовать эту идею. Он использовал базовую комбинаторную математику для подсчета возможностей. Он говорил о разложении идей на простые компоненты, над которыми может работать «логика изобретения». И в довершение всего он привел аргумент, призванный доказать существование Бога.

Как позже сказал сам Лейбниц, этот тезис, написанный в возрасте 20 лет, был во многом наивен. Но я думаю, что это начало определять образ мыслей Лейбница на протяжении всей жизни обо всех вещах. Так, например, дипломная работа Лейбница по юриспруденции о «запутанных юридических делах» была посвящена потенциальному разрешению таких дел путем сведения их к логике и комбинаторике.

Лейбниц собирался стать профессором, но вместо этого решил начать жизнь, работая советником при различных дворах и политических правителях. Частью того, что он делал для них, была ученость, отслеживание малопонятных — но политически важных — генеалогии и истории. Отчасти это была организация и систематизация — сводов законов, библиотек и так далее. Частично это была практическая инженерия — например, попытка найти лучший способ не допустить попадания воды в серебряные рудники. И частично — особенно в ранние годы — это была интеллектуальная поддержка политических маневров «на местах».

Одно из таких занятий в 1672 году привело Лейбница в Париж на четыре года, в течение которых он общался со многими ведущими интеллектуалами. До этого знания Лейбница по математике были довольно базовыми. Но в Париже у него была возможность изучить все новейшие идеи и методы. И, например, он разыскал Христиана Гюйгенса, который согласился обучать Лейбница математике — после того, как ему удалось пройти испытание по нахождению суммы обратных величин треугольных чисел.

На протяжении многих лет Лейбниц совершенствовал свои идеи о систематизации и формализации знаний, представляя целую архитектуру того, как знание, говоря современным языком, могло бы стать вычислительным. Он видел первый шаг как развитие ars характеристика — методология присвоения вещам знаков или символических представлений и, по сути, создание единого «алфавита мысли». Затем он вообразил — в замечательном резонансе с тем, что мы сейчас знаем о вычислениях, — что из этого единообразного представления можно будет найти «истины разума в любой области… посредством исчисления, как в арифметике или алгебре».

Он говорил о своих идеях под множеством довольно амбициозных названий, таких как scientia generalis («общий метод познания»), linguaphilosophica («философский язык»), mathematique Universelle («всеобщая математика»), charactera universalis («универсальная система») и calculus ratiocinator («исчисление мысли»). В конечном счете, он представлял себе приложения во всех областях — науке, праве, медицине, инженерии, теологии и многих других. Но единственной областью, в которой он довольно быстро добился явного успеха, была математика.

Для меня удивительно, как редко в истории математики нотация рассматривалась как центральный вопрос. Это произошло на заре современной математической логики в конце 1800-х годов благодаря работам таких людей, как Готтлоб Фреге и Джузеппе Пеано. И в последнее время это случилось со мной в моих усилиях по созданию Mathematica и язык Wolfram. Но это также произошло три века назад с Лейбницем. И я подозреваю, что успехи Лейбница в математике в немалой степени были связаны с усилиями, которые он вложил в систему обозначений, и ясностью рассуждений о математических структурах и процессах, которые они привнесли.

Когда смотришь на работы Лейбница, интересно увидеть его обозначения и их развитие. Многие вещи выглядят вполне современно. Хотя есть очаровательные черточки 17-го века, вроде случайного использования алхимических или планетарных символов для алгебраических переменных:

В качестве знака равенства используется Π вместо =, с немного хакерской идеей, что это похоже на баланс, с более длинной ногой с одной или другой стороны, указывающей меньше («<») или больше («>» ):

Верхние черты указывают на группировку терминов — возможно, это лучшая идея, чем круглые скобки, хотя их труднее набирать и печатать:

Сегодня мы используем верхние черты для обозначения корней. Но Лейбниц хотел использовать их и в интегралах. Наряду с довольно симпатичным «хвостатым d», напоминающим мне «дифференциал d» с двойным штрихом, который мы изобрели для представления интегралов в Математика .

В частности, при решении уравнений довольно часто хочется использовать ±, и это всегда сбивает с толку, как должна работать группировка, скажем, в a ± b ± c . Что ж, Лейбниц, кажется, тоже находил это запутанным, но он изобрел обозначение для обработки этого, которое нам действительно следует использовать и сегодня:

Я не уверен, что означают некоторые из обозначений Лейбница. Хотя эти овертильды довольно симпатичные:

Как и эти вещи с точками:

Или эта интересная диаграммная форма:

Конечно, наиболее известными обозначениями Лейбница являются его интегральный знак (длинная «s» для «summa») и d, краткое изложение которого приведено здесь на полях для в первый раз, 11 ноября 1675 г. («5» в «1675 г. » заменено на «3» постфактум, возможно, Лейбницем):

Мне кажется интересным, что, несмотря на все его обозначения «вычислительных» операций , Лейбниц, по-видимому, не изобретал подобных обозначений для логических операций. «Или» было просто латинским словом или , «и» было и , и так далее. И когда он придумал кванторы (современные ∀ и ∃), он просто представил их латинскими сокращениями U.A. и P.A.:

Мне всегда казалось замечательной аномалией в истории мысли, что только в 1930-х годах появилась идея универсальных вычислений. И я часто задавался вопросом, не скрывается ли в трудах Лейбница ранняя версия универсальных вычислений — может быть, даже диаграмма, которую мы теперь могли бы интерпретировать как систему, подобную машине Тьюринга. Но по мере знакомства с Лейбницем мне стало яснее, почему это, вероятно, не так.

Один большой момент, я подозреваю, заключается в том, что он недостаточно серьезно относился к дискретным системам. Он называл результаты комбинаторики «самоочевидными», предположительно потому, что считал их поддающимися прямой проверке с помощью таких методов, как арифметика. И только «геометрическая», или непрерывная, математика, по его мнению, нуждалась в разработке исчисления для нее. Описывая такие вещи, как свойства кривых, Лейбниц придумал что-то вроде непрерывных функций. Но, похоже, он никогда не применял идею функций к дискретной математике, что, например, могло привести его к размышлениям об универсальных элементах для построения функций.

Лейбниц признал успех своего исчисления бесконечно малых и стремился придумать аналогичные «исчисления» для других вещей. И в другом «неудачном случае» с универсальными вычислениями у Лейбница возникла идея закодировать логические свойства с помощью чисел. Он думал о том, чтобы связать каждый возможный атрибут вещи с другим простым числом, затем охарактеризовать вещь произведением простых чисел ее атрибутов, а затем представить логический вывод с помощью арифметических операций. Но он рассматривал только статические атрибуты и никогда не приходил к такой идее, как гёделевская нумерация, где операции также кодируются числами.

Но хотя Лейбниц и не пришел к идее всеобщего вычисления, он понял, что вычисление в некотором смысле является механическим. И действительно, довольно рано он, похоже, решил построить настоящий механический калькулятор для выполнения арифметических операций. Возможно, отчасти это было потому, что он хотел использовать его сам (всегда веская причина для создания технологии!). Ибо, несмотря на его мастерство в алгебре и тому подобном, его статьи очаровательно полны основных (и иногда неправильных) арифметических вычислений школьного уровня, написанных на полях — и теперь сохраненных для потомков:

Были разрозненные образцы механических калькуляторов, построенных во времена Лейбница, и, когда он был в Париже, Лейбниц, несомненно, видел калькулятор сложения, который был построен Блезом Паскалем в 1642 году. Но Лейбниц решил создать «универсальный» калькулятор, который впервые мог выполнять все четыре основные арифметические функции с помощью одной машины. И он хотел дать ему простой «пользовательский интерфейс», где можно было бы, например, повернуть ручку в одну сторону для умножения и в другую — для деления.

В бумагах Лейбница есть всевозможные схемы того, как должна работать машина:

Лейбниц воображал, что его калькулятор будет иметь большую практическую пользу, и действительно, кажется, он надеялся, что сможет превратить его в успешную бизнес. Но на практике Лейбниц изо всех сил пытался заставить калькулятор работать вообще надежно. Как и другие механические калькуляторы того времени, это был прославленный одометр. И точно так же, как и в машинах Чарльза Бэббиджа почти 200 лет спустя, было механически трудно заставить двигаться сразу несколько колес, когда возникал каскад переносов.

Сначала Лейбниц построил деревянный прототип своей машины, предназначенный для обработки только 3 или 4 цифр. Но когда он продемонстрировал это таким людям, как Роберт Гук, во время визита в Лондон в 1673 году, все прошло не очень хорошо. Но он продолжал думать, что со всем разобрался — например, в 1679 г. написал (по-французски) «последнюю поправку к арифметической машине»:

Заметки 1682 г. предполагают, однако, что проблем было больше:

Но Лейбниц имел планы, составленные из его заметок, и нанял инженера для создания латунной версии с большим количеством цифр:

Забавно посмотреть «маркетинговый материал» Лейбница для машины:

А также части «руководства» (с 365×24 в качестве «рабочего примера»):

В комплекте с подробными схемами использования:

Но несмотря на все эти усилия, проблемы с калькулятором продолжались. И действительно, более 40 лет Лейбниц продолжал настраивать свой калькулятор, потратив, вероятно, в общей сложности (в сегодняшней валюте) на него более миллиона долларов.

Так что же на самом деле случилось с физическим калькулятором? Когда я посетил архив Лейбница, мне пришлось спросить. «Ну, — сказали мои хозяева, — мы можем показать вам». А там, в подвале, вместе с полками с коробками, стоял калькулятор Лейбница, выглядевший как новый в стеклянном футляре, — здесь запечатленный мною в странном сопоставлении древности и современности:

Все детали на месте. Включая удобный деревянный ящик для переноски. В комплекте с поворотной ручкой. И, если он работал правильно, возможность выполнить любую базовую арифметическую операцию за несколько минут прокрутки:

Лейбниц явно рассматривал свой калькулятор как практический проект. Но он все еще хотел обобщить ее, например, пытаясь создать общую «логику» для описания геометрии механических связей. И он также думал о природе чисел и арифметики. И особенно поразили двоичные числа.

Основания, отличные от 10, использовались в развлекательной математике на протяжении нескольких столетий. Но Лейбниц ухватился за основание 2 как имеющее особое значение и, возможно, являющееся ключевым мостом между философией, теологией и математикой. И в этом его воодушевляло осознание того, что двоичные числа лежат в основе И Цзин , о которых он слышал от миссионеров в Китае и которые рассматривал как связанные по духу с его характеристикой универсальной .

Лейбниц выяснил, что можно построить калькулятор на основе двоичного кода. Но он, кажется, думал, что только 10-кратное основание может быть действительно полезным.

Странно читать то, что Лейбниц писал о двоичных числах. Некоторые из них ясны и практичны — и до сих пор кажутся совершенно современными. Но некоторые из них относятся к 17 веку — например, речь идет о том, как бинарность доказывает, что все может быть сделано из ничего, где 1 отождествляется с Богом, а 0 — с ничем.

Почти ничего не делалось с двоичным кодом в течение нескольких столетий после Лейбница: фактически, до появления цифровых вычислений в последние несколько десятилетий. Поэтому, если взглянуть на работы Лейбница, его вычисления в двоичной системе, вероятно, кажутся наиболее «несвоевременными»:

С помощью двоичной системы Лейбниц в некотором смысле искал простейшую возможную базовую структуру. И, без сомнения, он делал нечто подобное, когда говорил о том, что он называл «монадами». Должен сказать, что я никогда по-настоящему не понимал монады. И обычно, когда я думаю, что почти понял, какое-то упоминание о душах просто сбивает меня с толку.

Тем не менее, меня всегда мучил вывод Лейбница о том, что «лучшим из всех возможных миров» является тот, «имеющий наибольшее разнообразие явлений из наименьшего числа принципов». И действительно, в предыстории моей работы на Новый вид науки , когда я впервые начал формулировать и изучать одномерные клеточные автоматы в 1981 году, я подумывал назвать их «полимонами», но в последнюю минуту струсил, когда снова запутался в монадах.

Вокруг Лейбница и его документов всегда была некая мистика. Курт Гёдель — возможно, демонстрируя свою паранойю — казался убежденным, что Лейбниц открыл великие истины, которые веками скрывались. Но хотя документы Лейбница и были запечатаны после его смерти, беспокойство вызывали его работы по таким темам, как история и генеалогия, а также связанные с ними государственные секреты.

Документы Лейбница были давно распечатаны, и по прошествии трех столетий можно предположить, что каждый их аспект был бы хорошо изучен. Но дело в том, что даже по прошествии стольких лет никто так подробно и не изучил все бумаги. Дело не в том, что их так много. Всего там всего около 200 000 страниц, что занимает примерно дюжину полок (и лишь немногим больше, чем мой личный архив только 1980-х годов). Но проблема в разнообразии материала. Не только множество предметов. А также множество накладывающихся друг на друга черновиков, заметок и писем с неясными отношениями между ними.

Архив Лейбница содержит огромное количество документов. От очень большого:

До очень маленького (почерк Лейбница становился все меньше по мере того, как он становился старше и близоручее):

Большинство документов в архиве кажутся очень серьезными и прилежными. Но, несмотря на высокую стоимость бумаги во времена Лейбница, до сих пор сохранились для потомков случайные каракули (это случайно не Спиноза?):

над Европой. Так что сейчас, 300 лет спустя, в его архиве можно найти «случайные письма» от таких, как Яков Бернулли:

Как выглядел Лейбниц? Вот он, как на официальном портрете, так и без довольно большого парика (над которым даже в его время насмехались), который он, предположительно, носил, чтобы прикрыть большую кисту на голове:

Как человек, Лейбниц, кажется, был вежлив, обходителен и даже сдержан. В каком-то смысле он мог показаться ботаником, глубоко рассуждающим на всевозможные темы. Похоже, он прилагал огромные усилия — как и в своих письмах — приспосабливаться к тому, с кем разговаривал, подчеркивая теологию, когда разговаривал с теологом, и так далее. Как и многие интеллектуалы его времени, Лейбниц никогда не был женат, хотя, кажется, он пользовался некоторым успехом у придворных женщин.

В своей карьере придворного Лейбниц стремился подняться по карьерной лестнице. Но не увлекаясь охотой и пьянством, он никогда не вписывался во внутренние круги правителей, на которых работал. В конце своей жизни, когда Георг I Ганноверский стал королем Англии, для Лейбница было естественным присоединиться к его двору. Но Лейбницу сказали, что прежде чем он сможет уйти, он должен начать писать исторический проект, над которым он якобы работал 30 лет. Если бы он сделал это перед смертью, он вполне мог бы отправиться в Англию и общаться с Ньютоном совсем по-другому.

В архиве Лейбница есть много бумаг, его механический калькулятор и еще одна вещь: складной стул, который он брал с собой в путешествия и который он подвешивал в вагонах, чтобы продолжать писать во время движения вагона. :

Лейбниц очень беспокоился о статусе (он часто называл себя «Готфридом фон Лейбницем», хотя никто точно не знал, откуда взялось это «фон»). И в знак признания своих открытий он хотел создать медаль в память о двоичных числах. Он разработал подробный дизайн с лозунгом 9.0003 omnibus ex nihilo ducendis; sufficit unum («все может быть получено из ничего; все, что нужно, это 1»). Но никто никогда не делал медаль для него.

В 2007 году, однако, я хотел придумать подарок на 60-летие для моего друга Грега Чайтина, который был давним энтузиастом Лейбница. И вот я подумал: а почему бы вообще не сделать медаль Лейбница? Так мы и сделали. Правда, на обороте вместо изображения герцога, которое предлагал Лейбниц, мы поставили латинскую надпись о работе Грега.

И когда я посетил архив Лейбница, я обязательно принес копию медали, чтобы, наконец, поставить настоящую медаль рядом с рисунком Лейбница:

Было бы интересно узнать, какое содержательное заявление могло быть у Лейбница на его могиле. Но как бы то ни было, когда Лейбниц умер в возрасте 70 лет, его политическая судьба пошла на убыль, и не было сооружено сложного мемориала. Тем не менее, когда я был в Ганновере, мне очень хотелось увидеть его могилу, на которой, как оказалось, была простая латинская надпись «кости Лейбница»:

Однако на другом конце города есть еще одно своеобразное памятное место — магазин печенья, названного в его честь «Лейбниц»:

Так что же нам делать с Лейбницем в конце концов? Если бы история развивалась иначе, то, вероятно, существовала бы прямая связь от Лейбница к современным вычислениям. Но как бы то ни было, многое из того, что пытался сделать Лейбниц, стоит особняком — его можно понять, главным образом, проецируя назад от современного вычислительного мышления к 17 веку.

А из того, что мы знаем сейчас, достаточно ясно, что понимал Лейбниц, а что нет. Он понял концепцию наличия формальных, символических представлений для широкого круга различных вещей. И он подозревал, что могут существовать универсальные элементы (может быть, даже просто 0 и 1), из которых можно построить эти представления. И он понял, что из формального символического представления знания можно механически вычислить его последствия и, возможно, создать новое знание путем перечисления возможностей.

Кое-что из того, что писал Лейбниц, было абстрактным и философским, иногда сводящим с ума. Но на каком-то уровне Лейбниц был также весьма практичен. И он обладал достаточным техническим мастерством, чтобы часто добиваться реального прогресса. Его типичный подход, по-видимому, заключался в том, чтобы начать с попытки создать формальную структуру для прояснения вещей — с формальной нотацией, если это возможно. И после этого его целью было создать своего рода «исчисление», из которого можно было бы систематически делать выводы.

На самом деле он добился настоящего успеха только в одной конкретной области: непрерывной «геометрической» математике. Жаль, что он никогда более серьезно не занимался дискретной математикой, потому что я думаю, что он мог бы добиться прогресса и, возможно, даже прийти к идее универсальных вычислений. Вполне возможно, что он также начал бы перечислять возможные системы, как это сделал я в вычислительной вселенной.

Одной из областей, где он попробовал свой подход, была юриспруденция. Но в этом он, конечно, был слишком рано, и только теперь — 300 лет спустя — вычислительный закон начинает казаться реалистичным.

Лейбниц тоже пытался думать о физике. Но хотя он продвинулся в некоторых конкретных понятиях (таких как кинетическая энергия), ему так и не удалось придумать какую-либо крупномасштабную «систему мира», подобную той, что Ньютон фактически сделал в своих Principia .

В некотором смысле, я думаю, что Лейбницу не удалось добиться большего прогресса, потому что он слишком старался быть практичным и, подобно Ньютону, расшифровывать действие реальной физики, а не просто рассматривать связанные формальные структуры. Ибо если бы Лейбниц попытался провести хотя бы основные виды исследований, которые я сделал в Новый вид науки , я не думаю, что у него были бы технические трудности, но я думаю, что история науки могла бы быть совсем другой.

И я пришел к выводу, что, когда Ньютон выиграл пиар-войну против Лейбница за изобретение исчисления, на карту была поставлена ​​не только репутация; это был способ думать о науке. Ньютон был в некотором смысле типичным практиком: он изобрел инструменты, а затем показал, как их можно использовать для получения практических результатов о физическом мире. Но у Лейбница был более широкий и философский взгляд, и он рассматривал исчисление не только как специфический инструмент сам по себе, но и как пример, который должен вдохновлять усилия на другие виды формализации и другие виды универсальных инструментов.

Я часто думал, что современный вычислительный способ мышления, которому я следую, в какой-то степени очевиден и в какой-то степени неизбежен при формальном, структурированном мышлении о вещах. Но мне никогда не было ясно, является ли эта кажущаяся очевидность просто результатом современности и нашего опыта работы с современными практическими компьютерными технологиями. Но глядя на Лейбница, мы получаем некоторую перспективу. И действительно, мы видим, что некое ядро ​​современного вычислительного мышления было возможно даже задолго до Нового времени. Но окружающие технологии и понимание прошлых веков наложили определенные ограничения на то, насколько далеко может зайти мышление.

И, конечно же, это приводит к отрезвляющему вопросу для нас сегодня: сколько мы не можем понять из основного вычислительного способа мышления, потому что у нас нет окружающей технологии далекого будущего? Для меня, глядя на Лейбница, этот вопрос стал более четким. И по крайней мере одна вещь кажется достаточно ясной.

За всю жизнь Лейбниц, по сути, видел меньше нескольких компьютеров, и все, что они делали, — это элементарная арифметика. Сегодня в мире миллиарды компьютеров, и они делают самые разные вещи. Но в будущем наверняка будет гораздо больше компьютеров (их будет легче создавать благодаря Принципу вычислительной эквивалентности). И, без сомнения, мы придем к тому, что практически все, что мы делаем, будет явно состоять из компьютеров на всех уровнях. И в результате получится программировать абсолютно все, вплоть до атомов. Конечно, биология в некотором смысле уже достигла ограниченной версии этого. Но мы сможем сделать это полностью и везде.

На каком-то уровне мы уже можем видеть, что это подразумевает некое слияние вычислительных и физических процессов. Но почему нам может быть так же трудно представить себе, как Лейбницу представляли такие вещи, как Mathematica и Wolfram|Alpha.

Лейбниц умер 14 ноября 1716 года. В 2016 году это будет 300 лет назад. И это будет хорошая возможность убедиться, что все, что у нас есть от Лейбница, наконец-то реализовано — и отпраздновать спустя три столетия, как многие аспекты основного видения Лейбница, наконец, воплощаются в жизнь, хотя и так, как он никогда не мог себе представить.

Готфрид Вильгельм Лейбниц – Истинный отец исчисления?

Биография

Готфрид Лейбнис (1646-1716)

. Он был, наряду с Рене Декартом и Барухом Спинозой, одним из трех великих рационалистов 17-го века, и его работа предвосхитила современную логику и аналитическую философию. Как и многие великие мыслители до и после него, Лейбниц был вундеркиндом и внес свой вклад во многие области деятельности.

Но между работой над философией и логикой и основной работой в качестве политика и представителя королевского дома Ганновера Лейбниц все же находил время для занятий математикой. Возможно, он был первым, кто явно использовал математическое понятие функции для обозначения геометрических понятий, полученных из кривой, и разработал систему исчисления бесконечно малых независимо от своего современника сэра Исаака Ньютона. Он также возродил древний метод решения уравнений с использованием матриц, изобрел практичную вычислительную машину и впервые применил двоичную систему.

Как и Ньютон, Лейбниц был членом Королевского общества в Лондоне и почти наверняка знал о работах Ньютона по математическому анализу. В 1670-х годах (немного позже, чем ранние работы Ньютона) Лейбниц разработал очень похожую теорию исчисления, по-видимому, совершенно независимо. В течение короткого периода, около двух месяцев, он разработал полную теорию дифференциального исчисления и интегрального исчисления (см. раздел о Ньютоне для краткого описания и объяснения развития исчисления).

Leibniz’s and Newton’s notation for Calculus

Unlike Newton, however, he was more than happy to publish his work, and so Europe first heard about calculus from Leibniz in 1684, and не от Ньютона (который ничего не публиковал по этому вопросу до 1693 г.). Когда Королевскому обществу было предложено вынести решение между соперничающими претензиями двух мужчин по поводу развития теории исчисления, они приписали первое открытие Ньютону, а первую публикацию — Лейбницу. Однако Королевское общество, находившееся к тому времени под довольно предвзятым председательством самого Ньютона, позже также обвинило Лейбница в плагиате, оскорбление, от которого Лейбниц так и не оправился.

По иронии судьбы именно математика Лейбница в конце концов восторжествовала, и его обозначения и его способ записи исчисления, а не более неуклюжие обозначения Ньютона, до сих пор используются в математике.

Помимо исчисления, Лейбниц заново открыл метод упорядочивания линейных уравнений в виде массива, теперь называемого матрицей, которым затем можно было манипулировать для поиска решения. Подобный метод впервые был предложен китайскими математиками почти двумя тысячелетиями ранее, но давно вышел из употребления. Лейбниц проложил путь для более поздних работ Карла Фридриха Гаусса по матрицам и линейной алгебре. Он также ввел понятия самоподобия и принципа непрерывности, которые предвосхитили область математики, которая впоследствии стала называться топологией.

Бинарные номера Система

Двоичные численные системы

, которая использовалась, и была использована на основе, которая была использована на салоне, и использовалась на основе.