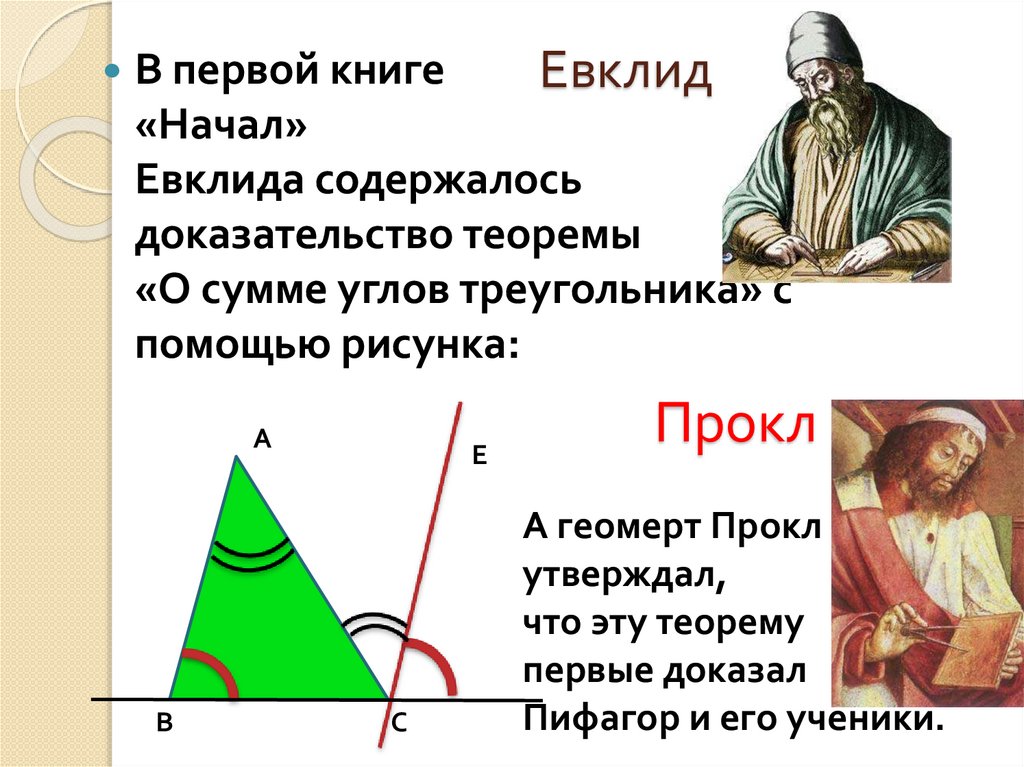
14. ЕВКЛИД (Сведения о нем известны с 300 г. до н. э.). 100 великих людей

14. ЕВКЛИД (Сведения о нем известны с 300 г. до н. э.)

Только несколько человек из нашего списка могут претендовать на такую же неувядаемую славу, как великий греческий геометр Евклид. Хотя при жизни такие личности, как Наполеон, Александр Великий и Мартин Лютер, были более известны, чем Евклид, с течением времени его слава, вероятно, переживет их славу. Несмотря на популярность Евклида, не известны никакие подробности о его жизни. Мы знаем, что он был учителем Александра в Египте примерно в 300 году до н. э. Однако даты его рождения и смерти неточны, и неизвестно даже, на каком континенте он родился, не говоря уже о городе. Хотя он является автором нескольких книг, некоторые из которых сохранились до сих пор, его место в истории прочно остается за ним благодаря, главным образом, одной книге — знаменитому учебнику по геометрии «Начала».

Значение «Начал» определяется не какой-то одной отдельно взятой теоремой из тех, которые здесь предложены. Почти все теоремы, включенные в эту книгу, были хорошо известны до Евклида, точно так же, как и многие доказательства. Огромной заслугой Евклида является систематизация материала и разработанный им общий план книги. Эта работа заключалась, прежде всего, в выборе необходимого набора аксиом и постулатов. (Это была очень трудная задача, требующая от составителя нестандартной оценки и огромной проницательности.) Затем он произвел тщательную систематизацию теорем, при которой каждая теорема логически вытекала из предыдущей. Если было необходимо, он добавлял отсутствующие фрагменты и разрабатывал отсутствующие доказательства. «Начала», давая, главным образом, основы планиметрии и стереометрии, содержит также большие разделы по алгебре и теории чисел, что не представляет, однако, особого интереса.

«Начала» служат в качестве учебника уже более двух тысяч лет, и это, безусловно, учебник с самой счастливой судьбой из всех написанных до сих пор.

Евклид так превосходно выполнил свою работу, что с появлением этой книги все ранее написанные учебники по геометрии были ею с успехом заменены и вскоре забыты. Написанные на греческом языке, «Начала» были впоследствии переведены на многие другие языки. Первое печатное издание появилось в 1482 году, спустя всего лишь три года после изобретения Гутенбергом книгопечатания. С тех пор было опубликовано более тысячи различных изданий. Являясь средством тренировки человеческого ума в области логического мышления, «Начала» значили больше, чем любой из трактатов Аристотеля по логике. Эта книга — выдающийся пример законченной дедуктивной структуры, которая с момента своего создания не перестает восхищать мыслителей. Справедливости ради следует отметить, что книга Евклида явилась главным фактором в развитии современной науки. Наука — это большее, чем простое собрание точных наблюдений и тонких обобщений. Современная наука добилась замечательных успехов в результате сочетания эмпиризма и экспериментирования, с одной стороны, и тщательного исследования и дедуктивного умозаключения — с другой. Мы не знаем точно, почему наука зародилась раньше в Европе, а не в Китае или Японии, но можно вполне уверенно сказать, что это неслучайно. Безусловно, огромную роль в этом сыграли такие блестящие личности, как Ньютон, Галилео Галилей, Коперник и Кеплер. Однако вполне вероятно, что были свои причины на то, почему подобные им люди процветали в Европе, а не на Востоке. Вероятно, самым решающим историческим фактором, повлиявшим на предрасположенность Западной Европы к развитию науки, был греческий рационализм параллельно с математическими знаниями, которые завещали греки.

Для европейцев представление о том, что существует несколько физических принципов, из которых можно вывести все остальное, было вполне естественным потому, что они имели перед собой пример Евклида. (Европейцы, в основном, не рассматривали геометрию Евклида как абстрактную систему. Они считали, что постулаты Евклида, а следовательно, и его теоремы, по сути дела, отражали реальную действительность.)

Все вышеупомянутые люди были буквально пропитаны евклидовскими традициями. И на самом деле, они тщательно изучали «Начала» и на их базе формировали основу своих математических знаний. Влияние Евклида на Исаака Ньютона бы по более чем очевидным, потому что Ньютон написал свою великую книгу «Математические начала натуральной философии» в «геометрической» форме, подобной той, в которой были написаны «Начала». С тех пор многие другие западные ученые следовали примеру Евклида и демонстрировали, как, оттолкнувшись от нескольких первоначальных предположений, путем логических рассуждений можно перейти к конкретным выводам. Так поступали многие математики, такие как Бертран Рассел и Альфред Норт Уайтхед, а также философы, такие как Спиноза.

Контраст с Китаем вызывает особое изумление. Столетиями техника развивалась там быстрее, чем в Европе. Но никогда в Китае не существовало математиков, подобных Евклиду, и, соответственно, Китай никогда не обладал теоретической математической базой, какая была у Запада. (Китайцы хорошо знали практическую геометрию, но их геометрические знания никогда не преобразовывались в дедуктивные схемы). Евклид не был переведен в Китае до 1600 года н. э., и прошло несколько столетий, прежде чем его концепция дедуктивных схем геометрии стала популярной у образованных китайцев. Пока этого не произошло, у китайцев не было серьезных работ в области науки. То же самое можно сказать о Японии, где труд Евклида не был известен до XVIII столетия, и даже и после этого не был оценен по достоинству. Хотя в Японии сегодня много превосходных ученых, там не было ни одного выдающегося ученого до тех пор, пока там не стал известен Евклид. Только и остается задумываться о том, смогли бы европейцы создать современную науку, если бы Евклид не проторил им дорогу!

Сегодня математики поняли, что геометрия Евклида является не единственной последовательной геометрической системой, и за прошедшие 150 лет было создано много неевклидовых геометрий. И, по сути дела, с тех пор, как в мире признали теорию относительности Эйнштейна, ученые пришли к выводу, что геометрия Евклида не всегда бывает точной в условиях истинной Вселенной. Например, в непосредственной близости от черных дыр и нейтронных звезд, где создаются чрезвычайно мощные гравитационные поля, евклидова геометрия не дает точной картины мира. Однако это довольно специфические случаи; в большинстве же случаев евклидова геометрия дает очень близкое приближение к реальности. Эти последние достижения в области человеческих знаний ни в коей мере не умаляют интеллектуального вклада Евклида. Ни в коей мере они не умаляют его роли в развитии математики и в создании логической структуры, необходимой для развития науки.

Данный текст является ознакомительным фрагментом.

Как Евклид доказал существование бесконечного количества простых чисел?

Как Евклид доказал существование бесконечного количества простых чисел? Древнегреческий математик Евклид (III век до нашей эры), более известный своей геометрией, доказал также одно из фундаментальных положений теории чисел – бесконечность количества простых чисел.

При

7. ЦАЙ ЛУНЬ (сведения о его жизни известны с 105 г.)

7. ЦАЙ ЛУНЬ (сведения о его жизни известны с 105 г.) Цай Лунь, изобретатель бумаги, — человек, чье имя, наверное, незнакомо большинству читателей. Если говорить о важности его изобретения, вызывает крайнее изумление тот факт, что его имя почти полностью игнорируется в

15. МОИСЕЙ (Сведения о нем известны с XIII века до н. э.)

15. МОИСЕЙ (Сведения о нем известны с XIII века до н. э.) Вероятно, ни один человек в истории не был отмечен такой всеобщей любовью, как великий древнееврейский пророе Моисей. К тому же с течением времени его слава только возрастает, как и число его почитателей. Вероятнее всего,

14. ЕВКЛИД «НАЧАЛА»

14.  ЕВКЛИД «НАЧАЛА» Евклид, пожалуй, единственный великий ученый, который ни при жизни, ни после смерти не подвергался критике, травле или инсинуациям. Он одинаково чтился представителями любых, даже самых непримиримых между собой направлений — ив математике, и в

ЕВКЛИД

ЕВКЛИД (ок. 365–300 до н. э.)О жизни этого учёного почти ничего не известно. До нас дошли только отдельные легенды о нём. Первый комментатор «Начал» Прокл (V век нашей эры) не мог указать, где и когда родился и умер Евклид. По Проклу, «этот учёный муж» жил в эпоху царствования

Евклид

Евклид (рубеж IV – III вв. до н.э.) математик, работал в Александрии То, что принято без доказательств, может быть отвергнуто без доказательств.[1018]Нет царского пути в геометрии. (Ответ Евклида египетскому царю Птолемею I, просившему указать ему более легкий путь изучения

Евклид

ЕВКЛИД (рубеж IV–III вв.

до н. э.),

ЕВКЛИД (рубеж IV–III вв. до н. э.), древнегреческий математик, работал в Александрии 7 Что и требовалось доказать. «Элементы геометрии» (ок. 300 г. до н. э.) Слова, помещаемые в конце доказательства теоремы. В латинской версии: «Quod erat demonstrandum» (перевод венецианца Бартоломео

ЕВКЛИД

ЕВКЛИД (рубеж IV–III вв. до н. э.),древнегреческий математик, работал в Александрии1Нет царского пути в геометрии (математике).Ответ египетскому царю Птолемею I, который просил указать ему более легкий путь изучения геометрии.Высказывание приведено в «Математической

Сведения об авторах

Сведения об авторах ФЕСЬКОВ Виталий ИвановичВ 1979 г. окончил Кемеровское высшее военное командное училище связи. В период 1975–1999 гг. проходил воинскую службу в Советской (Российской) Армии. Подполковник запаса, ветеран боевых действий в Афганистане.Председатель

Общие сведения

Общие сведения Происхождение и биологические особенности домашней птицы Одомашнена курица была древними персами; в странах Европы домашняя курица появилась за 500 лет до н. э. В конце XVIII века курица стала занимать первое место в мировом птицеводстве.Все породы кур имеют

Общие сведения

Общие сведения Внешний видСтати утки представлены на рисунке.Голова мясных пород уток (пекинские) длинная, со слегка приподнятым широким лбом. В отличие от сухопутных птиц, клюв у них не трехгранный, а плоский и длинный, с небольшим загибом в конце. По его краям

Общие сведения

Общие сведения Внешний видИз всех существующих ныне домашних птиц гуси были одомашнены первыми. Стати гуся представлены на рисунке.Голова у гусей по форме бывает различной. Сильно сдавленная голова с боков, с удлиненным клювом нежелательна.Клюв может быть прямой,

Общие сведения

Общие сведения Внешний видИндеек разводят почти на всех континентах земного шара.Это стройная, длинноногая птица с короткими крыльями и хвостом. Индейки имеют большую живую массу, крепкие ноги, мощные крылья. Голова и верхняя часть шеи голые. Ноги красные. На голове у нее

А. Общие сведения

А. Общие сведения 1. Очистка стальных деталей от ржавчины должна произво­диться в ингибированной соляной кислоте, представляющей смесь соляной кислоты (уд. вес 1,18) с ингибитором марки ПБ-5 (0,8—1% по отношению к объему соляной кислоты).Ингибированная соляная кислота хорошо

ЕВКЛИД

ЕВКЛИД То, что принято без доказательств, может быть отвергнуто без доказательств. Фрагменты (185, с.427) Нет царского пути в геометрии. (Ответ Евклида египетскому царю Птолемею I, просившему указать ему более легкий путь изучения геометрии.) (Прокл. «Схолии к Эвклиду») (185,

Евклид и его вклад в геометрию

Всем известно, что наука не вчера была изобретена – еще в древние времена выдающиеся умы открывали различные теоремы, теории, создавали новые элементы. Особым почетом пользовалась математика и астрономия. В этих науках преуспели греки и египтяне.

Сейчас невозможно представить себе математику без теоремы Пифагора, без знаменитого открытия Архимеда в ванной. Был еще один грек, который внес ощутимый вклад в науку в целом. Его имя – Евклид.

Евклид (325 г. до н. э. – 265 г. до н. э.) – греческий математик. Он считается «отцом геометрии». Его учебник «Элементы» оставался весьма востребованным и точным пособием по математике до конца 19-го века и является одним из наиболее широко опубликованных книг в мире. Но что же можно сказать про самого автора? К сожалению, немного. Сведения о его жизни крайне скудны и зачастую неправдоподобны.

Содержание

Биография Евклида

Евклид родился в середине 4-го века до нашей эры и жил в Александрии, на территории Египта; пик его творческой деятельности пришелся на время правления Птолемея I (323-283 до н.э), а его имя Евклид означает «известный, славный». В некоторых источниках он также упоминается, как Евклид Александрийский.

Вероятно, Евклид работал с командой математиков в Александрии, и он получил степень при помощи его математических работ. Некоторые историки считают, что работы Евклида, возможно, были результатом нескольких авторов, но большинство согласны с тем, что один человек – Евклид – был главным автором.

Вполне вероятно, что Евклид учился в Академии Платона в Афинах, и большая часть его знаний пришла оттуда. Именно там он впервые познакомился с математикой, а именно с одной ее частью – геометрией.

Современники описывали его, как доброго, приятного в общении человека. Например, историк Папп пишет, что Евклид был

«.. наиболее справедливым и благожелательным по отношению ко всем, кто смог в какой-либо мере продвинуть математику. Он осторожно отзывался, чтобы никоим образом не причинить обиду. И хотя он был великим ученым, никогда не хвастался сам».

О личной жизни математика неизвестно – почти все время он посвящал науке.

Постулаты Евклида

Его главная книга «Элементы» (первоначально написанная на древнегреческом языке) стала базовой работой важных математических учений. Она разделена на 13 отдельных книг.

• Книги от первой до шестой посвящены геометрии плоскости.
• Книги семь-девять имеют дело с теорией чисел
• Книга восьмая о геометрической прогрессии
• Книга десятая посвящена иррациональным числам
• Книги одиннадцать-тринадцать представляют собой трехмерную геометрию (стереометрию).

Гений Евклида состоял в том, чтобы взять в оборот множество разнообразных элементов математических идей и объединить их в один логический, последовательный формат.

Лемма Евклида, которая утверждает, что фундаментальное свойство простых чисел состоит в том, что если простое число делит произведение двух чисел, оно должно делить по крайней мере одно из этих чисел.

Алгоритм Евклида

Используя лемму Евклида, эта теорема утверждает, что каждое целое число больше единицы либо само по себе простое число, либо произведение простых чисел и что существует определенный порядок простых чисел.

«Если два числа, умножая одно на другое, составляют некоторое число, и любое число, которое делится на их произведение, также будет делиться на каждое из исходных чисел».

Евклидов алгоритм — эффективный метод вычисления наибольшего общего делителя (НОД) двух чисел, наибольшего числа, которое делит их оба, не оставляя остатка.

Геометрия Евклида

Евклид описал систему геометрии, связанную с формой, относительным положением и свойствами пространства. Его работа известна как евклидова геометрия. Предполагается, что пространство имеет размерность, равную трем.

Иногда его труд «Элементы» сравнивают с Библией – в том смысле, что его работа переведена на множество языков и в прямом смысле стала настольной книгой многих ученых и математиков последующих веков.

Помимо геометрии, Евклид исследовал и другие отрасли математики. Однако стоит признать, что вклад Евклида в науку огромен – без него, наверно, математика не смогла бы настолько раскрыться перед учеными. Его имя неразрывно связано с геометрией, изучением пространства.

Биография Евклида — факты, детство, семейная жизнь и достижения Цитаты Евклида Математики

место смерти: Александрия, Египет

Рекомендуется для вас

Детство и молодость

О Евклиде имеется очень мало информации, но предполагается, что он родился около 330 г. до н.э. в Тире. Судя по сообщениям некоторых арабских авторов, он происходил из богатой среды. Его отцом был Навкрат, а дедом — Зенарх.

Говорят, что он был греком, родился в Тире и всю свою жизнь жил в Дамаске. Однако нет определенных доказательств того, что он был тем же человеком, что и Евклида Александрийского, которого часто путают с Евклидом Мегарским, другим человеком, который был философом и жил во времена Платона.

Поскольку отсутствие биографических сведений довольно необычно для этого периода, многие исследователи полагают, что Евклида, возможно, вообще не существовало, а на самом деле его работы могли быть написаны группой математиков, взявших себе имя Евклид. Но эта гипотеза снова отвергается учеными, ссылаясь на отсутствие веских доказательств.

Говорят также, что он учился в древней школе Платона в Афинах, месте, предназначенном только для состоятельных людей. Математическое образование он получил от учеников Платона.

Продолжить чтение ниже

Карьера

«Элементы» Евклида считается одной из самых влиятельных работ в истории математики с момента ее публикации до конца 19 или начала 20 века. Он фактически служил основным учебником для преподавания математики в этот период.

В своих «Элементах» он вывел принципы «евклидовой геометрии» из небольшого набора аксиом. Евклид также написал работы по перспективе, коническим сечениям, сферической геометрии, теории чисел и строгости.

Помимо самого известного его произведения «Элементы», до наших дней дошло не менее пяти произведений Евклида. Кажется, что они следуют той же логической структуре, что и в «Элементах». Это «Данные», «О делении фигур», «Катоптрика», «Феномен» и «Оптика».

В дополнение к вышеупомянутым работам есть несколько других работ, которые приписываются Евклиду, но были утеряны. К таким работам относятся «Коники», «Псевдарии», «Поризмы», «Поверхностные локусы» и «О тяжелом и легком».

Элементы Евклида

«Элементы» — математический и геометрический трактат, состоящий из 13 книг, написанных этим великим древнегреческим математиком в Александрии, Птолемеевском Египте ок. 300 г. до н.э.

«Начала» Евклида — это собрание определений, постулатов, теорем и построений, а также математических доказательств предложений. Все 13 книг охватывают евклидову геометрию и древнегреческую элементарную теорию чисел.

Он также включает в себя геометрическую алгебру, которая помогает в решении многих алгебраических задач, включая задачу нахождения квадратного корня из числа.

«Начала» — второй из старейших греческих математических трактатов после «О движущейся сфере» Автолика, который сыграл важную роль в развитии логики и современной науки.

Продолжить чтение ниже

Впервые напечатанная в 1482 году в Венеции, «Элементы» — одна из самых ранних математических работ, напечатанных после изобретения печатного станка.

Он считается самым успешным и влиятельным учебником из когда-либо написанных, а по количеству выпущенных изданий уступает только Библии. Говорят, что с момента появления книгопечатания было выпущено более 1000 изданий «Элементов».

Другие работы

«Элементы» были самой известной работой Евклида и продолжают оказывать влияние на математику даже по сей день, но он также написал ряд других книг. До наших дней дошло не менее 5 произведений Евклида.

Данные: Эта книга содержит 94 предложения и в основном посвящена природе и значениям «данной» информации в геометрических задачах.

О делениях фигур: Еще одна важная работа Евклида, но сохранившаяся лишь частично в арабском переводе. Это напоминает работу (3 век) «Герона Александрийского»

Катоптрика: Это еще одна важная работа, связанная с математической теорией зеркал. Однако Дж. Дж. О’Коннор и Э. Ф. Робертсон считают настоящим автором «Теона Александрийского».

Феномены: проливает свет на сферическую астрономию. Он поразительно похож на «О движущейся сфере» Автолика из Питана, творившего около 310 г. до н.э.

Оптика: Эта работа делится знаниями о теории перспективы и является самым ранним сохранившимся греческим трактатом о перспективе.

Помимо пяти вышеупомянутых сохранившихся работ, есть еще несколько работ, приписываемых Евклиду, но утерянных. Это «Коники», «Поризмы», «Псевдарии» и «Поверхностные локусы». Кроме того, различные арабские источники считают Евклида автором ряда работ по механике.

Продолжить чтение ниже

Личная жизнь и наследие

Существует не так много информации и записей, касающихся личной жизни Евклида, но историки считают, что он умер около 260 г. до н.э.

Его самая известная книга «Элемент» была в конечном итоге переведена с арабского на латынь Кампанусом. Первое печатное дополнение появилось в 1482 году в Венеции.

В 1570 году Джон Ди перевел «Элемент» на английский язык. Лекции Ди смогли возродить интерес к математике в Англии.

Итальянский математик Джироламо Саккери в 1733 году много лет пытался превзойти работы Евклида, но его попытки опровергнуть их оказались тщетными, так как он не смог найти ни единого изъяна в теориях Евклида. В конце концов, он сдался и опубликовал книгу «Евклид очищен от всех недостатков».

Наследие, оставленное Евклидом, огромно. Он вдохновлял таких личностей, как Авраам Линкольн, который всегда религиозно носил с собой «Элементы» и цитировал гения в своих речах.

Евклид оказал влияние на великих философов и математиков, таких как Ньютон и Декарт, которые изложили свои философские работы, используя формат и структуру Элюцида. Они также перешли от простых принципов к сложным концепциям, как Elucid.

10 главных фактов о Евклиде, которых вы не знали

Имя «Евклид» означает «известный, славный». примерно в начале 20 века

Большинство других греческих математиков, начиная с Архимеда, называли его «автором Элементов», а не по имени.

Некоторые исследователи считают, что Евклид не был историческим персонажем и что его работы были написаны группой математиков, которые все вместе взяли имя Евклид. Однако доказательств, подтверждающих эту гипотезу, немного.

Оптика Евклида была первой сохранившейся греческой диссертацией по проблематике оптики.

Его работа «Разделения фигур» сохранилась лишь частично в арабском переводе.

Подробную биографию Евклида дали арабские авторы, однако исследователи считают этот труд полностью вымышленным.

Средневековые переводчики и редакторы часто путали Евклида с философом Евклидом из Мегары, жившим примерно столетием раньше.

Геометрическая система, которую он описал в «Элементах», называется евклидовой геометрией, чтобы отличить ее от других так называемых неевклидовых геометрий, открытых математиками в 19 веке.

Часто говорят, что «Элементы» — одна из самых переводимых, издаваемых и изучаемых книг из всех книг, выпущенных в западном мире.

Евклид — Энциклопедия Нового Света

Евклид , изображенный Юстусом ван Гентом, ок. Пятнадцатый век; не сохранилось ни сходства, ни описания внешности Евклида, сделанного при его жизни.0128 — ок. 265 г. до н. э. ), греческий математик, живший в Александрии, эллинистическом Египте, почти наверняка во времена правления Птолемея I (323 г. до н. э. – 283 г. до н. э. ), часто упоминается как «отец геометрии». Его самая популярная работа « Элементы » считается одним из самых успешных учебников в истории математики. В нем свойства геометрических объектов выводятся из небольшого набора аксиом, устанавливая аксиоматический метод математики. Таким образом, Евклид навязал логическую организацию известным математическим истинам посредством дисциплинированного использования логики. Более поздние философы адаптировали эту методологию в своих областях.

Хотя книга Elements наиболее известна своим изложением геометрии, она также включает различные результаты по теории чисел, такие как связь между совершенными числами и простыми числами Мерсенна, доказательство бесконечности простых чисел, лемму Евклида о факторизации (которая приводят к фундаментальной теореме арифметики об уникальности простых факторизаций) и алгоритму Евклида для нахождения наибольшего общего делителя двух чисел. Элементы были опубликованы примерно в тысяче изданий и использовались западным миром в качестве основного текста по геометрии в течение двух тысяч лет.

Содержимое

• 1 срок службы
• 2 Работы
• 3 Элементы
  • 3. 1 История
  • 3.2 Схема элементов
  • 3.3 Основные принципы
  • 3.4 Постулат Параллели
  • 3.5 Содержание тринадцати книг
  • 3.6 Критика
• 4 Примечания
• 5 См. также
• 6 Каталожные номера
• 7 Внешние ссылки
  • 7.1 Общие философские источники
• 8 кредитов

Евклид также написал работы по перспективе, коническим сечениям, сферической геометрии и, возможно, квадратичным поверхностям. Не установлены ни год, ни место его рождения, ни обстоятельства его смерти.

Жизнь

Мало что известно о Евклиде, кроме того, что представлено в Элементах и других его сохранившихся книгах. То небольшое количество биографической информации, которое у нас есть, в основном получено из комментариев Прокла и Паппа Александрийских: Евклид работал в великой Александрийской библиотеке и, возможно, учился в Академии Платона в Греции. Точная продолжительность жизни и место рождения Евклида неизвестны. Некоторые писатели Средневековья ошибочно путали его с Евклидом Мегарским, греческим философом-сократиком, жившим примерно столетием раньше.

Works

Фронтиспис первой английской версии книги сэра Генри Биллингсли « Элементы» Евклида , 1570

Самая известная работа Евклида « Элементы, » считается одним из самых успешных учебников в истории математики. В нем свойства геометрических объектов выводятся из небольшого набора аксиом, устанавливая аксиоматический метод математики.

Помимо Элементов , до наших дней сохранились пять произведений Евклида.

• Данные имеют дело с природой и значением «данной» информации в геометрических задачах; предмет тесно связан с первыми четырьмя книгами Элементов .
• О делении фигур , который сохранился лишь частично в арабском переводе, касается деления геометрических фигур на две или более равные части или на части в заданных соотношениях. Он похож на работу Герона Александрийского г. н.э. третьего века, за исключением того, что в работе Евклида характерно отсутствие каких-либо численных расчетов.
• Явления касается применения сферической геометрии к задачам астрономии.
• Оптика , самый ранний сохранившийся греческий трактат о перспективе, содержит положения о видимых размерах и формах объектов, рассматриваемых с разных расстояний и под разными углами.
• Катоптрика , которая касается математической теории зеркал, в частности изображений, сформированных в плоских и сферических вогнутых зеркалах.

Все эти работы следуют основной логической структуре Элементы , содержащие определения и доказанные предложения.

Есть четыре работы, достоверно приписываемые Евклиду, которые были утеряны.

• Conics был работой по коническим сечениям, которая позже была расширена Аполлонием Пергским в его знаменитую работу на эту тему.
• Поризмы могли быть результатом работы Евклида с коническими сечениями, но точное значение названия вызывает споры.
• Псевдария или Book of Fallacies — элементарный текст об ошибках в рассуждениях.
• Поверхностные локусы касались либо локусов (наборов точек) на поверхностях, либо локусов, которые сами были поверхностями; в соответствии с последней интерпретацией было высказано предположение, что работа могла иметь дело с квадратичными поверхностями.

Элементы

Элементы Евклида (греч. Στοιχεῖα) — математический и геометрический трактат, состоящий из тринадцати книг, написанный около 300 г. г. до н. э. Содержит собрание определений, постулатов (аксиом), утверждений (теорем и конструкций) и доказательств теорем. Тринадцать книг охватывают евклидову геометрию и древнегреческую версию элементарной теории чисел. Elements — это старейшая из сохранившихся аксиоматических дедуктивных трактовок математики, которая сыграла важную роль в развитии логики и современной науки.

« Элементы » Евклида — самый успешный учебник из когда-либо написанных. Это была одна из самых первых работ, напечатанных после изобретения печатного станка, и уступает только Библии по количеству опубликованных изданий (более тысячи). Он использовался в качестве основного текста по геометрии во всем западном мире около двух тысяч лет. На протяжении столетий, когда квадривиум был включен в учебную программу всех студентов университетов, знание хотя бы части евклидова Elements требовался от всех учащихся. Только в двадцатом веке она перестала считаться тем, что читали все образованные люди.

Геометрическая система, описанная в Elements , долгое время была известна просто как «геометрия». Однако сегодня ее часто называют евклидовой геометрией, чтобы отличить ее от других так называемых неевклидовых геометрий, открытых в девятнадцатом веке. Эти новые геометрии возникли в результате более чем двухтысячелетнего исследования пятого постулата Евклида (постулата о параллельности), одной из наиболее изученных аксиом во всей математике. Большинство этих исследований включало попытки доказать относительно сложный и предположительно неинтуитивный пятый постулат, используя остальные четыре (подвиг, который в случае успеха показал бы, что постулат на самом деле является теоремой).

История

Женщина, преподающая геометрию , иллюстрация в начале средневекового перевода Евклида « Элементы » (ок. 1310)

некоторые оригинальные работы Евклида. Текст Евклида содержит некоторые недостающие доказательства и включает разделы по теории чисел и трехмерной геометрии. Знаменитое доказательство Евклида бесконечности простых чисел находится в книге IX, предложение 20.

Прокл, греческий математик, живший через несколько столетий после Евклида, пишет в своем комментарии к « Элементам »: «Евклид, сложивший воедино Элементов , собрав многие теоремы Евдокса, усовершенствовав многие теоремы Теэтета, а также доведя до неопровержимая демонстрация того, что было лишь несколько приблизительно доказано его предшественниками».

Версия ученика Евклида по имени Прокло была позже переведена на арабский язык после того, как была получена арабами из Византии и из тех вторичных переводов на латынь. Первое печатное издание появилось в 1482 году (на основе издания Джованни Кампано 1260 года), и с тех пор оно было переведено на многие языки и опубликовано примерно в тысяче различных изданий. В 1570 году Джон Ди представил широко уважаемое «Математическое предисловие» вместе с обильными примечаниями и дополнительными материалами к первому английскому изданию Генри Биллингсли.

Копии греческого текста также существуют в Ватиканской библиотеке и Бодлеанской библиотеке в Оксфорде. Однако доступные рукописи очень разного качества и неизменно неполные. Путем тщательного анализа переводов и оригиналов были выдвинуты гипотезы о содержании оригинального текста (копии которого больше не доступны).

Древние тексты, которые относятся к Элементам и другим математическим теориям, которые были актуальны на момент его написания, также важны в этом процессе. Такой анализ проведен Дж. Л. Хейбергом и сэром Томасом Литтлом Хитом в их изданиях Элементы .

Также важны схолии или аннотации к тексту. Эти дополнения, которые часто отличались от основного текста (в зависимости от рукописи), постепенно накапливались с течением времени, поскольку мнения менялись относительно того, что заслуживает объяснения или разъяснения.

Схема

Элементов

Доказательство из Элементов Евклида того, что для данного отрезка существует равносторонний треугольник, который включает отрезок в качестве одной из своих сторон. Доказательство построено: равносторонний треугольник АВГ получается из окружностей А и Е с центрами в точках А и В и взятия одной точки пересечения окружностей за третью вершину треугольника.

Элементы до сих пор считаются шедевром в применении логики к математике, и, исторически, его влияние во многих областях науки невозможно переоценить. Ученые Николай Коперник, Иоганн Кеплер, Галилео Галилей и особенно сэр Исаак Ньютон применяли знания о Элементах в своей работе. Математики (Бертран Рассел, Альфред Норт Уайтхед) и философы, такие как Барух Спиноза, также пытались использовать метод аксиоматизированных дедуктивных структур Евклида для создания основ своих собственных дисциплин. Даже сегодня во вводных учебниках по математике часто встречается слово 9.0135 элементов в названиях.

Успех Элементов обусловлен, прежде всего, логическим изложением большей части математических знаний, доступных Евклиду. Большая часть материала ему не принадлежит, хотя многие доказательства принадлежат ему. Тем не менее, систематическое развитие Евклидом своего предмета, от небольшого набора аксиом до глубоких результатов, и последовательность его подхода во всех « элементах» поощряли его использование в качестве учебника в течение примерно двух тысяч лет. Элементы до сих пор влияют на современные книги по геометрии. Кроме того, ее логический аксиоматический подход и строгие доказательства остаются краеугольным камнем математики.

Хотя Элементы в первую очередь геометрическая работа, она также включает результаты, которые сегодня были бы классифицированы как теория чисел. Евклид, вероятно, решил описать результаты теории чисел в терминах геометрии, потому что он не мог разработать конструктивный подход к арифметике. Конструкция, используемая в любом из доказательств Евклида, требовала доказательства того, что она действительно возможна. Это позволяет избежать проблем, с которыми столкнулись пифагорейцы с иррациональными числами, поскольку их ложные доказательства обычно требовали такого утверждения, как «9».0135 Найдите наибольшую общую меру … » ^[1]

Первые принципы

Книга 1 Евклида начинается с 23 определений, таких как точка , линия и поверхность , за которыми следуют пять постулатов и пять «общих понятий» (оба из которых сегодня называются аксиомами) — основа всего последующего.

Постулаты:

1. Отрезок прямой линии можно построить, соединив любые две точки.
2. Отрезок прямой линии можно бесконечно удлинять по прямой.
3. Имея отрезок прямой линии, можно нарисовать окружность, используя отрезок в качестве радиуса и одну конечную точку в качестве центра.
4. Все прямые углы равны.
5. Если провести две прямые, пересекающие третью таким образом, что сумма внутренних углов с одной стороны меньше двух прямых, то две прямые неизбежно должны пересечь друг друга с этой стороны, если их продолжить достаточно далеко.

Общие понятия:

1. Вещи, равные одной и той же вещи, равны друг другу (переходное свойство равенства).
2. Если равные прибавляются к равным, то суммы равны.
3. Если из равных вычесть равные, то остатки равны.
4. Вещи, которые совпадают друг с другом, равны друг другу. (Рефлексивное свойство равенства)
5. Целое больше части.

Эти основные принципы отражают интерес Евклида и современных ему греческих и эллинистических математиков к конструктивной геометрии. Первые три постулата в основном описывают построения, которые можно выполнять с помощью циркуля и линейки без опознавательных знаков. Размеченная линейка, используемая в построении neusis, запрещена в евклидовом построении, вероятно, потому, что Евклид не смог доказать, что пересекающиеся линии пересекаются.

Постулат о параллельности

Если сумма двух внутренних углов равна 180°, прямые параллельны и никогда не пересекутся

Последний из пяти постулатов Евклида заслуживает особого упоминания. Так называемый постулат параллельности всегда казался менее очевидным, чем другие. Сам Евклид использовал его очень экономно в остальной части Elements . Многие геометры подозревали, что это можно доказать из других постулатов, но все попытки сделать это потерпели неудачу.

К середине девятнадцатого века было показано, что такого доказательства не существует, потому что можно построить неевклидову геометрию, где постулат параллельности ложен, а другие постулаты остаются верными. По этой причине математики говорят, что постулат параллельности не зависит от других постулатов.

Две альтернативы постулату параллельности возможны в неевклидовой геометрии: либо бесконечное число параллельных линий может быть проведено через точку не на прямой линии в гиперболической геометрии (также называемой геометрия Лобачевского ), или никто не может в эллиптической геометрии (также называемой римановой геометрией ). То, что другие геометрии могут быть логически непротиворечивыми, было одним из самых важных открытий в математике, имевшим огромное значение для науки и философии. Действительно, общая теория относительности Альберта Эйнштейна показывает, что «реальное» пространство, в котором мы живем, может быть неевклидовым (например, вокруг черных дыр и нейтронных звезд).

Содержание тринадцати книг

Книги с 1 по 4 посвящены планиметрии:

• Книга 1 содержит основные свойства геометрии: теорему Пифагора, равенство углов и площадей, параллелизм, сумму углов в треугольнике и три случая, когда треугольники «равны» (имеют одинаковую площадь) .
• Книгу 2 обычно называют «книгой по геометрической алгебре», потому что содержащийся в ней материал легко интерпретируется в терминах алгебры.
• Книга 3 посвящена окружностям и их свойствам: вписанным углам, касательным, силе точки.
• Книга 4 посвящена описанию и описанию треугольников и правильных многоугольников.

Книги с 5 по 10 знакомят с соотношениями и пропорциями:

• Книга 5 представляет собой трактат о пропорциях величин.
• Книга 6 применяет пропорции к геометрии: теорема Фалеса, подобные фигуры.
• Книга 7 строго посвящена элементарной теории чисел: делимость, простые числа, наибольший общий делитель, наименьшее общее кратное.
• Книга 8 посвящена пропорциям в теории чисел и геометрическим последовательностям.
• Книга 9 применяет результаты предыдущих двух книг: бесконечность простых чисел, сумма геометрического ряда, совершенные числа.
• Книга 10 пытается классифицировать несоизмеримые (на современном языке, иррациональные) величины, используя метод исчерпывания, предшествующий интегрированию.

Книги с 11 по 13 посвящены пространственной геометрии:

• Книга 11 обобщает результаты Книг 1–6 на пространство: перпендикулярность, параллельность, объемы параллелепипедов.
• Книга 12 вычисляет площади и объемы, используя метод исчерпывания: конусы, пирамиды, цилиндры и сферы.
• Книга 13 обобщает Книгу 4 на пространство: золотое сечение, пять правильных (или Платоновых) тел, вписанных в сферу.

Критика

Несмотря на всеобщее признание и успех, Elements подверглась серьезной критике, большая часть которой была оправдана. Постулат Евклида о параллельности, рассмотренный выше, был главной целью критиков.

Другая критика заключается в том, что определений недостаточно для полного описания определяемых терминов. В первой конструкции Книги 1 Евклид использовал посылку, которая не была ни постулирована, ни доказана: две окружности с центрами на расстоянии их радиуса пересекаются в двух точках (см. иллюстрацию выше). Позже, в четвертой конструкции, он использовал движение треугольников, чтобы доказать, что если две стороны и их углы равны, то они конгруэнтны; однако он не постулировал и даже не определял движение.

В девятнадцатом веке элементов подверглись еще большей критике, когда постулаты оказались одновременно неполными и излишними. В то же время неевклидовы геометрии привлекли внимание современных математиков. Ведущие математики, включая Ричарда Дедекинда и Дэвида Гильберта, пытались добавить аксиомы к элементам , такие как аксиома непрерывности и аксиома конгруэнтности, чтобы сделать евклидову геометрию более полной.

Математик и историк В. В. Роуз Болл рассмотрел критику в перспективе, отметив, что «тот факт, что в течение двух тысяч лет [ Элементы ] был обычным учебником по этому предмету, что вызывает серьезное предположение, что он не является непригодным для этой цели». Проблемы теории чисел . Американское математическое общество

↑ В. В. Роуз Болл (1960). Краткий обзор истории математики , 4-е изд. (Оригинальная публикация: Лондон: Macmillan & Co., 1908 г.), Минеола, Нью-Йорк: Dover Publications, 55. ISBN 0486206300.

См. также

• Геометрия

Ссылки

Ссылки ISBN поддерживают NWE за счет реферальных сборов

• Artmann, Benno. (1999). Евклид: создание математики . Нью-Йорк: Спрингер. ISBN 0387984232.
• Болл, В. В. Роуз. (1908). Краткий обзор истории математики , 4-е изд. Нью-Йорк: Dover Publications, 1960. стр. 50–62 ISBN 0486206300
• Балмер-Томас, Айвор. (1971). «Евклид». Научно-биографический словарь.
• Хит, Томас Л. Тринадцать книг Элементов Евклида , 3 тома. Нью-Йорк: Dover Publications, 1956. ISBN 0486600882 (том 1), ISBN 0486600890 (том 2), ISBN 0486600904 (том 3)
• Хит, Томас Л. (1981). История греческой математики , 2 тома. Нью-Йорк: Dover Publications. ISBN 0486240738, ISBN 0486240746
• Клайн, Моррис (1980). Математика: потеря достоверности . Оксфорд: Издательство Оксфордского университета. ISBN 019502754X

Внешние ссылки

Все ссылки получены 13 августа 2017 г.

• Евклид — Биография MacTutor
• Аристотель и математика, Стэнфордская философская энциклопедия
• Элементы Евклида — все тринадцать книг с интерактивными диаграммами с использованием Java — Университет Кларка
• Euclides. org – все тринадцать книг на испанском и каталанском языках
• Издание Оливера Бирна 1847 года — необычная версия с использованием цвета, а не меток, таких как ABC (отсканированные изображения страниц, общественное достояние) — математический факультет Университета Британской Колумбии
• Чтение Евклида – Университет Денвера
• Английский перевод Хита – Университет Тафтса

Общие источники по философии

• Стэнфордская философская энциклопедия
• Интернет-энциклопедия философии
• Проект Пайдейя Онлайн
• Проект Гутенберг

Авторы

Энциклопедия Нового Света авторов и редакторов переписали и дополнили статью Википедии в соответствии с Энциклопедия Нового Света стандартов. Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа.